混凝土凝结收缩对板拱桥拱脚开裂影响分析

梅盖伟，张肄，侯国虎，李强

（中机中联工程有限公司，重庆 400074）

0 引言

拱桥具有特殊的拱形构造，可将全桥荷载完美转化为拱轴向压力，充分利用混凝土抗压性能优异的特点，极大地提升跨越能力[1]。钢筋混凝土板拱桥作为中、小跨径拱桥的代表，构造简单、施工便捷，同时，其能极好地将经济与美观相结合，深受桥梁设计师的青睐。钢筋混凝土板拱桥主拱圈截面为矩形，常采用搭设满堂支架现浇的施工方法，该法稳定性好，较为经济合理[2]。

收缩是混凝土在空气中凝结硬化的固有特性，其收缩应变常由三部分构成：一是水泥水化反应产生的自生收缩应变；二是混凝土内部失水产生的干缩应变；三是水泥水化物与空气中CO2反应产生的碳化收缩应变[3-4]。鉴于混凝土具有凝结收缩的特性，采用满堂支架现浇法施工时，由于墩台及模板的约束，其分条浇筑宽度及分段浇筑长度的差异，会导致主拱圈拱脚位置不同程度内力的产生。混凝土抗压性能优良，但当其体内出现拉应力时，极易被拉裂[5-6]。对于承重型混凝土结构，产生裂缝可能会降低结构的承载能力和使用寿命。

为追求浇筑效率，我国钢筋混凝土板拱桥施工常采用整幅混凝土同时浇筑的方式，这将导致采用此工法修建的钢筋混凝土板拱桥在拱脚区段出现斜向开裂。本文对钢筋混凝土板拱桥拱脚位置斜向裂缝成因及规避方法进行了探讨。

1 工程概况及裂缝成因

依托工程为全长100m、三跨钢筋混凝土空腹上承式连续拱桥。其中，两边跨主拱净跨径20m，计算跨径20.3448m，矢跨比1/5，拱轴线为圆弧线；中跨主拱净跨径40m，计算跨径40.4261m，矢跨比3/20，拱轴线为悬链线，拱轴系数1.6086。该桥边跨主拱圈采用宽16m、高0.5m矩形截面；中跨主拱圈采用宽16m、高0.8m矩形截面。主拱圈采用C50混凝土浇筑，纵向分5段满堂支架现浇，在主拱圈上浇筑横墙，并于横墙上现浇腹拱圈，实现对拱上填料及桥面板支撑。拱桥立面布置图见图1。

图1 某拱桥立面布置图

由于中跨主拱圈矢跨比较边跨小，浇筑养护期间，其自重沿拱圈径向分力大，模板与混凝土间摩擦力大，模板约束效应更为显著。同时，其截面高度较边跨大，墩台对主拱现浇混凝土的约束更明显。因此，本文研究中跨主拱圈在凝结收缩作用下的力学行为。

对于多跨连续钢筋混凝土板拱桥，常于跨度方向分多段浇筑，较少于宽度方向分多条带浇筑。该工程拱座施工完成后，间隔30天浇筑主拱混凝土。主拱混凝土浇筑并养护完成后，拆模时在拱脚附近发现斜裂缝，部分裂缝贯穿（图2），虽在后续施工过程中，该裂缝并未增大或扩展，但仍对拱桥结构受力产生了不利影响。在此施工过程中，由于主拱圈混凝土凝结收缩，加之其与墩台存在龄期差，形成墩台对其收缩徐变约束，在拱脚产生横桥向拉应力[7]。同时，底模的约束使拱脚段混凝土受到纵桥向拉应力，二者合力垂直于裂缝开展方向，如图3所示。

图2 裂缝开展图

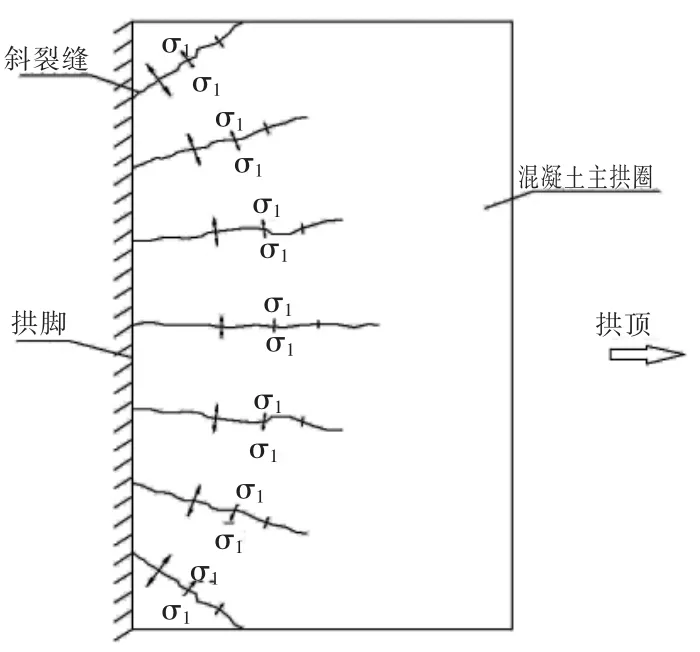
图3 合力分布图

2 计算模式

针对混凝土收缩应变，常采用有限元方法建模分析[8-9]，本次采用工程实体有限元软件Midas/FEA软件辅助建模。混凝土收缩变形较小，假定混凝土为各向同性弹性体，当各向同性弹性体收缩时，收缩中心为其形心。拱脚端采用固结约束，模板与混凝土间摩擦力相对复杂，本文将该边界条件简化为混凝土板中央限制轴向位移，摩擦因素仅受到模板表面粗糙系数的影响。

由于其他段混凝土及拱上建筑施工时，拱脚段混凝土受力复杂，为简化计算，本文仅分析第一段混凝土浇筑及养护期间的收缩现象。

混凝土收缩应变影响因素复杂，主要包含自身材料、构件尺寸及环境湿度等的影响，因此，难以进行精确的理论计算，各国规范对此估算也有不同规定[10-11]。本文采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》中规定的混凝土收缩应变公式进行计算：

式中：t为计算考虑时刻的混凝土龄期（d）；ts为收缩开始时的混凝土龄期（d）；εcs(t,ts)为计算考虑的龄期为t时的收缩应变；εcso为名义收缩系数；βs为收缩随时间发展的系数；fcm为强度等级C25～C50混凝土在28d龄期时的平均圆柱体抗压强度（MPa）；βRH为与年平均相对湿度相关的系数；RH为环境年平均相对湿度；βsc为水泥种类系数；h为构件理论厚度。

将该工程参数代入公式（1）—（5），可绘出时间-收缩应变曲线，如图4所示。

图4 时间-收缩应变曲线

混凝土收缩裂缝产生的原因为抗拉强度小于其受到的收缩应力，提高抗拉强度往往需要埋入钢筋、提高混凝土标号，而收缩应力主要受养护条件和边界约束的影响。加强养护可大幅减小收缩应变，从而减小混凝土受到的收缩应力，同时过强的约束也是造成混凝土收缩开裂的直接原因。

建立有限元模型，如图5所示。

图5 精细化有限元模型

从图6中可看出，由于混凝土具有收缩徐变性质，在28天养护后，最大收缩量达到0.116mm。

图6 混凝土板收缩应变

3 裂缝影响因素及削弱方式

3.1 纵向分段对拱脚应力的影响

为对比分析主拱圈纵向分段浇筑长度对拱脚应力的影响，沿主拱纵向将浇筑长度定为10m，依次渐变至5m，按标准养护28天计算，然后建模分析，得出结果见图7。

图7 混凝土分段浇筑长度-第一主应力图

对上述结果进行分析可知，混凝土板第一主应力随分段长度减小而减小，但其变化不明显，可见主拱圈混凝土分段浇筑长度对拱脚所受第一主应力影响较小。由于纵向模板对混凝土的约束相对拱脚端而言，强度较弱，且考虑其一端为自由端，与之对应的约束反力较小，当仅改变纵向分段长度时，对应力结果影响不明显。因此，综合考虑施工单位混凝土浇筑能力及工程经济性，本文仅讨论沿主拱轴向一次性浇筑10m长度混凝土板所受的第一主应力。

3.2 横向分条对拱脚应力的影响

为对比分析主拱圈横向分条浇筑宽度对拱脚应力的影响，将分条宽度沿主拱横向分别定为16m，依次渐变至6m，然后建模分析，得出结果如图8—图13所示。

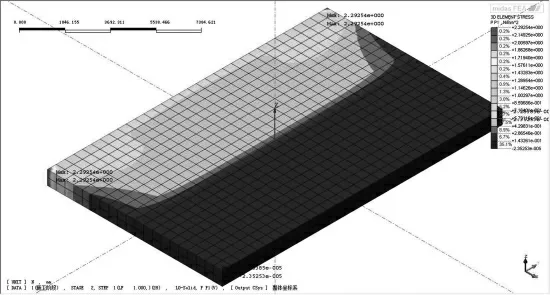
图8 16m宽混凝土板第一主应力

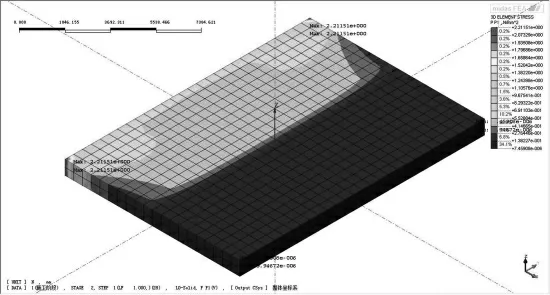
图9 14m宽混凝土板第一主应力

图10 12m宽混凝土板第一主应力

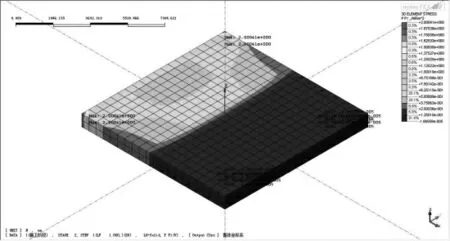
图11 10m宽混凝土板第一主应力

图12 8m宽混凝土板第一主应力

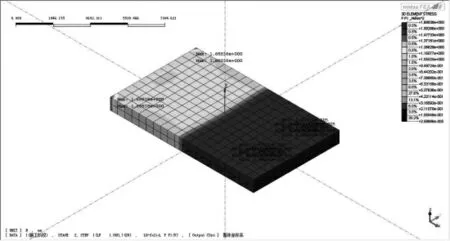
图13 6m宽混凝土板第一主应力

将以上结果进行分析，得出混凝土分条浇筑宽度-第一主应力图，如图14所示。

图14 混凝土分条浇筑宽度-第一主应力图

由图14可得，混凝土板第一主应力与其分条长度正相关。混凝土为各向同性体，当其凝结收缩时，各个位置应变保持一致，但靠近拱脚角点处的收缩位移随板宽的增大而增大，该位置处的约束力也随之增大。由于主拱板厚并未改变，角点受力截面也不变，导致其第一主应力随分条浇筑宽度增加而增大。根据文献[11]，得到C50混凝土容许拉应力为1.83MPa。

应用最小二乘法对混凝土分条浇筑宽度与第一主应力关系进行拟合。设目标函数为二次多项式：

将残差平方和作为拟合误差，可表示为：

为使拟合误差最小，将上式求偏导，并令导数为0：

代入各分布点坐标，利用科学计算软件MATLAB可求得拟合函数为：

将上式系数代入式（7），可得残差平方和：

决定系数可由下式计算：

由式（12）可以得出，拟合函数的决定系数R2可达0.999771，该函数与模型计算值的相关程度极高。

将C50混凝土容许拉应力1.83MPa代入式（9），可得混凝土分条浇筑最大宽度为7.66m，即分条浇筑宽度须控制在7.66m以下，主拱圈混凝土才不至于因凝结收缩而开裂破坏。

4 结语

本文结合某钢筋混凝土板拱桥拱脚开裂现象，利用有限元软件Midas/FEA对拱脚附近混凝土拱圈进行实体建模分析，以研究拱脚斜向裂缝成因及规避方案，主要得出以下结论：

（1）拱脚附近斜裂缝成因为：主拱圈混凝土与墩台存在龄期差，收缩不同步，加之底模的约束，导致主拱圈混凝土浇筑后的凝结收缩受限，第一主应力超出其容许拉应力；

（2）对比分析主拱圈混凝土分段浇筑长度与分条浇筑宽度对其第一主应力的影响，发现混凝土凝结收缩应力对主拱圈的分条浇筑宽度更为敏感；

（3）根据主拱圈混凝土在不同分条浇筑宽度条件下于拱脚处产生的拉应力，拟出了分条宽度与第一主应力关系式，考虑C50混凝土容许拉应力，得出最大分条宽度为7.66m。