A new path planning method for bevel-tip flexible needle insertion in 3D space with multiple targets and obstacles

Zhen Tan·Dan Zhang·Hua-geng Liang·Qing-guo Wang·Wenjian Cai

Received:2 May 2022/Revised:19 June 2022/Accepted:28 June 2022/Published online:17 October 2022

©The Author(s),under exclusive licence to South China University of Technology and Academy of Mathematics and Systems Science,Chinese Academy of Sciences 2022

Abstract In this paper, a new bevel-tip flexible needle path planning method based on the bee-foraging learning particle swarm optimization (BFL-PSO) algorithm and the needle retraction strategy in 3D space is proposed to improve the puncture accuracy and shorten the puncture distance in the case of multiple puncture targets.First,the movement of the needle after penetrating the human body is analyzed,and the objective function which includes puncture path error,puncture path length,and collision function is established.Then,the BFL-PSO algorithm and the needle retraction strategy are analyzed.Finally,medical images of the tissue to be punctured are obtained by medical imaging instruments,i.e.,magnetic resonance(MR),and the 3D model of the punctured environment is constructed by 3D Slicer to obtain the environment information on targets and obstacles, and the path of flexible needle is carried out based on the BFL-PSO optimization algorithm and the needle retraction strategy. The simulation results show that, compared with other path planning methods in the related literature,the new path planning method proposed in this paper has higher path planning accuracy,shorter puncture distance,and good adaptability to multi-target path planning problems.

Keywords Path planning·Multi-objective optimization·Bee-foraging learning·Particle swarm

1 Introduction

In modern clinical practice, percutaneous puncture surgery has been found applications in preoperative tissue biopsy,local anesthesia, and other clinic operations [1,2].The percutaneous interventional diagnosis has been widely used because of its advantages such as less surgical trauma and quick postoperative recovery. Traditional puncture surgery needs doctors to carry out the operation with a hand-held puncture device assisted by CT or ultrasound instruments,and doctors would thus be exposed to radiation directly[3].In addition,traditional puncture needles have high hardness,and the puncture path is similar to straight line. The direction of the tip can only be adjusted by controlling the needle seat, which not only leads more pains to patients but also causes unnecessary harm to human tissue. Moreover, the puncture accuracy required for organs such as the kidney,prostate, or liver is relatively high [4]. For inexperienced doctors, hand-held puncture surgery under the guidance of images is a big challenge, and the success rate of puncture operation is low[5].It is also easy to lead to fatigue of doctors,whichaffects theaccuracyof surgical operations greatly.If there are multiple lesions or target points in the tissues,the puncture needle should be completely pulled out of the tissue for each unreached target and then puncture for the next target. On the one hand, this operation will increase the length of the puncture path, and on the other hand, the puncture needle will destroy more human tissues, causing more pain to patients, and the postoperative recovery time will also be longer.Therefore,how to successfully design a high-precision puncture path planning method for multiple targets in 3D space is particularly important.

Webster et al. designed a new type of flexible needle to improve the controllability of the puncture operation [6].When the needle tip penetrates into the human tissue, the inclined surface of the needle will be subjected to the pressure exerted by the tissue.The asymmetric force acting on the needle tip will change the trajectory of the needle tip.If there are obstacles in the puncture environment,the flexible needle can circumvent the obstacles flexibly and avoid unnecessary damage to human tissues.Thus,a good flexible needle model is the basis for effective path planning.Using nonholonomic constraints,Webster et al.proposed the unicycle model and bicycle model based on the Lie group theory[6].Based on the bicycle model proposed by Webster et al.,Zhao et al.proposed a more perfect bicycle model with return trip,and then,a two-dimensional path optimization algorithm combining with multiple path forms and a needle–tissue interaction model considering the nonlinear and anisotropy of soft tissue were established;see more details in[7–9].Some other interesting results were also reported in the literature. For example, Glozman et al. established a viscoelastic model using virtual springs and linear beams[10].Abolhassani et al.regarded the needle as a cantilever beam to calculate the bending of the needle[11].Zheng et al.further divided the cantilever beam into multiple sections to calculate the deformation of the needle[12].In addition,several methods have been proposed to assist needle positioning and insertion[13–15].

Note that the quality of the path planning method has a great influence on whether the needle tip can reach the target point accurately. Dimaio et al. used the finite-element method to simulate the tissue deformation and used the artificial potential field method to plan the flexible needle path[16]. By defining the potential energy field function, Jiang et al.established a three-dimensional comprehensive potential energy field to plan the trajectory of flexible needle[17].Although the artificial potential field method is simple to calculate,it is easy to fall into local optimum,especially when there are multiple obstacles in the puncture environment,the shortcoming is more obvious. Moreover, the finite-element method has a large amount of computation and it is prone to the curse of dimensionality. Alterovitz et al. proposed a Dubins car model based on nonholonomic constraints and defined the “cost” of path error, path length, path collision with obstacles,and needle tip rotation,and then,the Markov decision process(MDP)was used to establish motion planning equations to calculate the puncture control sequence based on the infinite norm dynamic programming strategy[18].Abayazid et al.proposed a method based on accessibility and RRT algorithm [19], where the RRT algorithm was used to generate the milestones, and then, the accessibility was used to calculate the position of the next point.However,the path planned by this method is often not optimal.Huo et al.used the colorless Kalman filter to estimate the tip position of the needle and planned the puncture path through the accessibility method, the simulation showed that the puncture simulation error is below 0.5mm[20].In[21],Chen et al. designed an ultrasound-assisted puncture path planning system, which was applied to the ultrasound-guided robot system.

In recent years, many heuristic optimization algorithms have also been used to deal with the path planning problem.Huo et al. established the puncture optimization objective function and solved the puncture path with the particle swarm optimization algorithm. The puncture simulation error was controlled below 0.1mm by this method[22].Tan et al.used the universal distributional Q-learning algorithm to learn the stable steering strategy and plan the feasible path of the flexible puncture needle[23].Segato et al.obtained 2D and 3D environments from magnetic resonance (MR) images and used the GA3C algorithm to create a model to plan the flexible needle puncture path[24].Although these path planning methods have achieved great path planning results,there still leaves some further improvement on accuracy.Furthermore,for the path planning with multi-target problem,these planning methods need to plan from the needle entry point to the target point for each target, which yields a longer puncture distance and would cause greater damage to human tissues.

A new method of flexible needle trajectory planning based on the bee-foraging learning particle swarm optimization(BFL-PSO) algorithm and the needle retraction strategy is proposed in this paper.First of all,the movement of the needle after penetrating the human body is analyzed, and the objective function which includes puncture path error,puncture path length,and collision function is established.Then,the BFL-PSO algorithm and the needle retraction strategy are analyzed. Finally, medical images of the tissue to be punctured are obtained by MR,and the 3D model of the punctured environment is constructed by 3D Slicer to obtain the environment information on targets and obstacles, and the path of flexible needle is carried out based on the BFL-PSO optimization algorithm and the needle retraction strategy. The contributions of this work are summarized as follows:

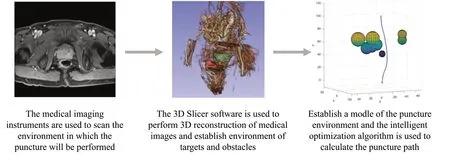
Fig.1 The overall process of puncture path planning with bevel-tip flexible needle

1. To improve the accuracy of path planning for the flexible needle with bevel tip,a new path planning method is proposed.The planning accuracy of this method is higher,and the error is less than 0.001mm in the 3D environmentwithmultipleobstacles.Comparedwiththegeneral method,the planning accuracy of the proposed method is improved by 2–3 orders of magnitude.

2. In the 3D environment,aiming at solving the path planning with multi-targets,the needle retraction strategy is used to reduce the length of the puncture path and reduce the harm to the patient under the premise of ensuring the accuracy of puncture and effectively avoiding obstacles,and it has good adaptability to the multi-target path planning problem.

The rest of this paper is organized as follows. In Sect.2, the 3D reconstruction of puncture environment, needle movement, and objective function are analyzed. The BFLPSO algorithm and the insertion strategy of the needle are introduced in Sects.3 and 4,respectively.In Sect.5,the 3D reconstruction of MR images is carried out and the performance of the multi-target path planning method based on the proposed method in this paper is verified by simulation experiments.Finally,the conclusion is provided in Sect.6.

2 Puncture environment and kinematics of bevel-tip flexible needle

In percutaneous interventional diagnostic surgery, it is desired to avoid introducing harm to important organs such as bones and arteries.Therefore,it is a necessity to obtain information about those important organs and obstacles before puncturing.As shown in Fig.1,to determine environmental information, first, medical images of the tissue to be punctured are obtained by medical imaging instruments such as MR,and then,3D reconstruction of medical images was carried out by the computer to construct the simulation model of the puncture environment and determine the location of obstacles and targets in the puncture environment. After determining the specific environment of the puncture operation, the movement analysis of the flexible needle can be carried out next,which is the main goal of this study.

In this work,it is defined that the flexible needle is rigidly connected in the axial direction, the punctured tissue is isotropic, uniform, and not deformed. As shown in Fig.2,after the needle tip is inserted into the human tissue,the needle tip will be subjected to downward pressure perpendicular to the oblique surface of the needle due to the squeezing of the tissue.The asymmetric force on the incline of the needle tip will change the needle trajectory. Webster et al. proved through experiments that under ideal conditions,the radiusrof the needle trajectory is constant,and the insertion velocity has little effect on the curvature of the flexible needle[25].

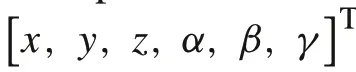
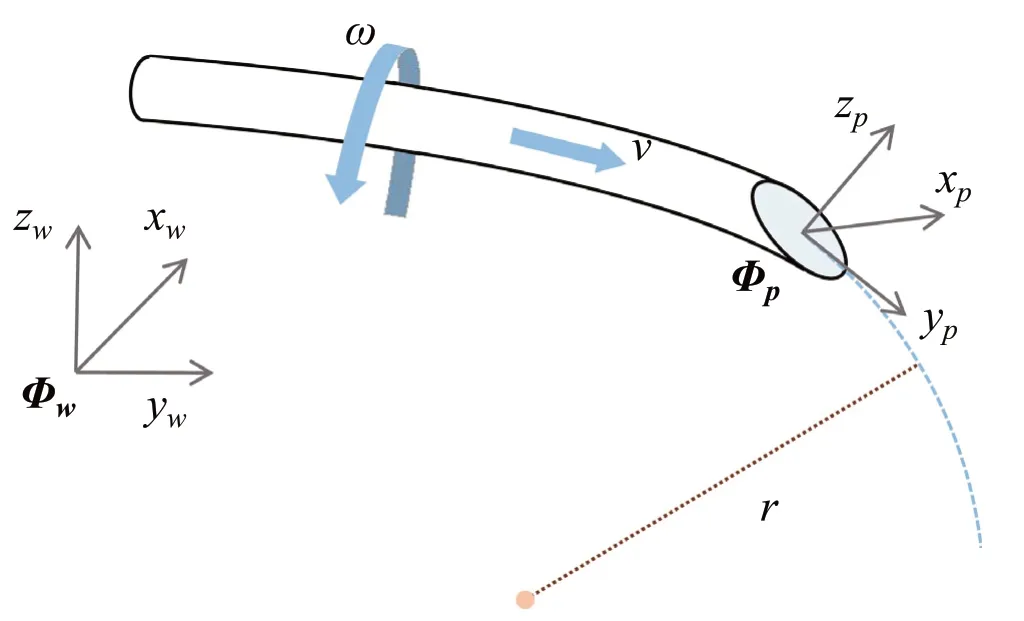
Fig.3 The movement of the flexible needle in 3D space

Theradiusofflexibleneedletrajectorywithbevel-tipremains constant in 3D space,and the velocity of the needle tip in the local coordinate systemΦpis

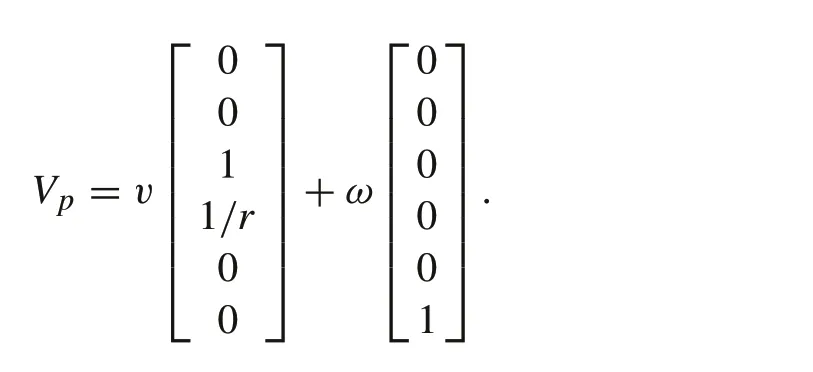
The relationship between the needle tip local coordinate system and the world coordinate system is

wherePis the rotation matrix between the needle tip local coordinate system and the world coordinate system.PΩis the matrix coefficient of the Euler kinematics equation of the vertex motion of a rigid body

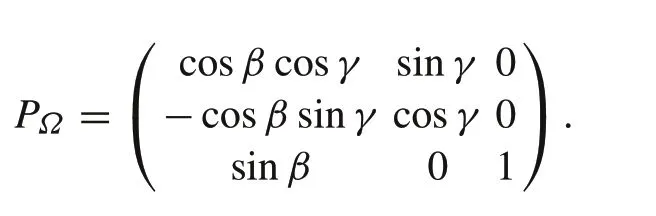
According to Eqs.(1)and(2),the kinematics model is

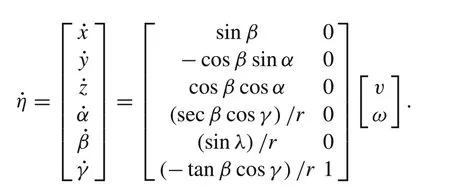
Duindam et al.demonstrated that the puncture trajectory of a flexible needle is independent of the puncture speed and the rotation angle;see the details in[26].Therefore,the

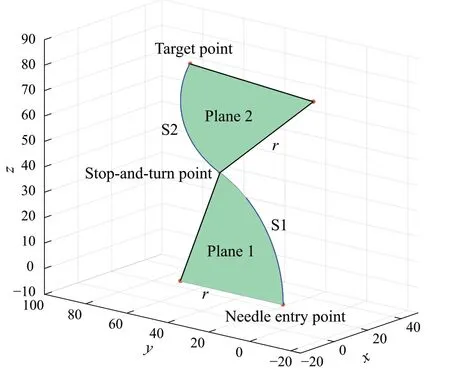
Fig.4 Schematic diagram of segmented path

variable of time can be separated from the control variable,so the system model is transformed into

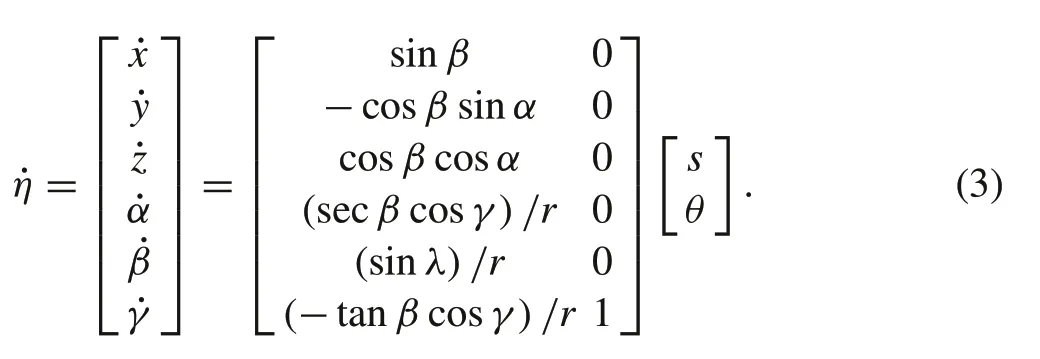
According to Eq.(3),the needle tip advance distancesand the rotation angleθcan be used as the control variable of the needle tip movement[27].Using stop-and-turn strategy[28],the puncture trajectory is completely determined by the sequenceΘ= [(s1,θ1),(s2,θ2),...,(sn,θn)], wherenis the path segment number. The whole needle’s trajectory is composed ofnsegments,and the trajectory of needle tip is shown in Fig.4.

It is assumed that the coordinate of the target isPtarget,the puncture end point determined by the control sequenceΘisPtip(Θ),the puncture path error is the distance betweenPtargetandPtip(Θ),so the puncture path error is calculated as

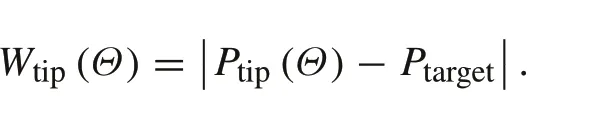
The total length of the puncture path is

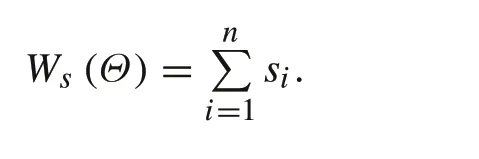
During the puncture process, if the needle tip does not deflect,it will move in the trajectory with a fixed curvature.If the rotation angle of the needle tip isπ,the plane of motion of the tip will not change.If the rotation angle of the needle tip is notπ, it will move into another plane of motion. As shown in Fig.4, since the puncture path control sequence is composed of the combination ofsandθ, and during the puncture process, the stop-and-turn strategy is adopted. In the example shown in Fig.4,the initial position of the needle tip is the needle entry point. First, the needle tip is rotated at the needle entry point to adjust the bevel orientation of the needle tip, and then, the needle tip moves forward S1 to the stop-and-turn point.The needle tip is rotated again at the stop-and-turn point to adjust the bevel orientation of the needle tip. Finally, the needle tip moves forward S2 to the target point.

Remark 1The stop-and-turn strategy is divided into needle insertion action and needle tip rotating action.First,the needle tip rotating action is performed at the current stopand-turn point,and then,the needle insertion action will be performed. At this time, the needle tip reaches the second stop-and-turnpoint.Next,repeattheneedletiprotatingaction and insertion action to complete the puncture path planning.Finally,the entire puncture path is composed of several arc segments.

To plan the puncture path,the objective function is chosen to reflect the length of the path, the deviation between the target point and the end point of the path,and indication of the needle collision with obstacles.It is given by

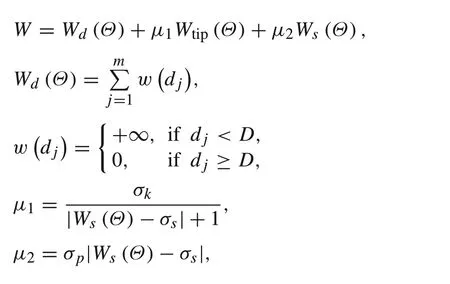
whereμ1andμ2are weights for path error and path length,respectively.σk,σsandσpare the coefficients adjusted according to the simulation results.Wd(Θ)is the judgment function of the obstacle collides with needle,w(d) is the collision function,mis the number of obstacles,d jis the distance between the needle path and thejth obstacle,Dis the safety distance between the obstacle and the needle path,and the value ofwd jwill be set to+∞if the needle path collides with obstacles;otherwise,the value is zero.

3 Bee-foraging learning particle swarm optimization algorithm

The classic optimization methods include gradient descent method,Newton method and quasi-Newton method,conjugategradientmethod,andheuristicmethodhavebeenapplied to solve various engineering problems.Compared with other optimization methods,the heuristic one is simplest to implement in computing resources; among which, the common heuristic optimization algorithms are simulated annealing algorithm, genetic algorithm, and PSO algorithm. In this paper, PSO algorithm is used to solve the puncture path because it has a simple structure,fast computation speed,and wide application[29–31].In recent years,various PSO algorithms have been proposed,but most of them do not enhance the search strategy for the particles with good performance in the search process.In addition,the fitness value of some particles does not continue to improve after a certain number of iterations. These particles may stagnate and there is no strategy to deal with this problem,which leads to poor optimization results.Inspired by Chen et al.[32],in this work,an improved PSO algorithm based on the bee-foraging learning strategy will be adapted to solve the puncture path planning problem.

Similar to other heuristic swarm intelligence algorithms,the artificial bee colony is a swarm intelligence algorithm strategy inspired by bee colony foraging behavior, but bee colony strategy has the characteristics of the division of labor, which divides bee colony into three groups, namely employed bees, onlookers, and scouts [33–35]. Employed bees are responsible for searching for better food source near a certain food source,onlooker bees conduct enhanced searcharoundfoodsourceswhichhasbetterfitnessvalue,and scout bees conducts the random search when a certain food source is exhausted.By combining the artificial bee colony with the PSO algorithm,a new PSO algorithm with the beeforaging learning model (BFL-PSO) is proposed. The BFL model divides the original PSO algorithm into three stages:employed learning, onlooker learning, and scout learning.The employed learning stage is equivalent to the optimization stage of the traditional PSO algorithm,the onlooker learning stage further enhances the search around the particles with better fitness values,and the scout learning stage initializes the particles whose fitness values have not improved after a certain number of iterations.

The employment learning stage is the same as the optimization process of the traditional PSO algorithm, and its update equations are

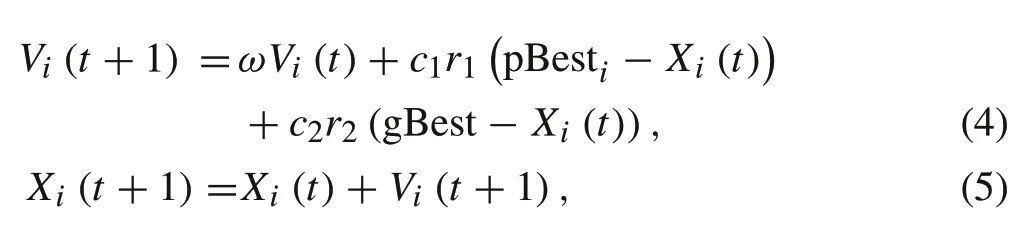
whereViis the velocity of theith particle,Xiis the position of theith particle,tis the number of the current iteration,c1andc2are learning factors,r1andr2are uniformly distributed random numbers in the interval[0,1],pBestiis the historical optimal position of theith particle, gBest is the historical optimal position for all particles,andωis the inertia weight.The update equation ofωis

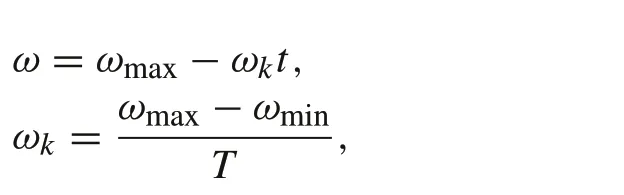
whereωmaxandωminare the maximum and minimum values of inertia weight,respectively,andTis the total number of iterations.

The update situation of each particle will be recorded,while the algorithm is searching for optimization,as shown in Eq.(6).If the current optimal fitness value of a particle is not further optimized after a certain iteration,its counter will be increased. Instead, the current optimal fitness value of a particle is further optimized after a certain iteration,and its counter will be reset to zero

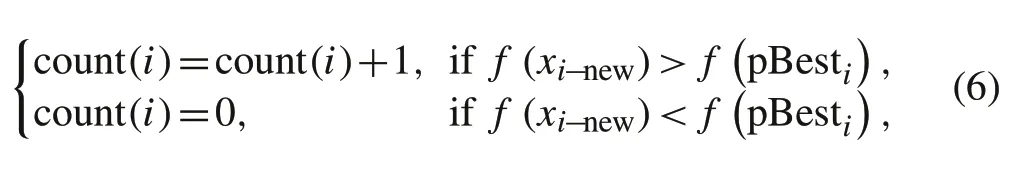
where count(i)andxi−neware the counter and new position for theith particle,respectively,f(xi−new)is the fitness for the new position of theith particle, andfpBestiis the optimal fitness of theith particle.

In the onlooker learning stage, the fitness value is first calculated according to the optimal position of each particle,and the calculation formula is shown as Eq.(7).According to Eq.(8),the probability of each particle is obtained

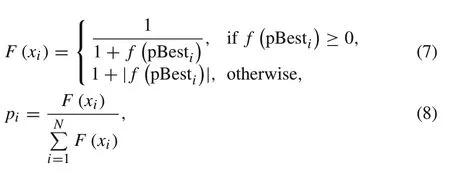
whereNis the number of the particles.

According to the probability obtained by Eq. (8), the roulette strategy is used to select the particles. If a particle is selected, its velocity and position will be updated using Eqs. (4) and (5). If the updated position is better than the original one,the counter of the particle will be reset to zero;otherwise,it will be increased.

In the scout learning stage, if the adaptive value of theith particle has not been improved after iteration,that is,the particle’s counter has reached the upper limit of counting,then the positionxiand velocityviof the particle will be reinitialized.

4 Needle retraction strategy

In the existing literature,a new path planning process should be re-performed when there are multiple targets.Due to the fact that the overall distance of the puncture path planning results using this strategy would be become longer, and it will undoubtedly increase the operation time,causing more unnecessary damage to healthy tissues, and increasing the pain of patients.It has been shown in some experiments that when the needle retracts, the trajectory of the needle is the same as that of the needle before retracts [36]. Inspired by Aghdam et al. [37], a path planning strategy with needle retraction will be adopted in this work.

In the 3D environment,when dealing with the problem of multiple targets,first,all targets are sorted from large to small according to theZ-axis coordinates of the target points,and this order is the order of path planning for each target.Then,the path will be planed for the first target point. As shown in Fig.5,after the initial path planning is completed,a new planning operation will start for the second target from the end of the initial path.If the path to the second target cannot be planned at the end point, the needle tip will retreat to the final position of stop-and-turn, and then carry out path planning for the second target again,and so on,until the path to the second target is planned successfully. If the path of the second target point is not successfully planned until the needle tip retreat to the needle entry point,the path planning will be restarted.Finally,according to this strategy,the path is carried out for all the target points.

The structure diagram of the method proposed in this work is shown in Fig.6.

5 Experiment

To verify the effectiveness of the proposed method in this paper, the general PSO [38], the adaptive intelligent PSO(AI-PSO)[39],and the reinforcement learning method[23]are used as comparison algorithms.

First, 3D reconstruction is performed based on MR images. Import the MR images into 3D Slicer. The Volume Rendering module is used for 3D reconstruction of MR images.As shown in Figs.7 and 8,the Segment Editor module is used to mark obstacles and the prostate area to be punctured,and the Annotations module is used to mark the coordinates of specific obstacles and puncture points.

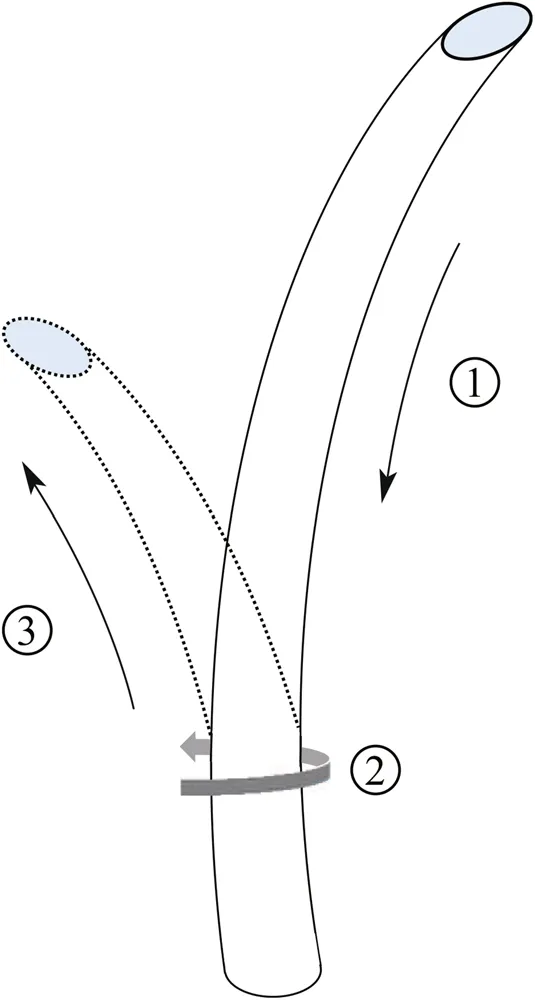
Fig.5 Schematic diagram of needle tip retreat:①The needle tip retreats along the original track.②The needle tip rotates at a certain angle.③The tip of the needle moves in the other direction

Second,for the convenience of processing and calculation in the simulation,the obstacles are assumed to be spherical in this work.Because all the points marked after the 3D reconstruction are negative inzcoordinates,thezcoordinate of the entry point is shifted to 0,and thezcoordinates of other points are moved up to the positive half axis of theZaxis based on thezcoordinate of the needle entry point.Finally,the coordinate of the entry point is [−13,−20,0], the coordinates of the target points are [−19,−15,105], [−14,−29,101],[−16,−28,97], [−16, −21,94], the coordinates of the obstacles are[−14,−3,70],[−14,22,70],[−14,−10,60],[−11,6, 55], [−11,−3,57], [−16,−53,65], [−16,−53,74],[−13,−20,45],and the radii of the obstacles are 11mm,11mm,9mm,9mm,9mm,7mm,7mm,and 5mm,respectively.

Fig.7 3D reconstruction of MR images of prostate region

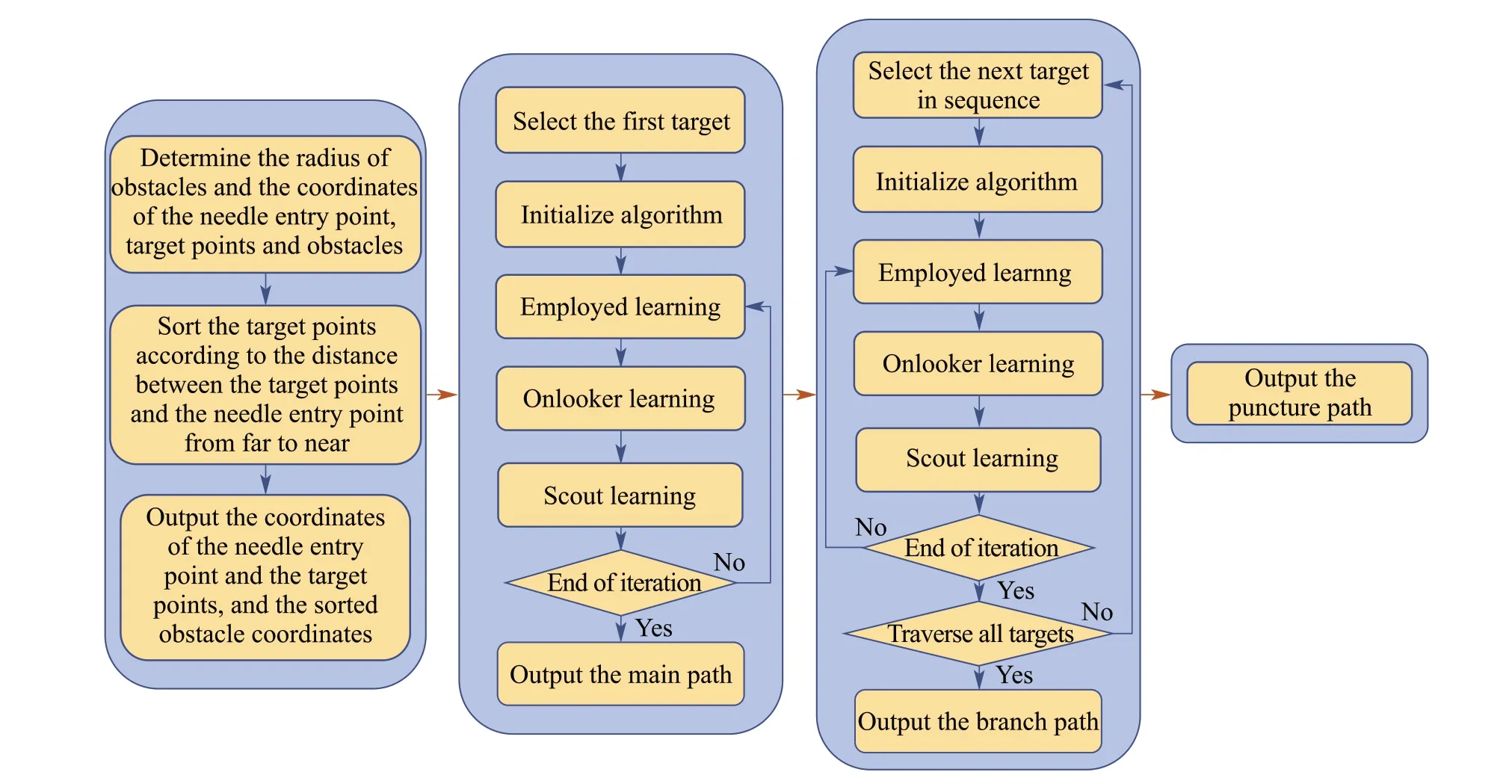
Fig.6 The structure diagram of the algorithm proposed in this paper

Simulation studies are carried out in 3D space.The needle trajectory radius is assumed to ber= 50mm.The parameters in the BFL-PSO algorithm are as follows:the maximum number of iterations isT=2000,the particles numberNis 40,c1=1,c2=2,ωmax=1.5,andωmin=0.5.

First, 50 single target path planning simulation experiments are carried out based on the BFL-PSO algorithm in 3D space,and the results are compared with those obtained by general PSO algorithm,AI-PSO algorithm,and reinforcement learning method.The objective function of the method based on the general PSO algorithm includes two optimization objectives: path deviation and the path do not collide with obstacles. The optimization objective function of the method based on the AI-PSO algorithm is the same as the objective function of this work, but the parameters of the algorithm can be adjusted adaptively.The method based on reinforcement learning uses the universal distributional Qlearning(UDQL)framework to learn the steering policy of flexible needles to plan the path.The path simulation diagram result based on the BFL-PSO algorithm is shown in Fig.9,and the comparison results are shown in Table 1.

Second, only the targets and needle retraction strategy are added, while the obstacles remain the same, 50 times of multi-target puncture path planning are carried out under the BFL-PSO algorithm with needle retraction strategy in 3D space,and the results of path planning were compared with those without the strategy of needle retreating.The simulation results are shown in Figs.10 and 11,Tables 2 and 3.

By analyzing the data in Table 1, collected under 50 single target path planning experiments, the average path error calculated by BFL-PSO algorithm is 7.05E–04mm,the maximum error is 9.76E–04mm,and the minimum error is 9.51E–05mm.As shown in Fig.9,the puncture path planned by BFL-PSO algorithm completely avoids the obstacles in the puncture environment and accurately reaches the target.

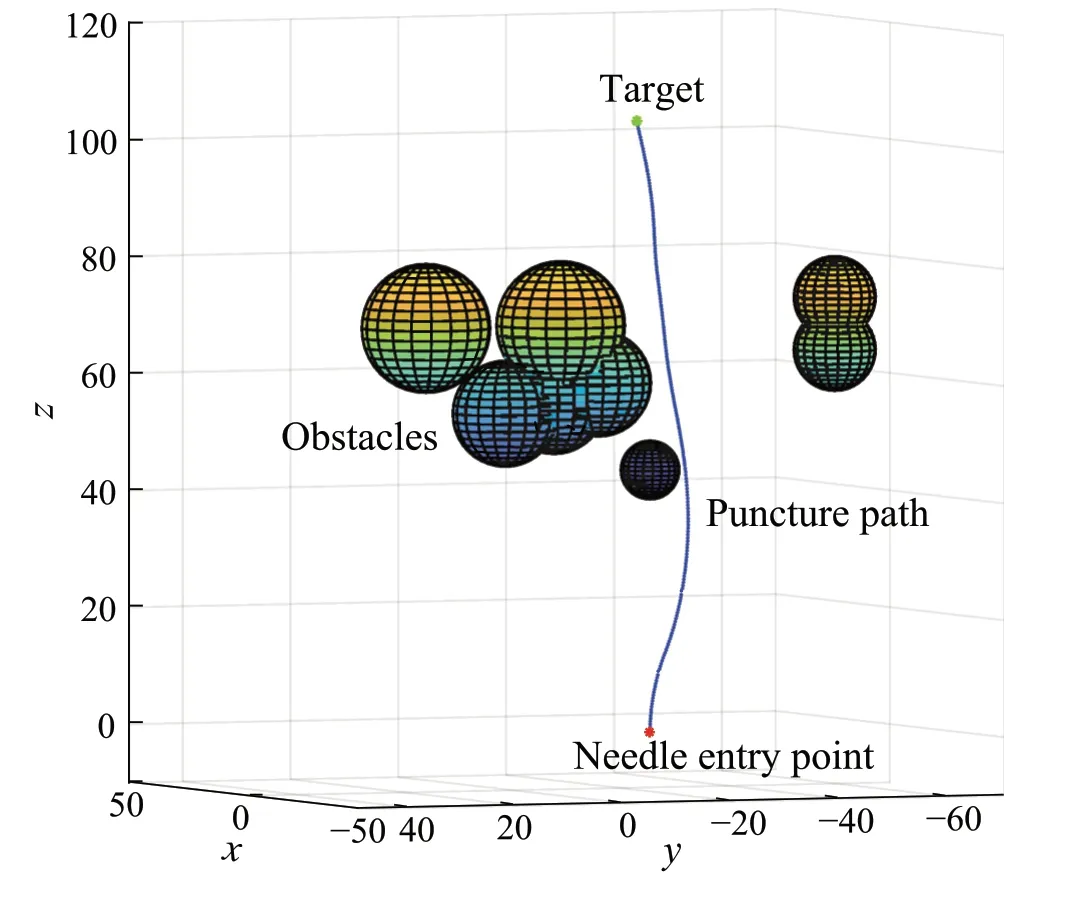
Fig.9 An schematic diagram of single target puncture planning based on BFL-PSO algorithm

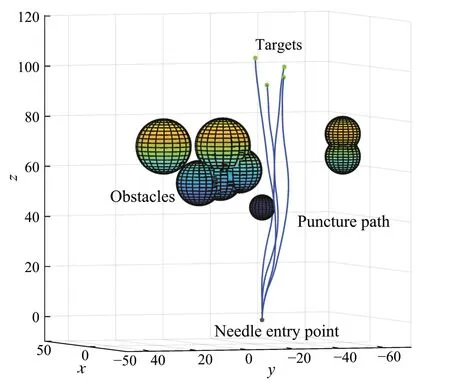
Fig.10 The path obtained by the BFL-PSO algorithm without needle retraction strategy

In the case of multiple targets, on the basis of the puncture path planning using BFL-PSO algorithm, the needle retraction strategy was added.For each target,it is no longer planned again from the insertion point. Figures10 and 11 show the multi-target puncture path planned without the needle retraction strategy and with the needle retraction strategy,respectively.Both strategies accurately reach each target,but the overall puncture path lengths are quite different. Table 2 shows the overall puncture path length under the two needle insertion strategies. By performing 50 experiments,when using the needle retraction strategy,the maximum total puncture path length was 353.76mm,the minimum one was 302.63mm,and the average one was 329.28mm.Compared with the general bevel-tip flexible needle path planning strat-egy,the needle retraction strategy reduced the total puncture length by 15.5%. For multi-target problems, the planning accuracy of the method based on the BFL-PSO algorithm and the needle retraction strategy still maintains a good level.There is no reduction in planning accuracy due to the increase of targets and the complexity of the planning situation,which indicates that the method proposed in this paper has better adaptability to the multi-target problem.

Table 1 Comparison of puncture path planning errors between different path planning methods for single target problem

Table 2 Comparison of puncture path length between different needle insertion strategies

Table 3 Planning error based on BFL-PSO algorithm with needle retraction strategy for multi-target problem

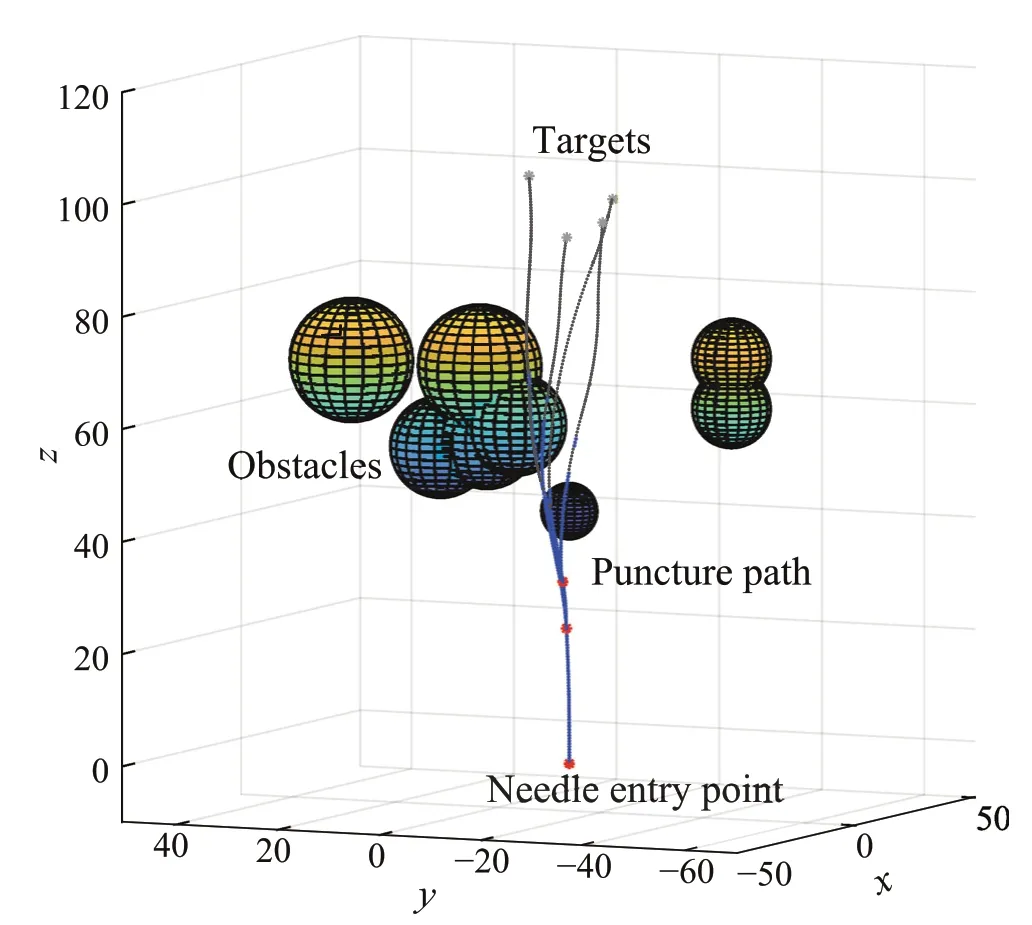
Fig. 11 The path obtained by the BFL-PSO algorithm with needle retraction strategy

6 Conclusion

In this paper,aiming at the multi-target path planning problem of the bevel-tip flexible needle,a new method based on BFL-PSO algorithm with needle retraction strategy in 3D space has been proposed,and the performance comparisons with existing flexible needle path planning methods were addressed.The results showed that the accuracy of the puncture path planned by this path planning method is higher,and the path planning deviation is shown to be less than 0.001mm.The length of the puncture path has been greatly shortened.Compared with the path planning method without needle retraction strategy,the length of the puncture path has been shortened by about 15.5%, and it has good adaptability to the multi-target path planning problem. In this work,although the puncture path error is small, the influence of human respiration and movement on path planning is not considered. In future work, we will consider more external factors to strengthen the capabilities of the algorithm.