基于广义Kelvin 链钢管混凝土徐变研究

2022-02-11陈梦成张明阳温清清

工程力学 2022年2期

杨超，陈梦成，张明阳,3，李骐，方苇，温清清

(1.华东交通大学土木建筑学院，南昌 330013；2.轨道交通基础设施性能监测与保障国家重点实验室，南昌 330013；3.江西交通职业技术学院建筑工程系，南昌 330013)

钢管混凝土结构因优越力学性能已被广泛使用在高层和超高层建筑、桥梁、地铁车站等土木工程基础设施中，相关最新研究层出不穷[1-5]。核心混凝土徐变对钢管混凝土结构性能具有重要影响，钢管与混凝土组合效应使得分析该结构时变性能问题更为困难。因此，钢管混凝土徐变研究具有重要理论和实践意义[6-7]。

钢管内核心混凝土受力状态复杂，为三向应力状态。国内外至今仍然没有对钢管混凝土徐变计算提出一个统一的计算方法。因此，钢管混凝土徐变研究依然是目前研究热点。韩林海等[8-9]采用试验和有限元计算相结合的方法，讨论了氯离子侵蚀和长期荷载耦合作用下钢管混凝土力学性能问题，陈宝春等[10]建立了钢管混凝土拱桥徐变预测模型，王玉银等[11]采用试验技术和有限元分析方法讨论了钢管混凝土非线性徐变问题，郝兆峰等[12]采用试验方法探讨了带缺陷钢管混凝土的徐变问题，刘伟等[13]对钢管再生混凝土徐变问题进行了试验研究，肖思柯等[14]研究了考虑非线性徐变的钢管混凝土柱稳定承载力计算问题，丁敏等[15]建立了钢管混凝土轴心构件徐变预测模型，并用该模型进行了徐变性能分析。

上述研究在讨论钢管混凝土徐变问题时，大多都是以单向应力状态混凝土徐变模型为基础。事实上，正如前文所述，钢管核心混凝土受力状态为三向应力状态，徐变性能复杂。试验表明[16-17]，在三向应力状态下，应该考虑徐变Poisson 效应。三向应力作用下徐变不能用单向应力作用下徐变规律推算，应该考虑三向应力的相互作用。近年来，有不少文献论证这一观点[18]。王元丰等[19]在在分析钢管混凝土徐变试验数据后，认为若要准确计算钢管混凝土徐变，需要对现有基于单轴应力徐变试验得到徐变模型进行修正，并建立了相应的计算模型；Li 等[20]和张电杰等[21]引入徐变泊松比效应[22]，讨论了钢管混凝土徐变的计算方法。然而，目前三向应力状态下混凝土徐变的研究仍不成熟[23-24]。

本文根据粘弹性理论和徐变叠加原理，采用多参数Kelvin 元件链粘弹性模型，建立三维应力状态下的钢管混凝土徐变计算方法，并嵌入有限元软件Ansys 中，用Fortran 语言编程，建立相应有限元数值分析模型。模型参数近似表示为连续粘滞谱。为验证该方法的可行性和有效性，本文还将进行钢管混凝土徐变试验。

1 单向应力状态下混凝土徐变本构模型

根据粘弹性理论[25]，单向应力作用下混凝土徐变可表示成第一类Volterra 积分方程：

式中：t为混凝土龄期；t′为荷载龄期；σ为应力；ε为应变；ε0(t)为非弹性应变(除作用力以外如温度引起的热膨胀和收缩等产生的应变)，本文假定ε0(t)=0；J(t,t′)为徐变函数(也称为徐变柔度函数)，定义为单位应力作用下t-t′时间内引起的总应变。它可表示为Dirichlet 级数形式[25]：

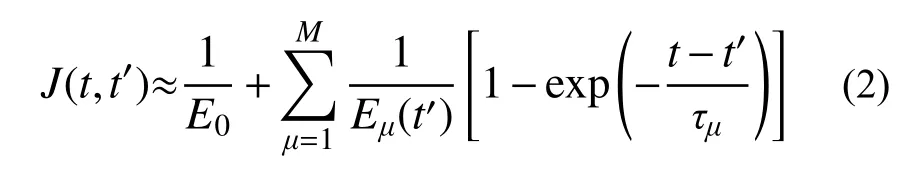
式中，第1 项可以理解为一个牛顿弹性元件在单位力作用下引起的弹性应变，第2 项可以理解为M个Kelvin 元件在单位力作用下引起的总应变，如图1 所示。Kelvin 元件个数M的选取取决于混凝土徐变计算精度，一般来说，M取得越大，精度越高；E0为弹性模量；τμ为粘滞时间；Eμ(t′)为荷载龄期相关瞬时弹性模量，由连续粘滞谱A(τμ)表示[25]：

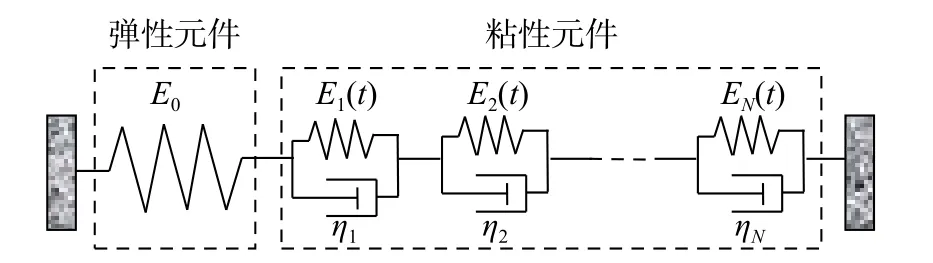
图1 广义Kelvin 混凝土徐变模型Fig.1 Generalized Kelvin chain for concrete creep model

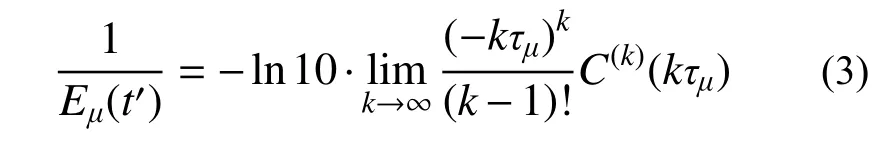
式中：C(k)(kτμ)为徐变度C(t,t′)对t的k阶导数；C(t,t′)=J(t,t′)-1/E0；经验表明：当k=3 的时候，计算可满足精度要求。

将式(3)代入式(1)中第一式，可得：

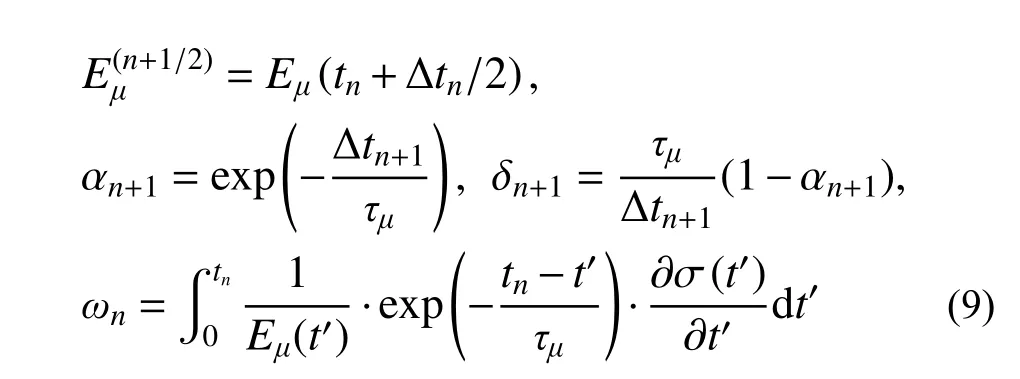
式(8)与文献[26]用率型法得到的结果完全一致。

通过分步积分法，式(9)中最后一式ωn可以进一步改写为：

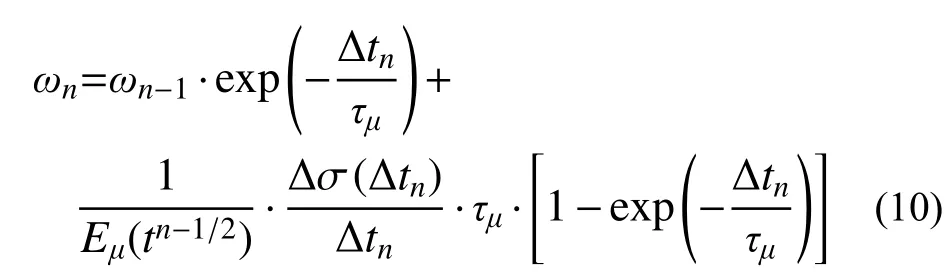
式中，ω0=0。

将式(8)代入式(4)，得到单向应力状态下考虑混凝土徐变的总应变增量为：

式(12)即为单向应力状态下混凝土徐变应力应变增量本构关系。

2 钢管混凝土徐变本构模型

对钢管混凝土结构而言，核心混凝土的徐变应力状态具有明显的三向特性。目前，国内外对三向应力状态下的混凝土徐变的研究尚未成熟，没有可直接借鉴的三向应力状态下徐变计算模型。因此，本文参考Neville 等[16]、王元丰和韩冰等[18]以及李世伟和杨永清等[24]做法，拟采用泊松比效应，把单向应力状态下混凝土徐变计算模型推广到三向应力状态。假定三向应力状态下，三个方向徐变泊松比分别为μc1、μc2和μc3，则根据应力-应变弹性本构关系，可得到如下转换矩阵：

对于钢管混凝土结构而言，轴向荷载作用下，根据弹性力学理论，式(15)可进一步改写为：

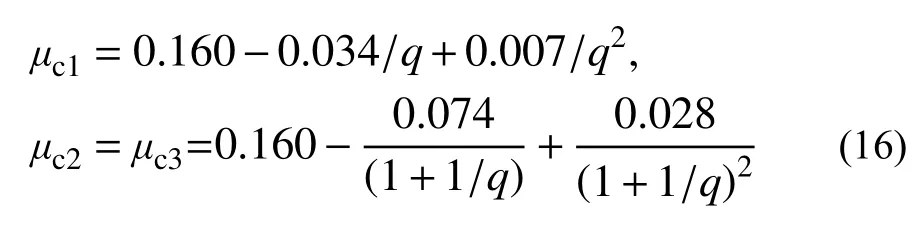
式中：μc1为轴向徐变泊松比；μc2为径向徐变泊松比；μc3为环向徐变泊松比；q为钢管对核心混凝土的紧箍力系数。根据钟善桐[6]的工作，q的表达式为：

式中：μc为混凝土的泊松比；μs为钢材的泊松比；α=As/Ac，As为外钢管的截面积，Ac为核心混凝土的面积；n=Es/Ec，Es为外钢管的弹性模量，Ec为核心混凝土的面积；μc由以下式给出：

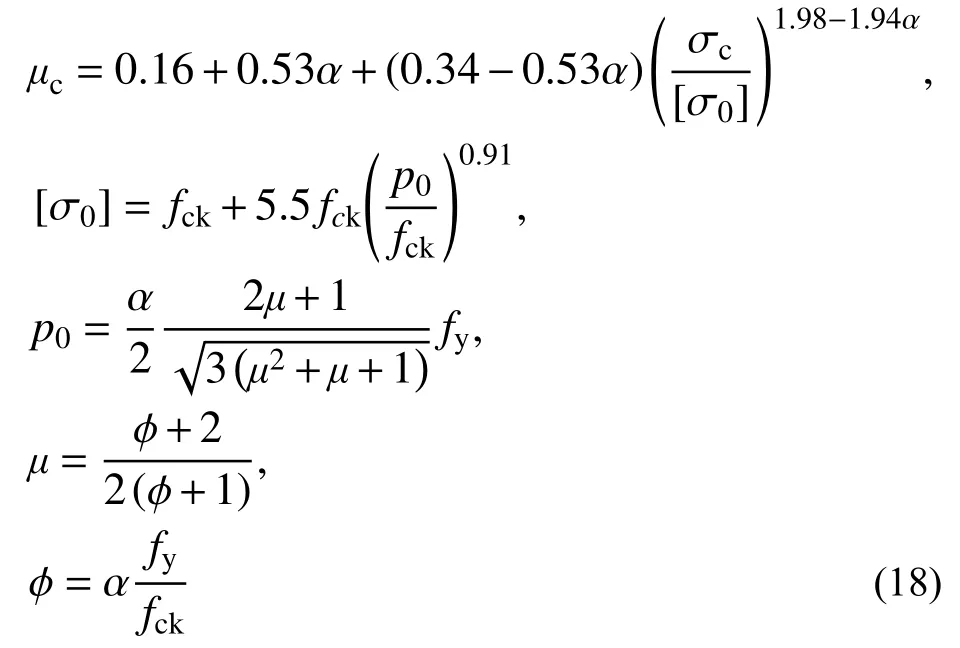
三向应力状态下，有 σx，σy，σz，τxy，τyz，τzx这6 个应力分量和 εx，εy，εz，γxy，γyz，γzx这6 个应变分量。写成矩阵形式：

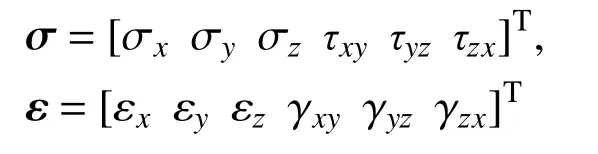
通过引入式(14)中的泊松比效应矩阵，根据粘弹性定律，三向应力状态下的混凝土徐变应力-应变本构关系可由式(1)改写为：

类似于第1 节单向应力状态下混凝土徐变应力-应变本构关系的推导过程，同样，可以从式(19)得到如下形式的三向应力状态下的混凝土徐变应力-应变增量本构关系：

3 钢管混凝土徐变有限元分析

将式(25)获得的位移增量Δun+1代入式(20)，即可求得应力增量Δσn+1。

为实现上述这个数值计算目标，本文采用Fortran 语言二次开发Ansys 子程序Usermat。开发的子程序Usermat 功能可计算每一时步的三向应力状态下混凝土徐变应变增量。在计算混凝土徐变应变增量的过程中，由于相邻时刻的徐变应变增量间存在递推关系(式(22))，因此，当前时刻Δtn+1混凝土徐变应变增量的计算需要调用上一时刻Δtn计算得到的ωn(参见式(21))。

4 算例验证

为了验证本文三向应力状态下钢管混凝土徐变计算模型的有效性和可靠性，本节基于ACI 徐变模型[27]，采用64 位Ansys 15.0+Vsiual Studio 2010+Inter Fortran Composer XE 2013 SP1 对Ansys 用户材料子程序Usermat 进行二次开发，并嵌入到Ansys主程序中，实现长期荷载作用下素混凝土柱和钢管混凝土柱的徐变计算。

4.1 算例1.既有钢管混凝土结构徐变试验

1) 2017 年Chen 等[10]进行了两组共13 个钢管混凝土柱徐变试验。本文选取其中一根试件(CFT-0.3-CR)进行徐变计算验证。该试件钢管直径D为140 mm，壁厚ts为2 mm，长度L为1050 mm。钢管混凝土试件混凝土强度等级为C50，测得圆柱体混凝土强度fcm=62.3 MPa；试件的长期荷载作用轴向压力比为0.30，即端面长期作用荷载为300 kN，加载时混凝土龄期为7 d。有限元计算模型及计算结果对比情况如图2 所示，结果显示本文计算方法得到的结果与原文试验数据吻合良好。

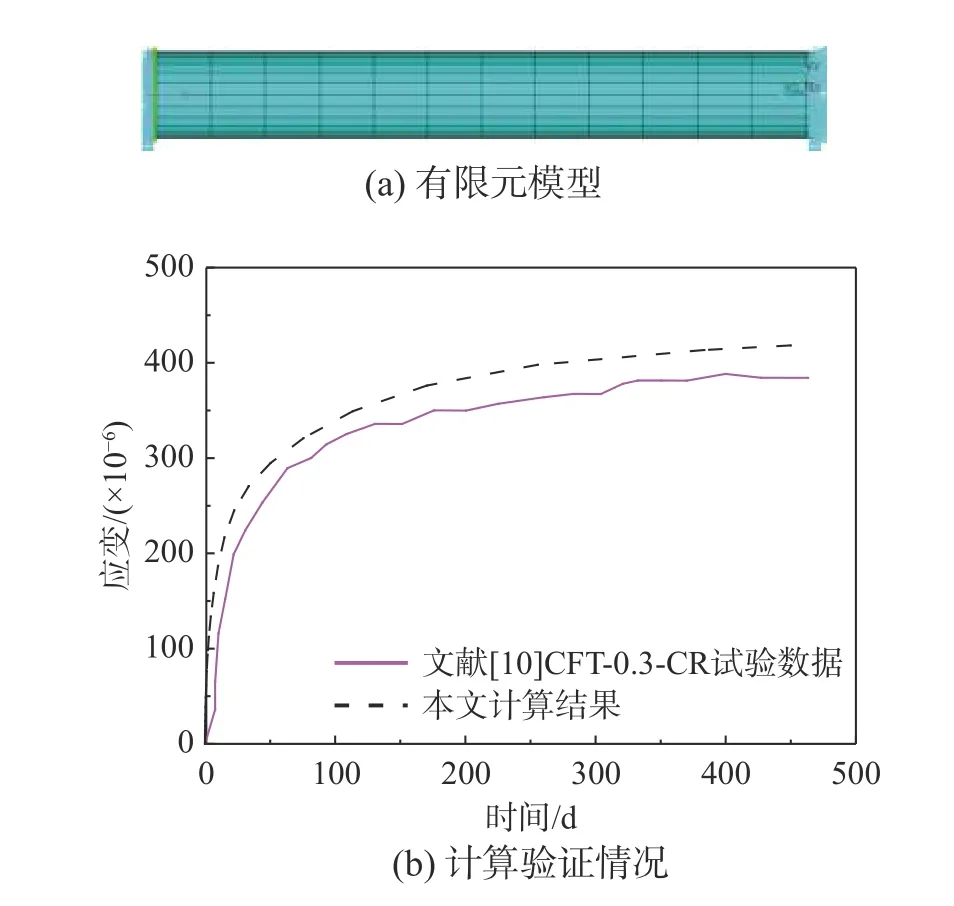
图2 文献[10]钢管混凝土短柱有限元模型及计算验证Fig.2 Finite element model and calculation validations of concrete filled steel tube in [10]

2) 谭素杰、齐加连等[28]在1983 年-1984 年间进行了钢管混凝土柱长期和短期徐变试验。本文选取短期徐变试验中试件号14 进行徐变计算验证。该试件钢管直径D为108 mm，钢管壁厚ts为1.97 mm，长度L为432 mm。钢管混凝土试件核心混凝土立方体强度为33 MPa；钢材屈服点fy=315 MPa，泊松比为0.28，弹性模量Es为220 GPa。试件的长期荷载作用轴向压力比为0.51，即端面长期作用荷载为548 kN。计算结果与试验结果对比情况如图3 所示，本文计算结果与文献[28]试验数据在加载18 d 前吻合良好，之后相对试验数据偏大，基本能够准确描述该徐变试验发展规律。

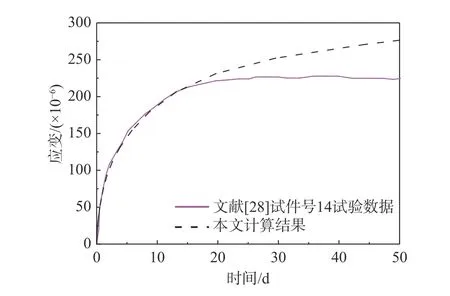
图3 文献[28]钢管混凝土短柱计算验证Fig.3 Calculation validations of concrete filled steel tube in [28]

4.2 算例2.钢管混凝土徐变试验

4.2.1 试件设计与加工

为验证本文提出的钢管混凝土轴压短柱的徐变计算方法，进行试验验证。为避免试件过短使得端部效应影响显著和试件过长而发生压弯破坏，确定试件长径比L/D=3。含钢率设计为0.146。

试验中设计2 个圆形素混凝土短柱，2 个圆形钢管混凝土短柱，长度均为342 mm，混凝土强度等级均为C30，长期荷载作用轴向压力比值为均0.3(实际加载值如表1 所示)，进行为期135 d 的长期试验。钢管名义截面尺寸为：114×3.75 mm2。在灌注混凝土之前，测得各钢管实际厚度见表1。

表1 徐变试验试件一览表Table 1 List of creep test specimens

混凝土养护成型后，核心混凝土表面进行凿毛处理，拌制环氧砂浆填平，待硬化后磨平以保证端板与混凝土能够充分接触，最后围焊上端板。保证混凝土上表面与钢管上表面齐平，从而保证钢管与核心混凝土在加载和持荷阶段共同受力。

4.2.2 材料力学性能

长期荷载作用下的钢管混凝土试件的钢管分别源于6 m 长的冷弯直缝钢管。按照规范[29]制作3 个标准拉伸试件测得钢材的屈服强度fy平均值为398 MPa，极限强度fu平均值为455 MPa。

浇筑钢管混凝土试件同时，预留3 个边长为150 mm 的混凝土立方体试块，标准环境养护至构件轴压试验时测得混凝土抗压强度fcu为44.04 MPa。

4.2.3 试验加载与测试数据

参考文献[11]试验装置，自行设计改进的自平衡加载装置(图4 所示)。试验加载及后期持荷过程中，采用千斤顶配合反力架进行预加载并通过拧紧螺栓实现最终加载。为保证持荷稳定，长期持荷过程中需对试件进行补载。实际试验过程中，当NL降低2%以上时，进行补载，补载频率保证试件荷载满足规范[30]要求。

图4 试验装置Fig.4 Test device

钢管表面中部环向间隔90°对称布置4 组电阻应变片测得钢管应变；同时钢管表面间隔180°布置2 组标距为200 mm 的不锈钢测量端子，采用手持式应变仪测量钢管应变；二者相互校核测量结果，发现所测得试件变形之差不超过5%，验证本文使用的钢管应变测试方法可靠。

4.2.4 试验结果分析与算法验证

徐变试验室是在一定的温度和湿度环境下进行的，试验时室内温度平均为24.04 ℃，湿度平均为59.22%，温度和湿度变化情况如图5 所示。图6给出了素混凝土圆柱与钢管混凝土轴压短柱徐变试验数据，两组试验均包含2 个平行试件。从图中试验数据可以发现，无论是单轴作用下的素混凝土圆柱还是核心混凝土受多轴应力作用下的钢管混凝土短柱，构件的徐变数据均呈现为先快速增长再缓慢增长最终趋于平稳的发展规律，与已有徐变试验结果对比发现[10]，本文徐变试验曲线能够反映一般钢管混凝土徐变发展规律；单轴荷载作用下，素混凝土徐变在持荷60 d 左右趋于稳定；钢管混凝土徐变在持荷30 d 左右趋于稳定；钢管混凝土徐变发展较素混凝土徐变较早趋于稳定，并且徐变终值较素混凝土徐变小。

图5 长期荷载试验过程中温度与湿度变化Fig.5 Variation of temperature and humidity measured during long-term test

图6 试验结果与计算验证Fig.6 Test results and calculation verification

从对比素混凝土徐变数据与钢管混凝土徐变数据可以发现，相同条件下，钢管混凝土徐变较素混凝土徐变小很多。其原因主要由于钢管混凝土徐变过程发生应力重分布使作用力从徐变柔度更大的核心混凝土向蠕变应变率更小的外包钢管转移，外包钢管对构件徐变具有抑制作用；密闭钢管内核心混凝土无法与外界发生水分交换，故几乎不发生干燥收缩和干燥徐变；另外，三向应力状态对核心混凝土徐变度有影响，主要表现为紧箍力引起的横向徐变泊松效应使核心混凝土徐变比素混凝土徐变要小。

图5 给出本文试验数据与计算结果对比情况，结果发现，素混凝土圆柱与钢管混凝土轴压短柱试验数据与本文采用的率型徐变计算方法得到的计算结果均吻合良好，验证了本文方法的适用性。