Aircraft Optimal Separation Allocation Based on Global Optimization Algorithm

，，2*

1. College of Civil Aviation， Nanjing University of Aeronautics and Astronautics， Nanjing 211106， P. R. China；

2. College of Transportation Science and Engineering， Civil Aviation University of China， Tianjin 300300， P. R. China

Abstract: A dynamic programming-sequential quadratic programming （DP-SQP） combined algorithm is proposed to address the problem that the traditional continuous control method has high computational complexity and is easy to fall into local optimal solution. To solve the globally optimal control law sequence， we use the dynamic programming algorithm to discretize the separation control decision-making process into a series of sub-stages based on the time characteristics of the separation allocation model， and recursion from the end stage to the initial stage. The sequential quadratic programming algorithm is then used to solve the optimal return function and the optimal control law for each sub-stage. Comparative simulations of the combined algorithm and the traditional algorithm are designed to validate the superiority of the combined algorithm. Aircraft-following and cross-conflict simulation examples are created to demonstrate the combined algorithm’s adaptability to various conflict scenarios. The simulation results demonstrate the separation deploy strategy’s effectiveness， efficiency， and adaptability.

Key words：optimal separation allocation； sequential quadratic programming； dynamic programming； globally optimal control； optimal control law

0 Introduction

For the existing air traffic control， when there is a potential conflict between aircraft， only the controller can deploy the conflict， which not only increases the workload of controllers but also reduces the interval maintenance efficiency［1］. Therefore，International Civil Aviation Organization （ICAO） Global Air Navigation Plan 2015—2028 （ICAO 9750， Fourth Edition） specifically states that under acceptable air-ground conditions， the pilot can be temporarily authorized to autonomously take charge of and maintain the separation between the owner and the designated traffic［2］. The pilot can independently select the flight speed and altitude during the autonomous separation operation， which improves the pilot’s participation in the flying process and allows the aircraft to fly along a more efficient flight speed profile， hence increasing airspace capacity［3-4］. However， the sharp increase in the number of aircraft and the improvement of pilot autonomy also raise the possibility of a flight conflict. Therefore， the study of aircraft separation control has important theoretical value for the development of a new generation of air traffic management［5］. In recent years， studies have focused on the aircraft separation control methods， which are classified as the discrete conflict resolution or the continuous conflict resolution based on different optimization models.

The discrete resolution methods， according to the conflict resolution process， discretize the resolution process into equal intervals from the dimension of time or distance， and then use the discrete optimization for optimization calculation to obtain the conflict resolution control law that makes the entire system optimal. The ant colony algorithm is a widely known method for dealing with discrete liberation problems. It searches pheromones of different paths to find the optimal conflict-free trajectory［6］. The traditional ant colony algorithm only uses the direction adjustment strategy. Tang et al.［7］extended the traditional ant colony algorithm with a sorting system to introduce speed and direction adjustment strategies to the conflicting aircrafts. However， the ant colony algorithm is susceptible to local optimization and suffers from a high computational workload with a slow convergence speed. Moreover， the genetic algorithm is capable of performing global searche. It uses cross mutation decision variables to obtain the optimal trajectory under specified constraints［8］， and adopts a trajectory generation function and a detection function to predict future flight conflicts［9］. But its accuracy depends on empirical characteristics， which makes it difficult to predict flight conflicts in the absence of historical data and samples. Furthermore， considering the impact of external environment changes at different stages on flight conflicts， researchers use the probability transformation method to obtain the probability density function of the minimum distance between aircraft from the probability density function of wind component， so as to obtain the conflict probability［10-11］. The discrete resolution method solves the model mismatch caused by changes in aircraft state or external environment in each time period or distance period， which is closer to the real situation. However， it has the defects of large amount of calculation and a slow convergence speed. Additionally， the calculation accuracy of the discrete resolution is affected by initial samples and empirical parameters.

The continuous resolution method is to calculate the optimal conflict free trajectory of the aircraft by using relief strategies such as heading， speed and altitude adjustment with the optimal control theory. Trajectory based operation （TBO） is the core of the next generation air transportation system in the United States. Conflicts can be effectively avoided by transforming the shortest separation problem into the arrival time of designated waypoints［12］. Using the method of geometric analysis and formula derivation， conflict free trajectories［13-14］can be deduced only by specifying the 4D waypoints of an aircraft under the conditions， including aircraft acceleration， speed limits and flight intervals. Based on the current status of aircraft and route constraints［15］， the efficiency of separation maintenance strategy can be effectively improved by specifying aircraft direction［16-17］and speed adjustment rules［18］. However， such algorithms are only suitable for simple constraints， and cannot obtain the optimality of conflict free trajectories. In actual operations， an aircraft flight is a complex nonlinear motion， so its conflict resolution problem is a nonlinear programming problem with complex constraints. To solve this problem， experts proposed an aircraft-following model from the initial point to the end point. Moreover， the introduced algorithms such as Pontryagin minimum principle［19］， interior point penalty function method［20-21］， and sequential quadratic programming［22-23］transform the multi-constraint optimal control problem into nonlinear programming problem［24］to obtain the optimal control law of aircraft following. Despite the fact that this method can solve the control problem’s optimal solution， it is difficult to verify the global optimality of the solution. The continuous resolution algorithm thus has the advantages of reduced computation time and great precision as compared to the discrete resolution technique， but it is simple to settle on the local optimal solution.

To sum up， the calculation accuracy of the discrete resolution method is heavily dependent on the degree of discretization and empirical parameters， whereases the continuous resolution methods are difficult to solve cases with complex constraints and find the local optimal solution. Therefore， this paper adopts the optimal control method of continuous resolution and proposes a combined separation control algorithm based on dynamic programming and sequential quadratic programming to ensure the global optimality of the calculation results. First， the aircraft following model under sequential flight conditions is established， and the flight time from the initial point to the end point is decomposed intonsub-stages in the time dimension. Second， the recursive expression from the end stage to the initial stage is established by employing the dynamic programming algorithm， and the sequential quadratic programming algorithm is used to calculate the optimal return function for each sub-stage. Finally， the combined algorithm is compared with the traditional interior-point penalty function algorithm. And two conflict scenarios， the aircraft-following and the cross-conflict， are designed to verify the effectiveness and adaptability of the combined algorithm.

1 Aircraft Separation Model

In this study， the definition of a protected area is introduced in conflict detection and separation control， that is， the circular area withras the radius， and the aircraft centroid as the center. It is determined that the ownship intrudes into the protected area of the designed aircraft as a conflict， and two typical conflict scenarios with potential conflict are considered. （1） Following conflict： The designed aircraft and the ownship are flying on the same route， and the separation between the two aircraft tends to decrease. （2） Horizontal cross-conflict： The designed aircraft and the ownship cross flying on the intersected air routes， and the separation between the pairs of aircraft tends to decrease.

1.1 Following conflict model

The aircraft-following characteristics of air traffic flow are mainly reflected in the operation of aircraft queuing on congested routes. This work focuses on the phase of cruise， in which the aircraft rarely adjusts the flight altitude. Considering the complexity of the algorithm， this work ignores heading adjustment and restricts to the speed adjustment. It is assumed that the two aircraft are flying with the same direction， route， and vertical altitude， and that the pilot strictly abides by the initial 4D flight trajectory. Assuming that the front aircraft flies at a constant speed along the route， the following aircraft will start to execute the speed adjustment strategy immediately while detecting the conflict risk.

The following model coordinate system of the designed aircraft and the ownship is shown in Fig.1. It is assumed that at the initial moment， the position of the designed aircraft isA=(x1+d1，0)， and its speed isW. The position of the ownship isB=(x1，0)， and its speed isV1. At the end time， the ownship reaches the designated end pointBn=(xn，0)， and the position of the designed aircraft at this point is denoted asAn=(xn+dn，0). The determination of the conflict can be expressed by the relative positional relationship of the two aircraft. In the case where the two aircraft keep their initial speed until the ownship passes through the designated terminal point， the conflict can be determined when the following expression is satisfied

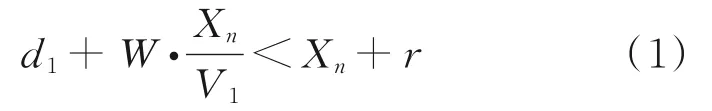
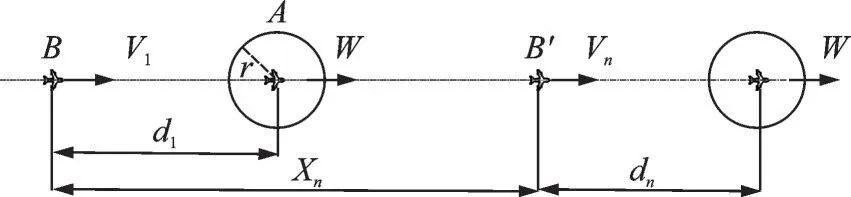
Fig.1 Following model coordinate system

The accelerationais considered to be the control law of the separation allocation algorithm for conflict scenarios. It is assumed thatkrepresents the state of separation control， and the time period between two adjacent stages is Δt， The speed of the ownshipVsatisfies

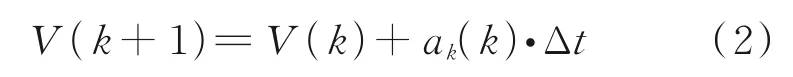
Actual distance between two aircraftdkis defined as

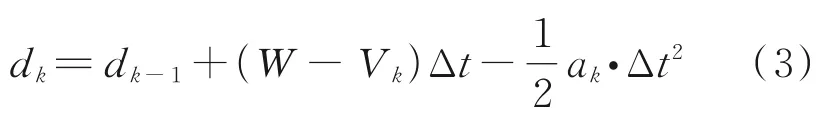
Considering the optimal arrival time and fuel consumption， the final goal of the separation allocation strategy is to reduce the adjustment of aircraft acceleration， while minimizing the time delay of the ownship to reach the end point. Besides， the acceleration range [amin，amax] of the aircraft needs to be restricted to prevent aircraft speed adjustment from exceeding its performance limit and ensure the feasibility of the strategy. To ensure the conflict can be solved， it is necessary to calculate the shortest end distanceXnmin， that is， the displacement of the ownship in the process of decelerating fromV1toWwithamin

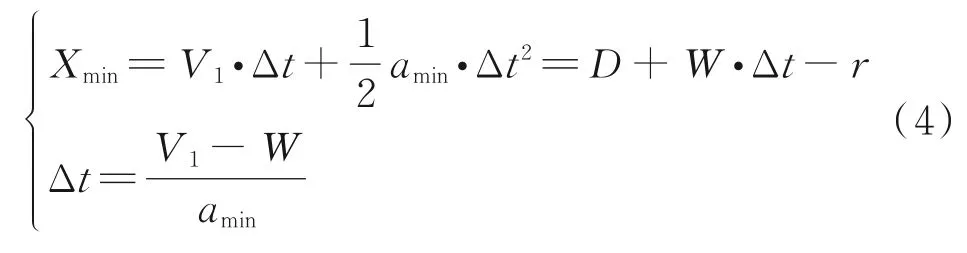
1.2 Cross-conflict model

Fig.2 shows a cross-conflict model of two aircraft. The current route of the two aircraft is intersected atXn. And there is a potential conflict risk， if the two aircraft continue to fly along their routes. Based on the assumptions made in the previous section， it is assumed that the ownshipBand the designed aircraftAboth fly based on the 4D flight path， and then the flight paths of the two aircraft are defined as

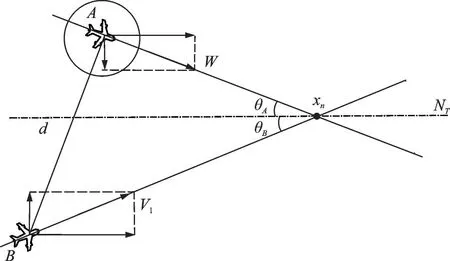
Fig.2 Cross-conflict model

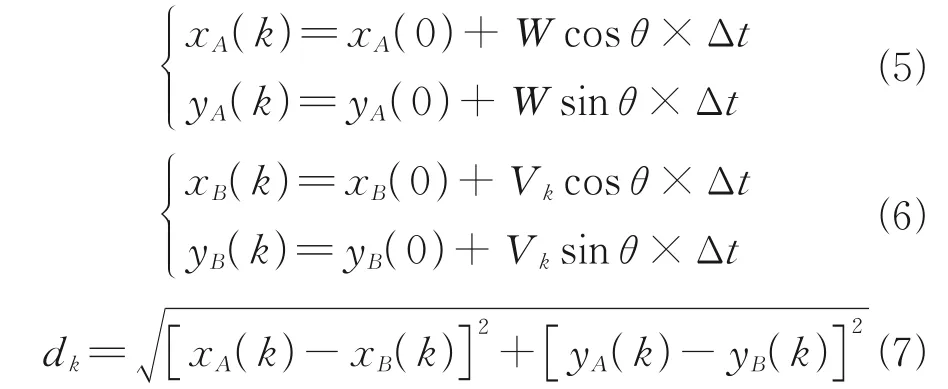
wherex(0) andy(0) represent the position of the aircraft at the initial time；x(k) andy(k) the position of the aircraft at statek；θis the included angle between the flight route and true north direction.

As for the separation allocation at pre-tactical stage， distance is the standard to judge whether the two aircraft have a potential conflict risk［25］. Therefore， the relative distance between the two aircraft is used as an index to judge the conflict. It is assumed that the designed aircraftAis fixed， and the relative coordinate system is established with the ownshipBas the origin. Thus， the position of the ownshipBbelow the relative coordinate system isThe coordinate transformation equation is as

Then the ownshipBflies along the straight line can be calculated as

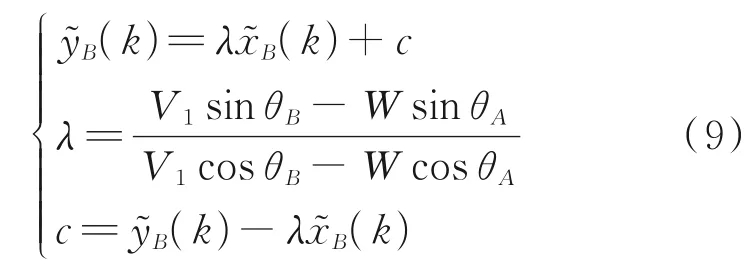
In the relative coordinate system， the conflict relationship between the two aircraft is transformed into the length between the shortest distanceLof the two aircraft and the safety separation

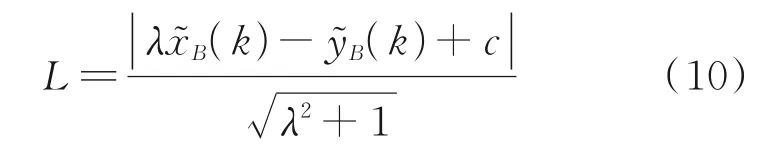
Fig.3 shows three positional relations between the shortest distance of two aircraft and the protection area of designed aircraft， under the relative coordinate system. IfL＜r， there is a conflict； ifL≥r， there is no conflict .

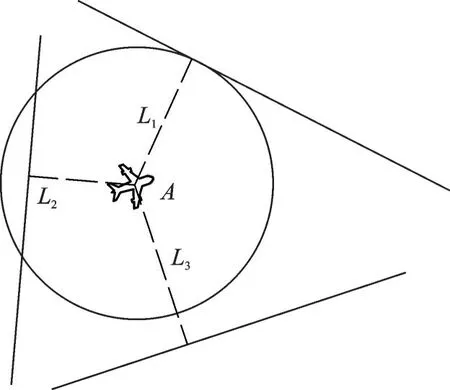
Fig.3 Positional relations of cross-conflict

With regard to the optimal separation allocation model for the cross-conflict scenario， as shown in Fig.4， the positions of the two aircraft are projected in the true north direction. That means we just consider the velocity component of the true north direction， which transforms the cross-conflict problem into the following conflict problem. And the velocity model proposed in the previous section is adopted to reallocate the safety separation of the two aircraft. Hence， the state equations of ownshipBand the designed aircraftAare

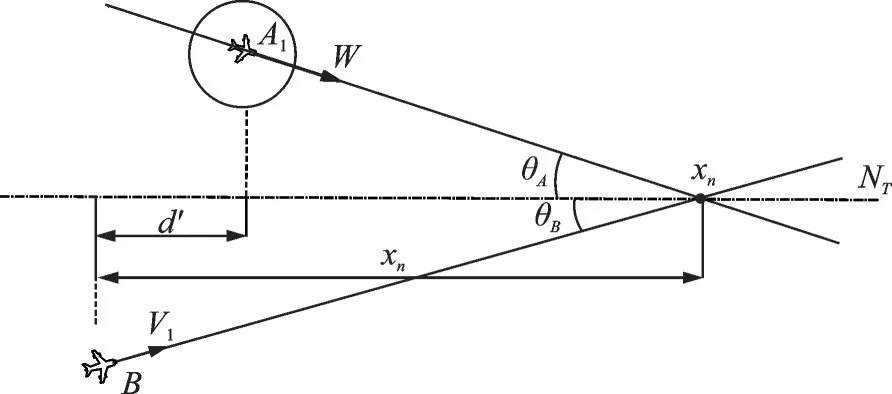
Fig.4 Separation projection of cross-conflict

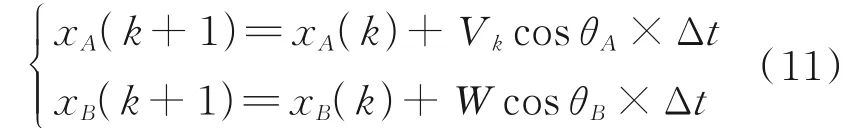
At timek， the projection of separationd′kbetween two aircraft can be calculated as

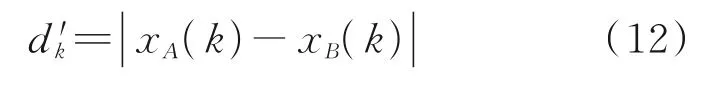
2 Optimal Control Algorithm

2.1 Dynamic programming algorithm

The optimal control problems of conflict free system generally involve a series of complex nonlinear differential equations， from which it is difficult to find the global optimal solution by traditional algorithms［26］. In this work， the dynamic programming algorithm is introduced to discretize the continuous system in the light of time characteristics［27］. The solving process is that the optimal return functionfk，n(xk) of each segment is gradually obtained from the terminal stage to the initial stage according to the constraints. In addition， since the initial state of the system is known， the optimal control law sequence can be calculated step by step from front to back by bringing in the optimal return function［28-30］. In virtue of the fact that the dynamic programming algorithm separates the current state from the states of future segments， in addition to combining the current and future benefits， the decision of each segment originates from the consideration of the current stage to the historical stage， and thus the global optimal solution can be obtained［31］.

According to the basis of dynamic programming， it has been concluded that the following requirements should be met for the establishment of the dynamic programming model：

（1） Divide the process intonsegments （generally in terms of time and space）.

（2） Determine the state variablexkthat has no aftereffect.

（3） Determine the control variableak.

（4） Determine the state transition equation

（5） Determine the return functionJk， which satisfies：

① A scalar function is defined on the whole process and all the preceding sub processes.

② The return function from stagekto stagensatisfies the recursive relationship

The best return function in stagekis

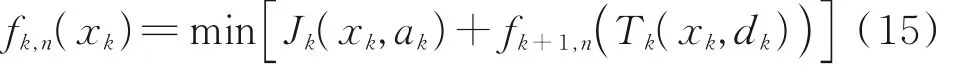
wherekrepresents the current stage；xkthe timevarying state variable of stagek；akthe control law of stagek；Jkthe return function of stagek；fk，nthe best return function of the later sub process of stagek.

According to the above conditions and combined with the time characteristics of the aircraft following model， the reverse sequence solution of dynamic programming is used to establish the optimal control model for the separation control［32］. The flight time of the ownship from the initial point to the terminal point is divided into stages， and its state number is given as

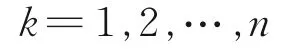
The initial state is given as

The end state is given as

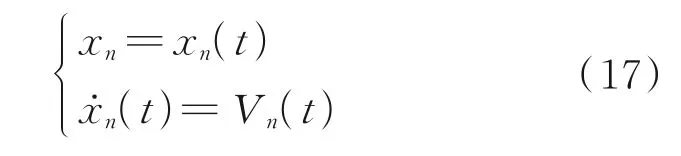
The state equations are given as

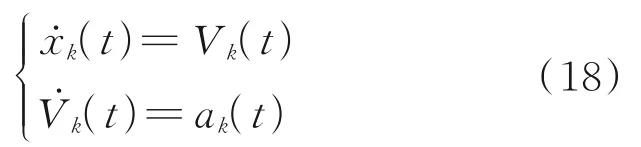
where the control lawak(t) of each sub-stage is a function of timet， hence the solution of the control law in this work is actually to solve the extreme function of each sub stage.

The constraint set is given as

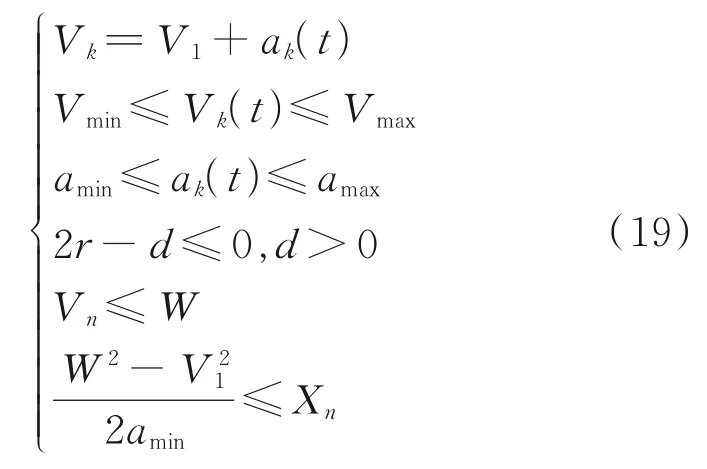
whereVmaxandVminare the upper and the lower bounds of the flight speed， respectively；amaxandaminare the upper and the lower bounds of the flight acceleration， respectively.

The revenue function of the end stage is defined as

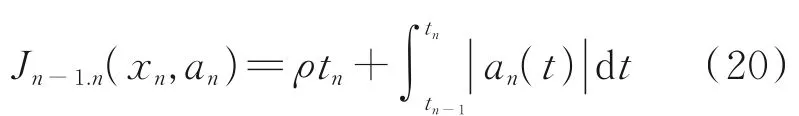
whereρis the time weighting coefficient， then the best return function in the end stage is given as

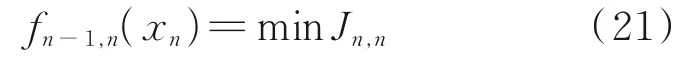
In this research， the sequential quadratic programming algorithm（see Section 2.2 for details） is introduced to calculate the optimal control lawand optimal return functionfn-1，n(xn) in stage （n-1） ton， and then the optimal control lawin stage （n-2） tonis determined.

The state transition equation satisfies

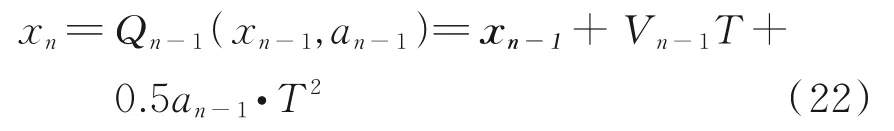
whereTis the time interval from stage (n-1) ton. The total return function from stage (n-2) tonis

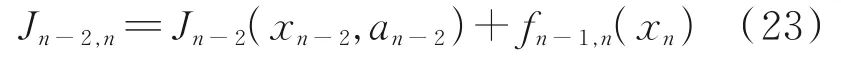
Based on Eqs.（17，18）， the optimal return function from (n-2) ton

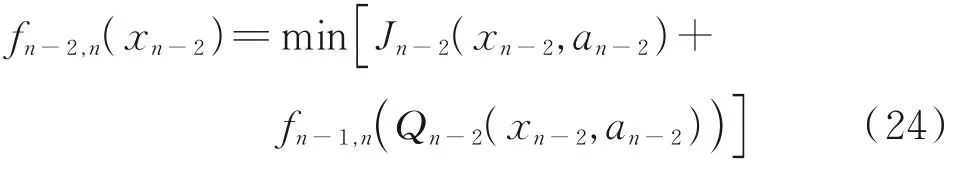
In this way， recursion is exerted step by step， until there is an optimal revenue function from the initial stage to the end stagen

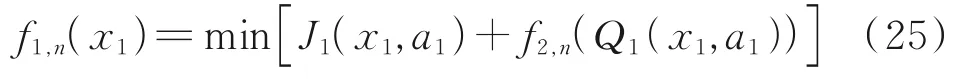
Substituing the initial statex1into Eq. （25）， we obtain the optimal control law sequencegradually from front to back.

2.2 Sequential quadratic programming algorithm

The dynamic programming algorithm only gives a set of necessary conditions for solving the optimal control problem， but it is difficult for the dynamic programming algorithm to obtain the analytical solution for the model with complex constraints. Therefore， in order to calculate the optimal return function and the optimal control law at each stage， this work can only search for a numerical solution. For the optimal control problem with the constrained control law， the mainstream numerical calculation methods include the interior-point penalty function algorithm and the sequential quadratic programming （SQP） algorithm.

Although the traditional interior-point penalty function method can deal with the optimal control problem with general inequality constraints， the Hessian matrix will deteriorate near the extreme point， which makes the calculations difficult to converge to a solution［33］. Therefore， SQP has been used to solve the optimal value for each stage， which has marked advantages in solving nonlinear functions with multivariable. This algorithm simulates Newton’s method while dealing with constrained optimization problems. In each main iteration， the augmented Lagrange multiplier has been introduced to bring the constraint into the return function， that is， the constrained optimal control problem was transformed into an unconstrained nonlinear extreme value problem， and the quasi-Newton method is used to approximate the Hessian matrix of the Lagrange function. Then the matrix is used to generate the sub-problem of quadratic programming. The solution constitutes the search direction of a 1D search process. The optimal control law is solved， and finally the optimal return function is obtained.

In regard of the above problems， the constraints are brought into the return function

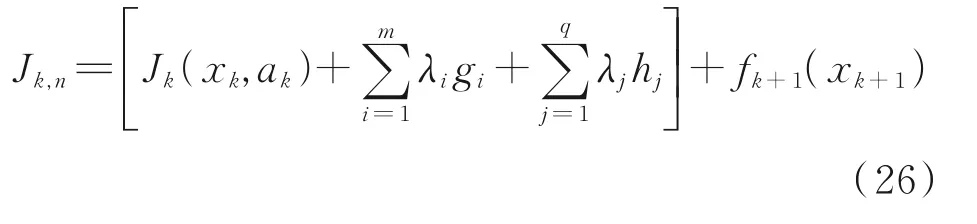
whereλirepresents the Lagrangian multiplier；giandhirepresent the inequality and equality constraints in Eq.（19）， respectively

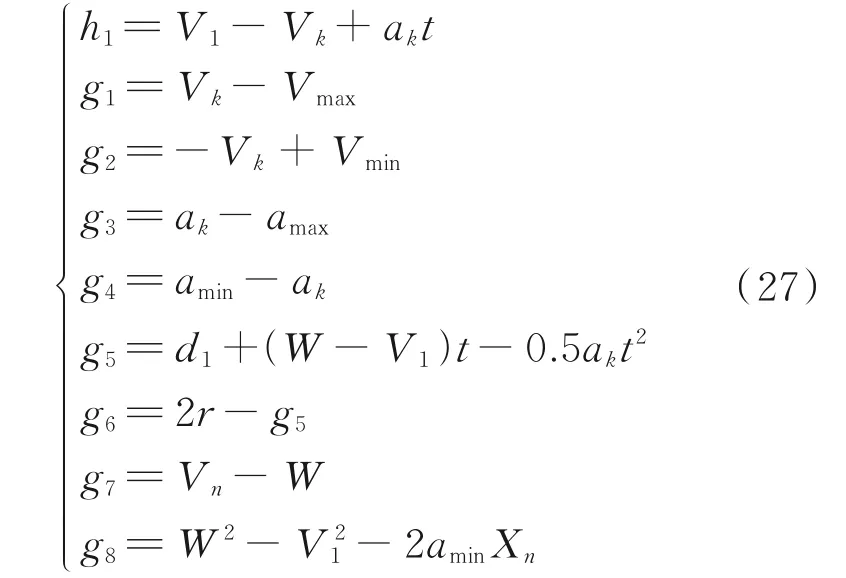
The Hessian matrix formula of the Lagrange equation is given as

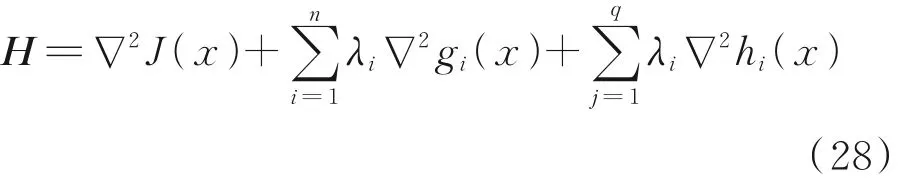
The iterative equation based on the Hessian matrix is given as

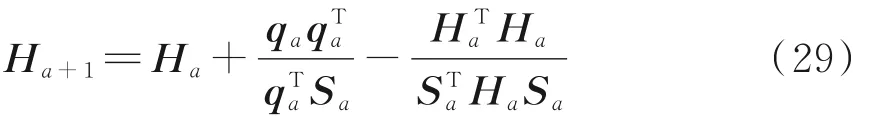
where

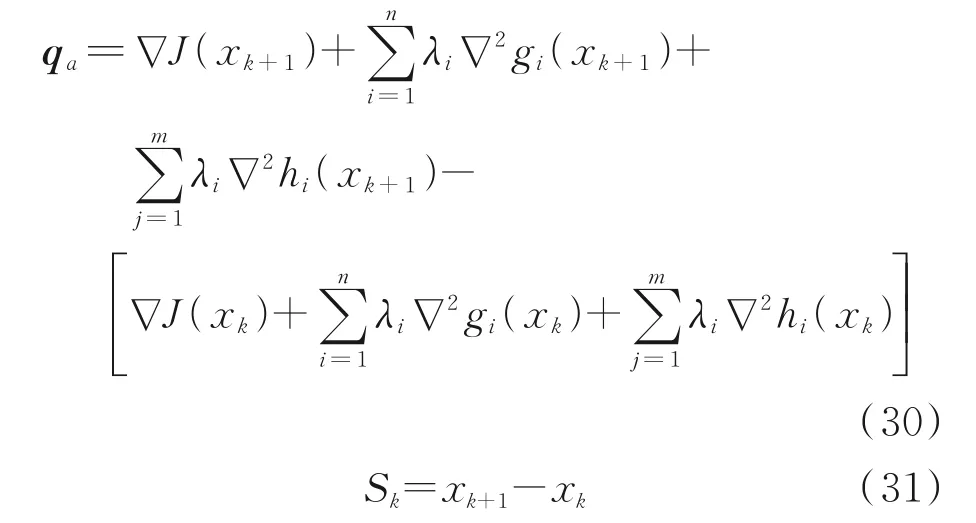
The specific steps of the algorithm are given as follows.

Algorithm： DP-SQP combined algorithm

Input：x1；xn；a0；t0；W；V1

Output：Jk，n，fk，n，a*k，tn，d，V

Initial= Set（x1；xn；a0；t0；r；W；V1；d1）

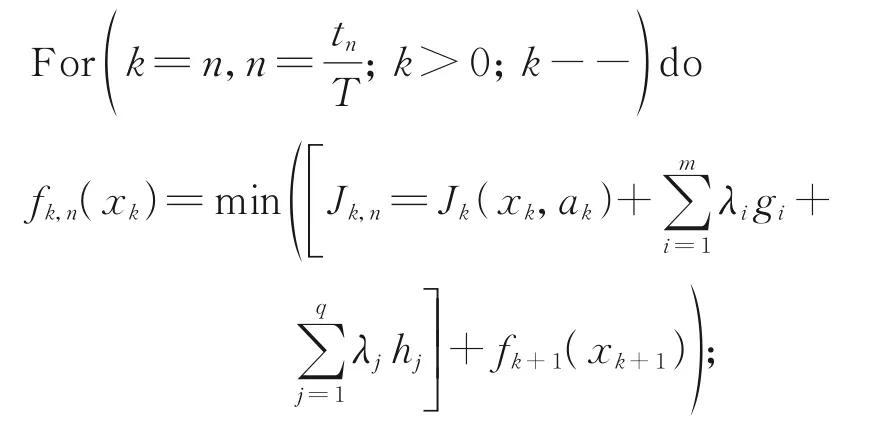
End for

For （k=1；k＜n；k++） do

Bringxkintofk，n(xk) and solve

End for

Final

According to the above pseudo code， when the dynamic programming algorithm meets the optimal substructure conditions， an optimal sub-tree containsnstates， and (n-1) times of extreme value functions need to be calculated. When calculating the optimal return function and optimal control law of each state， the sequential quadratic programming algorithm needs to be used for iteration， and its algorithm complexity isO(N). Therefore， the time complexity of the algorithm in this research can be expressed asO(N2).

Fig.5 shows the iterative curve of the optimal return function at the end distanceXn=30 km. Each stage of the iteration adopts the sequential quadratic programming algorithm to solve the optimal value. The iterative process of the return function is stable without oscillations and breakpoints.

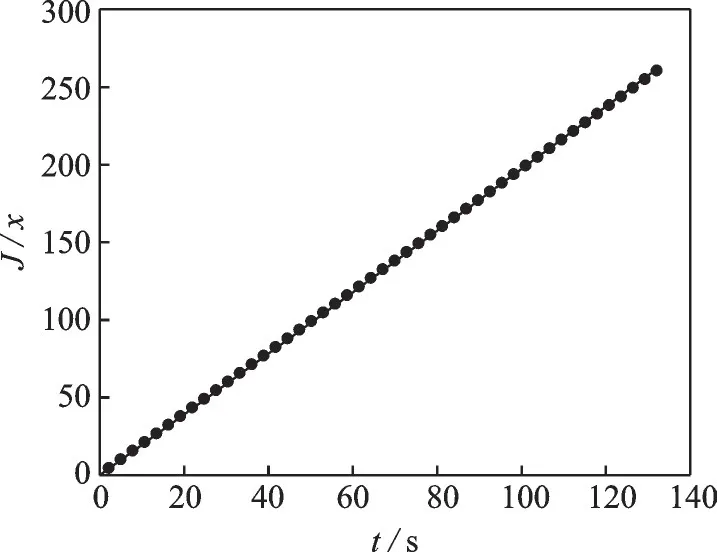
Fig.5 Objective function iterative curve

3 Verification of Separation Control Strategy

3.1 Algorithm feasibility verification

To verify the feasibility of the proposed combined algorithm， we adopt the following conflict model as a typical example， and simulateit by MATLAB. According to the aircraft kinematic constraints specified in Base of Aircraft Data （BADA）［34］documents， the selected model parameters are shown in Table 1. According to Eq.（5）， the minimum end distance is 19.17 km. Therefore， as shown in Table 1， this research designed six groups of following conflict cases to discuss the influence of diverse end distances on optimal separation allocation strategy. Compared with the traditional interior point method， the simulation results verify the superiority of this algorithm.

Table 1 Model parameters

Fig.6 shows the arrival time curves under different end distances. The blue asterisk and black rectangle mark the arrival time for the end point， which is calculated by the traditional interior point method and the combined algorithm， respectively. The red circle mark the estimated time of arrival （ETA） time of ownship， that is， the expected arrival time of ownship at the end point while maintaining the original flight speed. When the end distance isXn=20 km as can be seen from Fig.7， since the buffer distance for separation control is relatively short， it is necessary to adopt a larger control law to adjust the speed of ownship. Therefore， there is not much difference betweentnand ETA in this case. The buffer distance for the speed regulation of the ownship has been extended as the end distance has increased， and the arrival time delay caused by the speed regulation has gradually appeared. The time delay is positively correlated with the end distance， especially when the end distance exceeds 50 km. As shown in Fig.7， if the buffer distance is long enough， there is a lower limit to acceleration under the restrict of safety separation. After the ownship adjusts its speed to match that of the designed aircraft with the minimum acceleration， it can only continue to move at this speed until it reaches the end point. The simulation results show that on the premise of ensuring aircraft flight safety， the calculation results accord with the objective change law of implementing the separation control strategy.

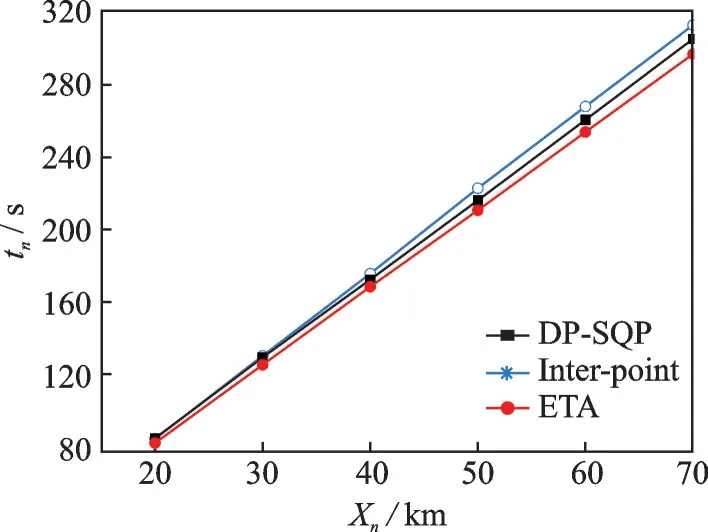
Fig.6 End time-end distance curves

Fig.7 Control law-end distance curves

Table 2 shows the comparison of simulation results between DP-SQP and the interior-point algorithm. It can be seen that the DP-SQP algorithm takes less time to reach the specified end point than the traditional interior-point method. And this advantage becomes more obvious as the end distance increases. The delay timetdis defined as the difference between the end point arrival timetnand ETA of the ownship. When the end distance isXn=20 km， the delay timetdof the two algorithms is almost the same. As the increase of the end distance， for instanceXn=70 km， the delay time of combined algorithm is only 54.52% of that of the interior-point method. In addition， while the maximum acceleration of the both algorithms reaches 0.4 m/s2under the condition ofXn=20 km， the combined algorithm has obvious advantages in solving the parameters such as the optimal arrival time and the optimal control law under the medium distance conditions.

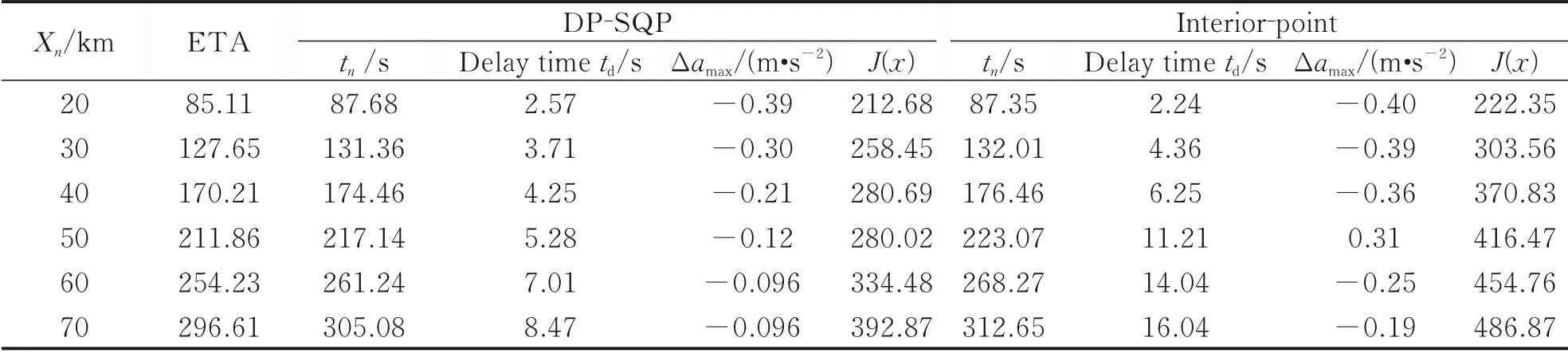
Table 2 Comparison of the results of two optimal control algorithms

In order to discuss the difference between the optimal separation allocation strategy of the two algorithms， Fig 8 shows acceleration curves of the two optimal control algorithms under the same enddistance conditions. From the acceleration curves， we can find that there are distinct differences between the two optimal control algorithms in terms of the separation control strategies. DP-SQP combined algorithm adjusts the speed with a small acceleration in the initial stage， and then gradually increases until the terminal stage， while the traditional interior point method adjusts the speed with the maximum acceleration in the initial stage of the separation control， and then gradually decreases until the end stage. Based on passenger comfort requirements and actual flight conditions， the speed regulation strategy of the combined algorithm will not cause a surge of speed in a short period of time， which is more reasonable.

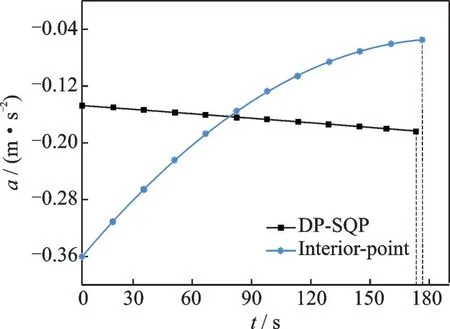
Fig.8 Comparison of two algorithms for optimal control law curves

3.2 Simulation of following conflict

The variation characteristics of the control law of the optimal separation allocation algorithm has been further investigated under different end distances. The separation allocation scenarios are set asXn=20 km，Xn=40 km andXn=60 km， which correspond to short distance， medium distance and long distance respectively. And the acceleration and speed curves of the ownship are discussed in the following conflict scenarios， as well as the variation law of the separation with time.

Figs.9， 10 are time-varying curves of the acceleration and the speed for the ownship corresponding to the three end distances. As shown in Fig.9， the acceleration of the ownship under every end distance shows a trend of growing with time， but the growth trend is more visible as the end distance increases， and the maximum acceleration is significantly negatively correlated with the terminal distance. In particular， forXn=60 km， the acceleration control of ownship does not last from initial time to end time. In the speed curves of Fig.10， it can be seen that when the ownship decelerates to 222 m/s （i.e. the same speed as designed aircraft）， it will continue to fly at a constant speed until it has passed the end point. Therefore， under the constraint of the safety distance， the ownship will adjust its speed from the initial speedV1toWat the minimum acceleration to ensure a safe flight. The final speed of ownship is reduced to 222 m/s whether the end distance is short， medium or long.

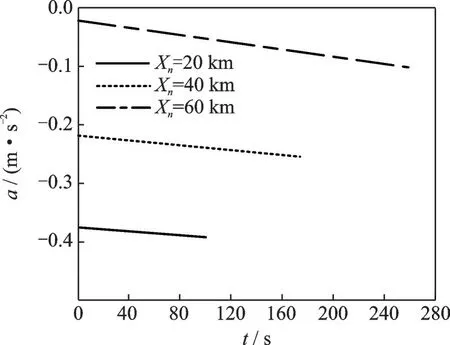
Fig.9 Control law curves with time under different end distances

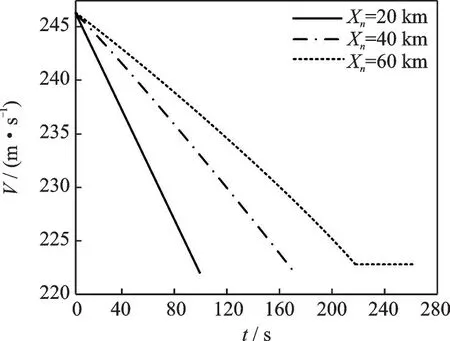
Fig.10 Speed variation curves with time under different end distances

As shown in Fig.11， the separation between two aircraft varies with time under different end distances. The comparison of the end distance conditions indicates all the separation curves reach 10 km at the end points， which is the minimum separation for pairs of aircraft to maintain a safe flight. Moreover， separation curves tend to be horizontal near the end point， which signifies that the speed of the ownship is almost the same as the designed aircraft near the end point. In addition， whenXn=60 km， the ownship keeps the minimum safety separation before reaching the end point. It shows that there exists a limit control law for the speed adjustment strategy under the constraint of the model constraint set. Therefore， when the ownship has been adjusted to the desired speed by the limit control law， the desired speed will be maintained until the terminal point is reached.

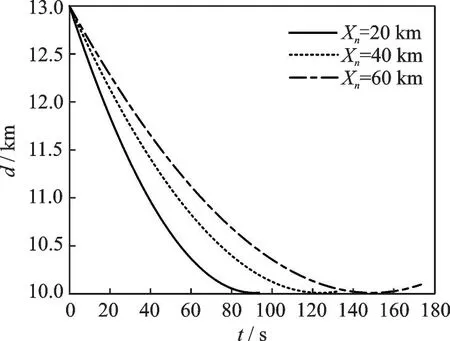
Fig.11 Variation curves of separation between two aircraft with time under different end distance conditions

If the number of separation control statenis too small， it will affect the reliability of the simulation results； on the contrary， ifnare too large， it will increase the unnecessary calculation quantity. Table 3 shows the numerical results for differentnvalues. We can find that the calculation results tended to be stable atn=100. Considering the efficiency of numerical calculation and the accuracy of results， this work selectsn=100 as the number of interval control process.

Table 3 n-value independence verification

3.3 Simulation of cross-conflict

This section analyzes the availability of the crossing separation allocation model in the actual operation environment under different included angle of air routes.θA=30° is set as the angle between the route of the designed aircraft and the true north direction. The included angle between the route of the ownship and the true north direction is represented byθB. The control variable is introduced for describing the relevant data of the cross-conflict model. Three groups of cross-conflict simulation with included anglesθB=0°，θB=15°，θB=30°（corresponding to the cross-conflict scenarios where the cross angles is 30°， 45° and 60°， respectively） are performed. The simulation parameters are summarized in Table 4. Like the simulation of aircraft following model， the selection of kinematic parameters is shown in Table 1. Given the end distanceXn=40 km， the relevance between the optimal control law and the included angle of the route are verified by the cross-conflict simulation.

Table 4 Simulation parameters

In order to verify the separation allocation algorithm of the cross-conflict， as shown in Fig.12， acceleration of the ownship is used as the control law to solve the optimal separation adjustment strategy under different included angles. It can be seen that the ownship faces a greater loss of speed with the increase of the included angleθBbetween the ownship route and the true north direction， caused by the projection of the local aircraft， which directly reduces the severity of the conflict. Therefore， whenθBis large， a relatively minor acceleration is required for speed adjustment to effectively avoid conflicts. The curves of the projection separationd′and the actual separationdof the pairs of aircraft are shown in Figs.13，14， respectively.

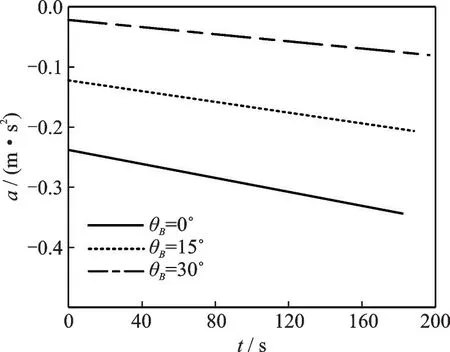
Fig.12 Control law curves with time under different included angles

It can be seen from the projection separation curves of the pairs of aircraft that the projection separation can eventually converge to the minimum safety separation under various cross angles. From Fig.14， it can be concluded that the actual separation curves start to rise after reaching the minimum safety separation， and the minimum value of the actual separation is within the safety range. In addition， although the combined algorithm does not maintain the actual separation at the minimum safety separation， it can still avoid potential conflicts effectively. It can be concluded that this algorithm can adapt to cross-conflicts with various included angles， but it has more obvious advantages in resolving conflicts with a larger included angle.

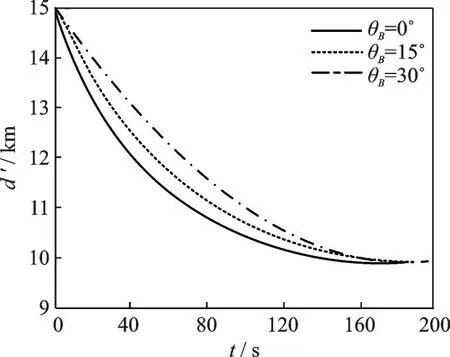
Fig.13 Projection separation curves with time under different included angles

Fig.14 Actual separation curves with time under different included angles

4 Conclusions

The optimal separation allocation problem of a continuous system based on 4D flight trajectories has been transformed into a class of multi-stage optimal policy decision problems.

（1） With regard to aircraft flying along 4D mensional trajectoryies， a conflict detection model based on the conflict protection area is proposed， and on this basis， the aircraft-following model and the cross-conflict model are established to mathematically describe the movement of pairs of aircraft in the conflict process.

（2） A DP-SQP combined optimization algorithm is proposed to adopt the speed adjustment strategy. The combined algorithm is used to optimize the multi-objective function for the shortest time delay and the minimum control law adjustment of the ownship. Comparative simulative analysis of the combined algorithm and the traditional algorithm has been conducted， and the results show that the combined algorithm has obvious superiority.

（3） The relationships between the end distance and the following separation allocation strategy， as well as the relationships between the included angle and the cross separation allocation strategy are discussed. Results from the simulated cases show that the the following separation allocation strategy and the cross separation allocation strategy can avoid potential conflicts effectively. In addition， the separation allocation strategy has a better result in case of a medium distance and a large included angle.

In this work， only the pairs of aircraft conflict scenarios have been studied. Future work will address the problem of separation allocation under the conditions of multi-aircraft following and cross-conflicts.