Path Planning for Lunar Surface Robots Based on Improved Ant Colony Algorithm
2022-02-10,,,,*
,,,,*
1. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, P. R. China;
2. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, P. R. China
Abstract: In the real-world situation, the lunar missions’ scale and terrain are different according to various operational regions or worksheets, which requests a more flexible and efficient algorithm to generate task paths. A multi-scale ant colony planning method for the lunar robot is designed to meet the requirements of large scale and complex terrain in lunar space. In the algorithm, the actual lunar surface image is meshed into a gird map, the path planning algorithm is modeled on it, and then the actual path is projected to the original lunar surface and mission. The classical ant colony planning algorithm is rewritten utilizing a multi-scale method to address the diverse task problem. Moreover, the path smoothness is also considered to reduce the magnitude of the steering angle. Finally, several typical conditions to verify the efficiency and feasibility of the proposed algorithm are presented.
Key words:ant colony algorithm; grid map; multi scale; path smoothing
0 Introduction
Lunar base construction and resource development is an important aspect of expanding the human playground in the future. The lunar surface robot will be a critical assistance and vital tool for astronauts to develop and utilize lunar resources. Lunar robot task allocation and path planning will be largescale planning problems, with the increasing number of robots. The uncertainty of path planning application scenarios and terrain conditions has further increased based on the improved robot performance and expanded planning scale. Diverse planning situation requires searching algorithms having the flexibility to adapt to various scales and high computing efficiency to fit complex terrain. Therefore, it is particularly critical to plan a short, safe and smooth path for robots to reach the target position on the lunar surface.
In-depth research on path planning has been carried out for decades, which can be divided into two types, one is based on the theoretical model, and the other is based on the random search algorithm. In terms of random search-based planning methods, Li[1]proposed an improved method for the A* algorithm. This method combines the AGV state with the fuzzy logic rules as the heuristic information and dynamically adjusts the heuristic function weight. Alireza et al.[2]enhanced the mutated cuckoo optimization algorithm (MCOA) which has the ability to deal with several unmapped objects and takes less time than the GA and A* algorithm. A new genetic algorithm with higher efficiency than A* algorithm on larger scale, based on the path network, was proposed by Li et al[3]. To enhance the calculating efficiency and reduce the number of nodes, a combination algorithm of probabilistic roadmap algorithm (PRM) and probability-based bidirectional rapidly-exploring random trees (P-Bi-RRT) was discussed by Xu et al[4].
The ant colony algorithm is widely used in searching for the optimal path due to its stability and reliability. By imitating ants’ foraging behavior, the ant colony algorithm promotes optimization ability on intelligence, efficiency, accuracy, and application scope. Compared with the A* algorithm, GA algorithm, and other random search algorithms, the ant colony algorithm has positive feedback, and the algorithm can adopt distributed computing framework and heuristic probabilistic search method, making it easier and more efficient to find the global optimal solution. So, the ant colony algorithm is widely used to solve path planning problems. A fusion method of the segment and global path planning was proposed by Shi et al[5], which searched globally utilizing the potential ant colony algorithm and locally with the improved artificial potential field (APF) method. The article by Chen et al.[6]suggested that the ant colony optimization algorithm can solve the unmanned aerial vehicle (UAV) path planning problem with outstanding robustness and scalability. Based on the ant colony algorithm, Zhao et al.[7]improved the calculating efficiency through increasing the adaptive adjustment into heuristic function. Shao et al.[8]suggested that setting a dynamical limit of pheromone’s attenuation coefficient can enhance the searching efficiency and reduce the probability of local optimal solution. Whereas, for the large-scale path planning problem of complex terrain, the current ant colony algorithm remains problems of searching blindly in the initial stage and having limits in searching scale.
A multi-scale improved ant colony algorithm is proposed in this paper, combined with the smoothness method for lunar robot intelligent path planning to adapt to the large-scale and complex lunar surface, hence the path searching efficiency, algorithm adaptation flexibility, and path safety are enhanced. The proposed algorithm can adapt various searchscale, reduce the probability of local optimum and enhance the convergence efficiency. Compared with the present method, there are three main contributions in this paper:
(1) Map the global space matrix into a new matrix with corresponding terrain complexity to enhance the searching scale of the ant colony algorithm;
(2) Propose a multi-scale method to escape from the local optimization quickly;
(3) Suggest that the ant colony algorithm can meet the requirements of large-scale and complex terrain on the lunar surface.
The paper is organized as follows. The basic idea of the multi-scale ant colony model is introduced in Section 1. Section 2 describes the algorithm design of the multi-scale ant colony model in detail. In Section 3, the proposed algorithm is used for lunar surface path planning, and the results are compared with the results obtained by the A* algorithm to illustrate the effectiveness of the multi-scale ant colony algorithm. Finally, some conclusions are drawn in Section 4.
1 Problem Description
(1) Symbol design
To explain the path planning problem, a simple mathematical model is designed,as shown in Fig.1.

Fig.1 Mathematical model
In coordinateXOY, path nodes are denoted as a set Node={nodei}, nodeiis theith node and nodei={nodexi,nodeyi}, where nodexiand nodeyiare nodei’s position. The first node node0is also denoted asS, and the last one nodenis also denoted asT, wherendenotes the last number of nodes.
Path segments between adjacent nodes are denoted as a setRt={Rtij}, whereRtijis the path segment between theith node and thejth one. Herej=i+1, 0≤i<n.
Path segment angle is denoted as a set Ang={θi},θ∈[0,π), whereθiis the steeling angle betweenRtijand prolonged line ofRt(i-1)i.
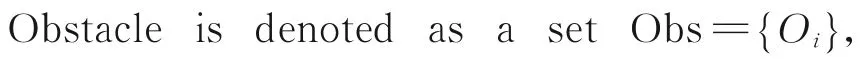
whereOiis theith obstacle.Oiis denoted as a thirdtuple setOi={Oxi,Oyi,ROi}, whereOxiandOyiareOi’s position,andROiis the length ofOi’s side.
The searching space isRsearch.
TheRsearch’s mean altitude isARand lunar robot’s motion has an altitude limit ofAlim.
(2) Path planning model
The lunar robot path planning problem can be defined as searching for an optimal or best path fromStoT, as shown in Fig.2. Path planning model can be described byS,T,Rt,Ang,Obs, and so on.

Fig.2 Lunar surface path planning
Obstacle avoidance model is

whereOxnandOynis the nearest obstacle to nodei.
The issue of path planning is to search for a shorter smoothing path with less calculating timetcalcuand smaller average steeling angle
The lunar space environment model is assumed as follows:
(i) If the altitude of positionA<AR-AlimorA>AR+Alim, the position is defined as an obstacle.
(ii) The lunar image is meshed into a grid map with different scales. The grid map is denoted as a matrixL, and it’s elementLijis 0 or 1, where 0 means passable and 1 impassable, according to the results of assumption (i). In this way,Rsearchis turned into a matrixL.
The mapping process is shown in Fig.3.

Fig.3 Lunar surface information processing
The classical ant colony algorithm has the disadvantage of low searching efficiency in the initial stage, especially in large spaces. Since the region scale of the lunar task could be large,Lmight contain a great number of elements. The ant pheromone parameterτis difficult to spread into the whole space in several periods with huge calculating amounts. Hence, the calculation efficiency is significantly reduced in large scale problems. Changing the number of elements in the initial matrix and narrowing down the searching range are utilized in the algorithm to reduce the influence of the scale.
Before the path planning, map every bunch of elementsh×hinto one element. In other words, split the initial matrixLinto a set of matricesLsmalland integrate each matrix as an element in new matrixLNew.Lsmall_mis themth matrix inLsmall,which corresponds withLNew_m, themth element inLNew.The matrixLNewconsists of new elements with terrain complexity TC, which is indicated with different grey levels, as shown in Fig.4. The start pointSand target pointTare also mapped inLNew.
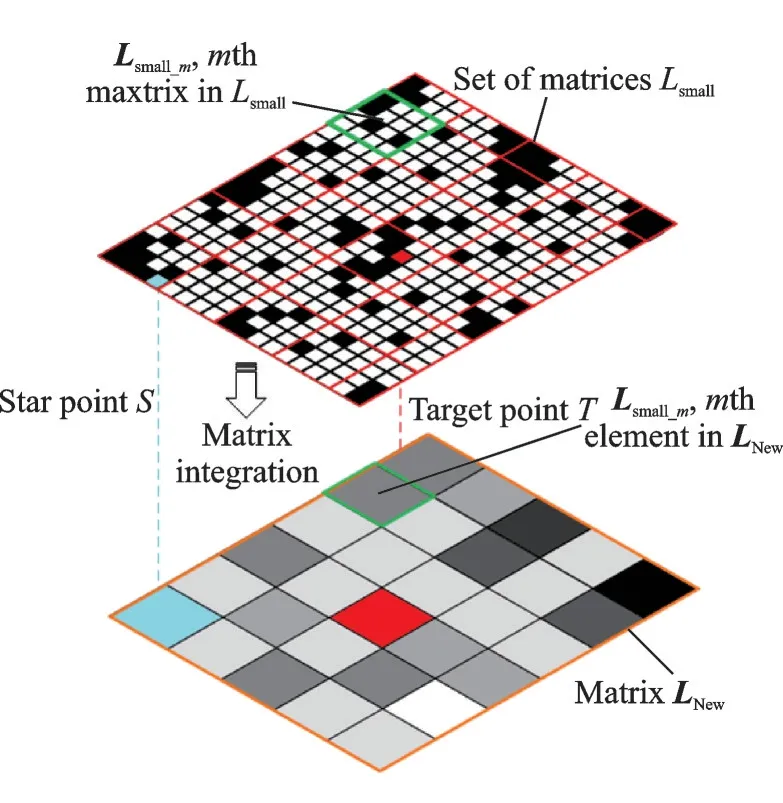
Fig.4 Matrix integration
Plan the path with a new matrixLNewand let passing elements map into the initial matrix to find the passing matricesLpassinLsmall. Plan pathRt_smallwith the passing matricesLpass, combine them with each other in turn, and grow into the initial pathRt, as shown in Fig.5.
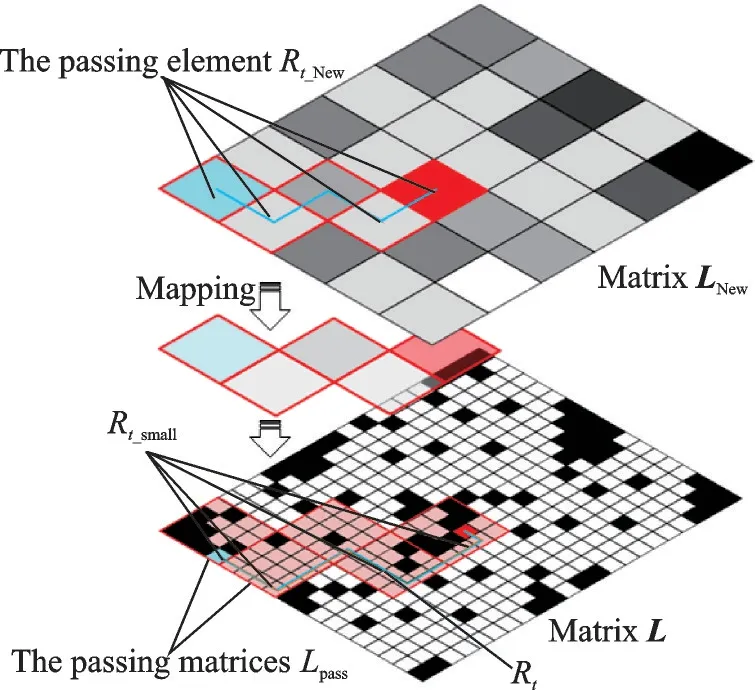
Fig.5 Illustration of mapping new matrix into initial matrix
The initial pathRtis remained to be optimized using ant colony algorithm. Firstly, collect path segmentRt_segby means of stochastic method and get the corresponding matrixMNew. Next, optimize the pathRt_seginMNewwithout changing the start point and end point, then get the result of optimizationRt_New. Finally, replaceRt_segwithRt_Newand update the pathRtwith local optimization mentioned above, as shown in Fig.6.
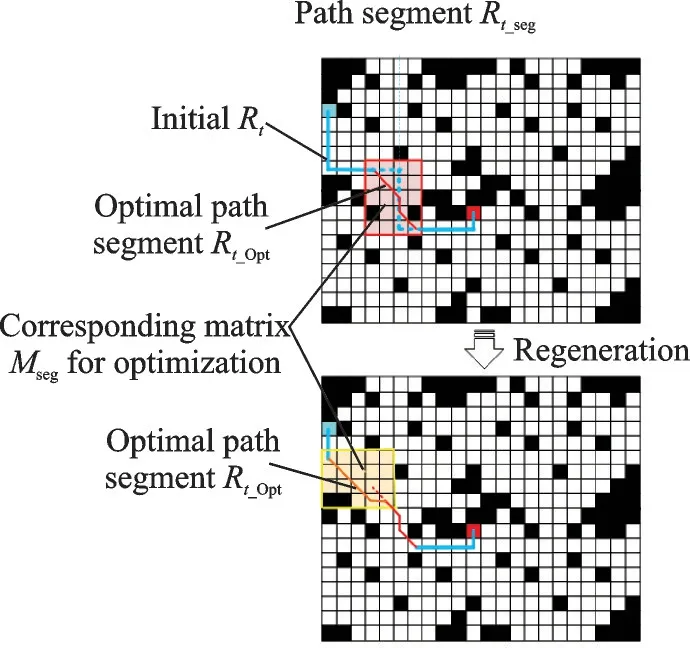
Fig.6 Path optimization
The actual lunar robot cannot drive on a polyline path; hence the path generated in the grid map is remained to be smoothed. The algorithm completes the smoothness control utilizing curve smoothing method, and the feasibility and efficiency of the final path are improved with the smoothing process, as shown in Fig.7.
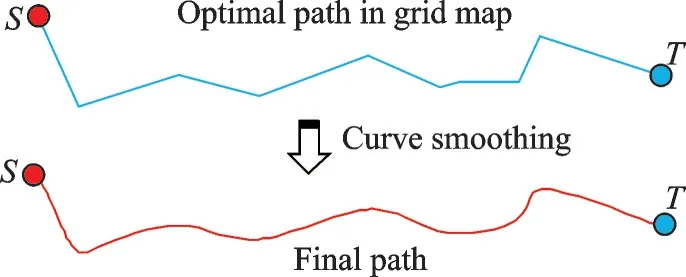
Fig.7 Path smoothing
2 Algorithm Design
2.1 Image process
First, convert the colored moon image into a grayscale picture, then obtain the picture’s pixels to gain a gray value matrix for each pixel MG. Calculate the mean pixels’ value meanrgbwhich reflects as mean altitude. Regard meanrgbas a pixel reference value and set value proportion rangeprgb. Finally, generate the global matrixL={lrc}, wherelrcis an element in therth row and thecth column. According to the assumption of the lunar surface environment, the global matrix can be defined as
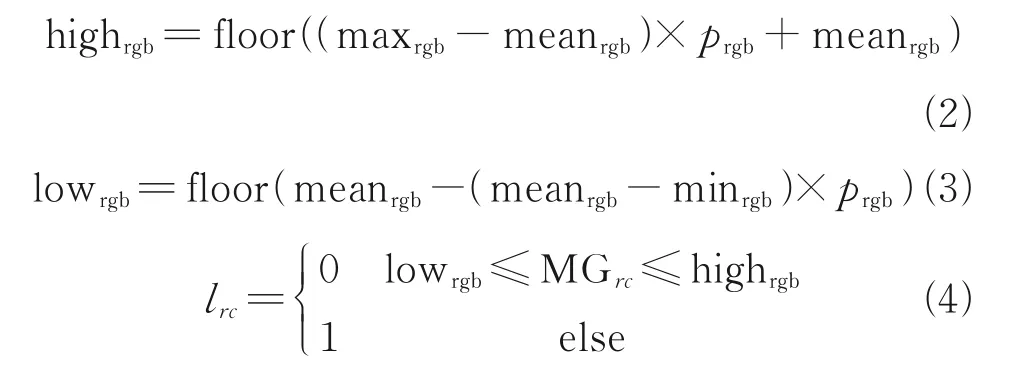
where 0 means accessible and 1 inaccessible; maxrgband minrgbindicate the maximum and minimum value in MG,respectively; highrgband lowrgbrespectively mean the upper and lower boundary in MG, corresponding toprgb. floor(A) rounds the elements ofAto the nearest integer less than or equal toA.
2.2 Improved ant colony algorithm
Express the heuristic functionηij(t) is in inverse proportion to the distance from next nodejto the target[9].
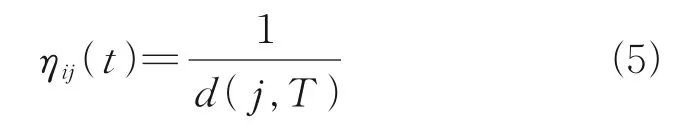
Set the lower limit ofτijto simulate the error probability in ant colony and increase the searching diversity.

Mortify the recording of pheromone[10-11]. Only record pheromone of ants which have reachedT, and the collection of these ants in thetth generation is arrivet,T.kdenotes thekth ant in arrivet,T. HereLkdenotes the length of the path taken by thekth ant in arrivet,T.
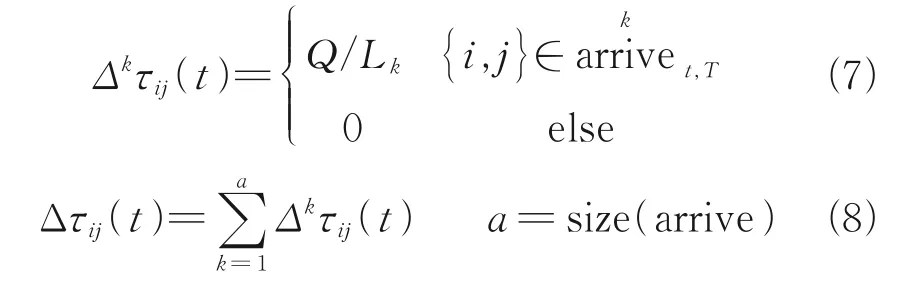
In traditional ant colony algorithm, the value of pheromone is assumed to degrade in each iteration. However, the main idea of the improved ant colony algorithm is to select path segment randomly for optimization, so as to obtain the global optimization result. Due to this randomness, this assumption is not applicable to the improved ant colony algorithm.
2.3 Path mapping method
The path mapping method is adopted to generate the initial solution, which enhances the calculation efficiency. The general idea is splitting global grid into several small bunch of matricesLsmall, and mapping each matrix ofLsmallinto each element in matrixLNewwith terrain complexity TC. After generating the optimal pathRt_NewinLNew, map the corresponding matricesLpassand combine the optimal pathRt_smallwith each other in turn, then generate the initial pathRt.
The regional splitting process is as follows:
(1) Confirm the number of elementsM1×M2inL.
(2) Set the number of elementsh×hinLsmall_m.
(3) SplitLintomatrices inLsmall. ceil(A) rounds the elements ofAto the nearest integer greater than or equal toA.
(4) The matrixLNewconsist of new elements, and each element takes value in [0,1]. The mapping relationship between the elements inLNewand the matrix inLsmallis reflected by TC, start pointSand target pointT.
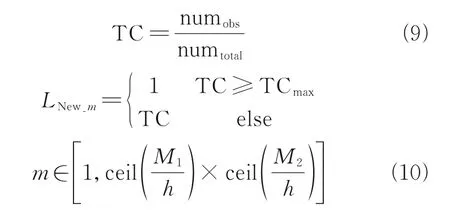
where numobsis the obstacle number inLsmall’s matrix and numtotalthe total number of grids inLsmall’s matrix.
Cancel the ant motion degree of freedom(DOF) of the upper left, lower left, upper right and lower right during the process of generatingRt_NewinLNew, to ensure the existence of accessible path between neighbor matrices inLsmall. Then, map theRt_Newnodes into matricesLpass.
The mapping method of generatingRtfromStoTinLis indicated as below.
(1) Iterate every pair of neighbor matrices inLpassand select accessible path between neighbor matrices.Lpass_nandLpass_mmean the upper and later matrix inLpass.JnandJmare the connected edge collections inLpass_nandLpass_m.

(2) SelectJnm’s elements, whose values are 0, intoJnm0as accessible collection. Select the posth elementsJposinJnm0by means of stochastic method. The target position inLpass_nisTpass_n,Tpass_n=Jn∩Jpos, and the start position inLpass_misSpass_m,Spass_m=Jm∩Jpos.
(3) Calculate the start position and the target in everyLpass’s matrix, according to the processes (1) and (2).
(4) Generate path inLpass’s matrix, and splice the path one by one. Then, obtainRtin global matrixL, as shown in Fig.8.
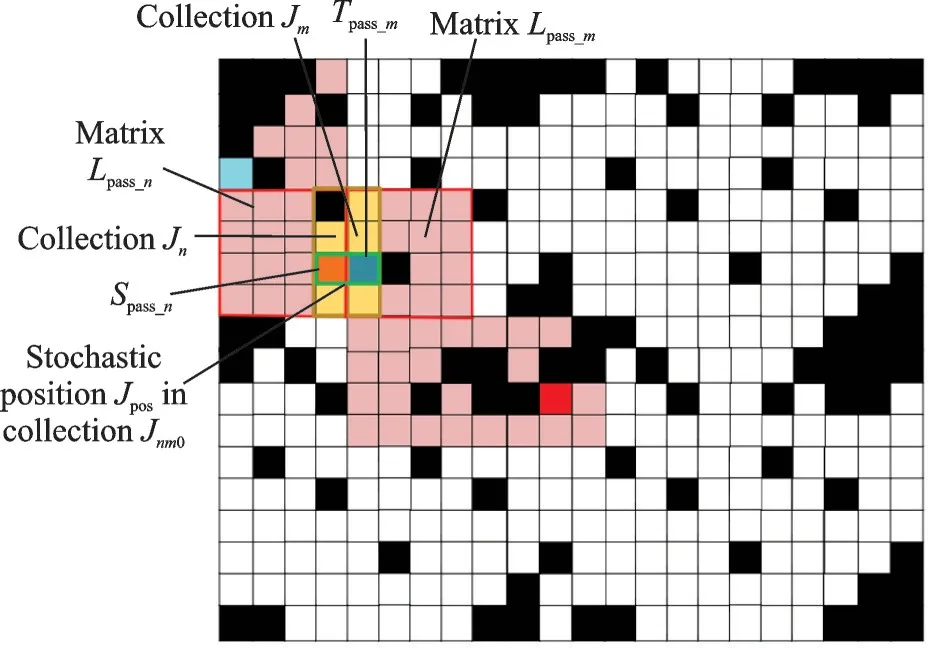
Fig.8 Searching start point and target in local matrix
2.4 Space splitting optimal method
The space splitting optimal method can optimizeRtwith stochastic method, reduce the probability of local optimal solution, and enhance the calculation efficiency. The overall process of space splitting optimal method is indicated as below.
(1) Set parameters of path segment optimization:Onumis the number of optimization,Pmax(0<Pmax<1) the upper boundary of segment-to-Rtratio;Pmin(0<Pmin<Pmax) lower boundary of segment-to-Rtratio;NOpt0the initial number of generations;MOpt0the initial number of ants in the algorithm.
(2) Search the start positionSOptin regional optimization, and determine the number of intercept nodes num. Then gain the certain path segmentRt_Seg.num=max[floor(((Onum-Oi)×Pmax×
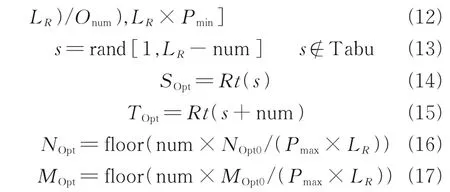
where rand[a,b] can generate random number fromatob; max[a,b] means selecting maximum one fromaandb;LRis the number ofRt’s nodes;TOptthe end nodes inRt_Seg;NOptthe current regional optimization ant colony iterate times;MOptthe number of ants.
Tabu list is set in this step within the process of regional path optimization. And the usedSOptposition is recorded in the tabu list, Tabu={Ssmall(1),Ssmall(2),…,Ssmall(Nsmall)}. If the new start position is already in Tabu, then reselect.
(3) Get the corresponding matrixMSegtoRt_Seg. Iterate every node inRt_Segand find the maximum and minimum value inx-axis andy-axis. ObtainMSegaccording to the maximum and minimum value mentioned above. Path planning is implemented inMSegto obtain the solutionRt_Opt.
(4) ReplaceRt_OptwithRt_Segand update the pathRtwith local optimization mentioned above.
(5) Repeat Steps (2—4) until reachOnum.
2.5 Path smoothing process
After path mapping and space splitting method, obtain Node={nodei} which needs to be smoothed. This work adopts the smoothing method proposed by Refs.[12-14] to reduce the magnitude of the steering angle and improve path safety.
The definition of weight functionw(x) is described as
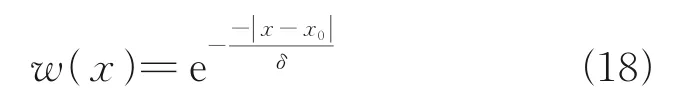
whereδis the smoothing factor.
While calculating the nodek’s new position, select 2mpoints around nodekas the smoothing collection and establish a local coordinate system centered on nodek.
Control the smoothness of the curve through parameters, set the nodei’s parameter asti. Then the parameterization of nodei={nodexi,nodeyi} generates two components in theXandYdirections: (ti,nodexi) and (ti,nodeyi).
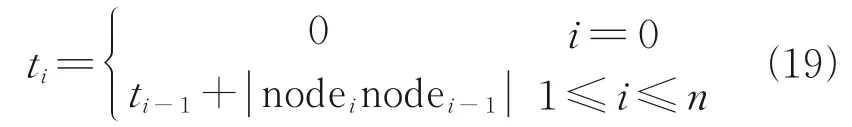
Set the parameter of farthest node astjand the weight asα. Then obtain the initial smoothness factorδ0.
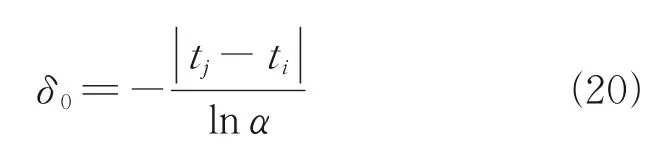
Calculate nodei’s weight matrixWaccording to the function (18) andδ0.

The nodei’s new component in theXdirection isx′i=axand the new component in theYdirection isy′i=ay. So the new position nodei=(x′i,y′i).
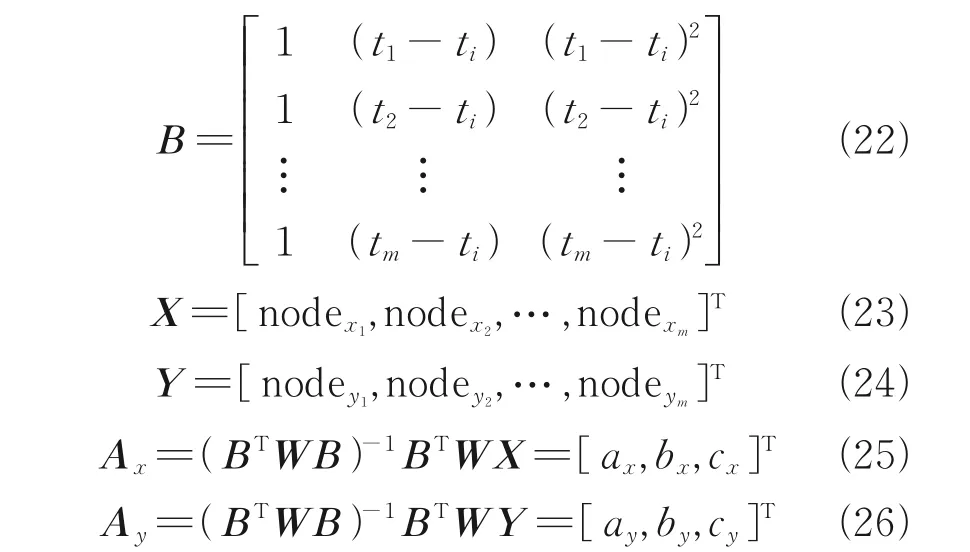
Smooth residualdiis used to denote the distance between the original position nodei={nodexi,nodeyi} and the new position nodei=(x′i,y′i). To ensure nodes are still in the original grid, select the node nodekwith the maximum smooth residualdkand suppressdkwithin 0.5 by decreasing the value ofδ.
3 Simulation and Result Analysis
The lunar surface image is shown in Fig.9.Transfer Fig.9 into grid mapL, which contains 658×800 elements. Then, splitLintoLsmall’s matrices. (a) denotes matrices’ scale inLsmallis 50×50 and (b) matrices’ scale inLsmallis 20×20, in Figs.10—15.

Fig.9 Lunar surface
Set TCmax=0.4 and the grid level is proportional toLNew_m’s value. The path planning parameters inLNeware:N=30,M=60,τmin=0.1. The start position inLis at the 150th row and the 1st column and the target at the 350th row and the 375th column, as shown in Fig.11.
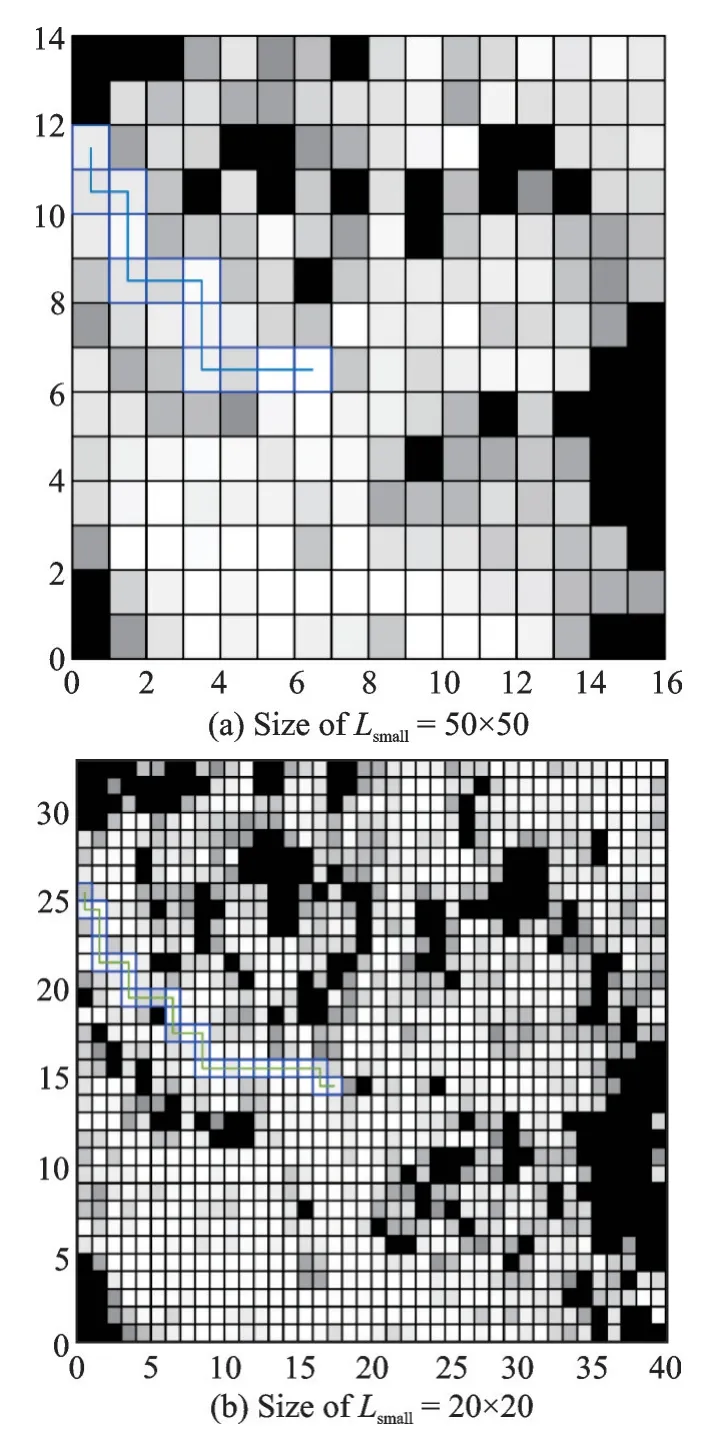
Fig.11 New matrix
The path planning parameters inLpassare:N=10,M=50, andτmin=0.1.The initial pathRtis shown in Fig.12.

Fig.10 Split grid map

Fig.12 Initial path
The regional optimization parametes are set as:Onum=200,Pmax=0.085,Pmin=0.05,Nsmall0=60,Msmall0=50, and the other constant parameters are the same as those inLpass.The relationship between the path length and the regional optimization number is shown in Fig.13.
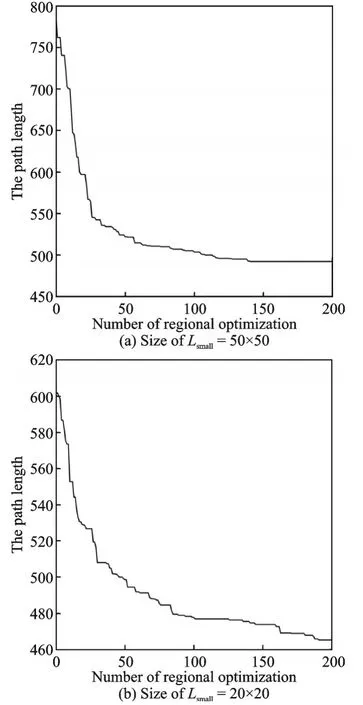
Fig.13 Relationship between the path length and optimization times
The optimal path before smoothing method is shown in Fig.14, where mean steering angle=14.408 867 and the number of large angles is 122. This work regards steering angle bigger than 20° as large angle, as shown in Fig.14.
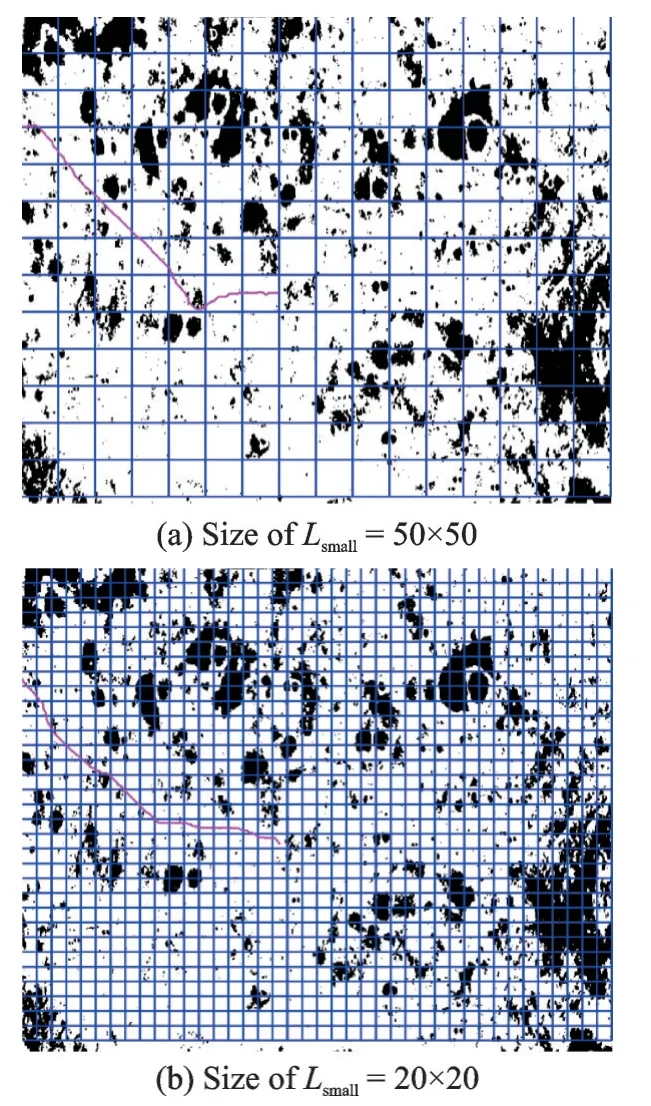
Fig.14 Optimal path before smoothing method
After path smoothing process,=1.981 138 and the number of large angles is 0, as shown in Fig.15.
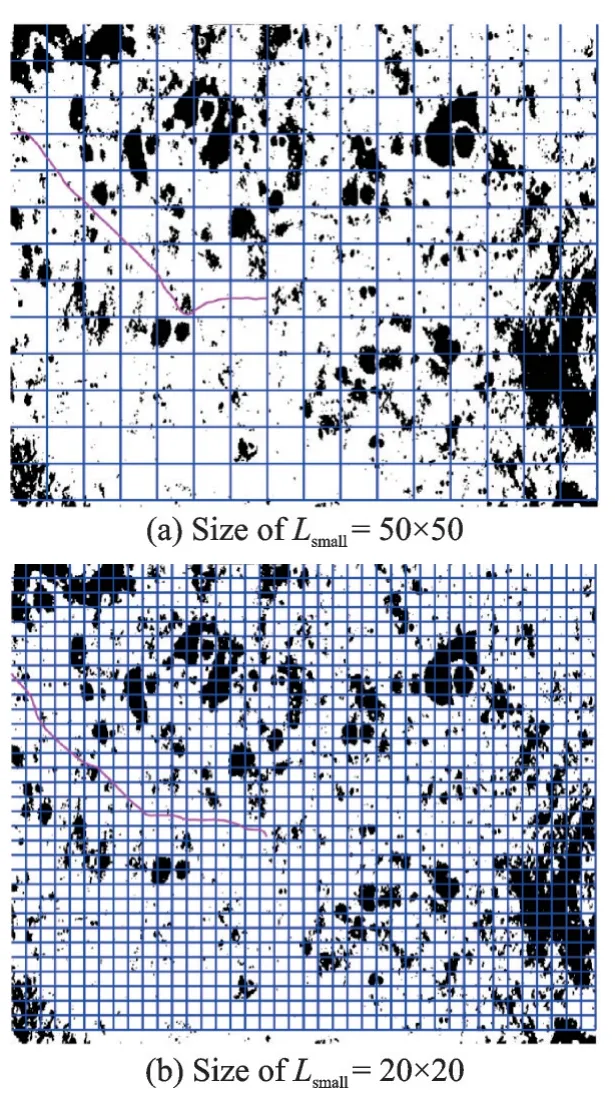
Fig.15 Final optimal path
The size ofLsmallin the path mapping method is an adjustable parameter that should be determined according to the task. In this scenario, the other parameters are the same as those mentioned above.
The size ofLsmallis given from 15×15 to 50×50. The average results after removing the highest and lowest values in 8 groups of simulation are shown in Figs.16—21.
From the experimental data, the computing time of generating the path inLNewis in inverse proportion to the size ofLsmall, and the computing time of generating the initial path inLpassis in proportion to the size ofLsmall. The total computing time has minimum value when the size ofLsmallis 19×19.
The relationship between the size ofLsmalland the computing time by space splitting optimal method is as follows.
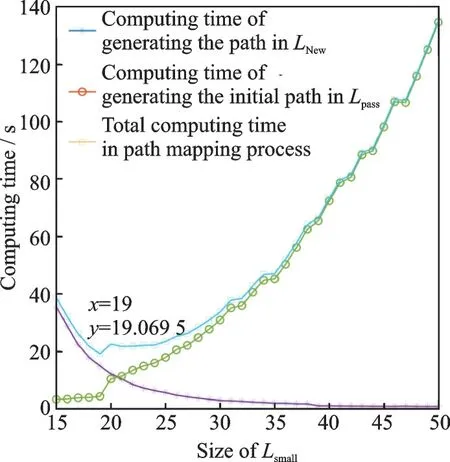
Fig.16 Relationship between the size of Lsmall and computing time by path mapping method
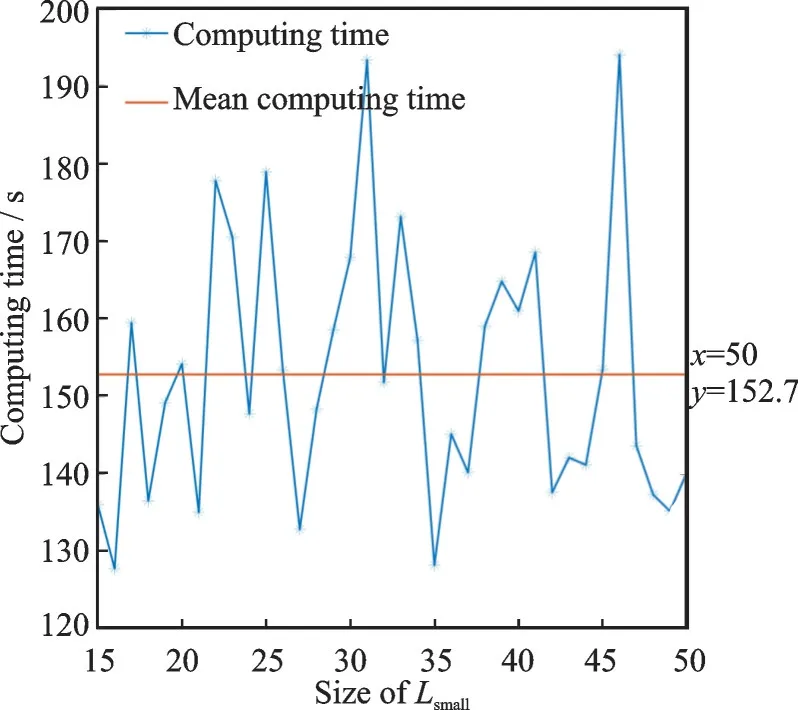
Fig.17 Relationship between the size of Lsmall and the computing time by space splitting optimal method
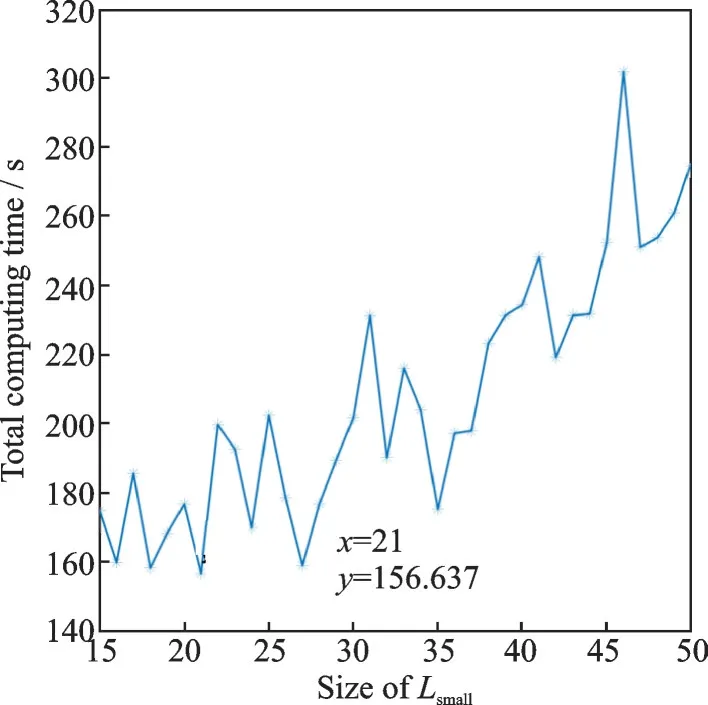
Fig.18 Relationship between the size of Lsmall and the total computing time
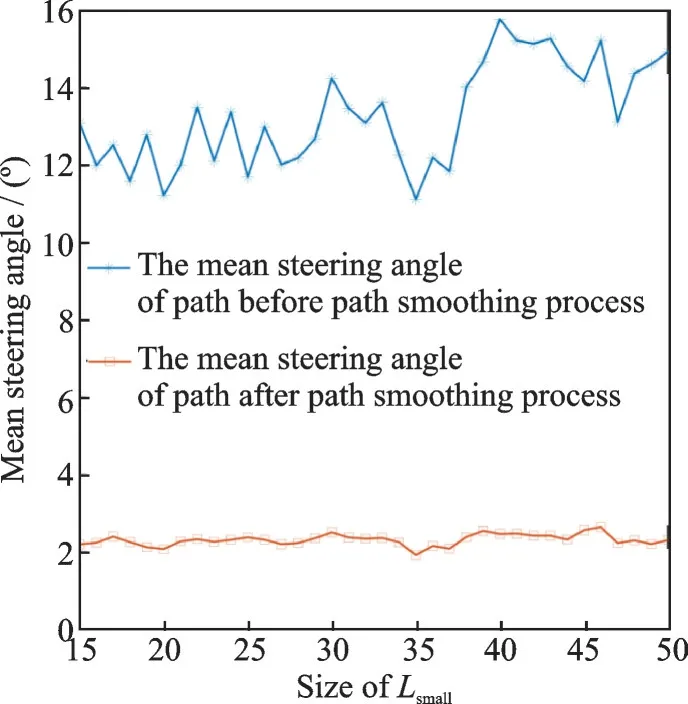
Fig.20 Relationship between the size of Lsmall and the mean steering angle
The computing time by the space splitting optimal method fluctuates constantly, but there is no pronounced changing trend.
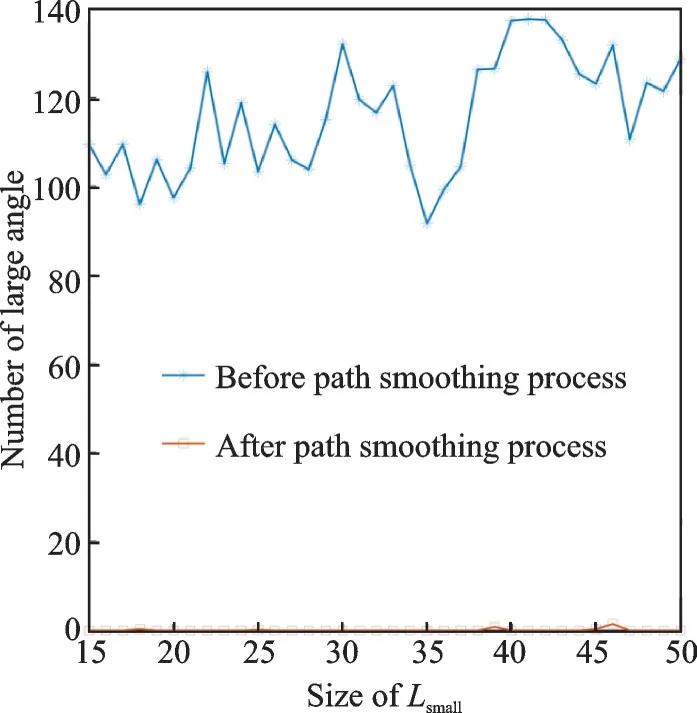
Fig.21 Relationship between the size of Lsmall and the number of large angle
By comprehensively considering the size ofLsmalland time-consuming, when the size ofLsmallis in the range of 15—27, the algorithm has less timeconsuming.
The relationship between the size ofLsmalland the path length is shown in Fig.19.
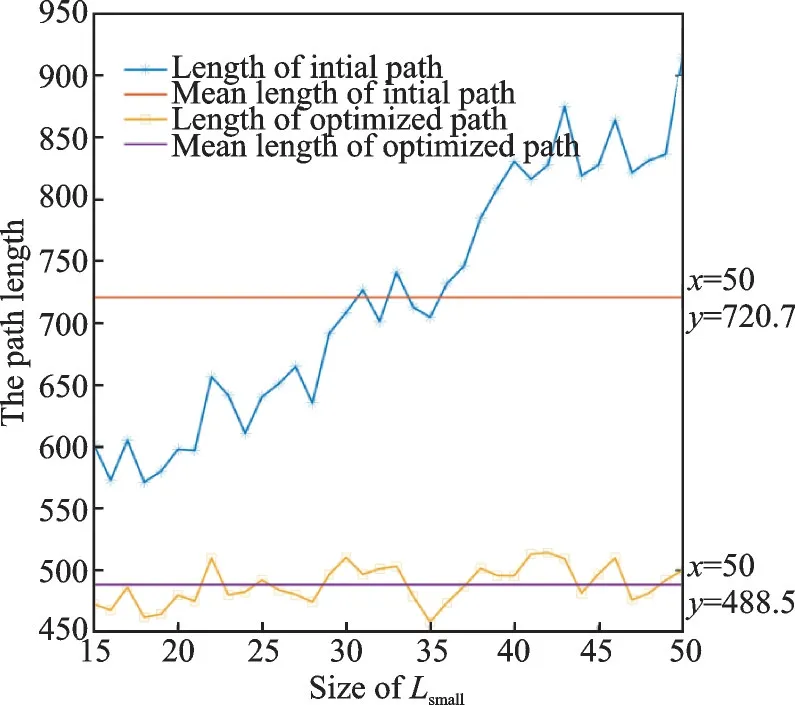
Fig.19 Relationship between the size of Lsmall and the path length
The length of the initial path generated by the path mapping method has a growth trend as the size ofLsmallincreases. However, the length of the optimized path always fluctuates within a small range, proving that the space splitting method can optimize the path effectively.
The relationship curve between the size ofLsmall, the mean steering angle and the number of large angles are as below.
From the simulation results, it can be concluded that the smoothness method proposed by Refs.[12-14] can be used for path planning smoothing effectively.
There remain many methods of path planning. In this scenario, the comparison curves and analysis among the multi-scale method and A* algorithm has been done to verify the efficiency of the presented method,as shown in Figs.22,23,respectively.
The size ofLis 300×300, the start position inLis at the 300th row and the 1st column, and the target is at the 2nd row and the 300th column.
In the multi-scale method, TCmax=0.4 and the path planning parameters inLNeware:N=40,M=50,τmin=0.1. The path planning parameters inLpassare:N=30,M=40,τmin=0.1, and the size ofLsmallis 15×15. Regional optimization parameter are:Onum=150,Pmax=0.085,Pmin=0.05,Nsmall0=40, andMsmall0=50.
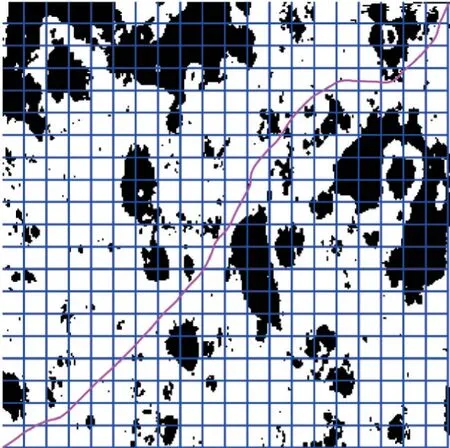
Fig.22 Final optimal path by multi-scale method

Fig.23 Final optimal path by A* algorithm
The optimal path generated by the multi-scale method is 463.92 long, which costs 79.643 s; the optimal path generated by the A* algorithm is 458.17 long, which consumes 295.987 s. Hence, the multi-scale method has significantly improved the searching speed.
The proposed method can search optimal path in global space with different start positionSand target positionT. Fig.24 presentsSat the 150th row and the 1st column, andTat the 630th row and the 660th column.
4 Conclusions
This paper proposes a multi-scale method based on ant colony algorithm. The certain idea are path mapping and space splitting method. Several simulations are presented to demonstrate the effectiveness of the theoretical result. The multi-scale improved ant colony algorithm can improve the search speed and find the global optimal solution effectively. Multi-scale ant colony algorithm is beneficial to plan the path of the lunar robots efficiently and stably. It can be extended to large-scale path planning problems with complex terrain requirements in various fields in the future.
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Analysis of Magnetic Positioning for Liquid Oxygen Under Microgravity Condition
- Mechanical Analysis and Numerical Simulation for New Type of Dynamic Control Devices
- Structural Dynamic Optimization for Flexible Beam of Helicopter Rotor Based on GA
- Aircraft Optimal Separation Allocation Based on Global Optimization Algorithm
- Adaptive Tracking Control for Diffractive Film Based on Nonlinear Sliding Mode
- Iterative Identification of Robot Dynamic Parameters Based on Logistic Function
