基于PSO-X算法的交通信号区域协调控制模型 *
2022-02-10徐建闽首艳芳
徐建闽,周 传,首艳芳
(1. 华南理工大学 土木与交通学院, 广东 广州 510640;2. 华南理工大学 广州现代产业技术研究院, 广东 广州 510640)
0 引 言
随着汽车保有量增加,道路堵塞已经成为城市发展的一大瓶颈。因此,为解决城市道路堵塞问题,一方面需要拓宽道路提高道路通行能力,另一方面需要采取有效的交通控制方法。城市交通信号控制按照控制范围不同可分为单点信号控制、干线协调控制和针对交通区域的区域协调控制。对于现在复杂多变的交通环境,仅仅单交叉口信号控制和干道协调控制已经不能满足城市交通的需求,许多学者已经对交通区控制方法进行了大量研究。K. ABOUDOLAS等[1]建立了以平衡链接队列最小为目标的二次规划控制模型,提出了一种新信号控制方法,该方法为大规模城市交通网络中的全网络实时信号控制提供了一种计算上可行的技术,同时也适用于拥挤的交通条件,随着信号控制区域增大、信号交叉口数量增加控制模型的求解变得越来越难;别一鸣等[2]综合考虑不同相位差和闭环相位差对于每周期车辆的阻滞作用,建立了以协调控制损失效益最小化的相位差优化的模型;支俊等[3]分别在高峰期、平峰期和低峰期的城市交通状态下对区域协调控制中不同的相位差方案进行研究。
综上所述,以上研究模型指标过少或难以对路网区域进行有效协调控制,在城市交通区域出现拥挤时不利于车流快速疏导。针对上述情况,笔者建立了以区域输出车流量、交叉口路段排队长度和总延误3个性能指标为目标,以路段排队车辆数、最大和最小周期、闭合相位差与绿灯时间之间约束关系作为约束条件的交通区域交叉口协调控制模型。
1 城市交通区域路网模型
对一个路网进行信号控制的一般步骤为:先对相邻交叉口进行关联度分析划分子区域,再对各子区域内信号交叉口进行信号配时[4]。笔者研究重点为已经划分好的子区域,再对区域内交叉口进行关联度分析,对区域内信号交叉口进行合理配时,提高整体路网的通行效率。
城市交通区域路网的描述如下:设城市交通区域路网内交叉口总数量为N,所有交叉口均为信号交叉口;设I为区域路网内交叉口集合,对于任意交叉口i,有i∈I;设P为信号配时方案集合,Pi为交叉口i的信号配时方案;Fi为交叉口i相位数;交叉口i的进口道数为Ji,其中进口道j车道数为Jij。假设每个信号交叉口都有东西南北4个方向的进口道,每个进口道都是双向六车道,即将对于任意交叉口i有Ji=4、Jik=3。
2 城市交通信号区域控制模型
2.1 公共周期
要进行区域协调控制首先要确定公共周期[5],公共周期决定区域内交叉口交通状态,作用是使区域内交通状态最差的交叉口不产生过饱和,协调信号配时,提高区域通行能力[6]。式(1)为初始公共周期取值范围。
(1)
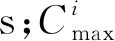
[Cmin,Cmax]为公共周期的取值范围[7]。
2.2 区域交通信号控制模型
区域交通信号控制模型多以延误和排队长度作为优化目标,但随着城市的发展交通情况的复杂多变,某些路段因为上游交叉口车辆到达数量过多而产生“无绿灯的”现象,造成路网发生交通拥堵,降低了该区域通行能力[8]。所以仅以延误和排队长度作为模型的优化目标已经不能满足区域协调控制的目的。基于此,提出了以区域总输出流量最大和交叉口排队长度、延误最小的区域交通信号控制模型[9]。函数Ob如式(2):
(2)
式中:
(3)
(4)
(5)
其中:
(6)
(7)
(8)
(9)
(10)
(11)
Cmin≤Ck≤Cmax
(12)
(13)
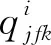
2.3 相邻交叉口相位差
相位差决定上游车辆到达下游时刻,影响车辆在道路中行驶状况[11]。在低饱和交通状态下,信号周期内排队车辆能在绿灯时间内全部驶离,不会产生排队累计影响下一周期车辆;而在近饱和与高饱和的交通状态下,往往会出现二次排队现象,车队尾部的车辆因为排队在绿灯时间内无法驶离,需要等待下一次绿灯[12]。因此,理想相位差应保证在上游交叉口绿灯亮后,车辆从上游行驶到下游车队尾部正好为下游消散波传到车队尾部的时刻[13]。所以理想的相位差应该满足式(14):
(14)
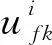
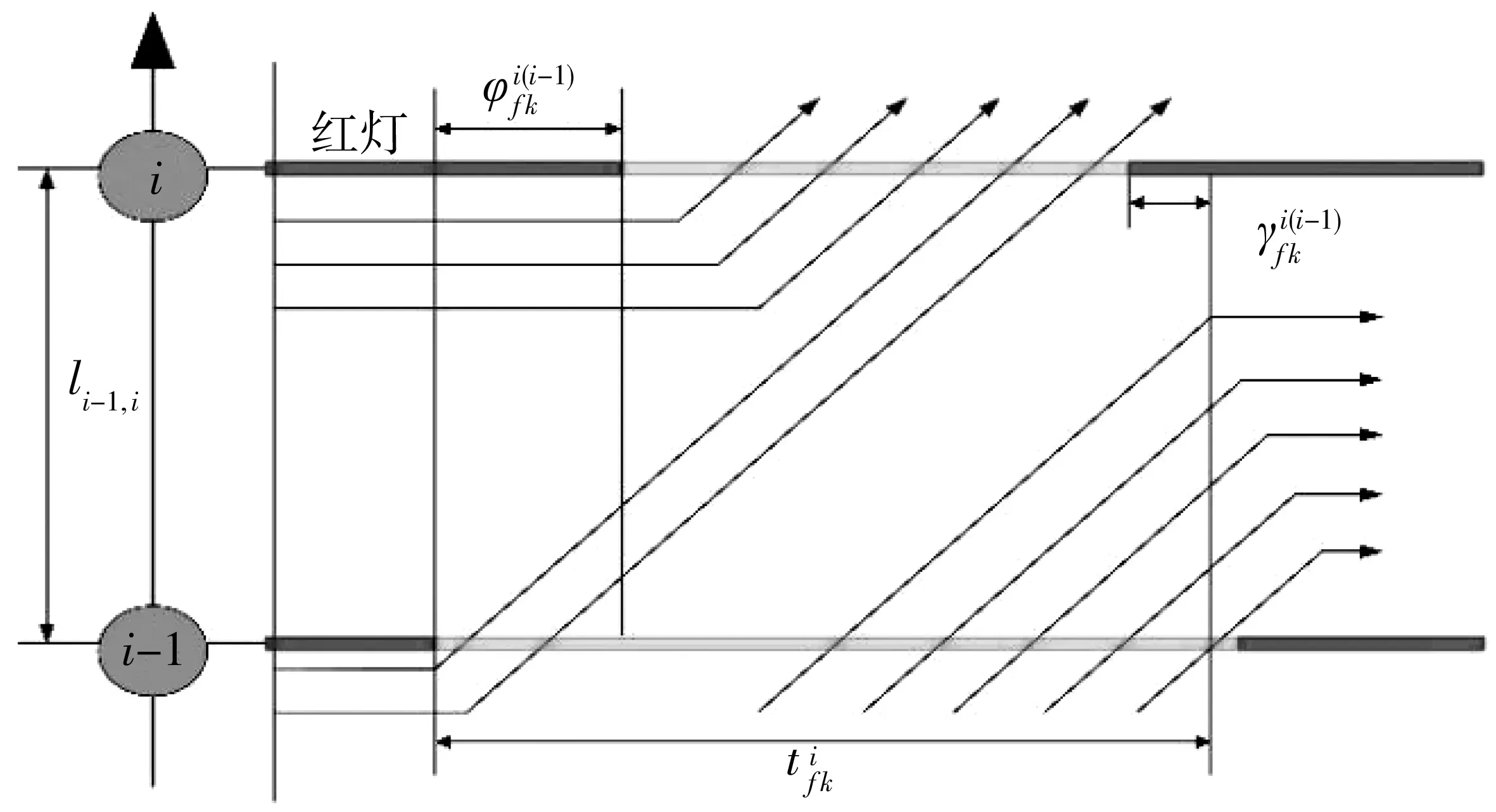
图1 交叉口时距Fig. 1 Time distance of intersection
2.4 模型的求解
由于笔者建立的信号控制模型具有目标多、变量多和变量维度高、约束条件多且复杂的特点,其解向量的空间范围广,经典粒子群算法调节参数固定,缺乏对粒子速度调节,容易导致算法收敛精度低或者不易收敛。例如:加速常数c1和c2、惯性权重ω。加速常数c1和c2决定粒子自身运动轨和其他粒子运动对粒子运行速度影响,体现了粒子之间的交流;c2设置过大,又会导致算法过早收敛精度低。为了达到全局搜索与局部搜索两者间的有效平衡,需要对粒子的速度进行有效控制,故采用改进粒子群算法,增加收缩因子。公式为:
Vmd(t+1)=μ[Vmd(t+1)+c1ξ(pmdt-Xmdt)+c2η(ptg-Xmdt)]
(15)
Xmd(t+1)=Xmdt+Vmd(t+1)
(16)
(17)
式中:Vmdt为粒子m第t次迭代d维度的速度;Xmdt为粒子m第t次迭代d维度的位置;μ为惯性权重;ξ和η为0~1之间的随机数;pmdt和ptg分别为第m粒子第d维度的个体极值点和全局极值点。
先确定初始公共周期,观察区域内相邻交叉口的特点,根据式(14)和模型中的约束条件确定交叉口之间的相位差;再通过算法(PSO-X)计算得区域内交叉口优化绿灯时间和公共周期。其具体步骤为:
Step1开始,输入该交通区域内各交叉口参数。
Step2采用式(1)计算区域内交叉口周期,根据式(1)确定公共周期范围[Cmin,Cmax];再根据区域内相邻交叉口的特点,利用式(13)和约束条件计算出相邻交叉口的相位差。
Step3初始化算法粒子数Np、速度最大值Vmax和速度最小值Vmin、加速常数c1和c2、惯性权重ω、最大迭代次数Tmax,另Ck=Cmin,t=1。
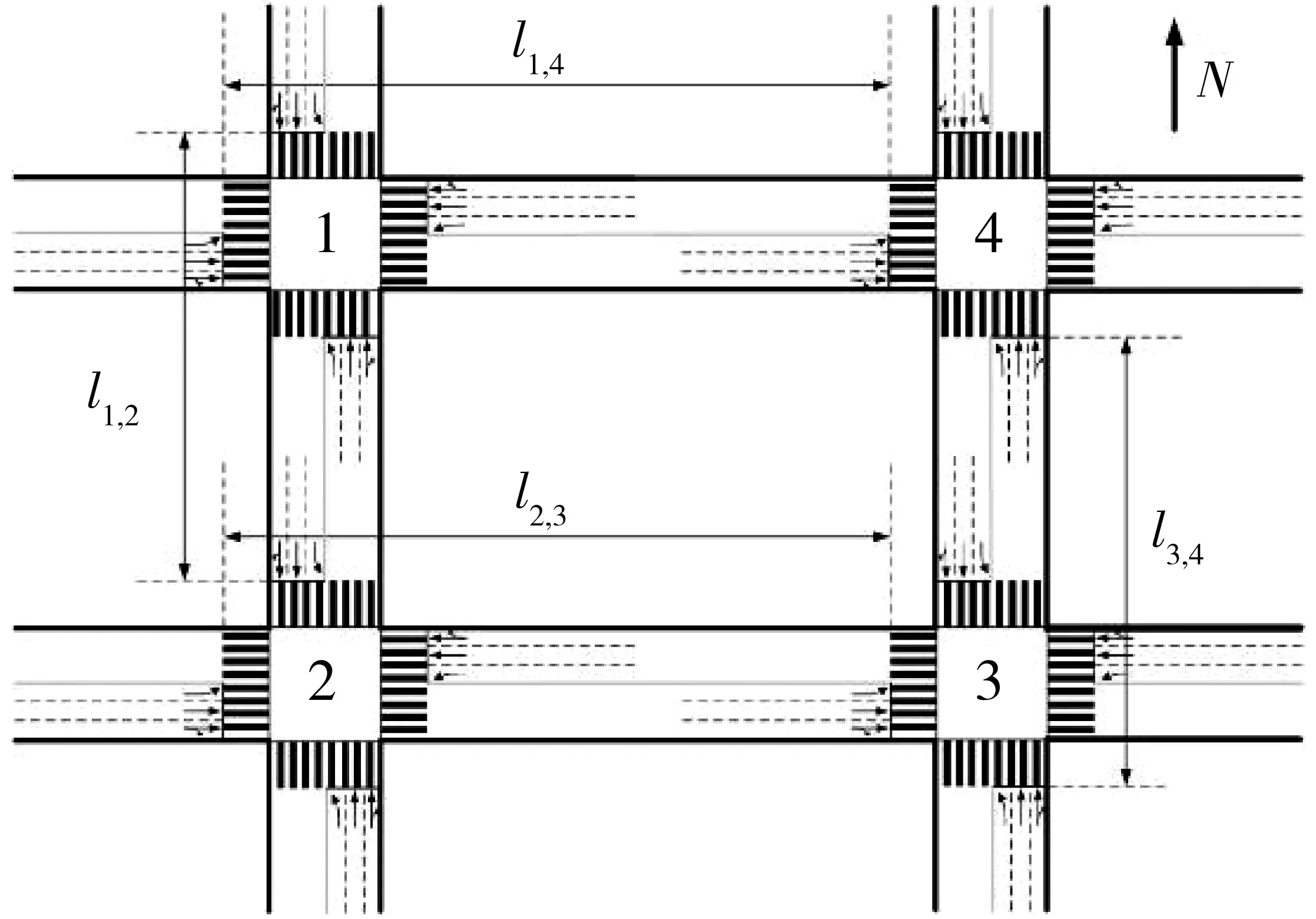
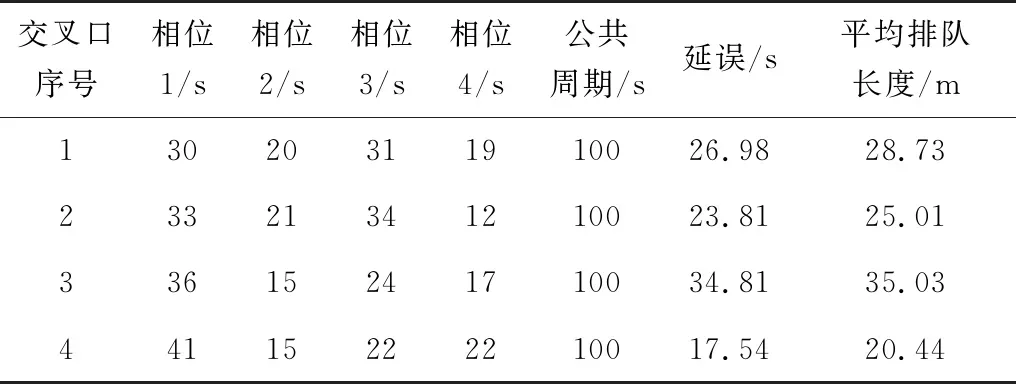
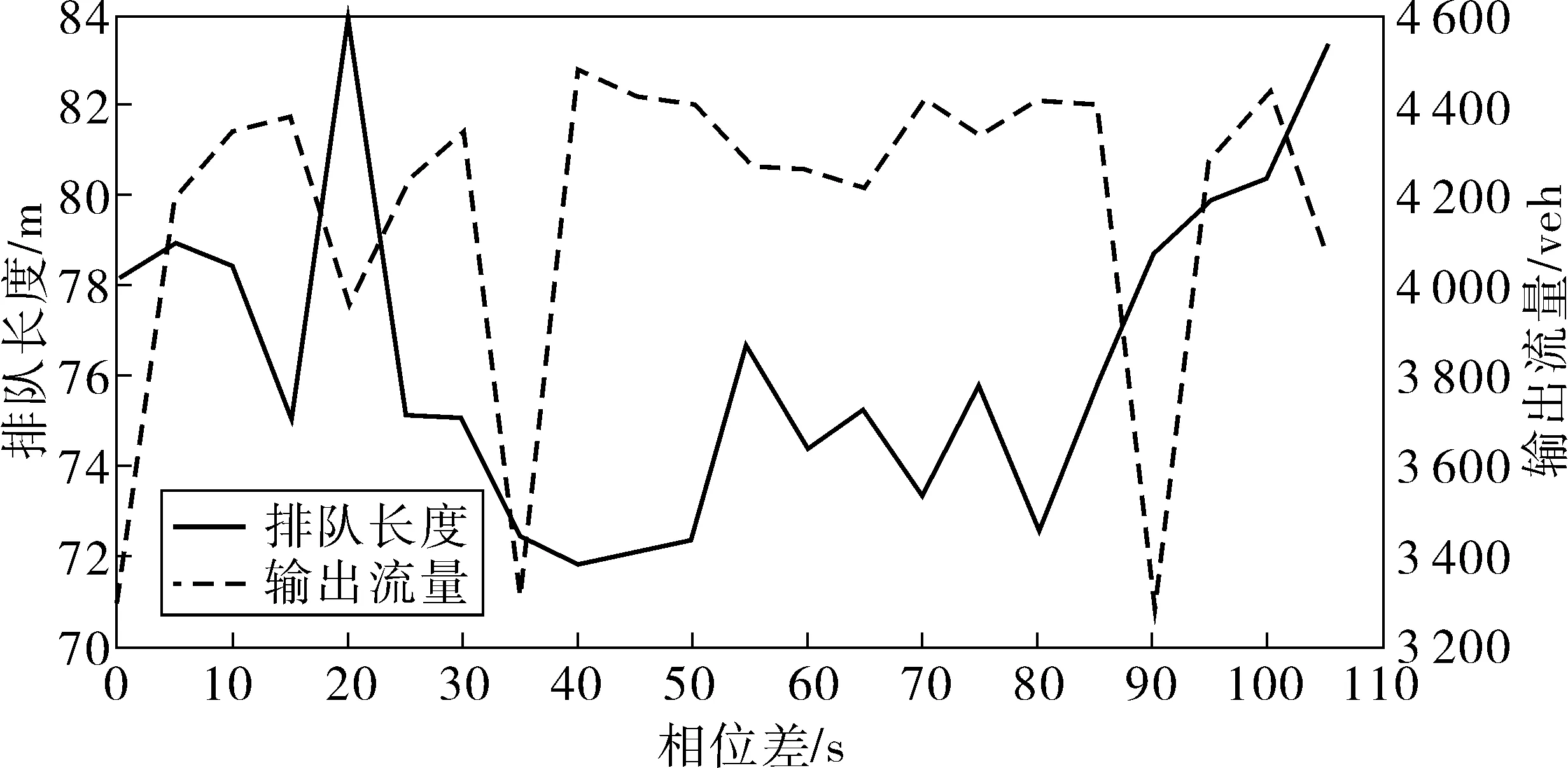
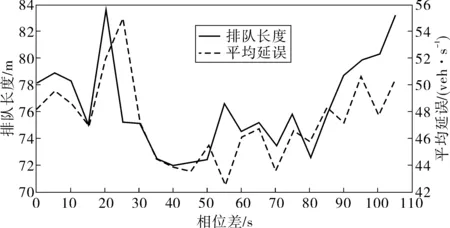
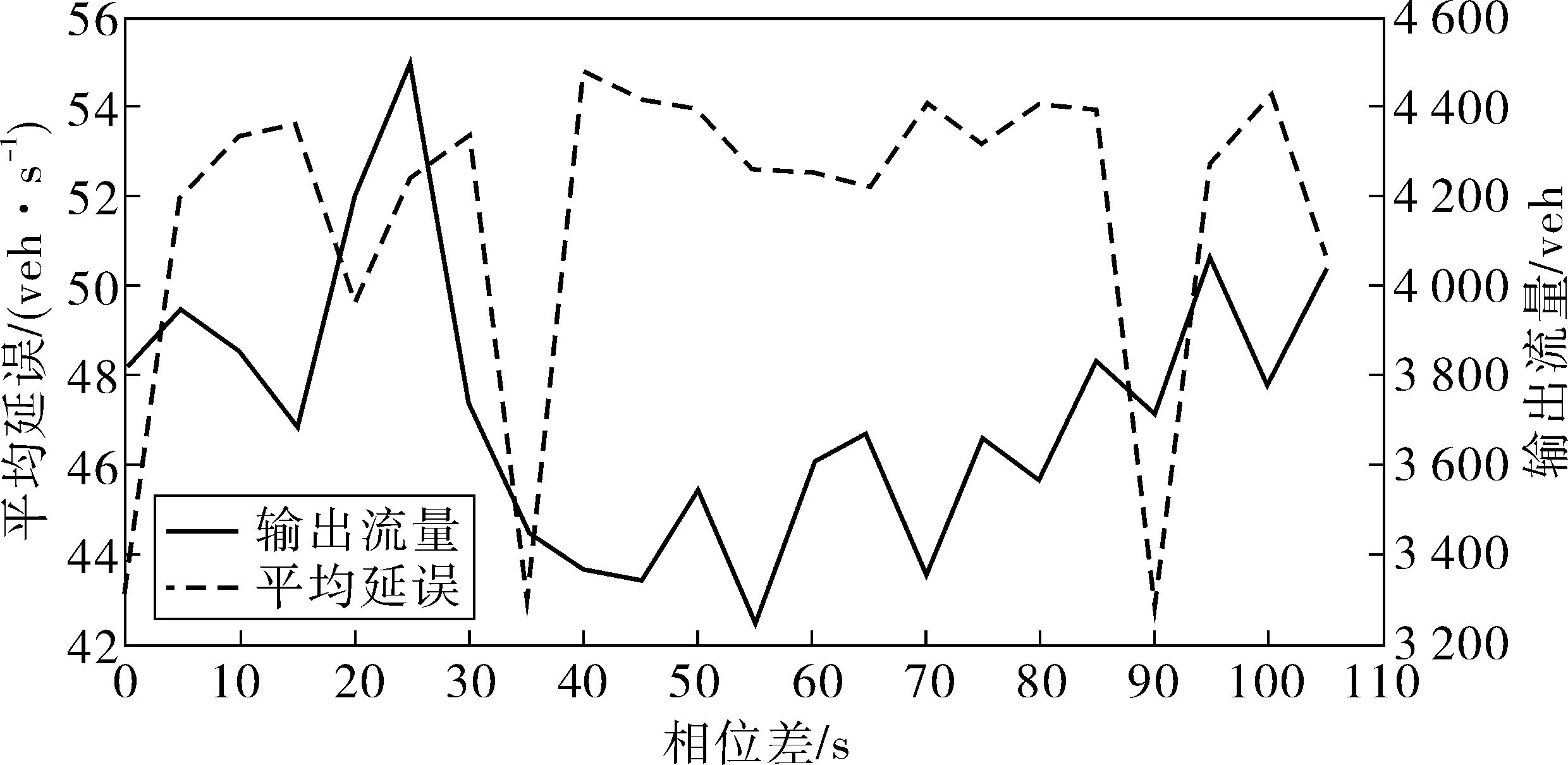
Step4判断公共周期Ck是否满足Ck Step5判断迭代次数t是否满足t Step6更新适应度值,利用式(15)~式(17)更新粒子速度和位置;t=t+1,Ck=Ck+1;转到Step4。 Step7找到适应度函数最小值时的解Ck、有效率绿灯等。 Step8结束,输出最优解。 算法流程如图2。 图2 算法流程Fig. 2 Algorithm flowchart 为验证模型有效性,选取由某4个交叉口组成交通区域路网作为控制对象,该路网包括12条进口道(图3)。在MATLAB上实现算法编程,使用Vissim软件实现对路网仿真,将仿真结果与Webster延迟模型进行比较。区域内各进口道饱和流量为1 800 veh/h,行驶速度为40 km/h,其中交叉口1与交叉口2之间距离l1,2为300 m,交叉口2和交叉口3距离l2,3为450 m,交叉口3与交叉口4距离l3,4为300 m,交叉口1与交叉口4距离l1,4为450 m,Cmax为120 s,Cmin为80 s,各交叉口有效绿灯时间区间为10~45 s,路网区域内交通流量如表1,交叉口采用相位如图4。 图3 路网结构Fig. 3 Road network structure 图4 交叉口相位相序Fig. 4 Phase sequence of intersection 表2为Webster模型相位配时方案及仿真结果,表3为文中模型相位配时方案及仿真结果,表4为Webster模型和文中模型输出车流量仿真结果对比。 表1 路网交通流量Table 1 Road network traffic flow veh/h 表2 韦伯斯特优化配时结果Table 2 Webster optimization timing results 在低饱和状态下,主要关注的是交叉口的延误和排队,一定的时间内区域输出的流量差别不大。调整权重W1和W2使延误和排队比例更高,在优化时优先考虑延误和排队。根据文中模型,实验结果显示:交叉口1延误减少15.0%,排队长度减少0.4%;交叉口2延误减少3.8%,排队长度减少2.59%;交叉口3延误减少23.38%,排队长度减少26.57%;交叉口4延误减少6.10%,排队长度仅减少6.75%。可以看出在低饱和状态下,该模型相比延迟模型有更低延误和排队长度。 当城市交通区域内交叉口处于高饱和状态下,为防止排队溢出和增大输出流量,调整权重W1和W2,使平均排队长度和区域向外输出流量在目标函数中的比例变高,同时根据式(13)调整相邻交叉口之间的相位差,协调上下游交叉口信号控制。实验结果如表3、表4。 表3 文中模型优化配时方案Table 3 Optimization timing scheme of the proposel model 表4 VISSIM仿真结果输出Table 4 Output of VISSIM simulation results Webster模型以延误最小为指标,而在高饱和状态下,由于短时间车流量较大容易产生排队溢出,进而影响上游的交叉口运营情况,所以对于高饱和状态下仅仅选取延误作为控制指标是不合适,排队长度和区域出流量同样需要作为优化目标指标考虑。仿真结果显示笔者提出的模型总输出的车辆数提高了8.25%,平均排队长度减少了5.54%。 高饱和条件下,交叉口1和交叉口4之间的排队长度、延误和输出流量随相对相位差的变化情况如图5~图7。图6显示排队长度和平均延误随相对相位差的变化趋势大致相同,在相对相位差为40 s左右时取得最小值;对于输出流量这一指标,同样也在相对相位差为40 s时获取最大值,所以交叉口1~交叉口4之间的最优相对相位差取为40 s。 图5 交叉口1~交叉口4性能指标随相位差变化(排队长度和输出流量)Fig. 5 Variation of performance indicators at intersections 1~4changing with phase difference (queue length and output flow) 图6 交叉口1~交叉口4性能指标随相位差变化(平均延误和排队长度)Fig. 6 Variation of performance indicators at intersections 1~4changing with phase difference (average delay and queue length) 图7 交叉口1~交叉口4性能指标随相位差变化(平均延误和输出流量)Fig. 7 Variation of performance indicators at intersections 1~4changing with phase difference (average delay and output flow) 提出了以交通区域内的总延误和排队长度最小、向外输出交通流量最大为控制指标的区域协调控制模型。结果显示:低饱和状态下,提出模型相比延迟模型有更低延误和排队长度;在高饱和状态下,相比与Webster模型以延误为控制指标,笔者模型提出以排队长度最小指标能减轻在高交通流量下排队长度溢出对于上下游交叉口的影响,同时以减轻高峰时期区域内拥堵为目标,增加高峰时期区域内向外输出交通流量最大作为控制指标。仿真结果显示能有效降低排队和延误、增加区域高峰时期向外输出的交通量。 虽然笔者提出的区域协调控制模型在减少区域内交叉口延误、排队长度和增加高峰时期区域向外输出交通流量有一定效果,但由于城市交通状况复杂多变,对各交叉口进口道流量不均而导致各交叉口周期差异大和采用不同相位相序的情况将成为下一步研究的方向;同时,随着区域内交叉口数量增多,通过算法求解出的解向量维度越大,最优解越难获取,需要选取更合适的算法进行求解。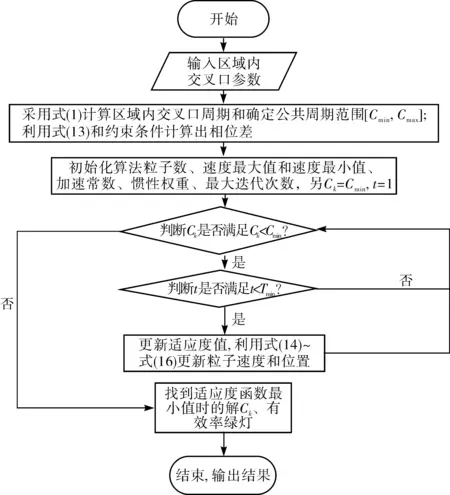
3 算例分析


4 结 语
