基于响应曲面法风电齿轮箱行星架拓扑优化设计 *

雷 林，丁明泽，胡洪伟，张 敏，侯怡鑫

(1. 重庆交通大学 航运与船舶工程学院，重庆 400074； 2. 中船重工(重庆)西南装备研究院有限公司，重庆 401147)

0 引 言

风能作为一种清洁能源发展的新趋势，逐渐受到学者的关注。风电齿轮箱是风力发电领域的重要设备，均采用行星传动，是典型的低速、重载、变转矩和增速传动。

在齿轮箱的故障率中，行星传动相关的故障率约占40%[1]。行星架结构设计及性能参数直接影响风电齿轮箱的传动效率和效果。行星传动简图如图1(a)[2]，行星架三维模型如图1(b)。

图1 行星架工作原理及结构Fig. 1 Working principle and structure of planet carrier

此外S.SANKAR等[11]、YI Pengxing等[12,15]、D. M. BLUNT等[13]、HAO Dongsheng等[14]分别就风力发电机齿轮箱轴承失效形式、多目标性能提高、检测其疲劳裂纹方法、行星齿轮架和轴组件的过盈配合和模态特性等方面展开相应研究。

上述学者针对风电齿轮箱行星架进行拓扑优化的过程当中，均以某一个或某几个指标作为优化目标，并未考虑风电齿轮箱行星架的综合结构性能展开分析与优化。因此笔者结合呼斯乐图等[9]、杨龙[10]对其他不同应用领域的行星架研究成果，以结构轻量化及提高结构性能为目标进行综合考量，对某型号风电齿轮箱行星架展开拓扑优化设计。

根据GB/T 19073—2018《风电发电机组齿轮箱设计要求》，应依据第四强度理论(Von Mises应力)评估行星架静态承载性能。根据有限元分析结果，采用基于响应曲面法的拓扑优化遗传算法，以行星架自重、形变量及Von Mises应力值作为优化目标，针对行星架进行尺寸优化设计，最终获得该型号行星架结构最佳方案。

1 行星架有限元前处理

1.1 行星架材料参数

笔者所分析的风电齿轮箱行星架材料参数如表1。

表1 行星架材料参数Table 1 Material parameters of planetary carrier

1.2 行星架模型简化

对行星架几何模型进行适当简化，将花键部位进行光滑处理，在保证对结构强度和变形形变影响较小的前提下，避免细微结构引起的网格畸形，简化后行星架三维模型如图2。

图2 行星架简化三维模型Fig. 2 Simplified three-dimensional model of planetary carrier

1.3 边界条件及载荷施加

对单独风电齿轮箱行星架进行有限元分析时，在4个行星轮轴孔处施加反向转矩。反向转矩总和等于输入转矩，载荷类型为面载荷[2]，转矩为 46 240 N·m。加载方式如图3中B、C、D和E。

2.2.4 混播比例对混播植物Pro含量的影响 不同混播比例对禾草Pro含量均无显著影响(表3)，而对苜蓿Pro含量有明显影响(表4)。B1处理Pro含量最高，比B2，B3和B4处理高24.48%，27.41%和49.50%，差异极显著(P<0.01)；单播苜蓿苜蓿Pro含量分别比B3和B4处理高17.77%(P<0.05)和38.19%(P<0.01)，B2处理Pro含量比B4处理高20.10%(P<0.05)，其余处理间苜蓿Pro含量无显著差异(P>0.05)。

行星架端面施加完全固定约束，如图3中A；考虑圆柱滚子轴承支承作用，在左右两侧圆柱面上施加径向约束，如图3中F和G[8]。

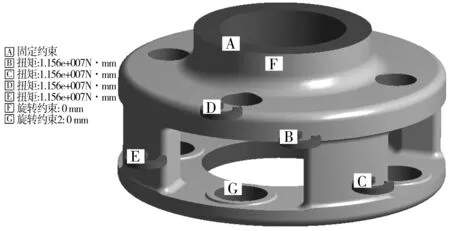
图3 边界条件及载荷施加Fig. 3 Boundary conditions and load application diagram

1.4 网格无关性验证

对风电齿轮箱行星架进行有限元网格划分，全局使用六面体网格，尺寸设置为6 mm。为研究网格特性，局部使用不同尺寸的面网格进行加密，具体加密区域如图4，最大Von Mises应力值变化趋势如图5。

图4 局部网格加密区域Fig. 4 Local grid encryption area

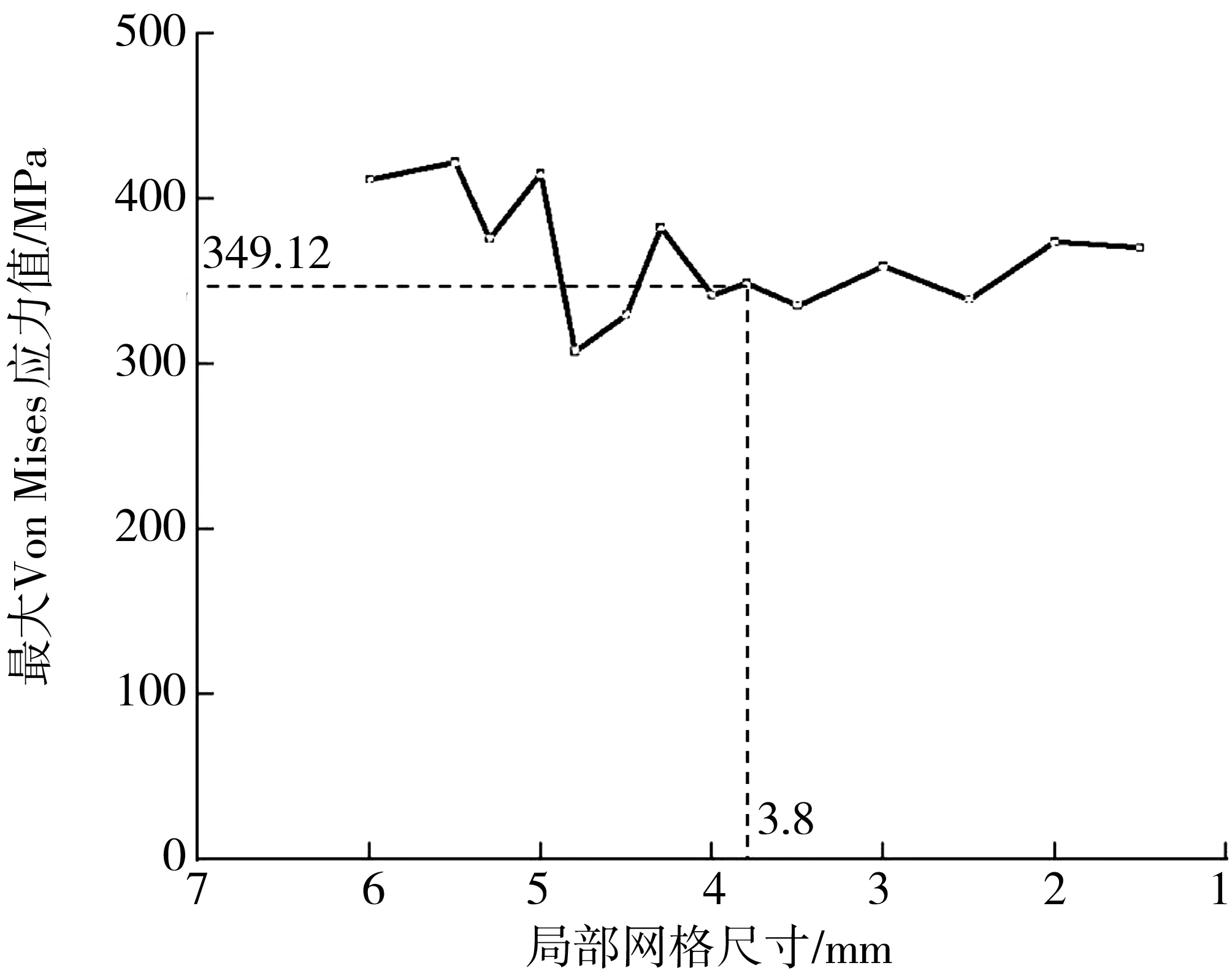
图5 最大Von Mises应力走势Fig. 5 Trend chart of maximum Von Mises stress

综合权衡计算精度和成本，选择应力变化幅度5% 作为网格无关性判据，以全局网格尺寸6 mm、局部网格尺寸3.8 mm作为最终网格划分方案，总计55 236 个节点，71 788个单元。

2 行星架拓扑优化设计

2.1 优化设计数学模型

优化设计主要包括设计变量、目标函数以及约束条件。设计变量是优化设计中待确定的参数。目标函数是优化设计中用于判别设计方案优劣标准的数学表达式，常用F(X)表示,如式(1)：

(1)

式中:μ为权重系数;xi为设计变量。其中，设计变量的个数确定了目标函数的维数，设计变量的幂及函数值确定了目标函数的性质。优化设计中寻求目标函数极值的某些限制条件，称为约束条件。最优化问题的基本表达式通常如式(2)～式(5)[16]：

X={x1,x2,x3,…,xn}T(X≥0)

(2)

F(X)→min(或max) (X≥0)

(3)

hj(X)=0 (j=1,2,…,k；X≥0)

(4)

Gi(X)≤0 (i=1,2,…,n；X≥0)

(5)

式中:X为设计变量的集合；F(X)为目标函数；hj(X)、Gi(X)以及X≥0分别表示优化问题中该满足的约束条件。

2.2 拓扑优化

2.2.1 响应曲面及灵敏度分析

利用响应曲面方法对风电齿轮箱行星架进行分析，首先要提取数个预估变量参数。根据张立勇[4]、东立剑[5]的研究，笔者初步选取输入端面拉伸量x1、输入端面环半径x2、输入端面四销轴孔半径x3和轴肩倒角半径x4为预估变量参数，其中输入端面拉伸量即决定输入端面厚度D1(图6)，同时确定预估变量参数及设置变量参数范围，各变量参数初始值及所取变量参数范围如表2。

表2 预估变量参数值Table 2 Estimated variable parameter value

图6 预估变量参数Fig. 6 Estimated variable parameters

笔者以降低风电齿轮箱行星架自重、最大Von Mises应力值及最大形变量作为优化目标，基于Workbench平台，利用响应曲面法进行计算求解，可以得到25组符合范围要求的不同变量参数数值及其所对应的优化目标值，即行星架自重、最大Von Mises应力值和最大形变量值，其中：F1(X)为行星架自重；F2(X)为行星架最大Von Mises应力值；F3(X)为行星架最大形变量。

由数据统计结果可得各优化目标响应曲面，如图7。行星架自重响应曲面代表预估变量x1、x2、x3和x4与行星架自重之间的关系。分析图7(a)可知，随x1和x4增加，行星架自重增大；随x2和x3增加，行星架自重减小。

行星架最大Von Mises应力值响应曲面代表预估变量与行星架最大Von Mises应力值之间的关系。分析图7(b)可知，随x1、x4增加，最大Von Mises应力值减小；随x2、x3增加，最大Von Mises应力值增加。

行星架最大形变量响应曲面代表预估变量与行星架最大形变量之间的关系。分析图7(c)可知，随x3增加，最大形变量增大；随x1、x4增加，最大形变量减小；x3对最大形变量影响较小。

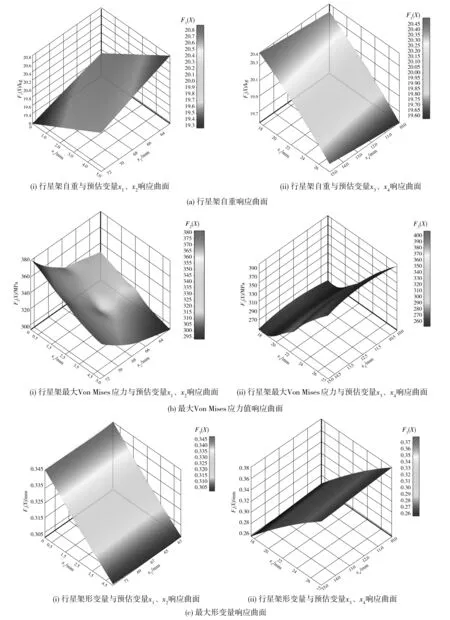
图7 各优化目标响应曲面Fig. 7 Response surface of each optimization target

对综合响应面模型进行分析可知，所选参数之间的组合对行星架的自重、最大形变量和最大Von Mises应力起着重要的作用。单一因素的改变不能从整体上改变行星架的性能，需要对输入参数进行有效组合，才能合理优化行星架的性能[5]。

灵敏度分析是对模型参数的动态变化过程(即瞬时变化过程)进行分析，研究特定参数对模型性能的影响情况[8]。针对笔者所研究的风电齿轮箱行星架，对于自重、最大Von Mises应力值和最大形变量，各预估变量参数的灵敏度如图8。

图8 各变量灵敏度Fig. 8 Sensitivity relationship of each variable

根据所得响应曲面及灵敏度结果，各变量参数与优化目标之间的关系如表3。

表3 各变量参数与优化目标之间的关系Table 3 Relationship between various variable parameters andoptimization objectives

2.2.2 尺寸优化设计

通过各预估变量响应曲面分析及灵敏度分析，可以进行优化变量提取，最终确定x1、x2、x3为优化方案变量，修正优化方案变量参数范围，如表4。

表4 优化方案变量参数值Table 4 Variable parameter value of optimization scheme mm

根据优化变量参数及参数范围展开尺寸优化设计。综合考虑计算资源及样本可靠性，提取100组优化设计方案，成功优化方案99组，并基于优化目标(行星架自重、最大Von Mises应力值和最大形变量)进行排列组合，选取最优解，最终获得3组最佳优化方案，如表5。

2.3 结构优化前后性能分析

综合考虑优化设计方案，以风电齿轮箱行星架结构轻量化作为衡量标准，选取表5中优化方案2作为优化设计方案。行星架结构优化前Von Mises应力分布及形变分布如图9；行星架结构优化后Von Mises应力分布及形变分布如图10。

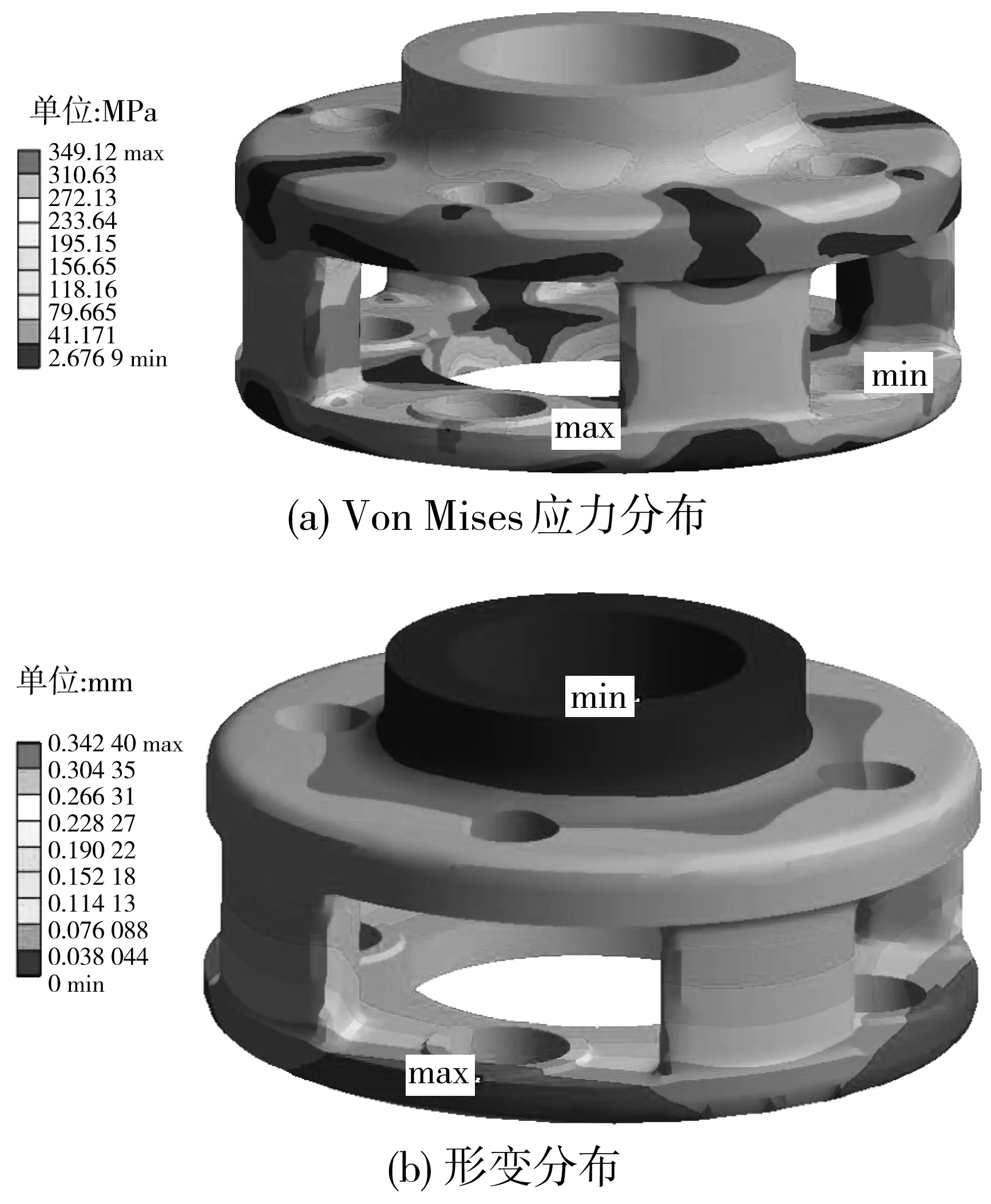
图9 优化前行星架Von Mises应力及形变分布Fig. 9 Distribution of Von Mises stress and deformation of theplanet carrier before the optimization

图10 优化后行星架Von Mises应力及形变分布Fig. 10 Distribution of Von Mises stress and deformation of theoptimized planet carrier

优化方案2下，优化前后数据对比如表6。

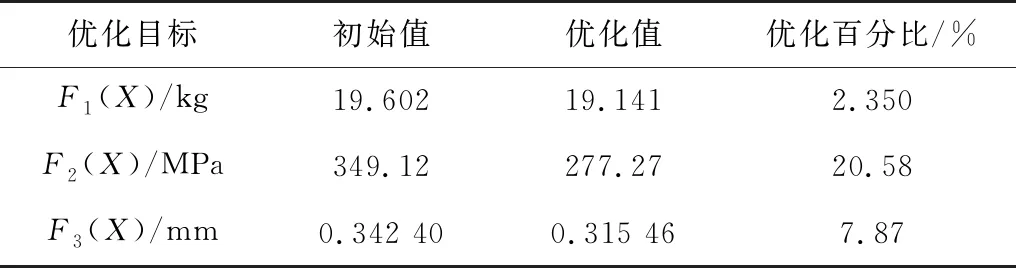
表6 优化前后数据对比Table 6 Data comparison before and after optimization

3 结 语

笔者建立某型号风电齿轮箱行星架三维模型，开展有限元分析，基于响应曲面法，以结构轻量化、减小最大Von Mises应力值及降低最大形变量作为优化目标，将行星架输入端面拉伸量x1、输入端面环半径x2和输入端面四销轴孔半径x3作为优化过程中的关键影响因素，并分析设计变量与优化目标之间的关系，从而进行拓扑优化。

根据99种优化方案，最终基于优化目标进行综合考虑，选取该型号风电齿轮箱行星架结构的最佳优化方案。结果表明，行星架自重降低2.35%，最大Von Mises应力值降低20.58%，形变量降低7.87%，充分提高了该型号行星架综合性能。为了更好地提高性能参数，可进行疲劳分析及实验，展开进一步优化。