基于优先权的铁路多事故点应急资源调度多目标优化研究

2022-02-10汤兆平余时钧宫素萍孙剑萍

重庆交通大学学报(自然科学版) 2022年1期

汤兆平,余时钧,宫素萍,孙剑萍

(1. 华东交通大学交通运输与物流学院，江西南昌 330013; 2. 合肥市轨道交通集团有限公司，安徽合肥 230000)

0 引言

近年来，随着我国铁路路网建设规模的扩大、列车速度的提升以及各种自然灾害的影响，同一区域路网内同时多处发生突发事故的风险正在加剧，从而可能引发多个事故点对应急资源需求的竞争与冲突问题。因此，需要研究多事故点的应急资源调度优化问题。

国内外学者针对多事故点的应急资源调度研究已经取得了一定成果。杜雪灵等[1]考虑到多个事故点之间的公平性，以救援公平性最大和调度总成本最小为优化目标，构建多目标多事故点应急资源调度模型；杨继君等[2]结合博弈论理论，针对应急资源物资分配公平性问题，将调度过程划分成多个阶段，建立了面向多事故点需求的博弈调度模型；陈刚等[3]在多事故点的应急资源分配问题中，在追求效率的同时通过量化嫉妒心理来表现公平，构建以比例公平为约束条件的应急物资分配优化模型；陈治亚等[4]考虑在资源短缺情况下，采用遗传退火混合算法对多受灾点、多资源、多出救点的资源调度优化模型进行求解；D.RUBEL等[5]针对多灾点应急资源配置效率低下的问题，建立了基于Agent的多灾点应急资源配置模型;ZHOU Yawen等[6]在多事故点的的情形下，建立了多时段动态应急资源调度的多目标优化数学模型；王妍妍等[7]在指数效用函数中引入灾民物资需求的比例短缺测度公平，以物资短缺的延迟损失最小化与物资分配的总成本最小化为目标，构建了多受灾点应急物资动态多阶段分配模型；喻德旷等[8]在多事故点救援的最初阶段，为满足各灾点对多种物资运抵需求的紧迫性，与灾后道路状况的实时变化相结合，改进了遗传算法，提高了应急救援运输的效率；王杰等[9]针对海上环境的复杂性和远洋渔船补给资源的特点，以最小补给成本为目标函数，建立了混合时间窗下的惩罚成本函数，构建了资源补给船的航线规划模型。

在应对重大突发事件过程中，可能存在多个出救点和事故点，导致应急资源的调度过程复杂。不但要考虑应急资源调度的效率，还要考虑配送到达事故点应急资源的利用率，即事故点对配送到达资源的需求紧迫度。通过对各事故点进行优先级排序，最大限度利用配送到达各事故点的应急资源。已有学者就考虑救援优先权的应急资源调度优化进行了研究，张恭孝等[10]基于证据理论相关知识建立了救援优先权排序模型，用以解决多事故点应急资源调度的优先问题；Y.B.CAO等[11]基于谢菲尔德法，研究了事故点救援优先级的确定以及应急资源调度方案的制定问题；姚恩婷等[12]提出了基于BP神经网络的分级方法，直接针对各事故点的需求紧迫性进行分级研究，克服了评价过程中的主观性，并通过与其它评价方法比较，进一步验证该分级评价方法的合理性；J.B.SHEU等[13]和王东海等[14]运用TOPSIS模型评价各事故点的救援优先权，并将其转化为救援优先权系数加入到优化模型中；栾婷婷等[15]在改进传统TOPSIS法的基础上，针对各类应急资源在不同受灾点的供应优先级各不相同的特点，建立铁路应急资源供应优先级评价体系，以便科学合理的向各受灾点调度应急资源；王莉芳[16]综合考虑多个事故点的信息，构建受灾点应急物资需求紧迫性分级评价指标体系，利用灰色关联分析改进TOPSIS方法建立多事故点应急物质需求紧迫性分级模型，并通过熵权法和层次分析法相结合，确定各指标的综合权重系数；汤兆平等[17]把模糊评价法与基于熵值客观权重的灰色关联理想方法结合，对多需求点的救援优先级进行排序，建立了多出救点、多需求点、多资源的多目标优化模型。

国内外学者在铁路应急资源调度相关领域做了大量的研究，但对于优先权评估模型的设计比较单一，不能克服或消除专家主观的影响。多目标规划模型也都建立在时间最短、成本最少等目标上，没有结合优先权问题，对多事故点中优先救援的需求点因救援延迟造成的损失进行研究。笔者首先构建了铁路救援优先权评价指标体系，然后采用改进的层次分析法与灰色白化权函数聚类分析法来确定各事故点的救援优先权。在此基础上建立总调度时间最短、应急调度总成本最小、总惩罚成本最小的多目标优化模型，使应急资源调度的过程更具科学性和有效性，以期为应急救援科学决策提供有效地支撑。

1 救援优先权评价指标体系

当多事故同时发生时，初期应急救援基地存储的应急资源总量可能无法满足所有事故点的应急需求。首先需要对各事故点的受损程度进行分析，进行救援优先级排序，而评价指标体系的建立是事故点应急救援紧迫性分级的前提。影响铁路救援优先权评价的因素有很多，笔者在现有的研究成果基础上[14-16]，结合现场调研以及专家意见进行优化调整。当事故点发生地在桥梁或隧道时，将给救援带来巨大困难，同样事故点的天气情况也将影响救援进度，故在评价指标体系中加入了“环境因素”(天气因素和地形因素)。在“人员影响情况”中增加了“滞留旅客人数”这一指标，使铁路事故点救援优先权的评价体系更为全面、完善。最终建立了有2个一级指标、5个二级指标以及18个三级指标的铁路多事故点救援优先权评价指标体系，如表1。

表1 铁路多事故点救援优先权评价指标体系Table 1 Evaluation index system of rescue priority for railway multipleaccident points

用uz表示一级指标，用uzg表示二级指标，用uzgk表示三级指标，则准则层包括的一级指标因素集可表示为：

U={u1,u2}

(1)

子准则层包含的二级指标因素集可表示为：

U1={u11,u12,u13},U2={u21,u22}

(2)

指标层包含的三级指标因素集可表示为：

(3)

2 改进灰色聚类层次分析的优先级评价模型

2.1 确定各评价指标权重

2.2 铁路各事故点救援优先权综合评估

2.2.1 确立评价指标值矩阵

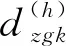
(4)

2.2.2 确定评价灰类及相应的白化权函数

灰色聚类分析法首先要确定观测指标和观测对象，而后利用灰数的白化权函数或关联矩阵将其分成若干可定义的类，从而用灰色聚类分析方法，对采用专家打分法得到的评价指标矩阵计算评分，实现对多事故点救援优先权的评估。灰类划分的详细程度可由评价指标的复杂程度决定，在2.2.1节中，根据评价准则对评价指标进行等级划分，将评估对象依据评价准则划分为5个灰类，评价灰类的灰数λ=5个，灰类序号为e=1,2,…,λ，相应的灰类及白化权函数式(5)～式(9):

(5)

(6)

(7)

(8)

(9)

2.2.3 各事故点救援优先权的综合评分

计算灰色评价系数以及灰色评价矩阵。指标层指标的灰色评价系数用ηzgke表示，ηzgk为指标层指标总灰色评价系数，rzgke为指标层每一个指标的灰色评价权重，rzgk为指标层每一个指标的灰色评价权向量，根据2.2.2节的白化权函数得到计算公式如下：

(10)

(11)

(12)

可计算出指标层指标的灰色评价权向量为：

rzgk=[rzgk1rzgk2…rzgkλ]

(13)

(14)

(15)

(16)

[Ez1…Ezg…Ezng]T

(17)

Π(ψ)=[E1E2]T

(18)

E=AΠ(ψ)=(a1,a2)×[E1E2]T

(19)

最后根据上述公式求得指标层、子准则层、准则层、目标层指标综合评分。Wzgk表示指标层评分，Wzg表示子准则层评分，Wz表示准则层评分，W表示目标层评分，计算公式为：

Wzgk=rzgkFT=rzgk×(5，4，3，2，1)T

(20)

Wzg=EzgFT=Ezg×(5，4，3，2，1)T

(21)

Wz=EzFT=Ez×(5，4，3，2，1)T

(22)

W=EFT=E×(5，4，3，2，1)T

(23)

通过比较各事故点的目标层评分，即救援优先权评分值W。W值越大，表示事故点的优先权越高，W值越小，表示事故点的优先权越低。

3 铁路多事故点应急资源优先级调度模型

3.1 问题描述

设集合C={Ci|i=1,2,…,m}表示备选的应急救援基地，集合G={Gj|j=1,2,…,M}表示突发事件发生地(应急资源需求点)，集合R={Rl|l=1,2…,ε}表示应急资源种类。救援过程中，因运力有限、时间紧迫导致应急资源储备量不能满足所有事故点的需求，必须科学判断各事故点的救援优先级，构建应急资源多目标规划模型，对各事故点展开科学、合理的应急救援。

3.2 模型假设

笔者设置的多目标优化模型有如下假设：

1)假设铁路事故发生后，铁路相关部门及相关人员可通过一定的技术手段及时获得事故现场相关信息，并预测出各事故点的应急资源需求量。

2)当铁路同时发生多起突发事件时，所需要应急资源总量会相对增加，假设现有铁路应急救援网点储存的应急资源量不充足。

3)每个应急救援基地Ci具有ζi辆规格相同的救援列车，具体数量根据救援基地等级而定。每辆救援列车均具有足够的装载与运输能力(即每个救援基地针对一个事故点只需要出动一辆应急救援列车)，所有救援列车均到达事故现场后，才可以开展营救工作，且各事故点的救援时间转化系数和各种类应急资源的单位惩罚成本，不会因应急救援开展时间的早晚有所变化。

3.3 模型构建

以总调度时间最短、应急调度总成本最小、总惩罚成本(某种类的应急资源未能及时得到满足时引起的进一步损失)最小为优化目标，建立应急资源调度优化模型。与单目标或者双目标调度优化模型相比，考虑更全面且较为合理的刻画出了多个突发事件同时发生时，救援初期应急资源量不充足的情形，并将各事故点的救援优先权以系数形式表达在目标函数中，达到根据各事故点救援优先权决定应急资源分配方案的目的。目标函数式w表示总调度时间最短、应急调度总成本最小、总惩罚成本最小的规划方案，引入单位时间转化成本系数θ，将时间目标转化为成本目标。优化模型如式(24)：

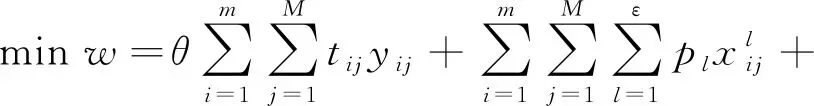
(24)

该模型的约束条件如式(25)～式(29)：

(25)

(26)

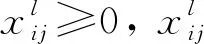
(27)

(28)

(29)

式中：i=1,2,…,m;j=1,2,…,M;l=1,2,…,ε。i,j,m分别表示应急救援基地数、事故点数和应急资源种类数的数量限制，即应急救援基地数量为m个，事故点数量为M个和应急资源种类数为ε个。

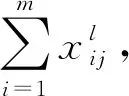
4 算例分析

4.1 问题描述

假设南昌铁路集团有限公司辖区内同时发生4起突发事件，根据案发现场相关人员反馈的信息整理出各事故点的具体情况如表2。需要的资源分别为：救援人员R1(专业指挥人员、消防人员、医护人员等)，救援工具R2(复轨器、千斤顶、索具等)，医用物资R3(消毒设备，防疫设备，医疗设备等)，食用物资R4(面包，方便面、饮用水等)，各事故点所需应急资源种类及数量如表3。通过ArcGIS软件计算得出6个备选的应急救援基地，其到各事故点的最短旅行时间如表4、应急资源存储的种类及数量如表5、现有的救援列车的数量如表6。

表2 各事故点(Gi)信息反馈表Table 2 Information feedback table for each accident point

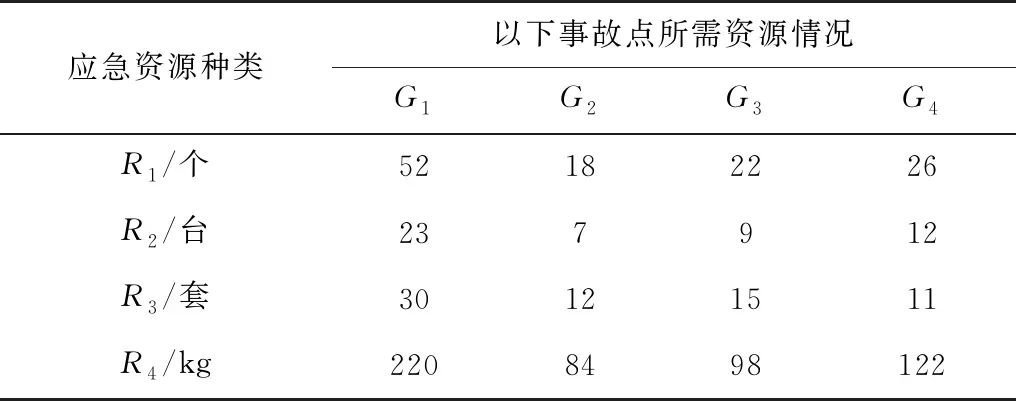
表3 各事故点所需应急资源种类及数量Table 3 Types and quantities of emergency resources required foreach accident point

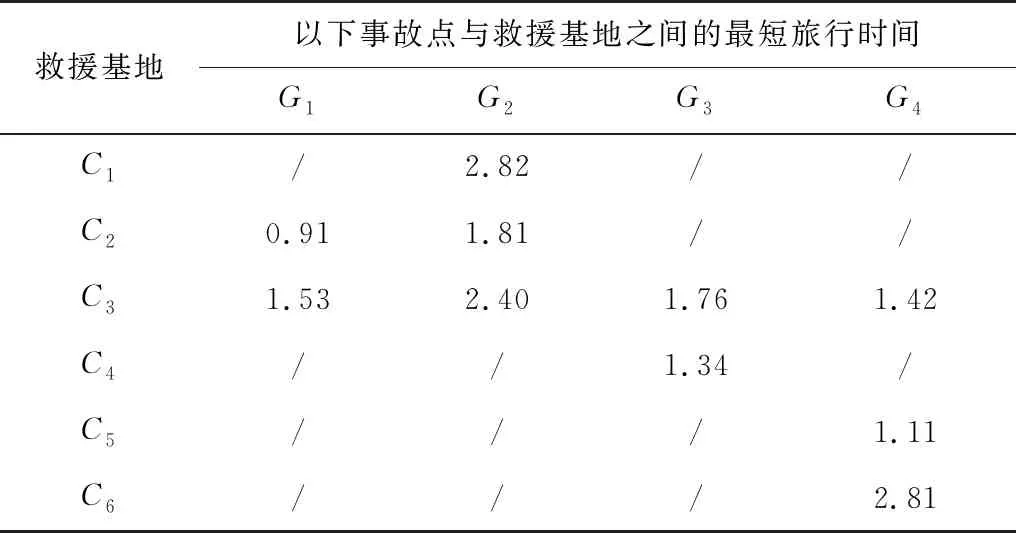
表4 各应急救援基地到事故点的最短旅行时间Table 4 The shortest travel time from each emergency rescue base tothe accident point h

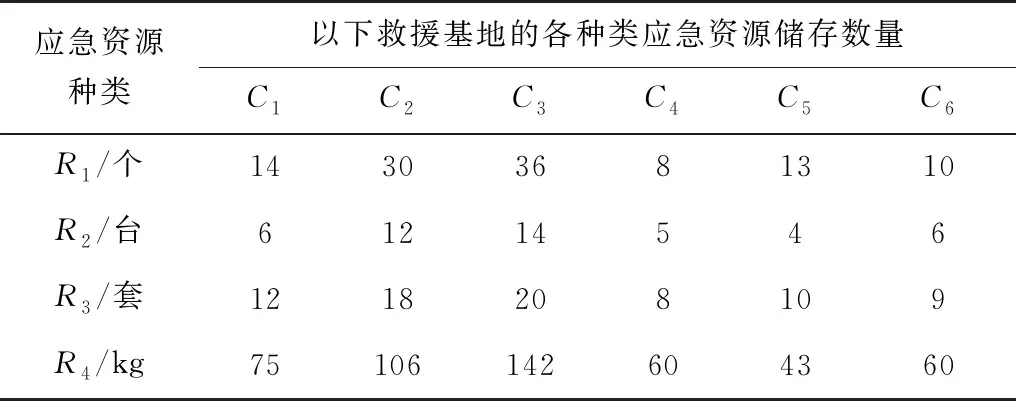
表5 各应急救援基地存储应急资源种类及数量Table 5 Types and quantities of emergency resources stored ineach emergency rescue base

根据该局应急救援基地现状，可知应急救援基地为特等站时有2辆救援列车，其余情况均为只有1辆救援列车，如表6。

表6 各备选应急救援基地的救援列车数Table 6 Number of rescue trains in each alternative emergencyrescue base 辆

根据铁路应急救援相关已有知识及救援原则，以及事故点所在地区的经济情况及消费水平，可得出不同种类应急资源单位调度成本及单位惩罚成本如表7。

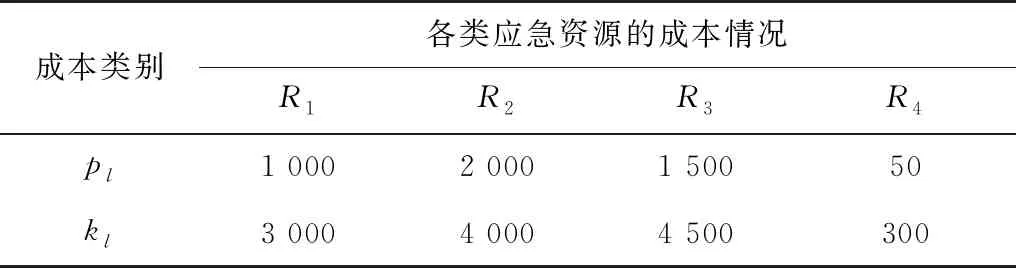
表7 不同种类应急资源的单位成本及惩罚成本Table 7 The unit cost and penalty cost of different types ofemergency resources 元

4.2 计算各事故点优先权

先选用改进的层次分析法计算各评价指标权重，并进行一次性检验，得到各个评价指标的权重；组织6位专家对各事故点的各指标进行独立打分，得到各个指标的评价矩阵如式(4)，通过灰色白化权函数式(5)～式(9)对各个指标进行逐一计算，得到每个指标uijk属于第e个灰类的灰色评价系数ηijke，再根据式(11)～式(13)得到指标层指标的灰色评价权向量rijk=[rijk1rijk2…rijks]，便可得到各个子准则层指标的灰色评价权矩阵，以G1的u12为例，其灰色评价权矩阵如下：

由式(16)～式(19)进一步得出准则层指标u1、u2所分别对应的灰色评价权矩阵和综合评价结果：

以及事故点1的目标层u对应的灰色评价矩阵Π(1)=[E1E2]T，和对应的综合评价结果E1=AΠ(1)=(0.349 2,0.322 2,0.224 2,2.526 3,0.028 3)。

同理可以依次计算得到4个事故点的综合评价结果E1、E2、E3、E4。最后根据式(20)～式(23)，分别计算得出其对应的综合评分为W1=8.2621、W2=3.037 4、W3=3.278 4、W4=3.576 0，因此各事故点的救援优先权依次为G1、G4、G3、G2。

4.3 模型求解与结果分析

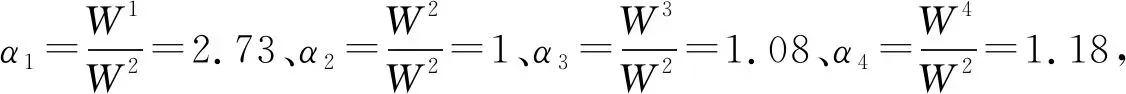
铁路多事故点应急资源调度模型属于线性整数规划模型，可运用MATLAB进行求解，采用遗传算法单点交配进行交配操作，并采用基本位进行基因突变。为防止种群过早收敛，对基因码实行小机率翻转，通过仿真和调试设置合理的相关参数为：遗传算法种群大小为20，进化迭代次数为100，交叉概率为0.75，变异概率为0.06，得到应急资源调度方案如表8。

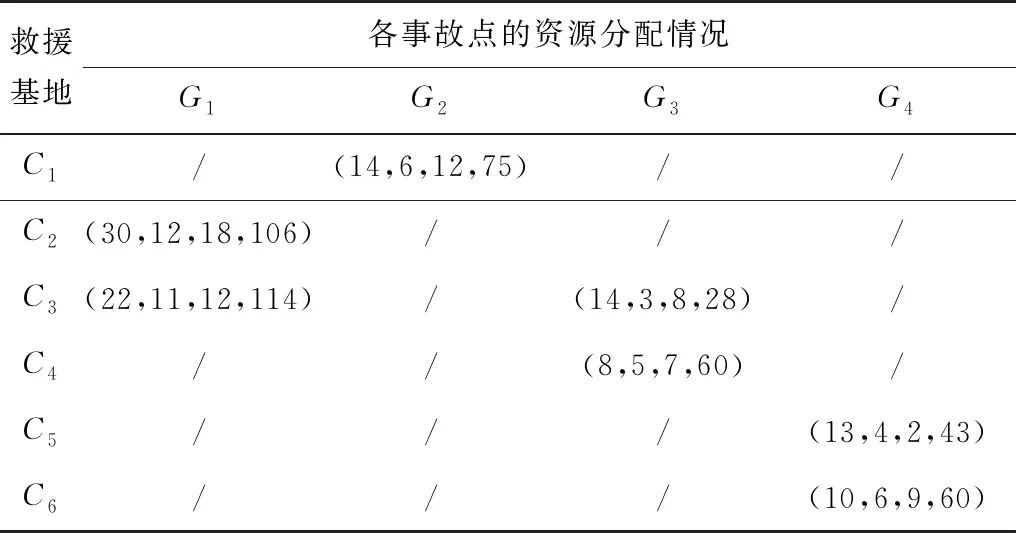
表8 考虑事故点救援优先权的铁路应急资源分配方案Table 8 A railway emergency resource allocation plan consideringthe priority of rescue at accident points

由表8可以看出：

1)参与事故点G1的应急救援基地有C2、C3,其中分得的R1类应急资源总量为52个；R2类分得23台；R3类分得30套；R4类分得220 kg。各类资源均无缺额。

2)参与事故点G2的应急救援基地只有C1，该事故点所分得R1类应急资源总量为14个，缺额为4个(与表3各事故点对各资源的需求量比较获得)；R2类分得6台，缺额为1台；R3类分得12套，该类资源得到满足；R4类分得75 kg，缺额为9 kg。

3) 参与事故点G3的应急救援基地有C3、C4，该事故点所分得的R1类应急资源总量为22个，无缺额；R2类分得8台，缺额为1台；R3分得15套，无缺额；R4类分得88 kg，缺额为10 kg。

4)参与事故点G4的应急救援基地有C5、C6，该事故点所分得的R1类应急资源总量为23个，缺额为3个；R2类分得10台，缺额为2台；R3类分得11套，无缺额；R4类分得103 kg，缺额为19 kg。

综上可见，事故点G1的救援优先权明显优于事故点G2、G3、G4，事故点G1惩罚成本为0，即所有应急资源均得到满足；事故点G2、G3、G4的救援优先权依次是G4>G3>G2，但救援优先权系数差别较小，因此出现事故点G4、G3、G2的各应急资源的未满足量差别较小，与计算结果符合。该分配结果表明：各事故点对资源的竞争和冲突得到解决的同时，还尽可能地满足了各事故点之间救援优先权需求。

5 结论

笔者考虑当多事故点同时发生、应急救援初期应急资源储备量不充足情况，对如何根据事故点救援优先权科学的分配应急资源、制定合理的多事故点应急救援方案进行研究。

1)通过系统的分析了突发事件救援优先权影响因子，构建了更为全面完善的救援优先权评估指标体系(包括定性指标和定量指标在内的18个不同的评价指标)，采用了改进的层次分析法对各影响因素权重进行分析，制定了评分准则，并运用了灰色聚类分析法计算评分，进而建立了适用于评价多事故点救援优先权的改进聚类层次分析模型，实现了对多事故点救援优先权的评估。

2)分析了应急资源调度具有多点对多点性、应急资源量不充足性和多目标性等特点。基于救援优先权的分配原则，构建了总调度时间最短、总调度成本最少和各事故点应急资源总惩罚成本最小的铁路应急资源调度多目标规划模型，并把已求解出的救援优先权以系数的形式引入到模型中，获得多事故点的应急调度方案。解决救援初期应急资源量不充足的情况下，铁路多事故点间应急资源的竞争与冲突问题。确保了优先权较高的事故点能够优先得到应急资源，最大限度减少灾害带来的损失。

3)以某铁路局辖区范围内线路为研究对象，进行算例分析，运用所构建的救援优先权评估模型确定各事故点的救援优先权，在此基础上构建了总时间最短、总调度成本最少和各事故点应急资源总惩罚成本最小的多目标规划模型，通过遗传算法求解出最优的调度方案，得到的救援优先权分别为G1>G4>G3>G2。