复合材料加筋结构剪切屈曲模态分析

2022-02-06吴晓阳陈青赵彬

科学技术与工程 2022年35期

吴晓阳，陈青，赵彬

(西北工业大学力学与土木建筑学院，西安 710021)

碳纤维复合材料加筋结构在生活中的各个领域应用越来越广泛，它在强度和模量方面比金属材料具有更加明显的优势。在结构设计阶段，基于复合材料韧性较差的考虑，设计者会使结构的设计载荷小于屈曲载荷。随着制造精度和加工工艺的改进，复合材料层合板的性能更加稳定。但是结构的稳定性一直是航空航天领域关注的重点。结构的非线性和不稳定性问题超出线弹性经典理论的解决范畴，因此，很难找到一种解析解对其进行准确描述。Yuan等[1]基于Buckingham’s Pi理论提出了一套适用于加筋壁板的压缩相似准则，并以复杂承载结构的基本单元加筋板为研究对象，深入分析了屈曲过程。

Singh等[2]观察到几何参数(长宽比)、纤维体积分数和编织角对编织复合材料层合板的屈曲响应有显著影响。Wang等[3]采用有限元法对轴向压缩载荷下加筋复合材料层合板的屈曲行为进行了详尽分析。Ambur等[4]、Anaisa等[5]通过试验和有限元方法分析了带切口和不带切口的复合材料加筋板在平面剪切荷载作用下的屈曲状态，并研究了两种结构的渐进损伤状态，弥补了该领域试验和理论分析的不足。Ma等[6]提出了一种简化的半解析方法来预测湿热环境下加筋板在剪切载荷作用下的临界屈曲载荷。邵青等[7]和冯宇等[8]采用了静力破坏试验方法研究了复合材料加筋板在剪切加载条件下的屈曲承载特性，对比了三种不同结构参数试验件的屈曲及破坏载荷。Guo等[9]针对复合材料工字型加筋壁板在轴压载荷作用下的屈曲和后屈曲行为，结合试验开展了有限元分析，计算出了结构的屈曲和后屈曲承载能力，并对壁板中关键部位的应变-载荷特性进行了分析研究。唐振南等[10]、王平安等[11]、杨德生等[12]使用有限元分析软件，针对复合材料加筋壁板进行线性屈曲及非线性屈曲分析，通过试验对屈曲临界载荷以及载荷-应变曲线进行验证。Zhou等[13]和Ferrerira等[14]针对筋条对复合材料加筋板屈曲和失效模式进行了详尽的分析，获得了筋条腹板长度、宽度参数对结构屈曲、承载能力和破坏行为的影响。Feng等[15]通过剪切试验得到了应变曲线和屈曲载荷，提出了一种新的理论方法，将等效刚度和后屈曲角引入到理论模型中，并对结构的屈曲和后屈曲性能进行研究。杨钧超等[16]和李真等[17]分别使用工程算法和张力场的方式对加筋壁板剪切屈曲载荷进行计算，并使用试验和有限元的方式对其进行核验，结果表明理论计算可快速计算出结构的屈曲载荷，但是偏保守。

现以典型飞机复合材料加筋板结构为研究对象，利用试验和有限元的方法对结构的剪切屈曲模态和承载能力进行分析，在有限元计算时将含夹具和无夹具模型的计算结果进行分析对比，旨在得到一种能准确反映结构屈曲承载力的计算方法，为相关的复合结构设计人员提供设计思路，减少试验，避免浪费大量的人力物力。

1 剪切试验

1.1 试验件介绍

图1 加筋壁板试验件Fig.1 Stiffened panel test piece

壁板试验件包含两根环向筋条和四根纵向筋条，外廓尺寸为980 mm×740 mm×60 mm。主要由蒙皮、加强片、环向筋条和纵向筋条组成，环向筋条截面形状为L形，间距为390 mm，纵向筋条截面形状为T形，间距为155 mm。试验件形貌如图1所示。试验件中心区域为考核区，大尺寸结构可以保证考核区域应变的均匀性和边界的真实性。四周为加载区，在蒙皮和夹具之间粘贴加强片可以降低试验件刚度突变所造成的影响。

蒙皮、纵向筋条为AC531/CCF800H碳纤维单层预浸料复合材料，加强片材料为玻璃钢，环向筋条为铝合金。蒙皮铺设方式为[45°/-45°/0°/-45°/0°/45°/0°/90°/-45°/0°/45°/90°]s，总厚度为3.36 mm，共24层。纵向筋条厚度2.8 mm，层数20层，铺设方式为[45°/0°/-45°/0°/90°/0°/45°/0°/-45°/0°]s。材料参数见表1和表2。

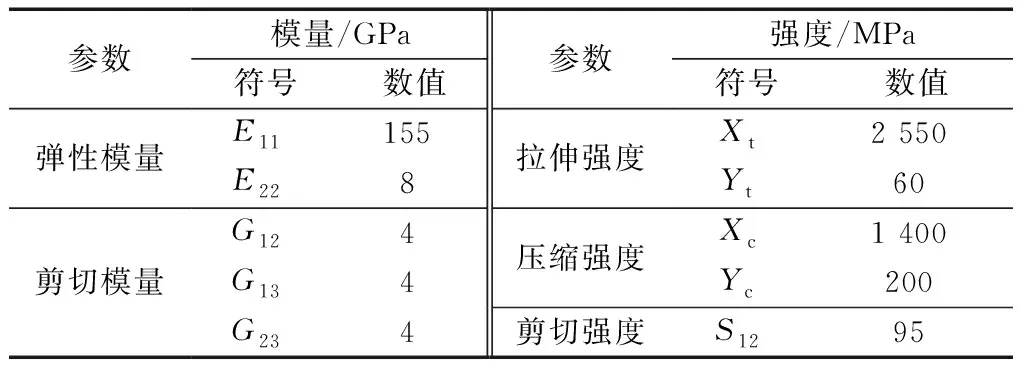
表1 复合材料参数

表2 其他部件材料参数

1.2 试验过程及结果

剪切试验使用万能试验机进行试验加载，在钢制夹具两相对的铰支点上施加拉伸载荷F，通过夹具与试验件蒙皮的连接，将拉伸载荷转化为试验件内的纯剪流，形成剪切载荷。加载示意图如图2所示。

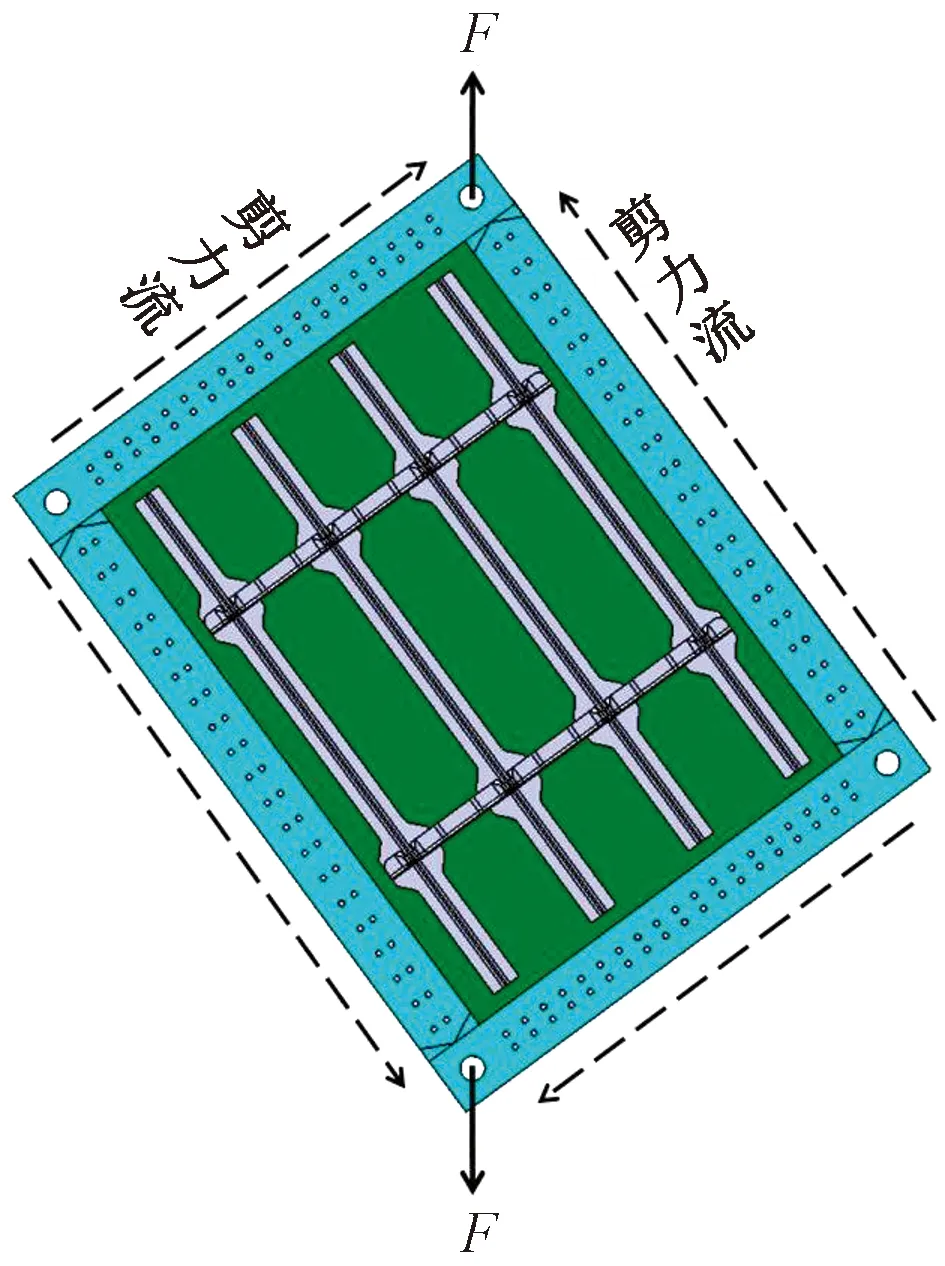
图2 加载示意图Fig.2 Loading diagram

①1/2/3(30/31/32) ②4/5/6(33/34/35) ③7/8/9(36/37/38) ④10/11/12(39/40/41) ⑤13/14/15(42/43/44) ⑥16/17/18(45/46/47) ⑦19/20/21(48/49/50) ⑧22/23/24(51/52/53) ⑨25/26/27(54/55/56)图3 贴片示意图Fig.3 Schematic diagram of strain gauge

试验件中心区域为结构考核区，中心区域正反面各粘贴9枚三向应变片用来监测蒙皮环向、纵向及剪切应变分布情况，粘贴位置及编号示意图如图3所示。其中通道1、4、…、25和通道30、33、…、54代表0°粘贴方向(平行于纵向筋条方向)，通道2、5、…、26和通栏和通道31、34、…、55代表45°粘贴方向，通道3、6、…、27和通道32、35、…、56代表90°粘贴方向(平行于环向筋条方向)。

试验件底部采用绞支的方式进行连接，可以使结构在受力过程中拉伸载荷充分转化为面内剪切载荷。试验采用载荷控制的方式施加在顶部绞支孔，在进行试验前需保证加载中心与蒙皮中面重合。在进行试验之前首先进行预试试验，小载荷预试试验可以有效消除结构装配之间的间隙，从而使试验件进入更好的试验状态。试验过程中采用摄像机记录整个剪切试验过程，载荷加载初始阶段，试验件无明显变形；继续增大载荷，试验件发出轻微响声，伴随着试验件中心部位发生明显鼓包，此时达到结构失稳状态；继续增大载荷，试验件破坏。试验件破坏形式主要有：蒙皮撕裂、纵向筋条与蒙皮之间脱粘及环向筋条断裂。剪切试验过程如图4所示。通过试验机输出载荷-位移曲线，如图5所示。

图5中曲线的斜率可以表征结构的刚度，载荷为518 kN时，曲线斜率发生微小变化，这表明结构的刚度在此刻发生了变化，对应剪切过程中的屈曲状态。载荷为631 kN时，曲线出现大幅度转折，结构丧失承载能力。曲线表明，当结构达到屈曲状态时并未丧失承载能力，而且结构屈曲失稳时结构的刚度变化不明显。

测试所得到的荷载-应变曲线如图6所示。由于试验件加载纯剪切载荷，环向和纵向在屈曲失稳前应变数值较小，而45°方向应变随载荷呈线性规律递增，1～27号应变曲线为试验件正面应变数据，30～56号为试验件背面应变数据。结构未达到屈曲状态时，正面和反面的应变数据重合，这表明加载中心与蒙皮中面重合，结构并未出现弯曲现象。当载荷达到518 kN时，曲线出现明显的分叉现象，且正反对称测量点呈现良好的对称性，说明加筋板发生屈曲失稳，传力路径发生改变。结合载荷-位移曲线和荷载-应变曲线可确定屈曲载荷为518 kN。当载荷为633.1 kN时，结构发生破坏，丧失承载能力。由此可知，屈曲载荷占破坏载荷的81.8%。

图4 剪切试验过程Fig.4 Shear test process

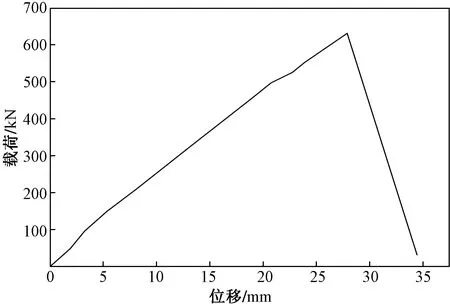
图5 载荷-位移曲线Fig.5 Load-displacement curve

图6 载荷-应变曲线Fig.6 Load-strain curve

2 有限元分析方法

在复合材料加筋壁板的设计阶段，采用有限元分析的方法可以极大地提高设计效率，可以避免理论分析所产生的复杂性和不确定性，同时能够及时发现设计中存在的不足。

2.1 屈曲模态的数值解

板、壳类型的薄壁结构达到屈曲状态时表现出复杂的非线性特征，很难找到解析解对其进行准确的描述。使用有限元离散的方法就可以很好地对真实情况进行模拟。屈曲状态的求解主要解决结构在载荷作用下产生的大变形和转动问题，此时材料仍处于线弹性阶段。将几何非线性问题进行离散，可使用载荷随增量步自动调节的方式进行迭代，形式为

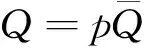
(1)

τKφ=0

(2)

τK=τKL0+τKL1+τKNL

(3)

式中：τ为屈曲时刻；K为刚度矩阵；下标NL为非线性相关的部分，下标L为线性相关的部分。对于屈曲失稳状态，上述非线性矩阵特征值求解可以通过载荷平衡的方式寻找解的区域，如果某个增量步的矩阵行列式乘积小于0，即

det(tK)det(t+ΔtK)<0

(4)

表明在该区域内有解，即

det(τK)=0

(5)

根据计算精度对矩阵进行进一步求解，将刚度矩阵进行三角化，即

t+ΔtK=LDLT

(6)

式(6)中：L为上三角矩阵，对角元素为1；D为对角矩阵，对角元素为dii(i=1,2，…，n)。由此可得

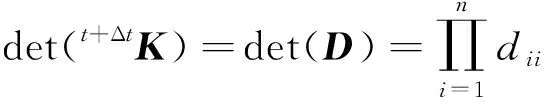
(7)

式(7)中：τK为t+ΔtK和tK之间的线性差。

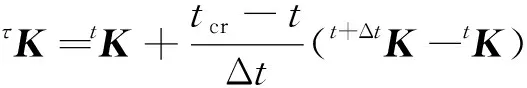
(8)

式(8)中：t为荷载水平或位移尺度；下标cr表示屈曲状态；Δt为增量步步长。将式(8)代入式(2)得到的特征方程为

[tK+λ(t+ΔtK-tK)]φ=0

(9)

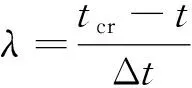
(10)

求解上述方程，可得到特征值λ1，λ2，λ3，…，以及对应的特征位移模态φ1，φ2，φ3，…。

2.2 有限元模型

使用ABAQUS商用软件构建有限元模型，为了节省计算资源，提高计算精度，将模型简化为壳单元进行计算。模型采用连续壳单元(S4R)进行模拟。为保证边界条件的真实性，蒙皮与横向筋条、加强片之间采用Tie约束，蒙皮与纵向筋条之间胶接界面采用黏聚力接触(cohesive surfaces)来进行模拟。为探究仿真计算中夹具对结构屈曲模态的影响，创建两种有限元模型，差异在于是否包含夹具。模型示意图如图7所示。

图7 有限元模型Fig.7 Finite element model

3 结果与讨论

使用有限元分析软件分别对两种模型进行屈曲载荷求解，本文中使用buckle分析步对两种模型进行剪切屈曲模态分析，模态分析结果如图8和图9所示。

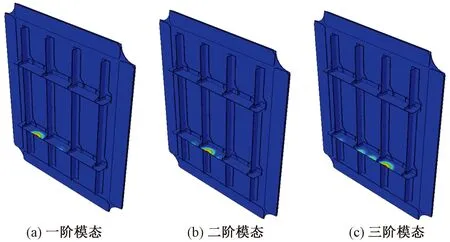
图8 无夹具模型屈曲模态Fig.8 Buckling modals of the without fixture model

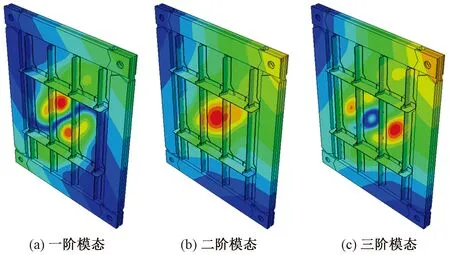
图9 含夹具模型屈曲模态Fig.9 Buckling modals of the fixture model

图8所示为无夹具结构的屈曲模态云图，从图8中可以看出，环向筋条出现了失稳区域，这是由于整个结构受到载荷作用时，边界刚度较弱，载荷主要分布于筋条上，且纵向筋条主要受到拉伸载荷，而环向筋条主要受到压缩载荷。对于长度方向远大于截面尺寸的结构来说，加强筋条对压缩载荷比对拉伸载荷更加敏感。

图9所示为含夹具结构的屈曲模态云图。当结构受到正向载荷时，受到夹具的影响，载荷优先沿着刚度大的区域进行传力，这就将拉伸载荷转换为剪切载荷。从图9中可以看出，壁板结构的失稳主要集中在中心区域，这与试验得到的屈曲形貌相同。相比于无夹具模型的屈曲模态云图，含夹具模型所得到的屈曲形貌与试验更为吻合，这就表明，在仿真模拟过程中，对于薄壁结构，边界条件会直接影响分析结果的准确性。

提取无夹具和含夹具结构的屈曲特征值，可以通过简单计算得到结构的屈曲载荷，屈曲载荷为特征值与加载载荷的乘积。计算后的屈曲载荷如表3所示。

由表3可以看出，有无夹具时，结构对于屈曲稳定性响应不同，且差异明显。在剪切载荷下，无夹具结构在153.05 kN时发生屈曲，而含夹具结构在527.56 kN处发生屈曲，两者相差3.4倍。试验测试得到的屈曲载荷为518 kN，与仿真计算时的含夹具模型屈曲载荷相对误差为1.8%。显而易见，在进行仿真模拟时忽略夹具可能导致严重的错误。值得注意的是，没有夹具的加筋壁板比有夹具的加筋壁板对荷载更敏感。夹具使整体试件的承载能力变得更强，因为夹具材质为合金钢，其刚度远远高于玻璃钢，在受力过程中承受更多的荷载。同时，对于力的传递路径，夹具的参与导致了结构边界增强，使得屈曲失稳区域发生在结构中心。

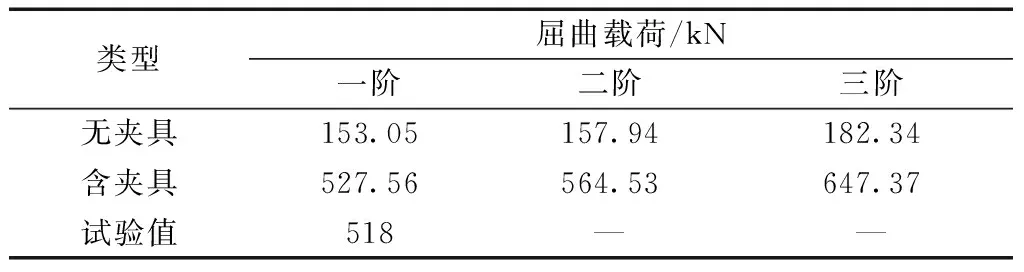
表3 屈曲载荷

结合试验和仿真模拟可知，本文所提出的有限元方法可以快速准确地得到结构的屈曲载荷，对比仿真模拟结果可知，边界条件的增强可以极大地改善结构的稳定性，这也为薄壁结构的设计者提供了良好的设计思路。良好的结构稳定性对于飞机结构非常有利，因为飞机结构在不同工况下的应力是不同的，希望一种壁板结构能够同时满足各种工况。