蜻蜓滑翔时三维串列柔性双翼气动效能分析

王玉平， 何心怡， 何国毅*， 王琦， 刘笑尘， 孙书美

(南昌航空大学飞行器工程学院， 南昌 330063)

作为自然界中优秀的飞行家，蜻蜓飞行的气动效能机理也一直为人们所关注[1]。不同于其他昆虫的飞行，蜻蜓可以凭借背腔上两对完美的翅膀轻松完成悬停、滑翔，甚至快速加速上仰等特技[2]。

得益于大展弦比、灵巧的飞行姿态以及超轻的重量优势，蜻蜓的飞行特性可为研究微型扑翼飞行器(flapping micro air vehicle, FMAV)所借鉴，而滑翔也是蜻蜓经常选择的飞的飞行方式[3-5]。一方面，由于高温潮湿等气候原因，蜻蜓飞行所损失的能耗不允许其频繁采用其他飞行方式[6]；另一方面，有学者认为蜻蜓可以利用滑翔完成体温调节等多类功能[7]。研究表明，蜻蜓最大的飞行速度甚至可以达到55 km/h[8]。在其短暂的一生中，通过滑翔的姿态，既可以达到低能耗飞行，又能够实现快速而精准捕捉昆虫。

滑翔过程中，蜻蜓双翅会产生不同程度的柔性变形[9]。这种变形是被动的，这是由于其翅翼表面几乎没有神经和肌肉方面的控制，很大程度上，变形由蜻蜓翼本身的材料属性及其运动过程中气动力的分布所决定，产生变形是十分自然的现象。目前，国内外对于蜻蜓翼运动机理研究较多，且取得了长足的进展，然而对串列双翼的流固耦合问题研究相对较少[10-11]。Lehmann[12]认为前后两翼相位的改变有助于推力的产生和机动飞行，通过计算分析，可以减少所需气动力的支出提高飞行效率。Wang等[13]用计算流体力学的方法研究了串列翼悬停干扰下的气动效能后认为：后翼在前翼的下洗速度场中运动，相互间的干扰使平均垂直力下降8%～15%。Zhang等[14]基于晶格玻尔兹曼方法研究了蜻蜓翅膀的二维刚性模型，得出双翼的有效排列可以提高总升力，降低机翼阻力。罗云等[15]利用数值模拟的办法，求解了蜻蜓翼滑翔时三维刚性双翼的气动特性，然而研究忽略了柔性变形等一些关键的影响因素。

基于文献[15]的基础之上，研究出一套双向流固耦合(computational fluid dynamic/computational solid dynamic，CFD/CSD)方法。对三维蜻蜓串列双翼模型进行必要的简化，改变雷诺数、滑翔迎角以及双翼不同的z向高置差，将柔性翼与刚性翼的运动效率对比分析。以Kesel[16]的实验数据为依据，研究杨氏模量一定(3 800 MPa)、泊松比为0.25时，三维串列柔性复翼在滑翔状态下的结构变形对空气动力的影响。由于双翼之间的柔性干涉在运动时可能诱导出多种复杂尾迹，前翼运动所产生尾迹将直接干扰后翼所处流场。研究前翼与后翼之间相位和间距变化对流场的影响规律，以获得更好的气动效能，这不仅对于更进一步揭示昆虫的飞行新机制，以及对研制新型FMAV都有一定的借鉴意义。

1 模型与方法

1.1 模型的建立与简化

需要指出，真实三维蜻蜓翼之间的排列并非是简单串列的，而同时存在着微小的翼间高置差，本文设置了6种不同差值(z向翼间距h=-0.6～1.8 mm)，固定后翼处于初始0平面位置，规定前翼在上为正值，调整前翼位置，如图1所示。

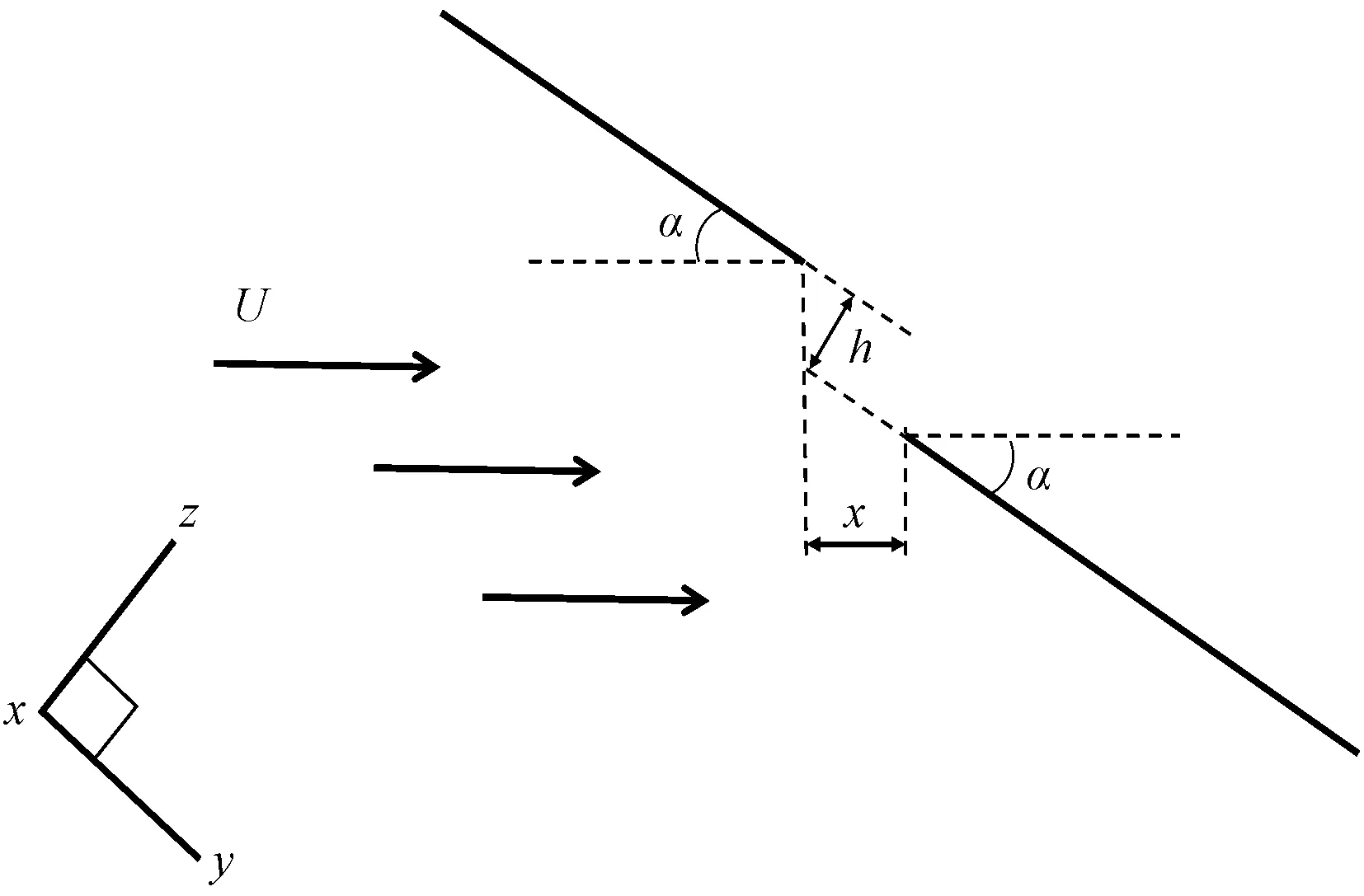
图1 双翼不同翼间高置差Fig.1 The difference in altitude between the wings

通过改变来流速度U、迎角α、z向翼间距h，研究被动变形能否平衡上下翼面的压力差；弦向翼间距方面，根据Luo等[17]的结果，这里固定双翼间距x为4 mm不变。

三维建模软件CATIA在逆向仿生工程方面有着显著的技术优势，利用样条曲线功能拟合出三维串列蜻蜓翼外轮廓，填充轮廓便得到由轮廓包围的几何结构。同时，考虑到微结构在双向流固耦合求解时对计算资源要求十分苛刻，故先采用具有相同外形轮廓的平板结构代替，描绘的几何模型如图2所示。串列双翼的相关尺寸、材料参数如表1所示。

模型根据实际的特征做了必要的简化。

(1)不考虑翅痣、翅结等微小结构对气动特性的影响。

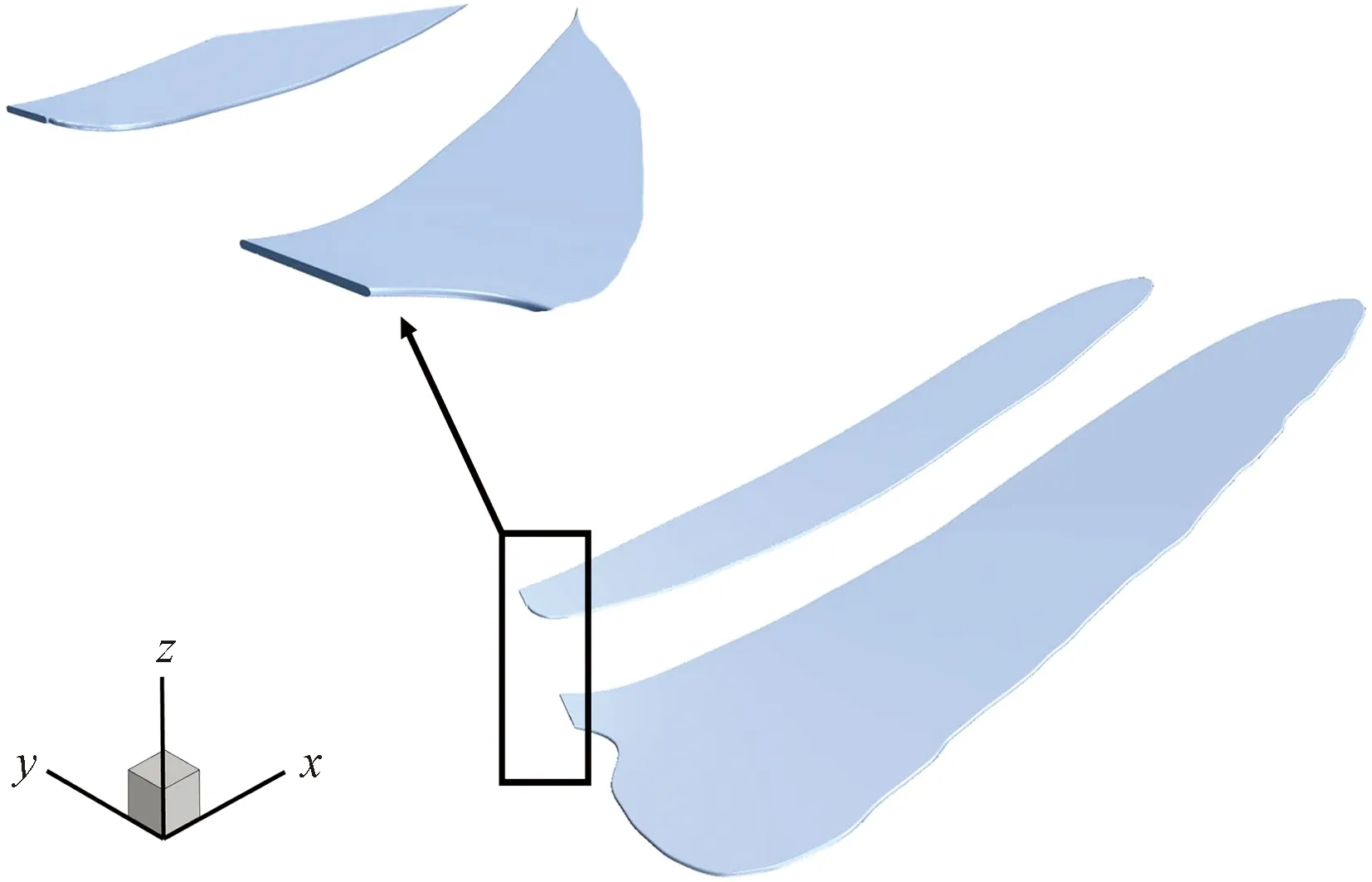
图2 蜻蜓翼三维模型Fig.2 3D model of dragonfly wings

表1 串列双翼参数

(2)不考虑翅翼尺寸沿弦向和展向的变化，模型统一采用厚度为0.18 mm的对称平板。

1.2 控制方程

流体域选择隐式非稳态、Shear-Stress Transport-K-Omega的二方程湍流模型；固体域为隐式非定常有限元固体应力模型。流体域提供外载荷，蜻蜓翼提供计算所需的运动边界，二者之间的双向流固耦合遵循基本的守恒原则，即

nfτf=nsτs

(1)

df=ds

(2)

式中：n为接触表面的法向单位向量;τ为应力；d为位移。二者之间的交界面充当桥梁的作用，完成力与位移的插值与映射[18-19]。由于蜻蜓翼的尺寸较小，因而飞行时的雷诺数对较低，一般为102～104。这里采用数值求解三维不可压Navier-Stokes方程的办法，并给出雷诺数及升、阻力系数的求解公式，即

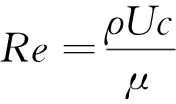
(3)

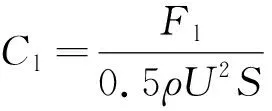
(4)

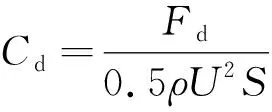
(5)

式中：ρ为来流密度；U为来流速度；c为平均几何弦长；S为翅膀水平投影面积；μ为动力黏性系数；Fl为升力；Fd为阻力。

1.3 计算流域与边界条件

建立的计算域如图3所示。其中，外流域y+、z-方向为速度入口，z+、y-为压力出口，流域右端为壁面，为充分调用计算资源，将翼根附近平面(左)设置为对称平面。

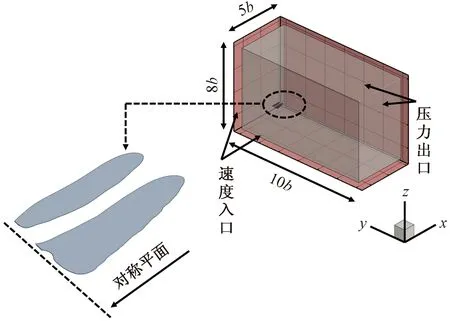
图3 计算流域与边界条件Fig.3 Calculate region and boundary conditions

1.4 网格无关性验证

滑翔速度v=18 m/s，迎角α=15°时，对外流域采用三套多面体网格划分策略，尺寸分别为0.02、0.03、0.04 mm三种，网格数量均基本稳定在178万左右，计算结果显示，流体域网格在0.03 mm时与前后者的误差分别在4.1%、3.9%，精度均在可接受的范围内，这里流体网格选择0.03 mm。

滑翔速度v=18 m/s，迎角α=15°时，对蜻蜓翼选择四面体网格划分，计算显示网格为0.03 mm时与前后者相对误差分别为0.6%、0.8%，考虑计算的最大效率以及仿真的精确性，这里固体网格选前翼网格为53万、后翼网格为68.9万，最终确定的网格如图4所示。

图4 三维网格模型Fig.4 3D mesh model

2 结果与分析

2.1 串列双翼的柔性变形分析

雷诺数一定(Re=104)时，计算不同迎角下，蜻蜓翼的柔性变形，如图5所示。

由图5可知，在小迎角下，前翼承担了主要的变形，其中前翼翼梢的变形量达到10 mm以上；迎角α=25°时，后翼的柔性变形要大于前翼，当来流Re=104时，后翼的变形增大达到16 mm，前翼面则发生了改变。迎角10°以前，蜻蜓翼依靠前翅完成主要的滑翔任务，迎角10°附近以后，后翼承担了大部分的载荷作机动飞行。

如图6所示，速度一定时，双翼的变形量总体趋势都在增加，然而后翼的增幅要略强于前翼；迎角一定来看，后翼翼梢点的变形始终在增大，前翼翼梢点在10°～15°时的变形量下降，随后变形缓慢增大。

图5 双翼柔性变形云图Fig.5 Contours of flexible deformation of wings

图6 不同速度与迎角下翼梢点位移变化Fig.6 Wing tip displacement changes at different speeds and angles of attack

扭转角方面[20]，在蜻蜓翼距离翼根20、30 mm处分别设置两组不同的监测位置，通过8个监测点的空间函数位移变化关系，给出串列双翼的扭转变形规律，如图7所示。

这里规定，蜻蜓翼在发生弯曲扭转后，绕双翼展向逆时针时的扭转为正，顺时针产生的扭转为负。

如图8所示，当蜻蜓在大迎角(α=25°)下滑翔时，双翼均会产生不同程度的扭转变形，且后翼的扭转程度要大于前翼；在v>9 m/s以后，后翼的扭转发生了突变，速度达到v=18 m/s时，扭转角达到最大。需要指出，此时蜻蜓翼的扭转并不总是朝着一个方向的。速度一定时(v=18 m/s)，前翼的两组监测点在迎角为10°以前均发生了顺时针方向的扭转，且距离翼根的扭转变形要略大，10°以后接近15°时，扭转朝着逆时针方向开始增加，且变形程度增加缓慢，没有出现滑翔时前翼大幅度变形的现象，而仅有后翼的扭转变形随着迎角与速度的增大而不断增大。

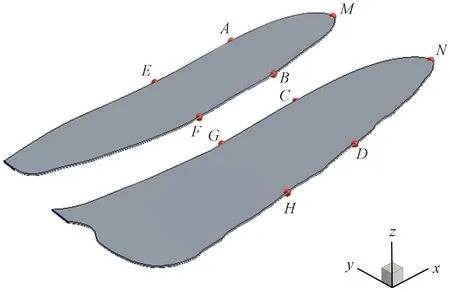
图7 监测点的布置Fig.7 Layout of monitoring points

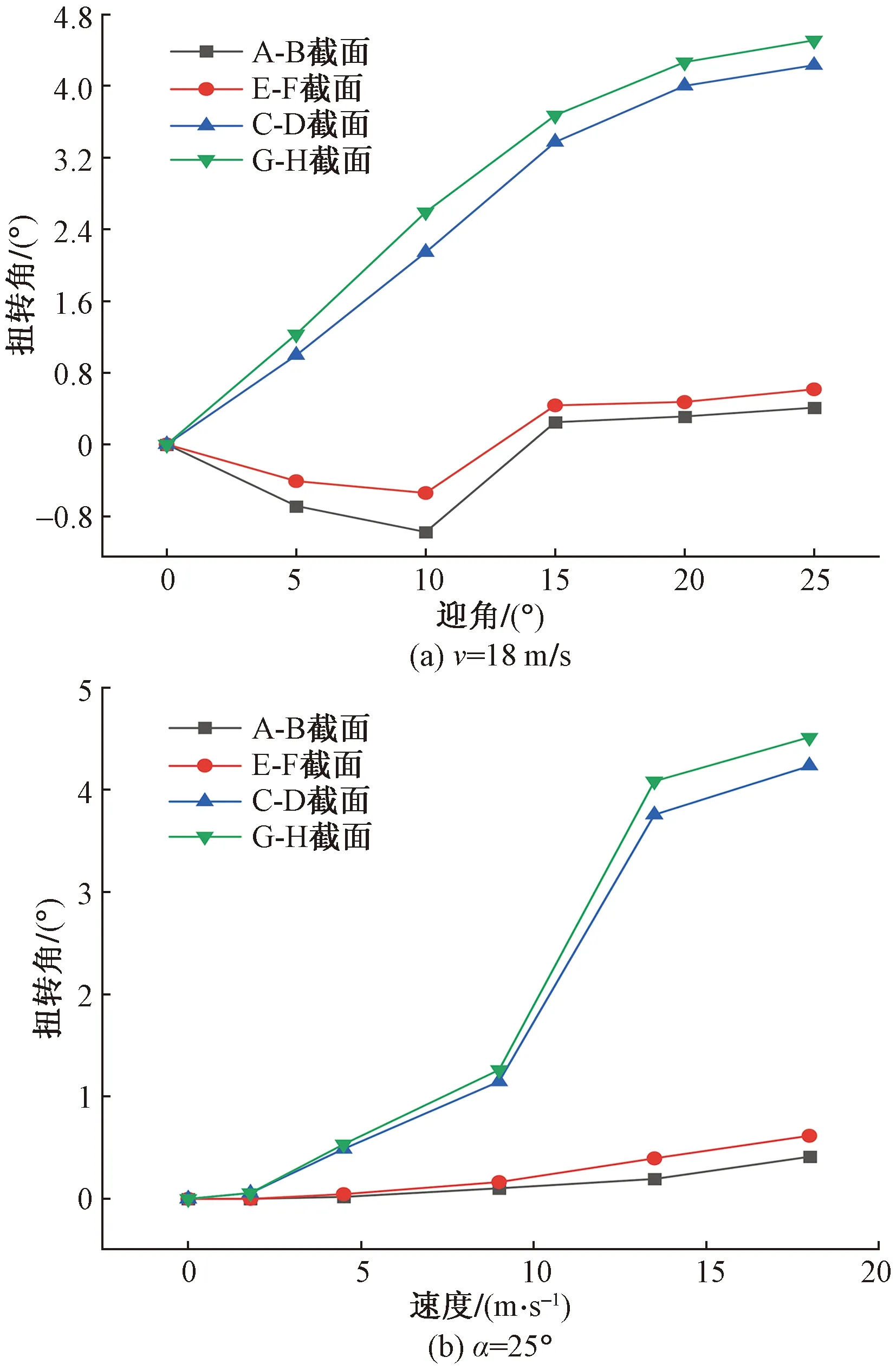
图8 不同速度与迎角下扭转角变化Fig.8 Variation of torsion angle at different speeds and angles of attack

2.2 不同高置差下，串列双翼的气动效能分析

雷诺数一定时(Re=104)，对6种高置差布局方式进行了分析，其中，一组为前翼在下的低置布局，5种前翼在上、后翼在下的高置布局方式。探究迎角在0°～25°时蜻蜓翼滑翔飞行的气动特性，如图9所示。

图9 v=18 m/s时不同高置差下的气动特性Fig.9 Aerodynamic characteristics under different height with v=18 m/s

升力系数方面，5种正向布局的方案都呈现出趋势相接近的结果。相对来说，前翼低置布局的排列效果则不如。尤其在迎角为5°时，升力系数比1.2 mm的高置布局方式低了5.2%，随着迎角的增大，差值也越大越大，迎角为25°时，达到19%。

正向的串列布局方式较于低置布局方式能更好利用大迎角下前缘分离的三维涡来改善流体的流动状态，提供可观的升力支持。这种干扰耦合减小配平阻力的同时也有利于短距起降。结果显示，高置差在0、1.2 mm时气动效能最为接近，且 1.2 mm 布局时的气动效能要略优于前者。本文中选择高置差为1.2 mm的模型进一步研究，与刚性翼的运动效率展开对比。

2.3 柔性翼与刚性翼的气动特性对比

迎角α=25°，将三维串列柔性翼与刚性翼的气动特性做对比，如图10所示。

图10 α=25°时不同速度下的气动特性Fig.10 Aerodynamic characteristics under different speed with α=25°

从图10可以看出，迎角一定、来流不同的情况下，虽然柔性翼升力系数的值低于刚性翼，然而其阻力系数的值也更低；不同于小迎角时，此时刚性前翼的Cl、Cd均随速度的增加呈现出先增后减的趋势，刚性后翼的Cd、Cl依然缓慢增加；单从升力特性来看，柔性翼均不如刚性翼的表现。需要指出，柔性后翼的阻力系数从v>9 m/s以后衰减的较快，从升阻比来看，v=18 m/s时，柔性后翼比刚性后翼的升阻比增大16%。根据张志君等[21]对5种不同翼型的研究表明：NACA8418和S1223-RTL翼型运动产生的强涡有助于推力的增加(阻力减小了)。由此确定柔性翼相较于刚性翼，其推进效率得到了提升。

2.4 串列柔性双翼的气动效能

如图11所示，流速一定的情况下，复翼的升力系数总体趋势均随迎角的增大而增大。且前翼的升力系数在各个来流、迎角下均大于后翼。

迎角一定时，前翼在18 m/s时展现的气动效能要优于大部分滑翔速度，而后翼的有利滑翔速度梯度范围在4.5～9 m/s；随着雷诺数不断增大，前后翼的阻力系数均不断减小，如图12所示。

图11 柔性翼升力系数随迎角变化Fig.11 Lift coefficient of flexible wing varies with angle of attack

如图13所示，前翼在迎角为5°～10°滑行时，升阻比能得到较好的维持，可以认为10°～15°的迎角范围是后翼滑翔的优势区。

迎角一定下，后翼的升阻比均随速度的增加而增加。这是双翼动态柔性干涉下的结果。

如图14所示，前后翼有一定的弦向间距(4 mm)，犹如一个开缝襟翼，流过开缝的气流可以控制后翼的分离，“襟翼”的存在，又可使前翼的环量增加。大迎角下，蜻蜓后翼在前翼诱导的下洗速度场中运动，降低了其空气动力。串列翼在保持气动特性几近相同的衰减趋势下，后翅阻力特性衰减则显得较为明显。

计算了不同迎角下的蜻蜓翼表面压力区变化，如图15所示。

蜻蜓翼前缘脱体涡的产生也正是由于上下翼表面形成的压力差。双翼下方的流动有在翼前缘发生绕流的趋势，而流动在翼尖前缘无法继续维持，气流分离形成剪切层，既有沿蜻蜓翼展向的分量又有沿弦向发展的分量，在后翼上方形成稳定较强的涡，因而提供可观的升力。

如图16所示，随着攻角的增大，双翼产生了不同程度的后缘涡，后缘涡的存在，对于延迟蜻蜓翼失速、控制气流分离有着明显的作用；后翅的涡明显强于前翅，这说明在动态柔性变形中，阻力的抑制作用也愈加强，在升力增加不明显的情况下，后翼的升阻比便得到了明显的提升。

图12 柔性翼阻力系数随迎角变化Fig.12 Drag coefficient of flexible wing varies with angle of attack

图13 柔性翼升阻比随迎角变化Fig.13 Lift-drag ratio of flexible wing varies with angle of attack

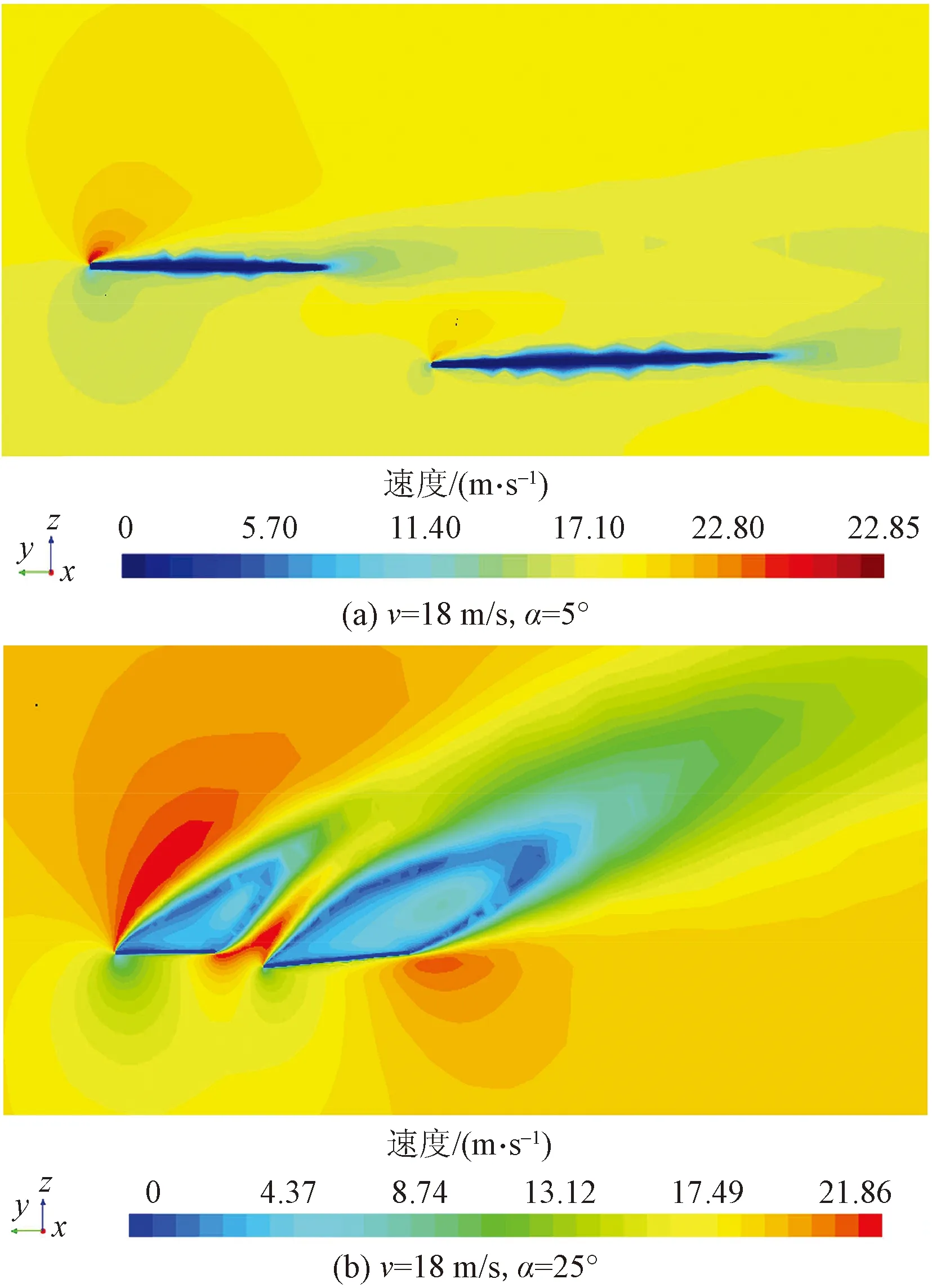
图14 速度云图Fig.14 Velocity contour

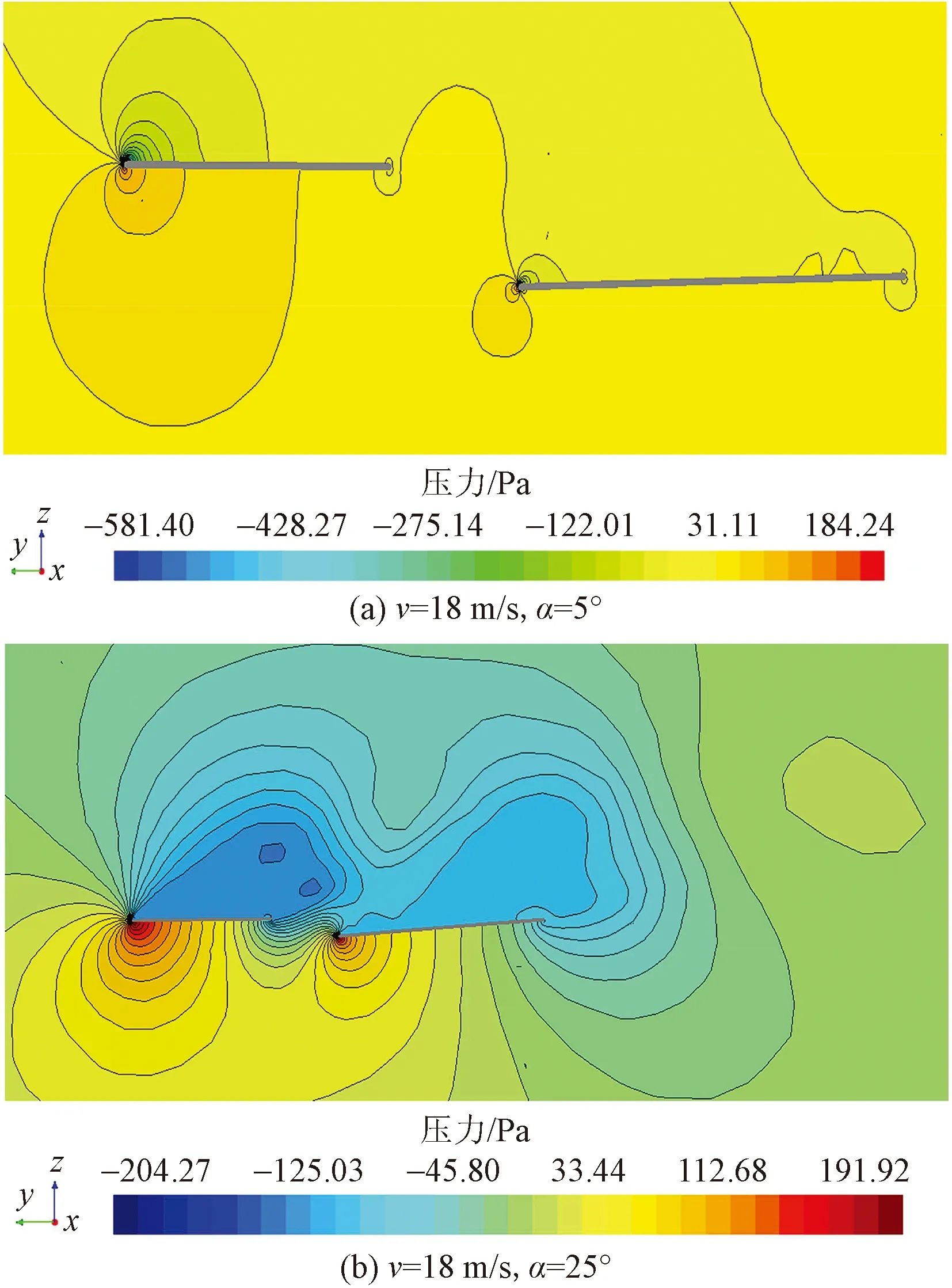
图15 压力云图Fig.15 Pressure contour

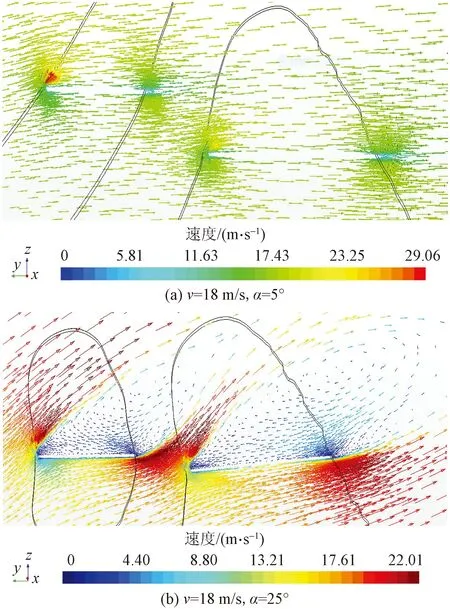
图16 速度流线图Fig.16 Velocity flow diagram

3 结论

对三维柔性蜻蜓串列双翼滑翔状态下的气动效能进行分析，得出的如下主要结论。

(1)蜻蜓串列双翼在气动力的作用下会产生明显的弯曲扭转变形。动态变形，相当于改变了两翼周围的流场结构，其趋于稳定的这个过程中，前翼尾迹对后翅来说是不利的，降低了其气动特性。相反，后翼的存在大大提升了前翼的气动效能，从整体效果来看，耦合干扰对于蜻蜓机动飞行来说是利大于弊。

(2)小迎角滑翔时，未发生明显的气流分离现象，不同于后翼，前翅的升力系数缓慢增加至平稳，后翅的升力系数则随速度的增大而减小；大迎角时，虽然柔性翼的升力系数不如刚性翼，但是其阻力系数的值也愈低，表现结果却更加贴近真实飞行。特别地，后翅的升阻比在9 m/s以后发生了突跃，这对于蜻蜓长时间滑翔后利用后翅承担载荷、机动飞行的观点增加了印证。

(3)扭转程度方面：大迎角下，蜻蜓翼的扭转角随速度的增大而增大，后翅的扭转程度要明显强于前翅；大速度飞行时，这个结论依然成立。前翅在小迎角下会发生顺时针方向的被动扭转，产生负的扭转角，起到了类似减速板的作用。

(4)蜻蜓滑翔时，蜻蜓翼的上表面的负压区随着迎角的增大而增大，逐渐向后移动；且在25°时，发生了较为明显的气流分离现象，蜻蜓翼上表面出现了顺时针的后缘涡。此时蜻蜓气动力的变化不仅仅是迎角单一作用的结果，而应考虑气流分离下后缘涡共同作用的情况。