终端区场景下空中交通流建模与控制分析

2022-02-06朱承元张澈管建华

科学技术与工程 2022年35期

朱承元，张澈，管建华

(中国民航大学空中交通管理学院, 天津 300300)

随着中国经济的持续稳定发展，航空运输市场的需求量不断扩大，在航空流量密集的区域，空中交通拥塞逐渐增多，不仅严重地威胁飞行安全，而且导致了大量飞行延误，对中国民航发展造成了巨大经济损失。在保持现有资源的条件下解决这一问题的有效途径之一就是对空中交通流量实施控制。尽管一部分空中交通阻塞可能是由于容量不足造成的，但是在航空领域有这样的一种共识，即这些问题可以通过更好的空域管理来解决。为了更有效地管理空域资源，研究者逐渐开始侧重于发展空中交通分析和管理工具，开发高保真度的空域仿真模型是这项研究的重要组成部分。由美国航空航天局开发的未来空中交通管理概念评估工具(future air traffic management concepts evaluation tool,FACET)和它的衍生物正是这方面研究的成果。尽管对于某些空管领域中的应用，使用空域中航空器级的模型是必须的，但是这种详尽全面的模型并不完全适用于交通流量管理问题，因为在这类模型中一架航空器的动力学方程至少需要三个微分方程来表达，导致问题的维数过大难以操作和计算。因此，低阶且高保真的空域模型是研究者所期望的。

针对空中交通流建模，杨磊等[1]根据空中交通流广义属性，将空中交通流模型分为“以流为中心”和“以人为中心”两类，对各类广义交通流模型的核心概念、建模方法和适用范围进行评述。Lighthill等[2]将行驶在道路上的群体车辆视为连续流体介质，提出了流体动力学模拟理论，建立LWR(Lighthill-Whitham-Richards)交通流连续性方程，分析交通流拥堵-传播-消散过程。Sun等[3-4]采用基于连续时间和空间的LWR偏微分方程建立国家空域网络空中交通流模型，采用相互联结的一维线元表示空域中的航路航线网络,用偏微分方程组解决交通流在网络中的传递问题。Menon等[5]通过对LWR方程进行时空离散处理，首次提出空中交通流一维元胞模型，并引入现代控制理论对模型的可控性、相应特性和稳定性进行分析,能够较好地的解决扩散性问题。张洪海等[6]和许研等[7]基于系统动力学推演方法建立一维元胞传输模型，对终端区进离场交通流流量-密度-速度三参数关系进行研究，具有较高的计算效率。Menon等[8]和Bai等[9]首次将一维交通流模型拓展至二维平面中，将空域按照1度经纬度等额递增离散正方形面元，通过恒速交通流在不同面元间的转换来表示空中交通的改航，更贴近实际交通流的运行情况。

针对栅格化空域, 程承旗等[10]以等度、等分、等秒的剖分网格为基础, 建立适合协调空地联合行动的网格体系, 设计了简单实用的定位编码方法, 对空域进行栅格化表征。徐鑫宇等[11]针对经纬度坐标表征空域描述复杂、无区域特征的不足，提出基于改进GeoSOT网格的空域栅格化表征方法，弥补了传统经纬度坐标表征方法烦琐复杂的缺点。

航空运输发达的国家和地区已经大规模地开展了有关空中交通流量管理理论问题方面的研究，以上所述模型均有相应的控制方法和寻优算法。随着中国军民航空中交通运输量的持续增长，空中交通流建模以及流量控制的重要性不言而喻。综合分析现阶段国内外交通流系统建模研究现状，中国学者主要致力于空中交通流一维元胞模型，此类模型的重要假设是严格遵循现有航路航线飞行，随着灵活航路的推广，若想更为全面地反映交通流的运行状态，则需要一个更灵活的二维空中交通流建模框架，因此二维控制体模型(2D menon model, MM2D)模型的二维元胞特点符合要求。传统MM2D模型将交通流视为恒速流，然而终端区进离场航空器速度变化较大且范围较小，若按1°经纬度离散，控制体个数较少，模型精度低，因此现权衡地理范围离散目标空域以及各二维面元中交通流平均速度，建立终端区场景下MM2D模型，并对模型进行稳定性、能控性以及最小控制量组合的分析。

1 MM2D模型

1.1 空中交通流概述

空中交通流是指空域的某个时间段运输网络内运行的航空器所形成的交通流。构建的MM2D模型是基于连续的稳态流，即航线上的航空器数量小于航线上节点的容量，航空器平稳运行。交通流特性可用交通流量、速度和密度三个参数来描述并分析交通流的变化规律。

其中，交通流量表示交通流在单位时间内通过路线指定断面的载运工具的数量(架/分)；速度表示交通流流动的快慢(km/h)；交通流密度表示交通流的疏密程度，指路线单位长度上含有载运工具的数量(架/km)。

如果考虑同一航路长度L、时段T，航空器架数n，其中三要素的相互关系为：交通量q=n/T；速度v=L/T；交通密度K=n/L。对于航线飞行而言，航空器飞行速度v通常视为确定值，因此针对区域管制空域的交通流建模而言，重要的是交通量与密度之间关系。对于终端区空域中进离场交通流而言，在进近管制移交空域和目的地机场间速度变化较大，速度变化量往往在200 km/h以上，需要对平均速度进行分段处理。

1.2 空域栅格化与二维面元信息的获取

空域的栅格化是MM2D模型建立的前提，相较于传统的基于经纬度坐标表征空域的方法更有效地利用信息资源。在Menon等[8]和Bai等[9]提出的二维欧拉模型中，每个正方形栅格均视为一个二维面元(surface element, SEL)。基于确定的SEL几何形状，对目标空域离散化处理，栅格化的填充处理过程如图1所示，二维面元SEL(i,j)的数字变化是：j自左至右增加，i自下至上增加，即等量增加经纬度。

连接各SEL的中心点和各边中点与顶点可获得8条交通流，即各SEL的8个交通流状态，如图2所示，其中(i,j)确定二维面元的位置，x代表在任一给定时刻一个交通流中航空器的数目。一个交通流中航空器的数目是关于时间的函数：x(kT)(k=0,1,2,…)，其中T表示时间间隔。

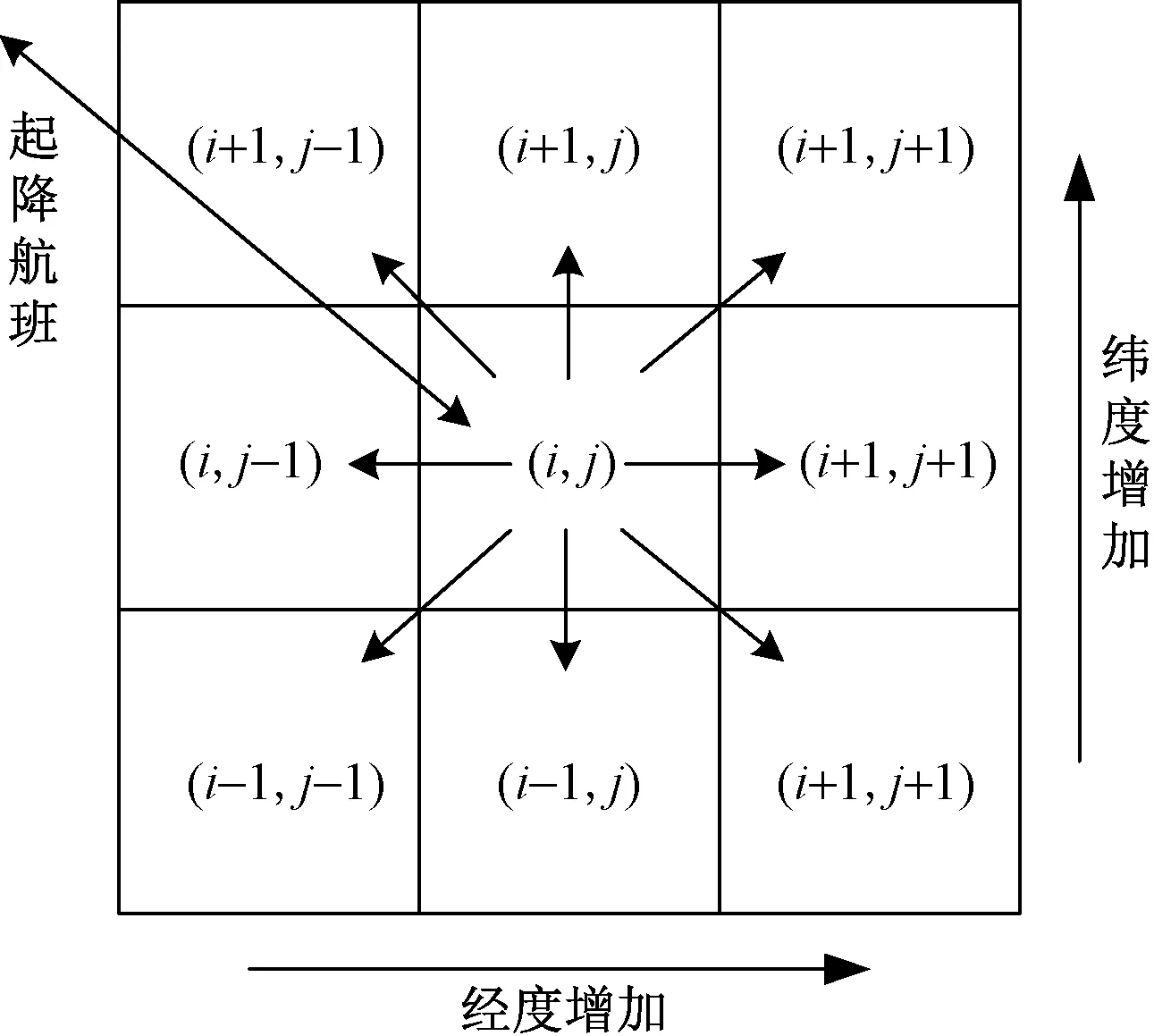
图1 栅格化填充过程Fig.1 Rasterization filling process

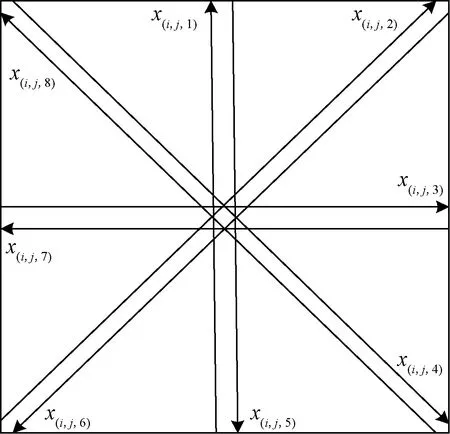
图2 二维面元交通流状态变化命名Fig.2 Name of state changes of two-dimensional surface element traffic flow

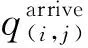
图3 特殊位置二维面元的输入Fig.3 Input of two-dimensional surface element in special position

1.3 MM2D模型参数

在MM2D模型中，如果航空器进入一个SEL，则有8个可能的方向流出，因而存在不同流向之间转换。这些交通流流向的变化在模型中可由流量分离参数βmn表示，即从流n中进入SEL后，从流m或到达流qarrive中流出的百分比。因此，对于一个SEL，所有的分离参数相加为1，即

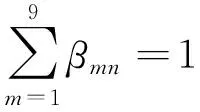
(1)

若航空器在某一SEL中始终保持在一个流中，则

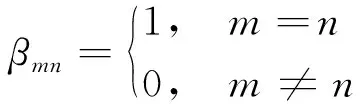
(2)

考虑终端区实际飞行情况及标准进离场飞行程序结构，排除航空器在同一个SEL中不存在反向飞行的可能，某些参数可默认为0。一个SEL中的交通流的状态变量x的状态变化，可通过总的输入输出流来描述。一些航空器在给定的时间段内，可能不会飞出其所在的SEL。因此，参数a(i,j,m)表示交通流驻留比率，代表由于元素尺寸或航空器速度的不同，在给定的时间段T内，没有飞出SEL的航空器占航空器总数的比率。当目前没有航空器时，它的默认值是0。控制变量u(i,j,m)表示管制员对SEL(i,j)中m方向交通流施加的控制量。

1.4 空域状态方程

对于二维面元SEL(i,j)，以方向1交通流为例，其空域状态方程表示为

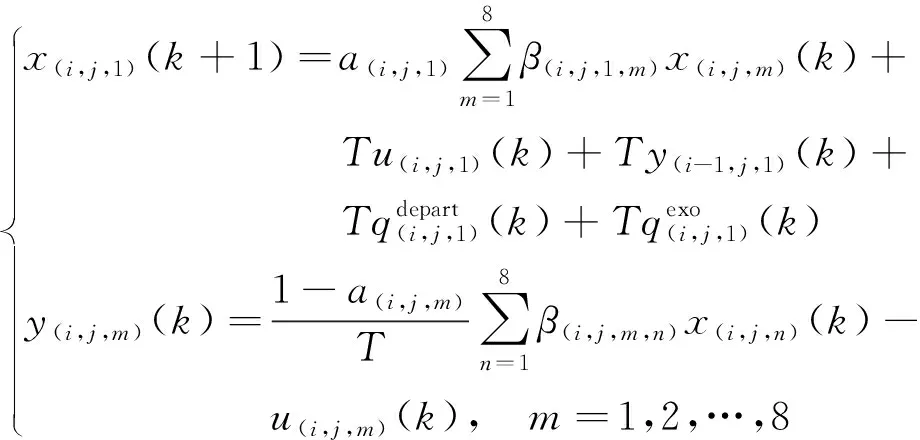
(3)

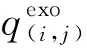
(4)

综上，空域状态方程能简洁的表达为

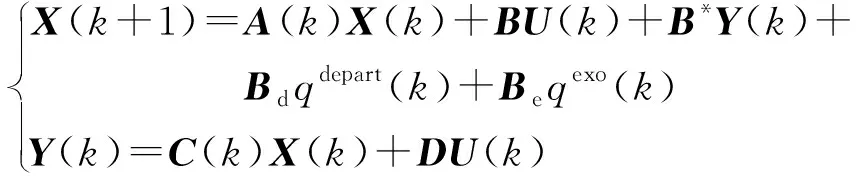
(5)

(6)

式中：A(k)为系统矩阵；B、B*、Bd、Be为控制矩阵；C(k)为输出矩阵；D为前馈矩阵；U为控制向量；X(k)为交通流航空器数量向量；Y(k)为相邻SEL输入航空器数量向量。

1.5 MM2D模型约束条件

X(k+1)可简化为X(k)、可控输入U(k)和扰动输入W(k)的线性组合，即

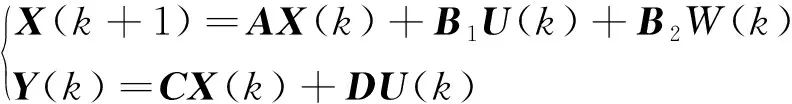
(7)

一系列控制U(k)达到控制目标为

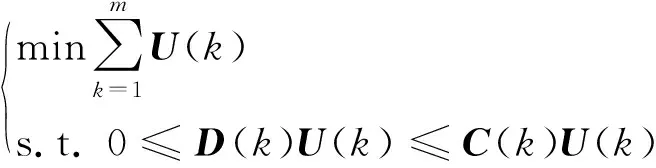
(8)

对于空中交通流系统的控制而言，一个SEL的流出率不能小于0，而且必须小于或等于离开二维面元的航空器的数目,即在保证系统处于稳定状态的前提下，施加流量控制指令应尽可能少。

2 离散时间系统分析

从宏观交通流的角度，空中交通网络及其中流动的交通流可视为离散时间的空中交通流系统，管制员对空中交通网络中航空器的等待指令可视为对系统施加的控制。在现代的空中交通流量管理中，为保证空中交通流系统安全稳定的高效运行，需要对流量进行控制和规划管理，因此本文建立基于MM2D模型的终端区交通流控制系统，结合离散时间系统理论对交通流进行控制分析。

2.1 能控性分析

如果在有限的时间周期内，控制系统能够从任意初始状态转移至某个期望的状态(也是任意状态)，则此系统称为状态完全可控的，即在有限时间期间每个状态变量都可被某个无约束的控制信号控制时，那么系统为可控的。如果存在独立于控制信号的状态变量，则控制该状态变量是不可能的，于是系统是不可控的。

设离散系统的状态方程为

X(k+1)T=GX(kT)+HU(kT)

(9)

假设当kT≤t<(kT+1)T时，U(kT)为常值。其中，X(kT)为n维向量，U(kT)为r维向量，G为n×n矩阵，H为n×r矩阵，那么该系统状态完全可控的充要条件是n×nr矩阵[H∶GH∶…∶Gn-1H]的秩为n，即

rank[H∶GH∶…∶Gn-1H]=n

(10)

2.2 李雅普诺夫稳定性分析

对于控制系统，稳定性是需要研究的一个基本问题，其实质是考察系统由初始状态扰动引起的受扰运动能否趋近或返回到原平衡状态。在现代控制理论中，李雅普诺夫第二方法是研究稳定性的主要方法，既是研究控制系统理论问题的一种基本工具，又是分析具体控制系统稳定性的一种常用方法。

对于给定线性定常离散系统x(k+1)=Ax(k)。其中x(k)∈Rn，A为n×r常数矩阵。设λ1,λ2,…,λn为矩阵A的n个特征值(可以相同)，记|λi|为特征值λi的模或绝对值。则有：

该系统渐近稳定的充分必要条件为

|λi|<1，i=1,2,…,n

(11)

该系统稳定的充分必要条件是：

|λi|≤1，i=1,2,…,n

(12)

式(12)中：当|λi|=1时，λi为A的最小多项式的单根。如果存在某个特征值λi，使得|λi|>1，或者|λi|=1，但λi为A的最小多项式的重根，则该系统不稳定。

3 利用MM2D方法建立空域交通流模型

作为中国最繁忙的空域之一，西安空域是东北-西南和西北-东南方向航路的汇聚点，从地理位置上来看，有得天独厚的航空运输优势，特别是北京大兴国际机场和成都天府国际机场投入运行后更是成为连接西南空域和华北空域的重要纽带。其中，作为进场航班脱离航路执行进近着陆和离场航班起飞后加入航路的过渡区、飞行程序之间相互渗透和制约，终端区空域是整个空中交通网络中最复杂的空域。西安终端管制区高度范围为6 000 m(含)至咸阳塔台管制区外围边界高度，属于C类空域，西安终端区水平区域图和进离场程序，如图4所示。近年来，西安终端区空中交通流量快速增长，空域资源日趋紧张，以西安进近管制空域为背景，同时考虑05L跑道对应的6条标准进场程序和4条标准离场程序建立终端区交通流MM2D模型。

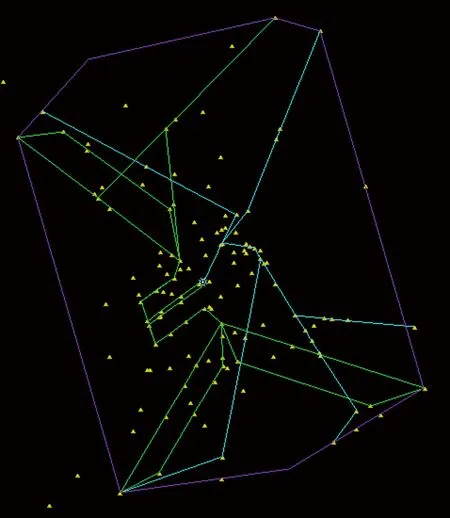
图4 西安终端区空域情况Fig.4 Airspace situation of Xi’an terminal area

3.1 西安进近管制空域交通流建模

由于空域栅格化需要对选定航空管制区中的每个SEL进行建模。因此，SEL的尺寸不能过大，以提供合理分辨率，避免过大的计算误差；也不能过小，以满足航空器间安全运行间隔，同时便于建模分析。根据《中华人民共和国航空资料汇编》中扇区边界数据，西安进近管制空域南侧NSH(宁陕)与北侧NUGLA(洛州)相距289 km；东侧SHX(商县)与西侧HO(长武)相距 255 km。在考虑实际航路走向、航段距离以及SEL个数等因素后，本文确定SEL尺寸为：边长35 km，对角线长度50 km，并依此对西安进近管制空域进行栅格化处理。

本文中使用TAAM软件对栅格化空域进行仿真建模，首先根据西安区域管制空域及相关空域机场信息、航路航线信息、导航台配置情况等，选取西安区域管制空域某典型繁忙日全天运行的1 337条领航计划报数据，使用TAAM软件中Cloning Tool功能，建立连续五日的时刻表，构建静态模型。其次，模型经一线管制员根据所涉及空域相关的管制思路对模型进行动态修正，构建动态模型，较大程度地模拟目标空域的运行过程，目标空域栅格化仿真模型如图5(a)所示。

由于实际的航段长度与走向并不能完全契合SEL交通流的预定走向，为更好地表征以及分析空域系统，将西安咸阳国际机场对应的标准进离场飞行程序结构视为一种星型拓扑结构进行简化处理，作为进场交通流的终点和离场交通流的起点SEL(4,5)位于机场上方，空域结构复杂同时承载大量的交通压力，因此视为该结构的中央节点，其余各SEL的命名及简化后的建模结果如图5(b)所示。其中，各SEL计量符号上的带箭头短线段表示管制员发布的流量控制所应用的方向，即每个方向线段代表在每个SEL上的状态方程中的一个差分方程。

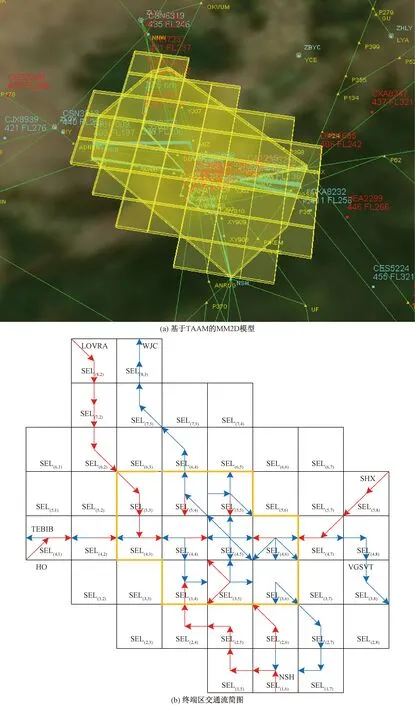
图5 西安终端区空域交通网络简图Fig.5 Schematic diagram of airspace traffic network in Xi’an terminal area

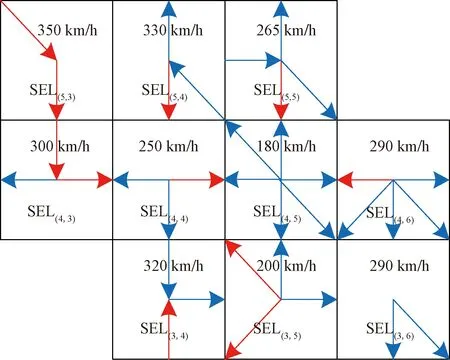
图6 改进终端区MM2D模型Fig.6 Improved MM2D model of terminal area

传统的MM2D模型将交通流视为恒速流处理，但是对于进离场航空器而言，程序起止间的速度相差往往在200 km/h以上，恒速的处理会导致模型失真。因此，根据TAAM中航空器实际运行数据，确定各SEL中的平均速度。这种空间离散化使得采样步长为3 min(0.05 h为一个时间单位)，MM2D模型的精度依赖于交通流率的变化和空域离散化程度(即元胞的物理尺寸)，与航空器数量无关。元胞尺寸由交通流平均速度和理想的时间分辨率决定。根据Shanon采样定理，时间分辨率通常为交通流模式变化率的2倍以上[12]。因为对于一个特定形式的交通流，要满足采样定理，即一个信号中采样频率应该至少是两倍的最高频。交通流数据预期在6 min或更长时间上发生重大变化，则通过控制体的时间必须在3 min或更少的时间内，即采样时间为3 min。MM2D模型包含29个SEL，因为西安进近管制空域存在ZL(R)306、ZL(R)307、ZL(R)308和ZL(R)309四个限制区，部分栅格并无交通流存在，同时移交点附近的交通流方向变化较少、航段复杂度较低，因此剔除此类栅格，仅对SEL(4,5)等10个SEL及其产生的35条交通流进行分析。

3.2 空域状态方程的建立

因为空中交通流系统模型中每个SEL的划分约为一个时间步长所能确定的尺寸，所以在每个SEL中，流量分离参数以及没有飞出SEL的航空器占航空器总数的比率a(i,j,m)在单个时间步长中假定是不变的。本文中仅对位于西安机场上空且空域结构最为复杂的中央节点SEL(4,5)内空域状态方程进行分析。

对于SEL(4,5)方向1的交通流为

(13)

对于SEL(4,5)方向3的交通流为

(14)

对于SEL(4,5)方向5的交通流为

(15)

对于SEL(4,5)方向7的交通流为

(16)

对于SEL(4,5)方向8的交通流为

(17)

对于SEL(4,5)方向9的交通流即到场交通流为

(18)

对于SEL(4,5)方向10的交通流即离场交通流为

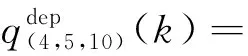
(19)

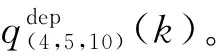
3.3 模型数据的选取

本文中时间间隔设置为0.05 h。为使得方程简化，取T=1，即一个时间单位。aj=1-vjtj/Ωj，Ωj为交通流的物理尺寸，控制体中如果没有管制行为，则航空器将会在下一个时间步长飞入随后的一个控制体，所以大部分SEL的a(i,j,m)均取值为0。参照实际情况对参数进行计算，代入各个二维面元SEL可得，以SEL(4,5)为例演示参数计算过程如下。

因为其中方向1对应的航路距离约为10 km，SEL平均速度为180 km/h，步长为9 km，故没有飞出SEL的比例为a(4,5,1)=(10-9)/9=0.1，同理可得a(4,5,3)=0.1、a(4,5,7)=0.357、a(4,5,8)=0.55、β(4,5,1,10)=0.070、β(4,5,3,5)=1、β(4,5,4,3)=1、β(4,5,7,10)=0.442、β(4,5,8,10)=0.550。

鉴于大多数交通流驻留比率为0，现仅列举非零的交通流驻留比率以及流量分离参数的取值结果，具体见表1和表2。

3.4 系统能控性及稳定性结果分析

根据离散时间控制系统的相关理论，空中交通流系统能控性可由矩阵A和矩阵B确定，通过计算矩阵的秩，rank[BABA2B…A34B]=35，系统满秩，证明该系统完全可控。通过计算矩阵A的特征值为：0.04、0.194、0.517和0.529，均小于1，证明空域系统是渐近稳定的。

对于目标空域，能控性分析可以用来确定其能否由其中控制变量U的组合来进行控制，即根据能控性的概念可得出用来管制飞机数目在期望的限制中的最小组合。这一点也是符合现实的，因为就本文中考虑的建模空域而言，实际工作中，不可能各SEL二维面元的8个方向上都存在管制调控。

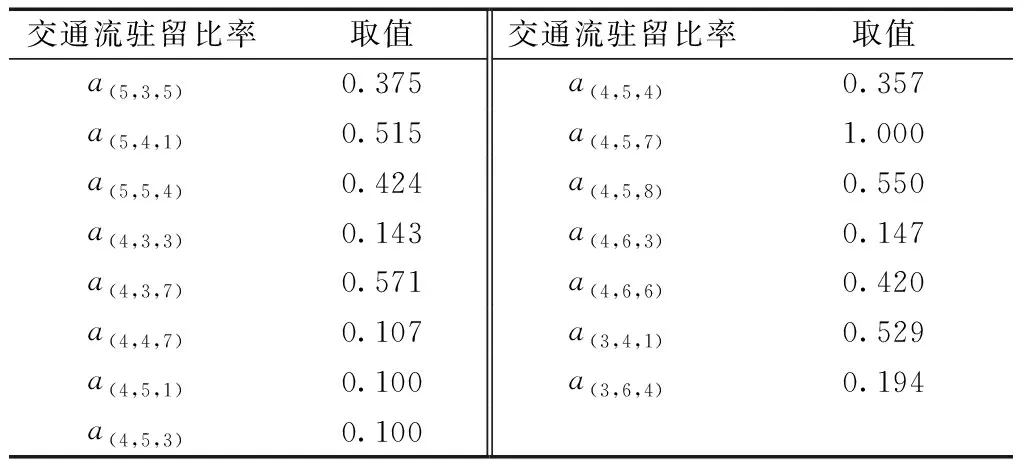
表1 交通流驻留比取值

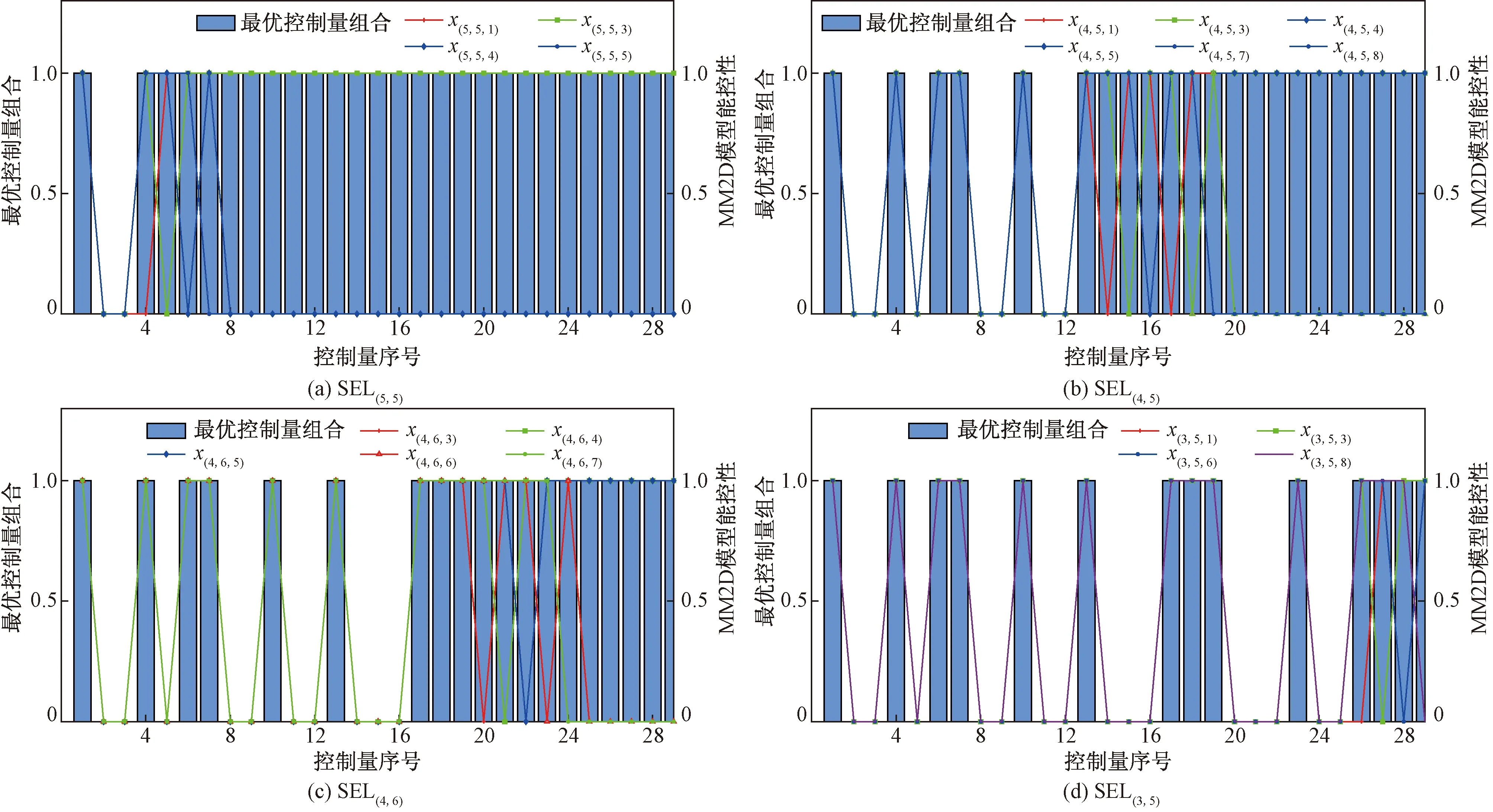
图7 最优控制量组合及稳定性分析Fig.7 Optimal control quantity combination and stability analysis

表2 流量分离参数取值

在空域容量逼近极限的情况下，空中交通流的流动可视为对有限的空域资源和管制员生理和心理资源的竞争。因此管制资源的配置要根据现实出发，从资源的配置的角度考虑，交通流的控制应在完全能控性的前提下最大限度减少管控量，避免管制负荷的增加和管制效能的下降。根据式(8)，系统的能控性可根据能控性矩阵的秩的判断，通过对每个SEL中交通流的可缩减情况进行遍历分析，得出该空域模型达到完全能控下的最小控制量U的组合，部分SEL的空中交通流控制情况如图7所示。

图7中，系统的能控性用1代表能控，0代表不能控。以SEL(3,5)中x(3,5,3)为例，绿线的走向表示，当管制员放弃对此交通流的控制，系统能控性矩阵不满秩，说明在拥挤发生时空中交通流系统将处于失稳状态；紫线的走向表示，当管制员放弃此交通流的控制，系统能控性矩阵满秩，此时该系统依然处于完全能控状态，实际管制过程中可缩减对该方向交通流的控制。最终，在既满足现实因素即每个SEL中至少有一个控制量又达到完全能控的前提下，对35条交通流中的19条施加控制即可实现空域系统的完全能控，交通流控制率可缩减45.7%，得到最优控制组合为：在SEL(5,4)、SEL(3,4)、SEL(3,5)和SEL(3,6)中，最少有1个控制量的存在；在SEL(3,4)、SEL(4,3)和SEL(4,6)中，最少有2个控制量的存在；在SEL(4,5)和 SEL(5,5)中，最少有3个控制量的存在，才能保证MM2D系统完全能控。