流固耦合作用下富水深埋隧道帷幕注浆力学模型

吴松锋， 刘忠， 李奇， 胡丰产

(1.河南省核技术应用中心， 郑州 450044； 2.黄河水利委员会黄河水利科学研究院， 郑州 450003)

随着中国交通网的不断发展与完善，公路、铁路建设已逐步向西南部地区延伸[1-2]。中国西南地区地下水资源丰富，山脉众多且地势起伏较大，而隧道是公路、铁路穿山的重要手段之一，在交通网建设中将不可避免地出现越来越多的富水深埋隧道[3]。随着埋深的增加，隧道初始地应力会达到相当高的水平；在高地应力的作用下，隧道突水、涌泥灾害频发，严重威胁施工安全。

帷幕注浆法采用布孔注浆的形式在隧道围岩表面形成一道堵水帷幕，可以对隧道突水、涌泥实现有效控制[4-6]。帷幕注浆法具有堵水效果好、施工周期短等优点，在工程界得到了广泛的应用：张庆松等[7]对灰岩角砾岩隧道破碎围岩带的涌水灾害进行了分析，通过改善注浆帷幕法的工艺和注浆材料使隧道涌水得到了成功控制。莫阳春[8]、王遇国[9]、Shi等[10]、张成平等[11]对帷幕注浆法在岩溶隧道中的堵水效果进行了工程验证。祝俊等[12]通过修正帷幕注浆参数使强风化花岗岩隧道的突水突泥灾害得到有效控制。宋瑞霞等[13]基于现场帷幕注浆试验以及室内试验的结果，对帷幕注浆法在黄土隧道中的围岩含水量控制以及围岩变形控制效果进行了研究。李嘉璐等[14]采用数值模拟与现场监测相结合的方法，获得了未注浆、超前半断面注浆以及全断面注浆情况下隧道支护应力及变形间的关系，验证了帷幕注浆法的可靠性。王聪等[15]通过数值模拟手段分析了不同注浆范围对围岩稳定性和渗流规律的影响，并给出了隧道超前帷幕注浆的合理范围。学者们也对帷幕注浆法开展了理论方面的相关研究：任文峰[16]基于裂隙岩体渗流模型，获得了帷幕注浆法注浆圈参数与隧道涌水量之间的定量关系。Zhang等[17]采用正交分析方法，研究了注浆厚度和渗透性对隧道涌水量和围岩稳定性的影响。王凯[18]考虑浆液在围岩中的扩散过程，采用弹性力学中的Flamant解答推导了帷幕注浆厚度的控制方程。尚宏波等[19]推导了浆液与地下水两相流的控制方程，并通过有限元软件分析了帷幕注浆法在不同工况下的浆液扩散规律。周晓敏等[20]建立帷幕注浆后的围岩渗流场与应力场解析式，并分析了注浆参数对岩体渗流场和应力场的影响规律。

目前针对帷幕注浆法的工程应用已经积累了大量研究成果，证实了帷幕注浆法在工程中的可靠性，而对于帷幕注浆法的理论研究较少且尚未形成系统。帷幕注浆除对地下水具有封堵作用外，还对围岩具有一定的加固作用，这种加固作用会改善围岩的变形场与应力场，考虑这种加固作用可以减少围岩支护成本，而学者们在推导理论模型的过程中对这种流固耦合作用的考虑并不全面，致使采用理论模型计算得出的隧道应力、变形等均过于保守。

基于此，考虑注浆后注浆帷幕刚度的增大与渗透系数的减小作用，建立隧道帷幕注浆力学模型，推导了帷幕注浆后隧道围岩位移和有效应力的计算方程；以大瑞铁路某富水深埋隧道为工程依托，采用Abaqus有限元软件验证力学模型的合理性与可靠性。研究成果可为相似工程帷幕注浆法的设计与施工提供理论支持。

1 考虑流固耦合作用的隧道注浆帷幕力学模型

1.1 基本假设

为简化推导过程，将帷幕注浆后的隧道断面视为稳态平面模型，如图1所示，且满足以下假设：

(1)当隧道完成帷幕注浆后，同一区域内的围岩视为各向同性，且围岩处于弹性平衡状态。

(2)隧道断面等效为厚壁圆筒模型，忽略喷射混凝土的抗渗作用。

(3)隧道围岩所处的地下水环境径流补给充足，浅水下的渗流状态视为承压含水状态。

(4)考虑到围岩刚度较大的特点，仅考虑渗流场对围岩应力场的单向耦合作用；且渗流场服从达西渗流定律，流固耦合作用服从广义太沙基理论。

为加固体内缘孔隙水压力；为外边界孔隙水压力；a为隧道半径；ur为径向位移；σθ为环向总应力；σr为径向总应力；σA为注浆加固区内的径向应力；ps为径向的结构应力；为隧道内充满水时，作用在加固体内缘上的孔隙水压力，对于无水交通隧道，为原岩区内的径向应力；r为径向坐标值；rc为加固区 与原岩区交界面径向坐标值图1 隧道平面模型示意图Fig.1 Schematic diagram of the tunnel plane model

1.2 力学模型建立

为使力学模型可以考虑无穷远处的原岩区域，对隧道径向距离作如下变换，即

(1)

式(1)中：a为隧道半径；r为径向距离；ρ为转换系数，当ρ→0时，径向距离趋于无穷远，当ρ=1时，径向距离即为隧道半径。

取注浆加固区内的一微元体进行分析，根据达西定律[21]可计算微元体处的流量q，计算公式为

(2)

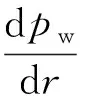
(3)

根据连续性假设，流量Q需在半径为r的任意圆周截面上相等，即满足边界条件

(4)

联立式(3)和式(4)，获得平衡方程，即

(5)

联立式(1)和式(5)，得

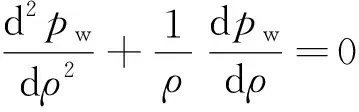
(6)

对式(6)进行积分，得

pw(ρ)=C1+C2lnρ

(7)

式(7)中：C1、C2为积分常数。

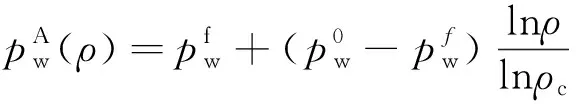
(8)

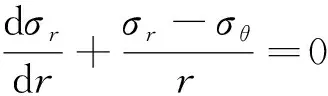
(9)

联立式(1)与式(9)，得

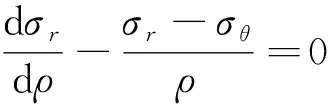
(10)

基于经典弹性理论，应力增量与应变增量之间呈线性关系；根据太沙基有效应力原理，此时只有有效应力才会使围岩产生变形。因此，存在关系

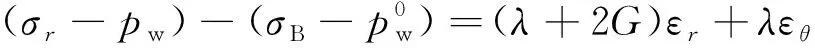
(11)

(12)

联立式(11)和式(12)，并考虑式(10)的平衡条件，得

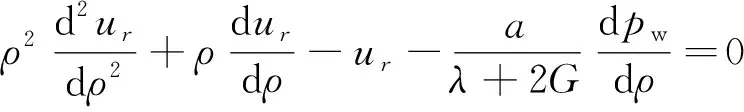
(13)

对式(13)进行积分，得注浆加固区内的围岩位移表达式为

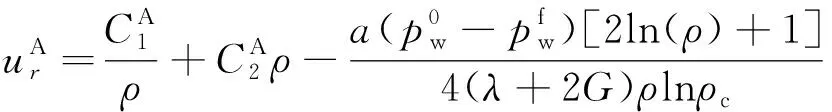
(14)

联立式(13)和式(14)，求得注浆加固区内的有效径向应力和有效环向应力为

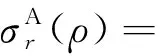
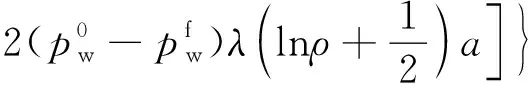
(15)

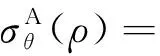
(16)

式中：W与水力梯度成正比。

对于原岩区，假设孔隙压力与位置无关，此时，应满足平衡方程

(17)

对式(17)进行积分，可得原岩区的位移表达式为

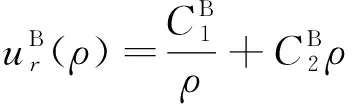
(18)

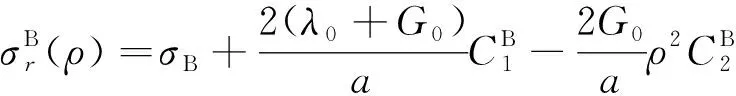
(19)

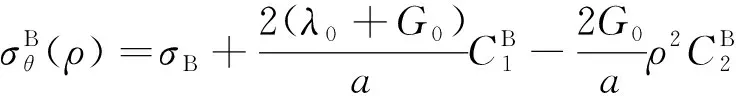
(20)

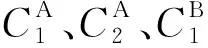
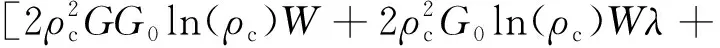
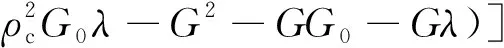
(21)

将边界条件代入相应的积分方程内，即可求得

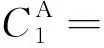
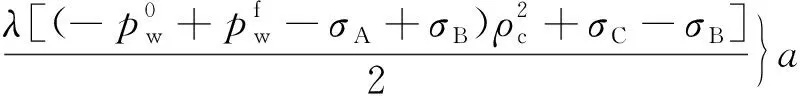
(22)

至此，流固耦合作用下隧道帷幕注浆力学模型建立完毕，可由该模型计算帷幕注浆后隧道围岩的有效应力场和位移场。

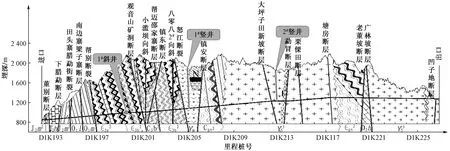
图2 地质剖面图Fig.2 Geological profile

2 算例验证

为确定所建立的隧道帷幕注浆力学模型的合理性与可靠性，以大瑞铁路某富水深埋隧道为工程依托，制定6种注浆堵水方案，推导了6种方案的解析表达式，并采用数值模拟方法进行验证。

2.1 工程概况

某富水深埋隧道为大瑞铁路的控制性工程，隧道全长34.5 km，隧址区属高黎贡山余脉，山岭呈南北走向，东北地势高，西南地势低，地形起伏大，地面高程最高达2 340 m，隧道最大埋深1 155 m，属超深埋隧道。隧道共穿越19条活动断裂带，隧址区岩性复杂，软岩段以千枚岩、板岩为主，硬岩段以灰岩、花岗岩为主(图2)。由于受孟加拉湾暖温气流的影响，年平均降雨量最高可达2 597.7 mm，最大日降雨量可达100.8 mm，地下水丰富，施工过程中涌水量大且较难控制。

2.2 力学模型解析解

研究位置选取隧道正洞DK219+567断面，如图3所示，该断面埋深700 m，围岩等级为V级，岩体极为破碎，属强富水区。采用TBM(tunnel boring machine)掘进施工，施工过程中涌水量过大，采用帷幕注浆法进行加固。由于在相同水压边界条件下，影响注浆圈应力场、位移场分布的主要因素为剪切模量和弹性系数，因此改变剪切模量和弹性系数的大小，制定6种注浆加固方案，方案1～3改变剪切模量比，G/G0分别为1、1.5和2；方案4～6改变弹性系数比，分别为0.15、0.20和0.25。其他参数按施工资料与现场监测结果进行取值，各方案计算参数选取如表1所示。

将表1中的参数代入式(21)和式(22)中，求得参数结果如表2所示。

则方案1～6的解析解分别为

(23)

表1 依托工程计算参数选取

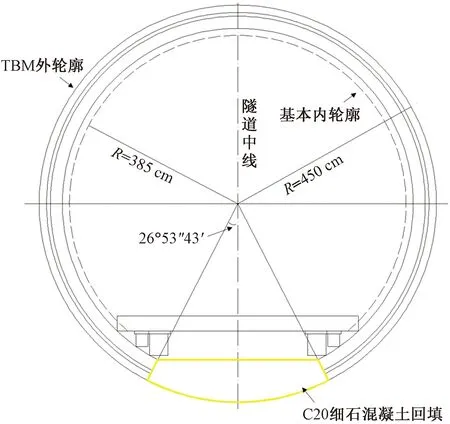
图3 隧道断面图Fig.3 Tunnel section

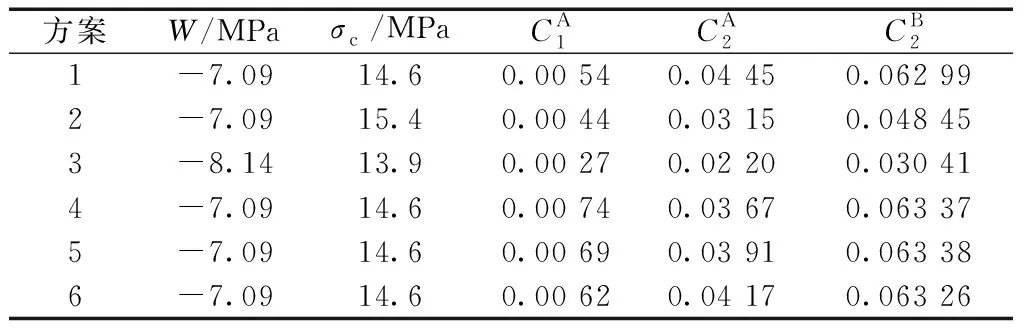
表2 参数计算结果

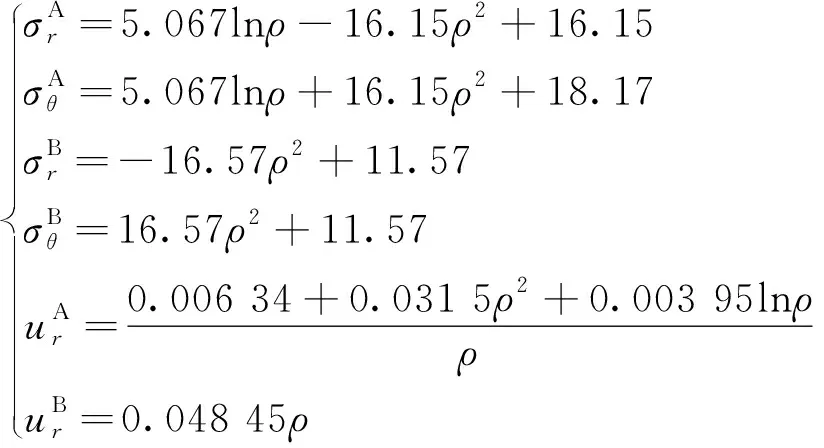
(24)

(25)

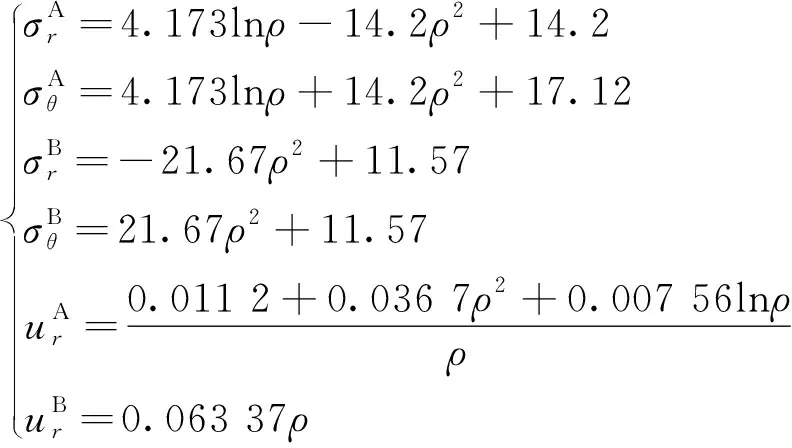
(26)

(27)

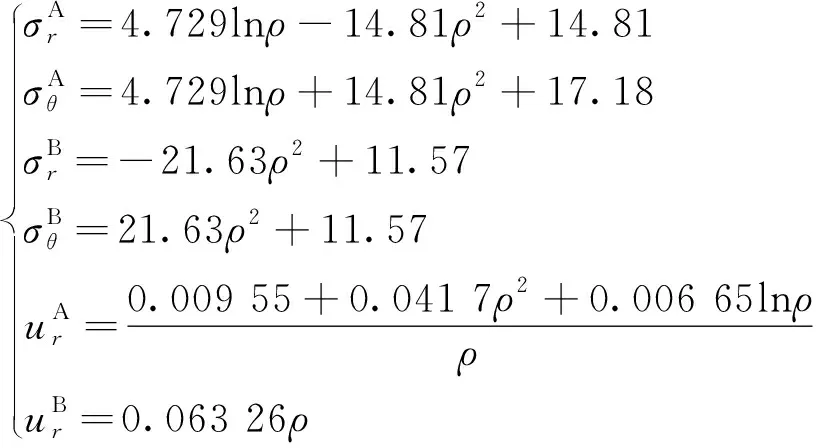
(28)

分别绘制6种方案下的位移、环向应力和径向应力曲线，如图4～图6所示。由图4可知，当距离中心点越近时，围岩的位移越大，位移最大点均出现在距中心点4.5 m处，即围岩内壁处；当注浆加固后的围岩剪切模量越小时，围岩的位移越大，G/G0=1时，围岩最大位移为82.86 mm；当注浆加固后的围岩弹性系数越小时，围岩的位移也越大，λ/λ0=0.15，围岩最大位移为51.22 mm。由图5可知，当距离中心点越近时，围岩的环向应力越大；随着剪切模量和弹性系数的增大，围岩的环向应力在增大，G/G0=2时，在距中心点4.5 m处环向应力达到最大，最大值为34.32 MPa，λ/λ0=0.25时，环向应力的最大值为31.99 MPa。由图6可知，围岩的径向应力变化规律与位移和环向应力变化规律相反，当距离中心点越远时，径向应力越大；随着剪切模量和弹性系数的增加，围岩的径向应力也在增大，最大径向应力分别为8.60 MPa和7.79 MPa。

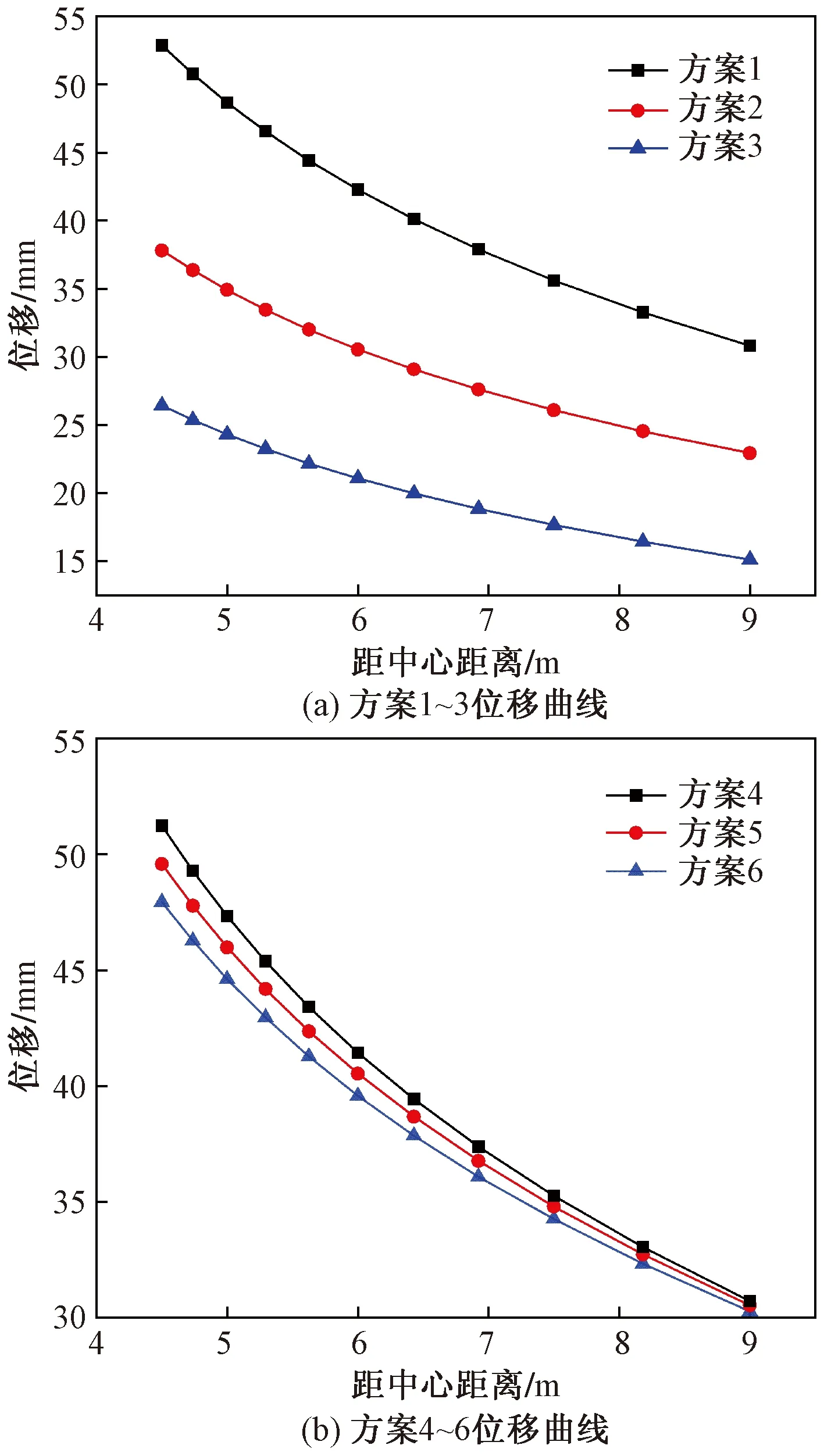
图4 不同方案位移解析解曲线Fig.4 Analytical solution curve for displacement of different schemes

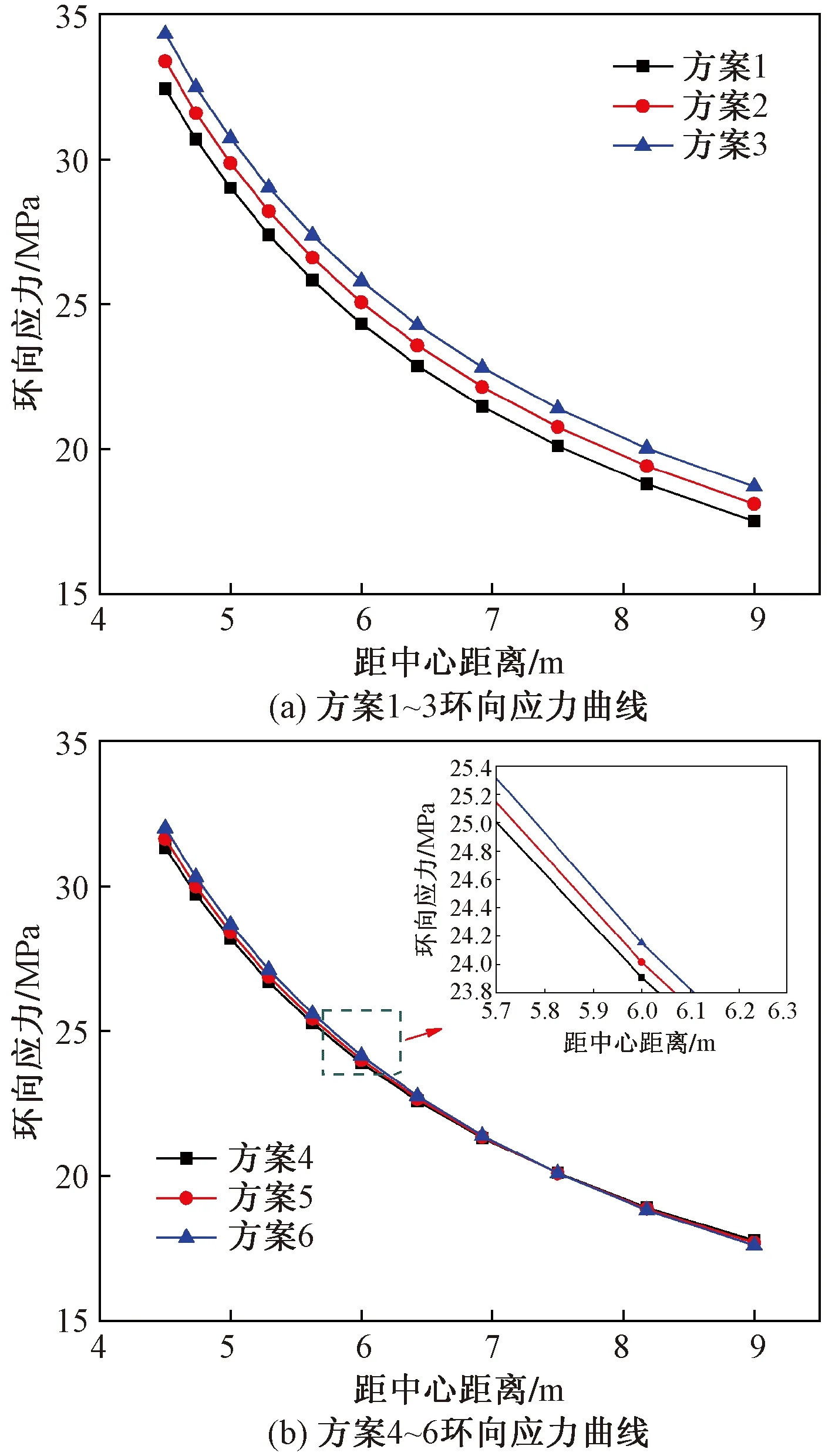
图5 不同方案环向应力解析解曲线Fig.5 Analytical solution curve of hoop stress for different schemes

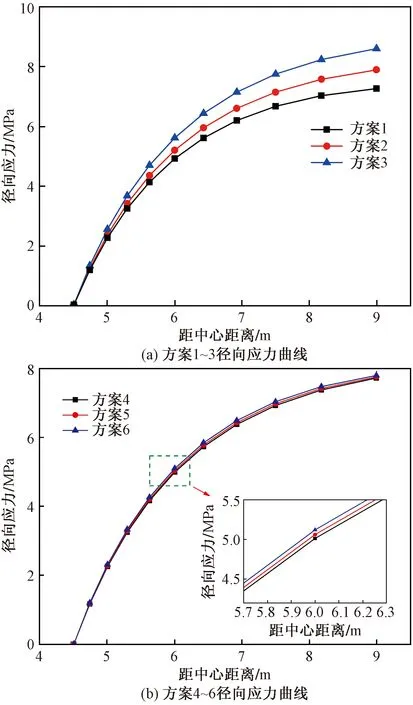
图6 不同方案径向应力解析解曲线Fig.6 Analytical solution curve of radial stress for different schemes

综上所述，距离组隧道中心点越远时，围岩的位移与环向应力会越小，径向应力会越大。增大围岩的剪切模量和弹性系数，有助于减小围岩的位移，但会增大围岩的径向与环向应力。

2.3 数值模拟验证

为验证模型计算结果的准确性，采用Abaqus有限元软件对方案2进行数值模拟验证，模型参数按表1进行取值，数值计算模型如图7所示。为了使数值计算模型满足力学模型假设，模型外边界取 1 000 m，注浆圈半径取11.25 m，隧洞半径取 4.5 m，外边界为总应力边界。注浆帷幕外边界水压与模型外边界水压值相同，注浆帷幕内边界(隧洞洞壁)水压值为0，本构关系采用线弹性模型。

图8和图9给出了数值模拟的位移与应力计算对比结果。

图7 数值计算模型Fig.7 Numerical calculation model

图8 数值模拟位移结果对比Fig.8 Comparison of numerical simulation displacement results

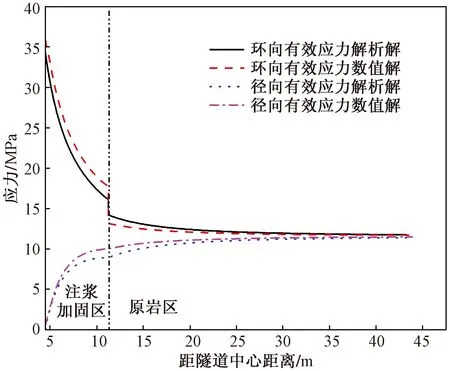
图9 数值模拟应力结果对比Fig.9 Comparison of numerical simulation stress results

由图8可知，由隧道注浆帷幕力学模型计算的围岩位移值与数值模拟的位移计算结果非常接近，平均误差为5.02%，最大误差出现在距隧道中心11.25 m处，误差为9.35%。由图9可知，由隧道帷幕注浆力学模型计算的围岩应力值与数值模拟的应力计算结果也非常接近。注浆加固区内的环向应力平均误差为4.73%，最大误差为6.20%，径向应力平均误差为4.26%，最大误差为6.03%。

整体而言，由隧道帷幕注浆力学模型计算的隧道围岩位移值与应力值结果与数值模拟计算结果规律相近，且误差均在10%以内，证明了本文推导的帷幕注浆力学模型的合理性与可靠性。

3 现场监测

大瑞铁路某富水深埋隧道在DK219+567段面采用方案2对开挖面进行了帷幕注浆处理，隧道涌水量得到显著控制，此后对DK219+567断面进行了应力与位移监测，应力监测采用YH-45型压力盒，位移监测采用IM-100型全站仪，如图10所示。

D1K219+567断面采用TBM掘进施工，开挖跨度9.0 m，为便于分析，应力与位移的监测结果均取最大值与解析解和数值解进行对比，解析解和数值解取距中心距离4.5 m处的结果，对比结果如表3所示。

图10 监控量测设备Fig.10 Monitoring measurement equipments

表3 监测结果对比

由表3可知，所选断面应力与位移的现场监测结果最大值分别为32.5 MPa和35.60 mm，解析解和数值解与监测结果相比均非常接近，应力解析解与监测结果的误差为10.2%，位移解析解与监测结果的误差为6.2%，这也证明本文所提出的隧道帷幕注浆力学模型具有较好的工程适用性，计算结果相对可靠。同时，现场的应力与位移监测结果均满足规范要求，也表明本文提出的注浆方案2可以保证大瑞铁路某富水深埋隧道开挖施工的堵水效果与施工安全。

4 结论

基于流固耦合理论，考虑注浆对围岩的加固作用，建立了隧道帷幕注浆力学模型，并以大瑞铁路某富水深埋隧道为工程背景，采用理论计算、数值模拟与现场监测相结合的方法验证了模型的准确性，获得以下结论。

(1)基于流固耦合理论，在厚壁圆筒模型的基础上推导了隧道注浆帷幕力学模型，该模型可计算隧道帷幕注浆加固后的围岩位移和有效应力。

(2)分析了围岩剪切模量和弹性系数对注浆加固后围岩位移场和应力场的影响。结果发现，增大围岩的剪切模量和弹性系数，有助于减小围岩的位移，但会增大围岩的径向与环向应力。

(3)采用Abaqus有限元软件对模型进行了验证，结果表明，围岩位移场与应力场的计算结果与数值模拟结果规律相近，且误差均在10%以内；模型计算结果与现场监测结果的最大误差仅为10.2%，证明了该模型合理可靠。

(4)现场的应力和位移监测结果满足规范要求，表明本文提出的帷幕注浆加固方案可以保证隧道施工安全。