涡轮叶片裂纹故障的3维叶尖间隙变化特性分析

2022-02-06熊逸伟张小栋刘洪成黄鑫徐志豪朱家浩

航空发动机 2022年6期

熊逸伟，张小栋，2，刘洪成，黄鑫，徐志豪，朱家浩

（1.西安交通大学机械工程学院，2.现代设计及转子轴承系统教育部重点实验室：西安 710049）

0 引言

涡轮叶尖间隙是航空发动机的关键状态参数之一，叶尖间隙的变化不仅对航空发动机涡轮的工作效率、油耗以及使用寿命具有较大的影响[1]，而且反映了涡轮叶片的故障信息。因此，对涡轮叶尖间隙的实时在线监测能够为航空发动机涡轮叶片的故障诊断奠定良好的基础。为了得到具有针对性的故障特征，更好地实现涡轮叶片故障诊断，对涡轮叶尖间隙变化机理的研究至关重要。

国内外学者对涡轮叶尖间隙的变化机理展开了研究。Lattime等[2]认为发动机载荷和飞行载荷是影响高压涡轮叶尖间隙的主要因素；Kypuros等[3]和Agarwal等[4]建立了涡轮叶片、轮盘和机匣的简化数学模型，进而得到叶尖间隙动态变化的简化模型；岂兴明等[5]和句彦松[6]采用有限元方法对涡轮叶片、轮盘和机匣的径向变形量进行数值计算，得到发动机各工况下涡轮叶尖径向间隙的变化规律；贾丙辉等[7-8]研究了飞机机动飞行以及转子裂纹故障对高压涡轮叶尖间隙变化规律的影响。上述对于涡轮叶尖间隙变化机理的研究，都仅考虑了径向间隙。然而，在复杂的载荷条件下，涡轮叶片会在3维空间内发生变形，导致叶尖间隙具有空间3维特征。滕飞等[9-10]提出了涡轮3维叶尖间隙，并利用有限元方法研究了不同长度和位置的叶片裂纹故障对3维叶尖间隙的影响特性；熊逸伟等[11-12]研究了热疲劳载荷以及航空发动机加速过程对涡轮3维叶尖间隙的影响特性。涡轮3维叶尖间隙除径向间隙外，还包括轴向偏转角和周向滑移角[9]，反映了涡轮叶片沿转子轴向和周向的弯曲变形，而气动载荷是造成叶片弯曲变形的主要因素。于贵齐[13]建立了涡轮叶片气动载荷沿转子轴向和周向的计算模型；Bai等[14]利用深度学习算法对涡轮叶片表面的气动载荷分布进行了预测；Choi等[15]利用数值计算方法研究了转静子轴向间隙对高压涡轮叶片气动性能的影响。

3维叶尖间隙的变化特性对于涡轮叶片故障诊断的研究至关重要。由于涡轮的实际工作环境非常恶劣，通常采用有限元方法研究3维叶尖间隙的变化特性。在影响叶尖间隙的多种因素中，气动载荷导致的涡轮叶片弯曲变形会对轴向偏转角和周向滑移角产生影响；尾缘裂纹是涡轮叶片的典型故障，其故障信息会反映到3维叶尖间隙的变化上。因此，在通过有限元方法分析3维叶尖间隙的变化特性时，气动载荷及裂纹故障的影响非常重要。本文研究了涡轮叶片3维叶尖间隙的有限元分析模型，进而对比分析了涡轮叶片有无裂纹情况下3维叶尖间隙变化特性的差异。

1 涡轮转子3维叶尖间隙有限元分析模型

1.1 涡轮转子有限元分析模型

航空发动机涡轮转子的真实结构非常复杂，为了便于加工制造，对用于试验台上的涡轮模拟转子的结构进行了简化。模拟转子由轮毂和叶片组成，叶片高50 mm，通过螺栓固定到轮毂上，轮毂半径为20 mm，因此涡轮转子的半径为70 mm。尽管模拟转子叶片与轮毂之间的螺栓连接与航空发动机涡轮叶片与轮盘之间常用的榫头连接有所不同，但在2种连接方式下均可将涡轮叶片视为悬臂梁模型，涡轮叶片在载荷下的变形也不会受到连接方式的影响。因此，上述简化不会对数值模拟结果的正确性产生显著影响。此外，为了更真实地模拟涡轮叶片，叶身有一定的扭转角度。并且，叶尖表面设计为与机匣内表面同轴的圆柱面，以保证在静止状态下叶尖表面各点处的3维叶尖间隙在转子的圆周方向具有一致性，涡轮模拟转子几何模型如图1所示。

图1 涡轮模拟转子几何模型

由于涡轮转子转速较高，单个叶片经过机匣参考点的时间非常短。在试验台上模拟涡轮转子的典型工作转速为3000 r/min，转子叶片从靠近到离开参考点的整个过程中转动的角度为15°，则转动的时间仅为1/1200 s，因此，该过程可视为瞬态过程。为了分析瞬态过程中模拟转子涡轮叶片3维叶尖间隙的动态变化特性，采用显式动力学方法进行仿真计算。对涡轮模拟转子的几何模型进行网格划分，得到涡轮模拟转子有限元分析模型，如图2所示。

图2 涡轮模拟转子有限元分析模型

在进行有限元分析时，对涡轮模拟转子有限元分析模型进行了适当简化。由于涡轮转子沿圆周方向具有循环对称的结构特点，因此取模拟转子的1/6扇区进行分析，以减少有限元分析的计算量。另外，模拟涡轮转子的叶片和轮毂采用螺栓连接，但在仿真计算中没有建立螺栓的有限元模型。尽管叶片与轮毂的连接处存在相对振动，但由于有限元仿真的时间仅1/1200 s，在如此短的时间内，振动对叶尖间隙变化特性的影响较小。因此，在有限元仿真中不考虑叶片与轮毂连接处的振动对3维叶尖间隙变化特性的影响，而采用“绑定”的方式连接叶片和轮毂，保证其相对位置不变。此外，为了对比有无裂纹故障叶片的3维叶尖间隙变化特性的差异，在叶片尾缘处设置了不同长度的裂纹。由于不同材料的力学性能具有一定的差异，叶片材料的选择会对有无裂纹故障叶片3维叶尖间隙仿真结果的数值大小产生影响。航空发动机涡轮叶片材料通常为镍基高温合金，较小的载荷难以使其变形。为此，选择铝合金作为模拟转子叶片的材料，保证叶片在试验台的载荷条件下具有相对明显的变形。为了确保计算的精度，对裂纹尖端附近区域的网格进行了细化。并且，为了保证显示动力学分析的收敛性，设置自动时间步长，并设置最大循环次数为1×107次，保证每个子步具有足够小的时间步长。

1.2 气动载荷数学模型

在涡轮运行过程中，叶片会受到转子高速旋转造成的离心载荷作用，以及燃烧室高温高压燃气造成的热载荷和气动载荷作用。离心载荷和热载荷会导致涡轮叶片和轮盘的径向变形，进而影响叶尖径向间隙。然而，高温高压燃气流经导向叶片后，会直接冲刷涡轮转子叶片，导致叶片弯曲变形，进而对于轴向偏转角和周向滑移角产生显著的影响。因此，对于涡轮叶片3维叶尖间隙的变化特性，需要重点考虑气动载荷的影响。为此，在针对模拟转子的仿真研究中，为了研究气动载荷对3维叶尖间隙的影响，首先需要对气动载荷进行模拟。于贵齐[13]利用傅里叶级数展开建立了涡轮叶片气动载荷的数学模型，涡轮叶片轴向气动载荷pa和周向的气动载荷pu分别表示为

式中：n为傅里叶展开的级数；N为静子叶片数；Ω为转子转速；t为时间；a0a和a0u分别为轴向和周向气动载荷傅里叶展开式中的常数项；ana,bna和anu,bnu分别为轴向气动载荷和周向气动载荷傅里叶展开式中的各项系数。

根据式（1），假设n=6，且模拟转子转动15°的过程中经过1个静子叶片，即N=1。结合理想气体状态方程以及试验台上用于施加气动载荷的高压风机的工作参数，分别计算轴向气动载荷和周向气动载荷，将其按照矢量进行合成，并将合成后的气动载荷施加到模拟转子叶片的表面。最终，施加到叶片表面的气动载荷如图3所示。

图3 叶片表面的气动载荷

1.3 叶片尾缘裂纹参数

涡轮叶片在复杂的载荷条件下极易发生故障，尾缘裂纹则是涡轮叶片的典型故障之一。裂纹的出现使叶片在复杂载荷作用下的变形进一步加剧，进而对涡轮3维叶尖间隙产生影响。由于涡轮叶片尾缘厚度较薄，强度较低，因此在叶片尾缘更容易发生裂纹故障，并且气动载荷容易导致叶根附近区域出现应力集中现象。为此，将裂纹设置在叶片尾缘处距离叶根5 mm的位置。此外，对于涡轮叶片裂纹故障诊断，裂纹扩展到一定程度叶片可能断裂，因此需要尽早发现叶片上的微小裂纹故障。考虑到涡轮模拟转子的叶片宽度为18 mm，为此，在叶片尾缘处分别设置长度为2、4、6 mm的裂纹（如图4所示），表示不同严重程度的裂纹故障，进而分析在不同长度的裂纹故障下涡轮叶片3维叶尖间隙的变化特性。

图4 不同长度的叶片尾缘裂纹

1.4 3维叶尖间隙数值求解方法

为了分析涡轮叶片3维叶尖间隙的动态变化特性，需要定义1组参考点来计算3维叶尖间隙。在以往研究中，参考点通常选择为叶尖表面上的固定点[9-11]。但实际上，3维叶尖间隙反映的是叶尖表面与机匣内表面之间的空间特征，且叶片与机匣的相对位置会发生变化。因此，可在机匣上选择固定的参考点，提取参考点与叶尖表面之间的径向距离来计算3维叶尖间隙。为此，在有限元分析过程中，在叶尖表面上方的机匣上定义1个切平面作为参考平面，并在切平面上定义3个固定不动的直角坐标系，将参考点定义在直角坐标系的原点处。当叶片位于参考点下方时，提取参考点到叶尖表面的径向距离来计算出3维叶尖间隙。根据文献[16]提出的3维叶尖间隙光纤测量传感器的探头结构，3个参考点呈等腰直角三角形排布，如图5所示。3个参考点沿水平方向和竖直方向的距离d=2 mm，并且参考点0位于叶尖表面的几何中心的正上方。

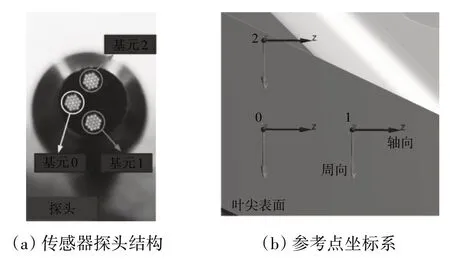
图5 传感器探头结构及参考点坐标系选择

假设在ti（i=1，2，…，m，m为有限元分析输出的时间步数）时刻，3个参考点同时位于叶尖表面上方，且各参考点到变形后的叶尖表面的径向距离分别为x0(ti)、x1(ti)和x2(ti)，则ti时刻的径向间隙h(ti)、轴向偏转角α(ti)和周向滑移角β(ti)分别为

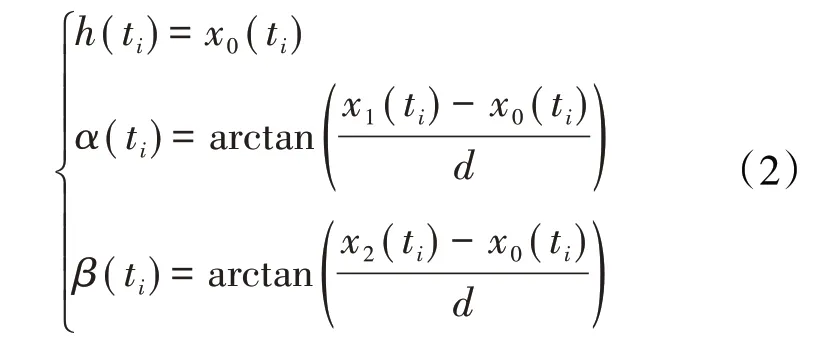
按照式（2）计算出不同时刻下的3维叶尖间隙值就可以得到涡轮叶片3维叶尖间隙的变化特性。需要注意的是，只有当1组参考点的3个坐标系同时位于叶尖表面上方时才能够计算3维叶尖间隙。

2 无裂纹涡轮叶片的3维叶尖间隙变化特性分析

为了保证涡轮叶尖表面各处的叶尖间隙在圆周方向具有一致性，在机匣内表面为圆柱面的假设条件下，叶尖表面也应该为圆柱面，如图6所示。因此，在不施加任何载荷、不考虑转子振动的理想条件下，模拟涡轮转子的3维叶尖间隙应为定值。对于径向间隙，叶尖表面和机匣内表面的半径分别为70、73 mm，因此在理想条件下径向间隙为3 mm。从涡轮转子周向视角来看，叶尖表面的顶端为直线，参考点位于机匣切平面内，因此在理想条件下轴向偏转角为0°；从涡轮转子轴向视角来看，叶尖表面为圆弧，假设参考点0位于该圆弧顶点的正上方，参考点2与参考点0均在机匣的切平面上，且间隔距离为2 mm，则参考点0和2到叶尖表面的径向投影距离不相等。此时可以计算出2个参考点在叶尖表面投影点的连线与机匣切平面的夹角约为0.82°，此为理想条件下的周向偏转角。

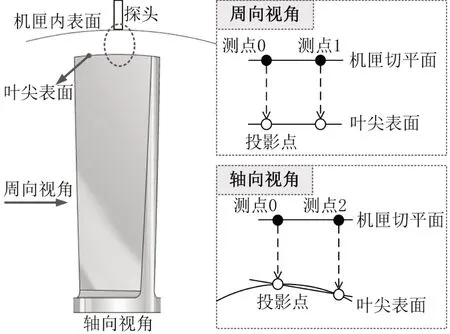
图6 模拟转子叶尖表面

涡轮叶片在气动载荷作用下发生弯曲变形，因此3维叶尖间隙也随之改变。对于上述模拟涡轮转子，在气动载荷作用下，涡轮叶片经过参考点时其3维叶尖间隙的动态变化如图7所示。

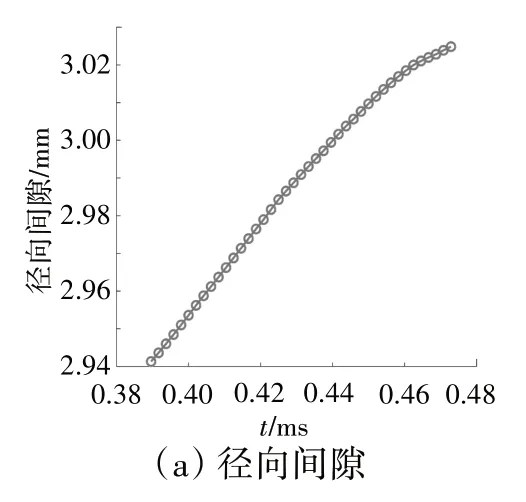
图7 无裂纹叶片的3维叶尖间隙

从图中可见，在无裂纹叶片经过参考点的过程中，径向间隙逐渐增大，周向偏转角逐渐减小，而轴向偏转角呈先略微增大然后减小的趋势。在气动载荷作用下，叶片沿轴向和周向发生变形，变形后的叶尖表面不再是与机匣内表面同轴的圆柱面，因此3维叶尖间隙也不再是定值。从图7（a）中可见，叶片经过参考点时，径向间隙的变化幅度约为0.09 mm，因此气动载荷对径向间隙的影响相对较小。为了得到轴向偏转角和周向滑移角，需选择3个参考点同时位于叶尖表面的时刻进行计算。根据图5（b）中参考点和叶尖表面的相对位置关系可知，当叶片转动离开参考点2时，便无法计算3维叶尖间隙，而此时叶片几乎位于3个参考点的正下方。因此，根据如图5（b）所示参考点得到的3维叶尖间隙变化特性反映了叶片逐渐靠近参考点的过程，此时轴向偏转角和轴向滑移角均呈现逐渐减小的变化趋势。因此，在气动载荷作用下，当无裂纹叶片经过参考点时其3维叶尖间隙不再是理论上的定值，并且气动载荷对轴向偏转角和周向滑移角的影响比对径向间隙的影响更为显著。

3 裂纹故障涡轮叶片的3维叶尖间隙变化特性分析

为了对比分析不同严重程度的裂纹故障叶片相对于无裂纹叶片其3维叶尖间隙变化曲线特征，在涡轮叶片尾缘的相同位置定义了不同长度的裂纹，裂纹特征参数如图8所示。

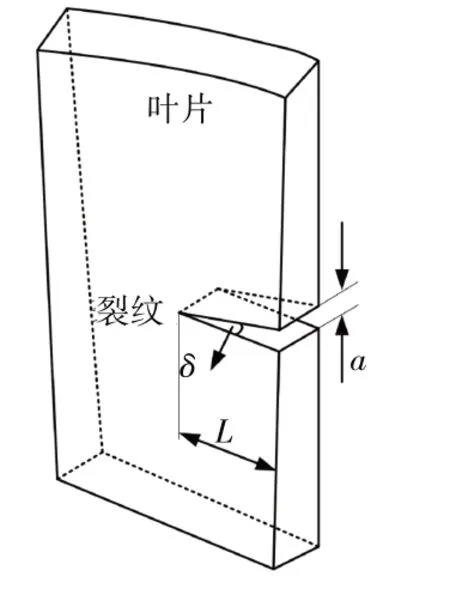
图8 裂纹特征参数

在有限元分析过程中，裂纹长度L=2、4、6 mm，表示涡轮叶片不同严重程度的裂纹故障。在改变L时，裂纹开口高度a保持不变。因此，L越短，其裂尖张开角δ越大。在气动载荷作用下，当叶片经过参考点时，不同叶片的3维叶尖间隙变化特性如图9所示。

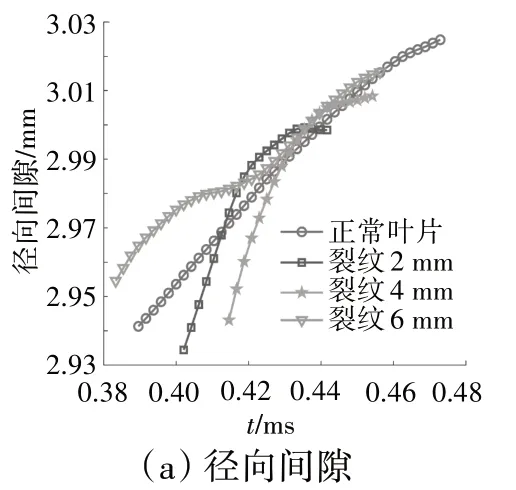
图9 裂纹叶片的3维叶尖间隙

在气动载荷作用下，裂纹叶片3维叶尖间隙变化特性变得更加复杂。从图中可见，有无裂纹叶片的径向间隙均呈现逐渐增大的变化趋势，并且数值上差异不大。由于径向间隙主要受离心载荷的影响，因此在相同转速条件下，有无裂纹叶片的径向间隙具有一致的变化趋势。裂纹故障会导致径向间隙的数值差异，但差异不明显。然而，有无裂纹叶片的叶片轴向偏转角和周向滑移角的变化特性差异明显。对于裂纹故障叶片，气动载荷引起的弯曲变形会导致裂纹面被挤压，裂尖张开角δ减小，从而导致轴向偏转角和周向滑移角增大；然而离心载荷会导致裂纹面被拉开，δ增大，从而导致轴向偏转角和周向滑移角减小，并且裂纹长度越大，离心载荷对裂纹的拉伸作用越强。综合考虑气动载荷和离心载荷的影响，裂纹长度为6 mm的叶片受离心载荷的影响更显著，导致其轴向偏转和和周向偏转角小于无裂纹叶片的。

从图9（b）、（c）中可见，在裂纹长度为2、4 mm时，受气动载荷的影响更为显著，裂纹面在气动载荷作用下被迅速挤压，裂纹叶片的轴向偏转角和周向滑移角也迅速减小，从而导致叶片的轴向偏转角和周向滑移角变化曲线斜率更大。有无裂纹叶片的轴向偏转角和周向滑移角变化曲线斜率有明显差异，可作为叶片裂纹的一种故障特征，用于涡轮叶片裂纹的故障诊断。

从图9（b）中还可见，裂纹长度为6 mm的叶片的轴向偏转角在第0.41 ms处突然增大，然后再逐渐减小。并且，在第0.42 ms之后，其轴向偏转角减小的速率与其它裂纹叶片的相当。裂纹长度为6 mm的叶片经过参考点的时间段约为第0.38～0.46 ms。由图4可知，在第0.38～0.41 ms的气动载荷最大，之后逐渐减小。因此，当气动载荷较大时，裂纹面被挤压；随着气动载荷逐渐减小，被挤压的裂纹面逐渐分离，在此过程中，叶片的刚度可能发生突变，因而导致轴向偏转角突然变化。当裂纹面分离之后，裂纹长度为6 mm的叶片的轴向偏转角减小速率与其它裂纹叶片的一致。由于正常叶片轴向偏转角的变化曲线较为平滑，轴向偏转角的突变可作为一种故障特征用于识别涡轮叶片是否存在裂纹故障。