粗糙表面接触刚度模型的研究进展
2022-02-06艾延廷解松霖刘玉田晶赵丹刘俊男
艾延廷,解松霖,刘玉,田晶,赵丹,刘俊男
(1.沈阳航空航天大学航空发动机学院,2.辽宁省航空推进系统先进测试技术重点实验室:沈阳 100136;3.中国航发四川燃气涡轮研究院,成都 610550)
0 引言
相互接触的零件之间的结合部分被称为“机械结合面”,航空发动机机匣安装边螺栓连接结构便是装配形成的机械结合面。机械结合面之间的接触并非光滑的面与面之间的接触,而是由许多微凸体之间的相互接触构成的[1],导致2个粗糙表面接触时的实际接触面积总是小于名义接触面积[2-3]。在航空发动机中这种结合面分布广泛,结合面间的接触刚度对航空发动机整机结构的稳定性、可靠性有着至关重要的影响[4-5],准确计算结合面间的接触刚度在航空发动机设计中尤为关键[6-7]。为了准确计算粗糙表面间的接触刚度,需要对粗糙表面间的微凸体接触进行建模。粗糙面接触模型主要分为解析模型和有限元模型。目前大部分粗糙表面接触模型都属于解析模型,表征粗糙面形貌的解析方法主要分为统计描述和分形描述。大部分接触刚度模型主要根据统计学理论接触模型[8-9]及分形理论的接触模型[10-11]建立。
关于粗糙表面间接触建模已有许多研究成果[12-13]。Bhushan[14]于1996年将粗糙表面上的单个微凸体间相互接触的问题分为弹性解析模型和弹塑性有限元模型来分类叙述;贺林等[15]于同年对粗糙面接触分形模型进行了概述;Bhushan[16]于1998年将之前建立的粗糙表面接触模型按照微凸体的轮廓形状和分布高度分为2类进行了讨论;Adams等[17]在2000年将微凸体间的接触分为单个微凸体的接触和多个微凸体的接触,特别介绍了接触面之间作用力(即粘着力)的产生;魏龙等[18]于2009年对粗糙表面接触模型的发展进行了总结,分别介绍了Hertz接触模型、统计学接触模型和分形接触模型的优劣性;Ghaednia等[19]于2017年分别按照微凸体的几何形状和加载方式对单个微凸体接触模型进行了评述。
随着航空发动机技术的发展,发动机结构设计变得尤为关键。机匣做为发动机主要承力部件,需要具有足够的刚度来保证发动机稳定运行。由螺栓连接所构成的机匣安装边作为机匣中最重要的一环,可有效地提升其接触刚度,对整个发动机结构稳定性有着至关重要的影响。接触模型的发展目前已较为完善,但是关于接触刚度模型的综述性文章仍然非常匮乏。
本文对国内外不同的粗糙面接触刚度模型的发展历史和研究现状进行了总结,重点对接触刚度的计算进行了详细阐述。分析了现有结合面接触刚度模型的不足,展望了接触刚度模型的发展趋势。
1 粗糙表面的描述和表征
1.1 单个微凸体接触
要建立完整的粗糙表面接触模型,首先要清楚粗糙表面上的单个微凸体受载荷的变形规律,该问题被称为赫兹接触[20-22],是微观接触力学中的一个重要问题,被众多学者所关注和研究。研究发现,粗糙表面上的单个微凸体在变形过程中共经历3个阶段:相互接触的微凸体首先进入弹性变形阶段,随着载荷的增加逐渐进入弹塑性变形阶段,当载荷达到一定值时进入塑性变形阶段。
当微凸体处于弹性变形阶段时,由赫兹接触理论可知,接触面积ae、接触载荷fe、最大接触压力pem、平均接触压力pea分别为
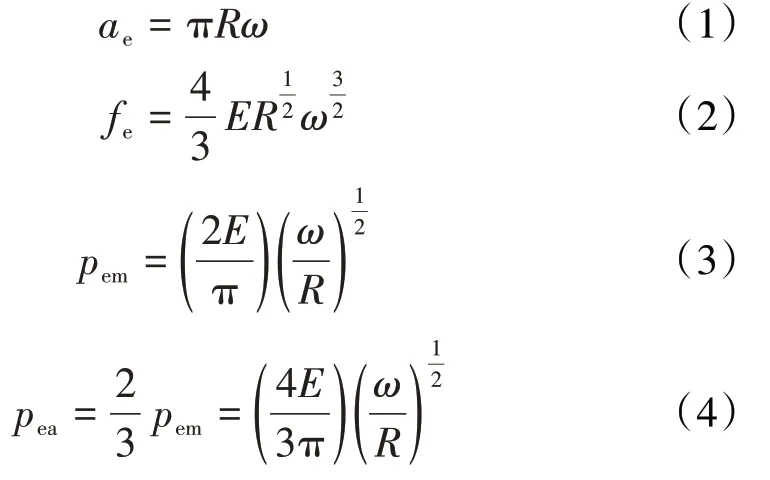
式中:R为相对曲率(R=1/R1+1/R2);R1、R2分别为2个微凸体的半径;E为等效弹性模量,1/E=(1-υ12)/E1+(1-υ2
2)/E2,E1、E2和υ1、υ2分别为2个微凸体的弹性模量和泊松比;ω为微凸体的变形量。
当微凸体所受载荷大于屈服极限时,塑性变形开始在微凸体内部产生,此时微凸体处于弹性变形和塑性变形共存的阶段,即弹塑性阶段[23-25]。大多数弹塑性接触模型都是采用有限元方法建立简化的球体与光滑的平板的接触模型进行分析[26-28]。众多学者将弹塑性变形分为3类,即压平模型、压入模型和综合模型[29-31]。目前还没有从弹塑性变形基本理论推导出闭合解[32-33]。
当载荷达到一定值后,塑性变形由原来的只存在于某一区域迅速扩展至整个微凸体,这种状态被称为完全塑性变形阶段[34-35]。通常采用Tabor[36]、Abbott等[37]的试验结果来计算微凸体处于完全塑性变形阶段时的接触面积ap、平均接触压力ppa和接触载荷fp

式中:H=2.84σy为材料的硬度,σy为材料屈服强度。
1.2 粗糙面表面接触
为了准确地分析粗糙表面间接触行为和接触特性,需要建立与真实物体表面形貌相近的接触模型,表面形貌即粗糙表面微凸体的数量、分布高度、曲率半径、轮廓形状和位置等参数[38]。接触模型主要分为解析模型和有限元模型,其中解析模型是众多学者主要研究的方向,解析模型又具体划分为统计描述模型和分形描述模型。
1.2.1 解析模型
(1)统计学描述。应用统计方法描述粗糙表面最大的特点是可以体现其各微凸体高度的随机性[12],描述方法可分为随机过程描述和微凸体高度分布描述。随机过程描述是指微凸体的分布高度到基体的距离是随机的,这一距离可用某一特定的分布函数和自相关函数来描述,由此表征粗糙表面的形貌特征;微凸体高度分布描述则是假设粗糙表面上所有微凸体的高度和曲率满足某种统计学规律,通过特定的统计分布函数来确定形貌特征。由此可见,微凸体高度分布描述是对随机过程描述的一种简化,将包含多尺度信息的粗糙表面简化为单一尺度的粗糙表面。应用统计描述表征粗糙表面的过程较为简单,极大程度缩短了求解过程,有利于进行粗糙表面间的接触建模,但其不能完全表征粗糙表面所有的形貌特征,无法表征一个确定的粗糙表面。
(2)分形描述。随着对粗糙表面研究的不断深入,发现实际物体的粗糙表面的形成是一个非平稳的随机过程[39],粗糙表面上的微凸体的高度分布与采样设备的分辨率相关,将粗糙表面放大后,可以看到在任意尺度下粗糙表面的形貌特征基本不会发生变化,这就是粗糙表面形貌的自相似性及尺度不变性。因此,可采用分形参数(分形维数和特征尺度系数)来描述粗糙表面的形貌特征。分形理论所描述的物体形貌特征不受空间的束缚,更加接近客观物体的真实属性与状态,更加符合客观物体的多样性与复杂性。应用分形描述的方法来建立粗糙表面形貌特征是分形接触模型的基础,先通过仪器提取物体粗糙表面真实形貌数据,再基于分形理论计算得到与物体粗糙表面形貌相近的分形参数,由分形参数确定粗糙表面的形貌特征,进而建立粗糙表面接触模型。
1.2.2 有限元模型
随着计算机水平的不断进步,有限元仿真方法逐渐被用于微观粗糙面建模中[40-42]。有限元模型可以更直观地观察接触面的微凸体分布、应力分布,其结果更加真实。有限元模型虽然弥补了解析模型的一些不足,但是想要完整地描述粗糙面形貌特征,就必须进行非常细致的网格划分,这样会大幅增加计算时间和计算难度。目前有限元方法通常仅适用于微小的接触模型,对于跨尺度的模型仍存在一些挑战。
2 基于统计描述的粗糙面接触刚度模型
2.1 GW模型
关于粗糙表面接触,Greenwood和Williamson[43]在1966年基于赫兹接触理论提出的GW模型是统计接触模型的典型代表,为其后学者研究粗糙表面间的接触问题奠定了理论基础,至今仍被广大学者广泛使用[44]。
GW模型用1个粗糙面和1个光滑刚性平面等效替代2个相互接触的粗糙表面,其表面上所有微凸体间互不影响,并将所有微凸体等效成具有相同的曲率半径的球形微凸体,微凸体顶点高度分布满足高斯分布,GW模型只针对弹性变形进行了分析,并提出了塑形指数作为弹性、塑形接触状态的区分条件。微凸体与光滑平面的接触如图1所示。图中z为某个微凸体与微凸体平均高度之间的距离,d为微凸体平均高度与光滑平面之间的距离,h为粗糙表面轮廓线平均高度与光滑平面之间的距离,微凸体的变形量ω=zd。φ(z)dz为满足高斯分布的微凸体高度分布函数。
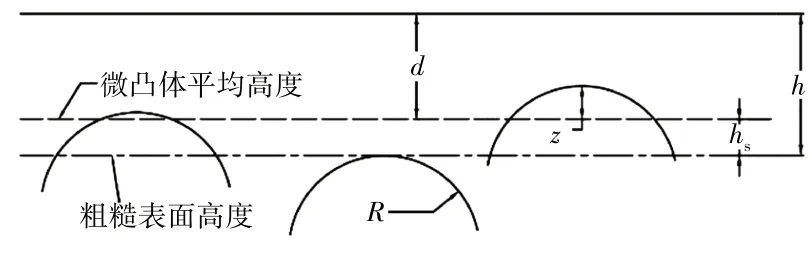
图1 微凸体与光滑平面的接触
根据赫兹接触理论,微凸体总数量为

式中:η为微凸体接触面积密度函数;An为名义接触面积。
当微凸体变形量ω>0,即z>d时,微凸体将与刚性平面发生接触,接触的微凸体总数为
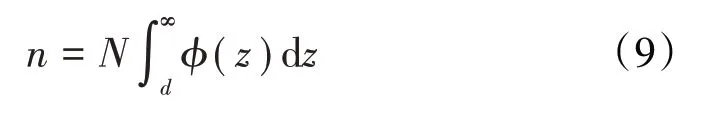
根据赫兹接触理论,总的接触面积A、接触载荷F和接触刚度K分别为
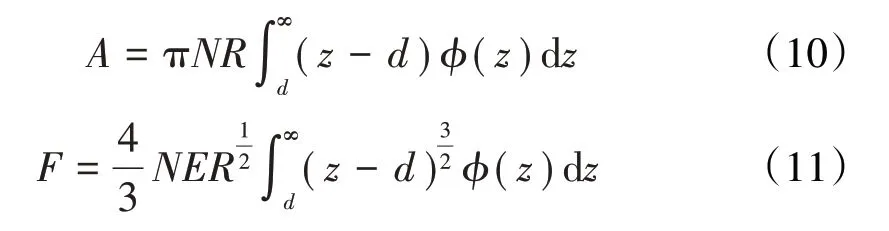
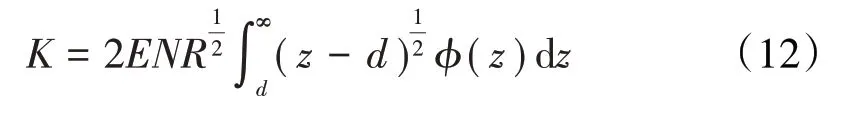
虽然GW模型为其后众多学者广泛借鉴,但仍有许多不足之处:(1)只考虑了微凸体间的弹性作用,忽略了微凸体间的弹塑性及塑性作用;(2)忽略了微凸体间的相互作用,认为各微凸体相互独立、互不影响;(3)将所有微凸体的曲率半径简化为某一恒定的值,这是不符合实际情况的。随着研究的进一步深入,不断有学者对其进行改进和补充。
2.2 考虑弹性及塑性的统计学接触刚度模型
1987年,Chang等[45]在GW模型的基础上建立了CEB模型,将微凸体的变形划分为弹性变形阶段和塑性变形阶段2个阶段,给出了微凸体弹性变形与塑性变形的临界接触变形量ωc,弥补了GW模型只考虑微凸体弹性变形的不足。同时根据单个微凸体在塑性变形过程中体积恒定,给出了单个微凸体处于塑性变形阶段时的接触面积ap、接触载荷fp,计算得到接触刚度kp
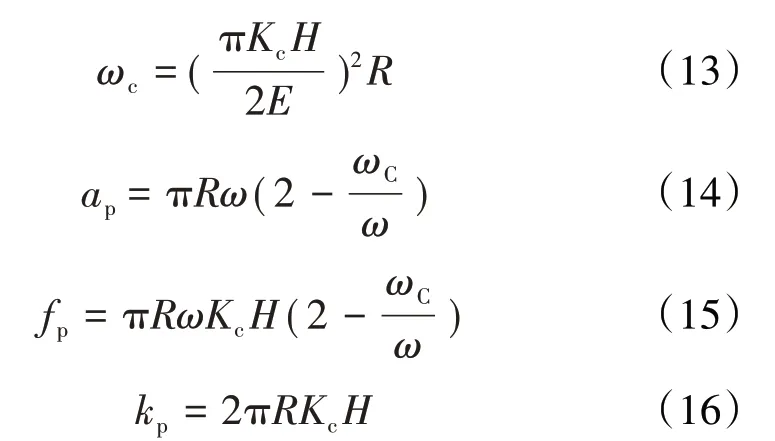
式中:Kc=0.454+0.41μ,为最大接触压力因子,μ为较软材料的泊松比。
随后根据发生接触的微凸体总量,给出了总的接触面积A、总载荷F,计算得到总接触刚度K
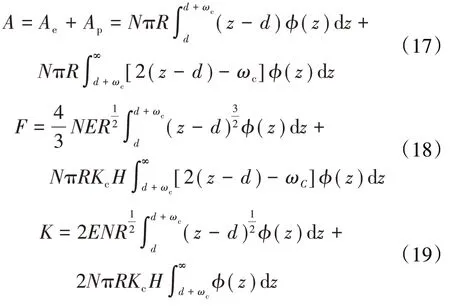
式中:Ae、AP分别为弹性接触面积、塑性接触面积。
CEB模型只考虑了弹性变形及塑性变形,忽略了由弹性过渡到塑性时的弹塑性变形,导致临界点处不连续,接触压力直接从2KH/3突然跳跃至KH。使得接触刚度在由弹性变形向完全塑性变形转化时是不连续的。
2.3 考虑弹性、弹塑性及塑性的统计学接触刚度模型
为弥补CEB模型的不足,2000年,Zhao等[46]基于CEB模型建立了ZMC模型,将微凸体变形划分为弹性阶段、弹塑性阶段、塑性阶段3个阶段。基于4阶多项式和对数函数推导出微凸体处于弹塑性变形阶段时的接触面积、平均接触压力。该方法实现了平均接触压力在弹性屈服点和临界塑性点的连续性,但仍然不具备光滑性,因此该模型建立的接触刚度模型在临界点处是不连续的。
2002年,Kogut和Estion[47]在ZMC模型的基础上采用有限元方法计算了单个球体与刚性平面的接触,并应用幂函数拟合了有限元近似解。基于有限元数据,将微凸体变形分为弹性阶段、第1弹塑性阶段、第2弹塑性阶段、塑性阶段4个阶段。4个阶段临界处对应的微凸体临界变形量分别为ωc、6ωc、110ωc。即当0<ω<ωc时,微凸体处于弹性变形阶段;当ωc<ω<6ωc时,微凸体处于第1弹塑性变形阶段;当6ωc<ω<110ωc时,微凸体处于第2弹塑性变形阶段;当110ωc<ω时,微凸体处于完全塑性阶段。处于弹塑性阶段所对应的接触载荷、接触刚度分别为
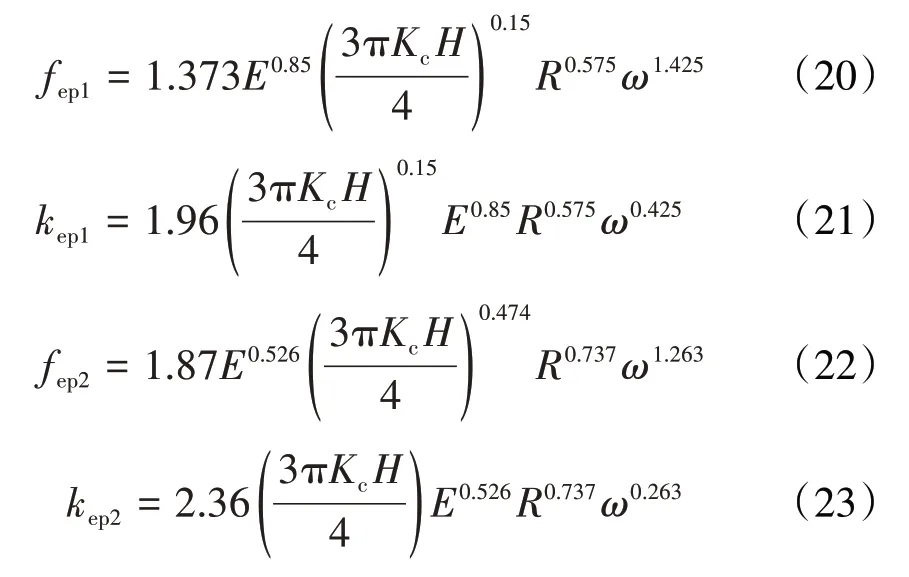
式中:fep1、kep1和fep2、kep2分别为微凸体处于第1、2弹塑性阶段时的接触载荷、接触刚度。
根据GW模型中给出的总的接触载荷、接触刚度思路,可以计算出KE模型总的接触载荷、接触刚度
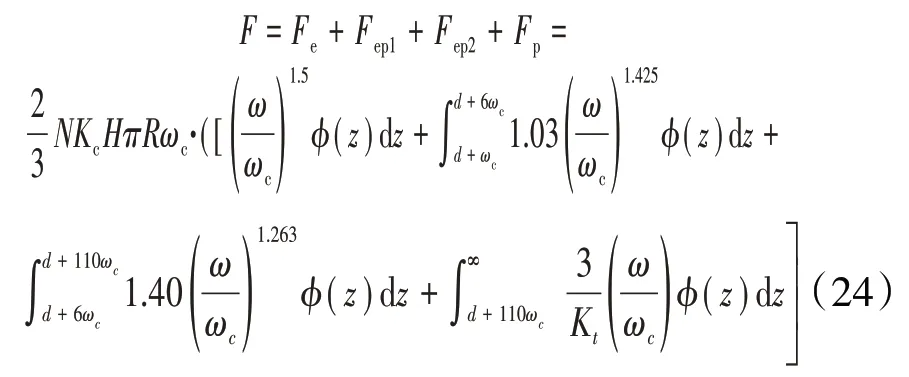
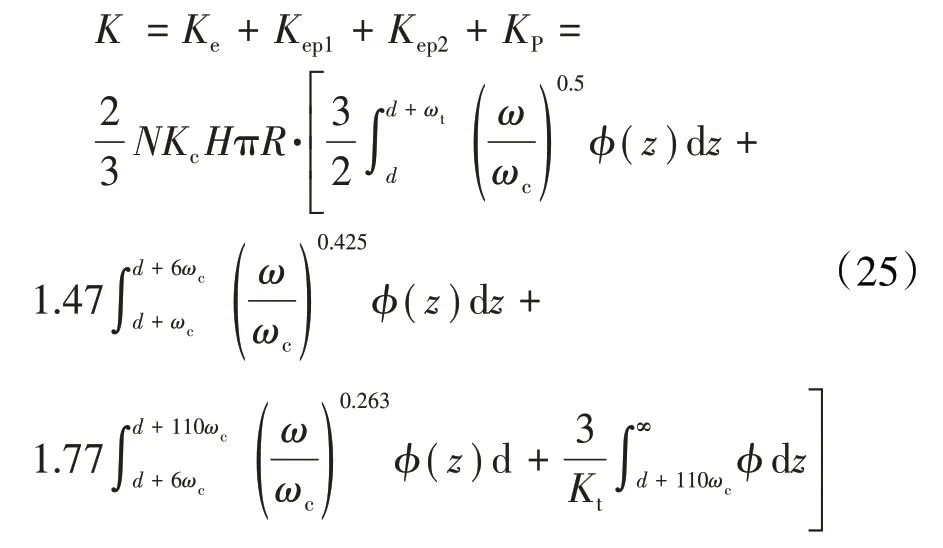
2017年,田小龙等[48]考虑了微凸体间的相互作用,应用勒夫方程和圣维南原理推导出的接触面各参数(接触载荷、局部变形、表面压强)和材料属性之间的函数关系,将其代入微凸体变形量表达式中,得到了更接近真实情况的变形量表达式,将其带入ZMC和KE模型中,得到了考虑微凸体之间相互影响的粗糙面接触刚度模型,ω在弹性阶段的表达式为
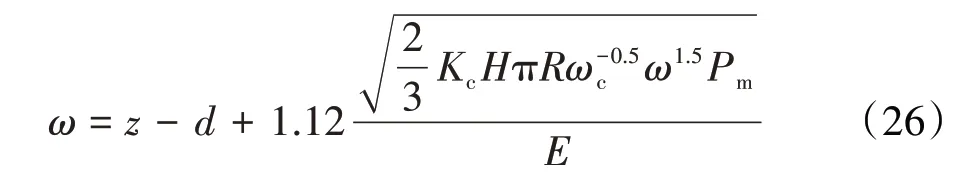
在第1弹塑性阶段的表达式为
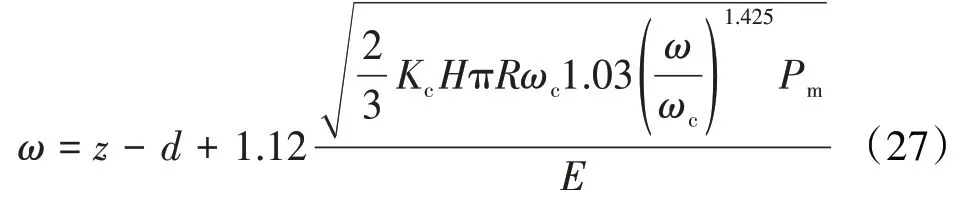
在第2弹塑性阶段的表达式为
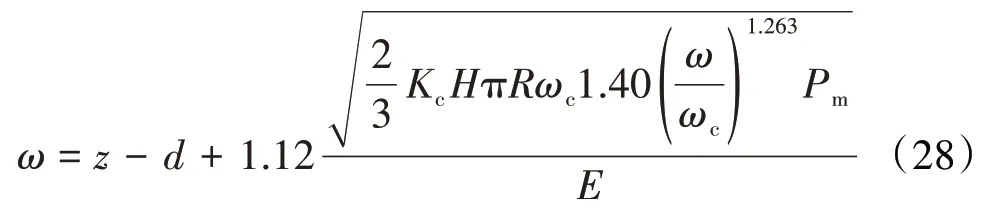
在塑性阶段的表达式为
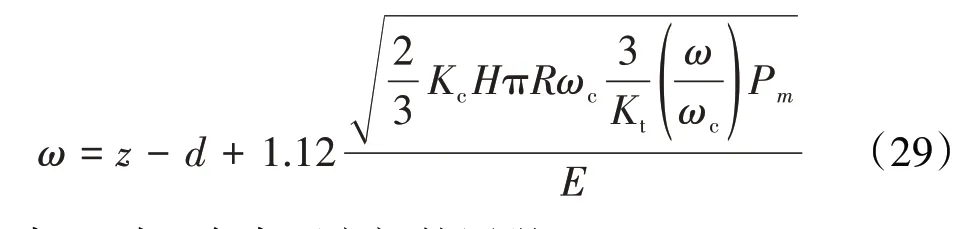
式中:pm为2个表面之间的压强。
Jackson等[23]采用较KE模型有着更精密网格的有限元模型,建立了新的单个微凸体与刚性光滑平面接触的有限元模型,即JG模型,该模型考虑了微凸体变形过程中微凸体硬度变化、几何尺寸变化及材料属性的影响。该模型发现微凸体的弹性变形可在[0,1.9ωc]内发生,在微凸体变形量比较小时,接触载荷、接触面积、接触刚度变化规律与Hertz接触理论基本一致。但JG模型并没有考虑微凸体开始发生塑性变形时的临界接触点。
2.4 具有连续光滑特性的统计学接触刚度模型
2012年,Brake[49]提出了一种微凸体接触载荷为光滑连续的粗糙面模型,应用了Hermit多项式插值函数,但由于Hermit多项式阶次过高,导致弹塑性变形阶段的微凸体接触载荷与变形量的关系出现震荡,从而导致接触刚度数值也出现波动,甚至出现刚度小于0的情况,这是不符合实际情况的。
2021年,李玲等[50]应用Hermit插值方法,使接触载荷在弹性转变为弹塑性临界点及弹塑性转变为塑性临界点处光滑且连续,将接触载荷转换到对数坐标系,减小插值区间,进而降低了由Hermit插值多项式阶次过高带来的震荡。建立了单一微凸体连续光滑的接触刚度模型,然后基于统计学方法进行无量纲处理,得到了结合面接触刚度模型。其单个微凸体弹塑性变形区接触刚度为
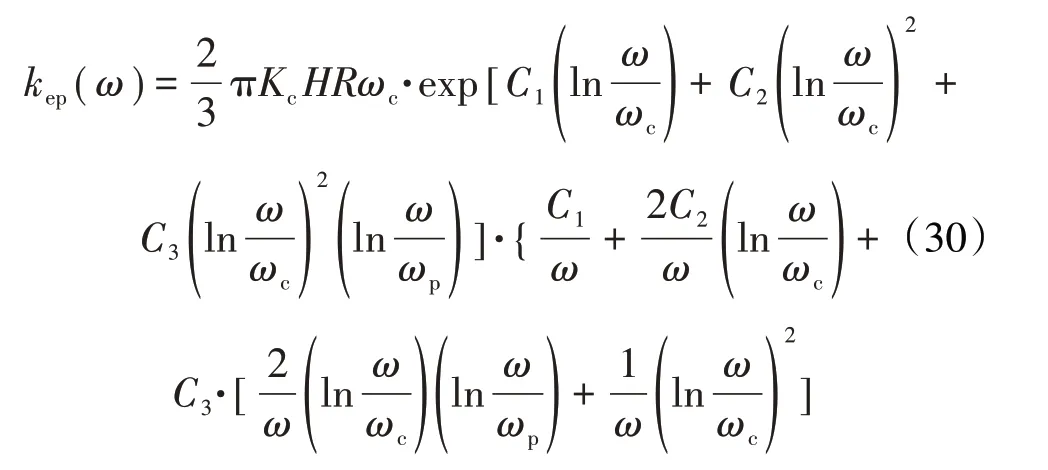
式中:C1、C2、C3为Hermit多项式系数;ωp=110ωc。
基于统计描述所建立的接触模型,有利于描述不同粗糙表面的形貌特征,但由于粗糙表面的不确定性,无法准确地分析粗糙表面的接触特性。在一定测量条件下得到的统计学参数具有局限性,不能表征完整的粗糙表面,这是由于粗糙表面具有多尺度特性所造成的。
为了考虑粗糙表面的多尺度特性,大多数学者采用分形理论来建立接触模型,相较于统计描述更能够反映出粗糙表面的多尺度特性。
3 基于分形描述的粗糙面接触刚度模型
3.1 MB模型
1990年,Majumdar与Bhushan[51]共同提出了基于分形几何理论构建的粗糙表面接触模型,即MB模型,这种模型将实际2个粗糙表面之间的接触简化为1个光滑的刚性理想平面与1个粗糙平面的接触,并且忽略了材料硬度随微凸体深度的变化且假设各微凸体相互独立,不过这一粗糙表面具有分形特性。
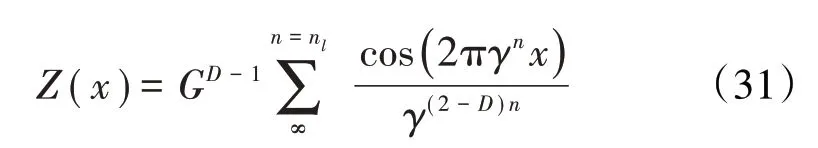
式中:D为分形维数;G为特征尺度系数;x为表面轮廓位置坐标;Z为表面轮廓高度坐标;γn为粗糙表面频率参数。
该模型以W-M分形函数(W-M函数描述的粗糙表面与光滑平面接触如图2所示)及海洋岛屿面积分布规律为基础,研究了单个微凸体变形处于弹性阶段和塑性阶段的变形机制,获得了较为真实的微凸体接触面积与接触载荷之间的关系。给出了微凸体接触面积分布函数n(a)及粗糙表面与刚性平面总的截面积公式,为今后学者的研究奠定了理论基础。
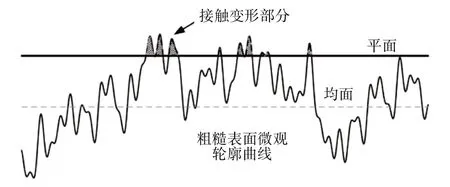
图2 W-M函数描述的粗糙表面与光滑平面接触
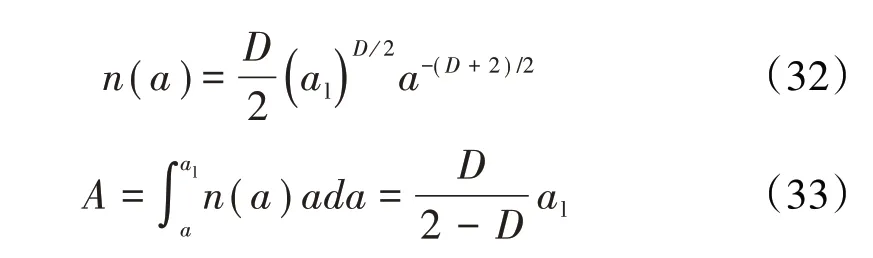
式中:a为粗焅表面单个微凸体接触面积,al为粗糙表面单个微凸体最大接触面积。
Wang等[52]基于MB模型,考虑了温度对微凸体面积分布密度函数的影响,修正了微凸体面积分布密度函数,但忽略了单个微凸体缓慢滑动状态。根据单个微凸体接触面积随温度的变化关系及接触面上的最高温度,修正了MB接触模型,得到了新的弹性、塑性接触模型。
3.2 考虑弹性、塑性的分形接触刚度模型
2000年,张学良等[53-54]基于MB分形模型,假设粗糙表面各向同性,各微凸体间相互独立,考虑了微凸体塑性变形阶段对接触刚度的影响,给出了微凸体由塑性变形变为弹性变形时的临界接触面积ac,
由分形理论可知,当a<ac时微凸体发生塑性形变;当a>ac时微凸体发生弹性形变。这显然与统计学模型相互矛盾。
Morag等[55]针对这一现象给出了解释,当微凸体接触面积非常小时,微凸体会受到1个较大的接触压力。因此,接触面积小于临界值的微凸体受到的压力较大,更容易发生塑性变形;而接触面积大于临界值的微凸体受到的压力较小,不会发生塑性变形。目前为止,这种非常规的接触行为依然被许多研究者所采用。
根据上述理论,单个微凸体与刚性光滑平面接触的法向接触刚度kn、切向接触刚度kt分别为
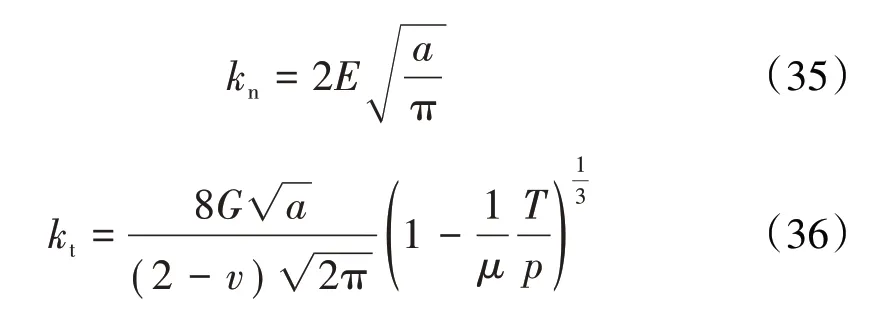
式中:G为接触面2种材料的等效剪切模量;υ为接触面2种材料的泊松比;μ为摩擦系数;P为微凸体所受的法向载荷;T为微凸体所受的切向载荷。
根据微凸体面积分布函数得到总的接触刚度为
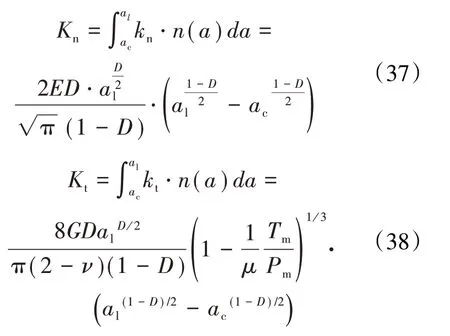
2009年,温淑花等[56-57]基于分形理论引入以微凸体变形位置截面积a'为变量的接触面积分布函数n(a'),建立了考虑区域扩展因子的结合面接触刚度分形模型
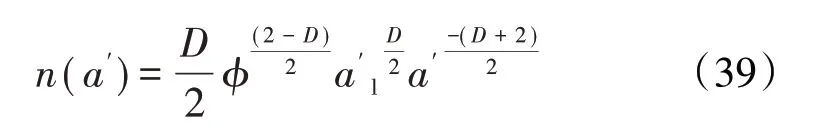
式中:φ为区域扩展因子;a'为微凸体接触截面积,其与真实接触面积之间的关系为a'=2a。
整个结合面的法向接触刚度、切向接触刚度分别为
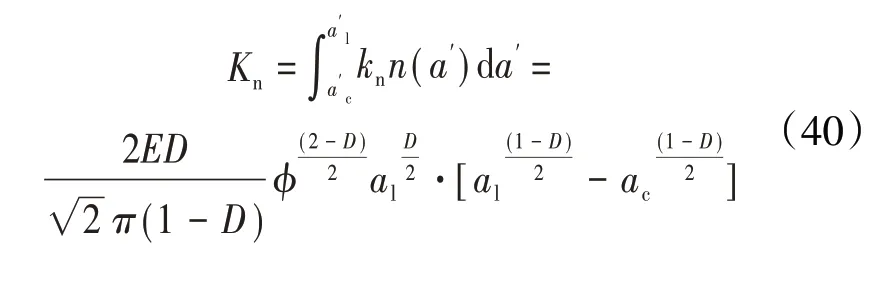
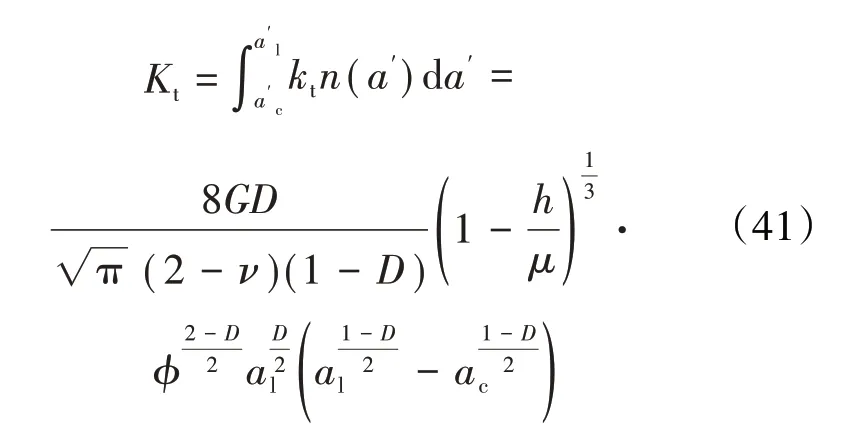
3.3 考虑弹性、弹塑性及塑性的分形接触刚度模型
2015年,张学良等[58]基于分形理论、MB模型及KE模型,分别计算了微凸体变形处于4个阶段(弹性变形阶段、第1弹塑性变形阶段、第2弹塑性变形阶段、塑性变形阶段)时的接触刚度,建立了更符合实际情况的结合面法向接触刚度分形模型。单个微凸体不同阶段的法向刚度分别为
弹性阶段的法向刚度
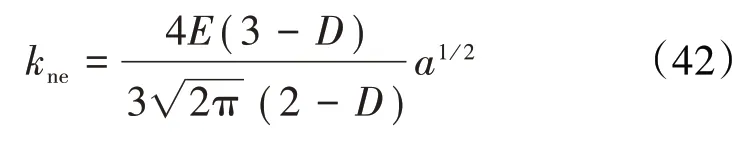
第1弹塑性阶段的法向刚度

第2弹塑性阶段的法向刚度
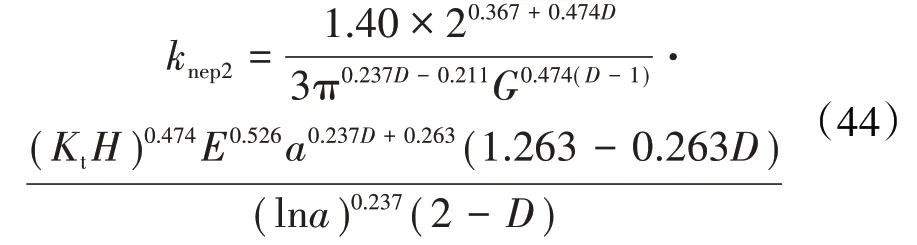
处于完全塑性的微凸体不具有法向刚度,则结合面总的法向接触刚度为

式中:ac为微凸体变形量为ωc时的接触面积。
2018年,陈建江等[59]基于分形理论建立了一种粗糙表面加卸载力学解析模型。推导出了单个微凸体变形处于不同阶段(弹性变形阶段、弹塑性变形阶段和塑性变形阶段)的条件。引入了频率指数,并总结了不同频率指数所对应的微凸体面积密度分布函数。王颜辉等[60]基于上述理论得到了微凸体处于各变形临界阶段时频率指数的大小,建立了频率指数大小不同时的结合面接触刚度模型。
4 有限元接触刚度模型
随着有限元技术的发展,越来越多的学者开始采用有限元方法建立接触模型,弥补解析模型的不足。
2012年,杨国庆等[41]通过3D粗糙表面数字化表征方法,获得了具有不同统计特征的高斯或非高斯粗糙表面,并分析了其接触特性。
2017年,孙伟等[61]基于有限元方法提出了一种结合面法向接触刚度多尺度计算方法。该方法在仪器测量的形貌数据基础上,采用小波分析技术获取了更加真实的形貌,并基于有限元微观接触分析建立了局部压强与基础刚度的关系。基于有限元宏观分析得到压强分布,进而得到结合面接触刚度。实现了接触刚度从微观到宏观的跨越。
2018年,吴少雷等[62]基于Matlab与Ansys构建出3维随机表面,简化了粗糙表面建模过程,完成了粗糙表面参数化建模。
2021年,伍伟敏等[63]基于车削运动原理,采用Abaqus建立了3维车削粗糙表面接触模型,得到了法向接触刚度有限元结果。为计算车削表面法向接触刚度提供了一种新方法。
5 未来研究方向
随着航空发动机技术的逐渐进步,发动机整机的稳定性愈发重要,如何提高发动机稳定性将成为制约发动机技术进步的关键因素。本文从接触刚度的角度出发,提出以下3个研究方向,为今后航空发动机技术发展提供借鉴。
(1)纳米级粗糙表面接触刚度模型。随着机械零件加工技术的不断进步,零件的尺寸已经达到纳米量级,零件的尺寸与微凸体的尺寸将同处于这一量级,材料的刚度性能将呈现出微尺度效应,在今后的建模过程中,如何考虑这种尺度效应,是接触刚度建模的重要研究方向。
(2)考虑基体变形的粗糙表面接触刚度模型。不管是统计描述接触刚度模型还是分形描述接触刚度模型,都忽略了材料基体变形对微凸体变形的影响。而在真实的接触过程中,粗糙表面的基体和其上的微凸体都会产生形变,基体的变形对微凸体的接触刚度计算有不可忽视的影响。只有将二者结合起来分析,才能得到更加准确的接触刚度。在今后的研究中,如何将微凸体变形反映在接触刚度模型中是一个重要的研究方向。
(3)考虑微观接触的宏观接触有限元模型。由于结合面接触刚度解析计算存在大量的简化过程,其计算结果与实际接触状态有很大差异,因此建立完整的粗糙结合面实体模型具有重要意义。随着计算机技术水平的不断提高,应用有限元方法建立的微观粗糙表面接触模型已经成为一种趋势。但受计算能力的限制,很难将整个粗糙面的接触状态表征到宏观模型上。如何将微观接触力学性能反映到宏观接触有限元模型中,也是将来的主要研究方向。
6 结束语
接触刚度一直是影响航空发动机结构稳定性与可靠性的重要参数之一。基于统计学描述的接触刚度计算模型虽日渐成熟与完善,但仍有许多不足之处。学者提出的分形模型可通过分形参数定量地表达总的接触刚度与粗糙度的关系,但并非所有的粗糙表面都具有分形特征。基于纳米级粗糙表面接触刚度模型、考虑基体变形的粗糙表面接触刚度模型、考虑微观接触的宏观接触有限元模型可弥补解析模型的不足,将是接触刚度计算模型的未来发展方向。
