联轴器不对中转子系统的故障再现方法

于清文，王菲，卢良文，罗忠，姜广义

（1.东北大学机械工程与自动化学院，2.航空动力装备振动及控制教育部重点实验室：沈阳 110819；3.中国航发沈阳发动机研究所，沈阳 110015）

0 引言

在航空发动机、汽轮机、压缩机等大型旋转机械中，转子不对中故障是最为常见的故障形式之一。所谓转子不对中通常是指2个相邻的、设计要求本应同轴的转子在实际运行中轴心线出现不同轴。据国内外相关资料分析，旋转机械的振动故障约60%以上都是由不对中引起或与其相关，而联轴器不对中占多数[1]。联轴器不对中会引起转子系统的不稳定运动，进而引起设备振动、轴承磨损、轴挠曲变形、转子与定子碰摩等一系列问题，轻者会影响设备的正常运行，重者会造成设备损坏进而引起更严重事故[2-4]。因此，研究联轴器不对中转子动力学问题，掌握不对中转子系统振动行为的分析理论与方法，不仅具有重要的理论意义，而且具有十分重要的实际应用价值。在工程实际中最有效的研究方法是物理试验，而直接采用原型系统进行联轴器不对中故障机理试验，特别是对于结构复杂且尺寸较大的原型系统试验，存在结构复杂、复现故障难度大、试验成本高以及试验周期长等局限性。因此针对联轴器不对中故障的试验研究，开展其试验模型的动力学相似研究具有重要意义，即用动力学相似试验模型转子系统复现原型转子系统的动力学特性和联轴器不对中故障特征，进而获得原型转子系统的动力学特性和联轴器不对中故障机理。

国内外关于通过动力学相似模型转子系统再现联轴器不对中故障研究的报道尚不多见，多为动力学相似转子系统的特征预测和不对中故障机理及试验研究。Young[5]针对船用发动机转子系统，推导了动力学相似关系，建立了转子叶片的实体模型和相似模型；Wu[6]建立了完全相似转子系统模型，并利用有限元数值模拟方法对固有频率和响应相似关系进行了验证；殷杰等[7]采用量纲分析法对燃气轮机拉杆转子进行了动力学相似研究，推导了畸变补偿模型与原型的动力学特性畸变相似准则；胡培民[8]分析了完全几何相似转子系统的弯曲振动响应，并研究了支承刚度在转子弯曲振动中的相似律；Sudhakar等[9]总结了联轴器不对中的建模方法，研究了不对中故障的诊断识别方法；Patel[10]通过试验研究了不对中转子系统的振动特性，指出转子不对中并不是出现2倍工频振动响应的惟一原因；万召等[11]比较了转子-轴承系统在考虑联轴器不对中前后的振动响应和稳定性，指出联轴器不对中会引起2～4倍甚至更高倍频振动。

本文考虑由联轴器不对中引起的附加力，建立带有联轴器不对中的转子系统动力学方程并推导转子系统各参数的动力学相似关系，建立满足动力学相似关系的不完全几何相似模型，并进行数值仿真和试验验证。

1 动力学模型

转子不对中主要反映为联轴器不对中，分为平行不对中、角度不对中和综合不对中3种形式。平行不对中是指两半联轴器轴心径向不重合引起的不对中，角度不对中是指两半联轴器轴心线不平行引起的不对中，而综合不对中是指平行不对中和角度不对中综合在一起[12-14]。

1.1 不对中力

1.1.1 由于平行不对中引起的作用力

由于平行不对中引起的作用力如图1所示。o1和o2分别为左右两半联轴器的端面轴心点，不在同一轴线上且存在平行不对中量Δy[14]，Δl为左右两半联轴器的安装距离。

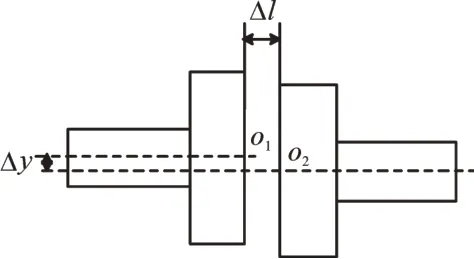
图1 由于平行不对中引起的作用力

将端面轴心点o1、o2沿轴向投影在同一平面内（如图2所示），o1'、o2'分别为投影点，以o1'o2'为直径作圆，设圆心为点o。受平行不对中影响，联轴器的几何中心N的运动轨迹可近似看作是以o1'o2'为直径的圆[14-15]。

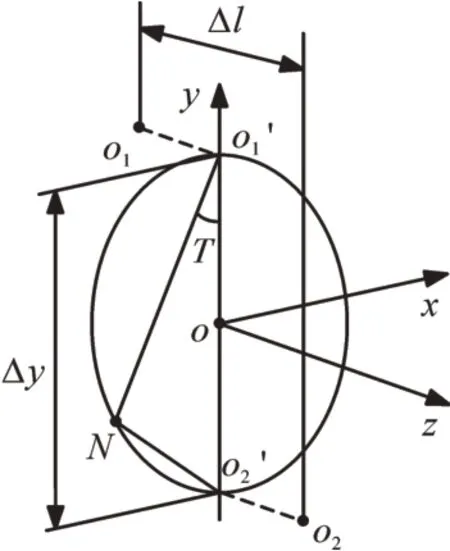
图2 联轴器轴心投影

以圆心o为坐标原点，以o1'o2'所在直线为y轴建立平面直角坐标系oxy，则几何中心N的坐标可表示为N(xN,yN)，设o1'N和o1'o2'的夹角为θ，转子的转速为ω，则dθ/dt=ω。由几何关系可得N点坐标分别为

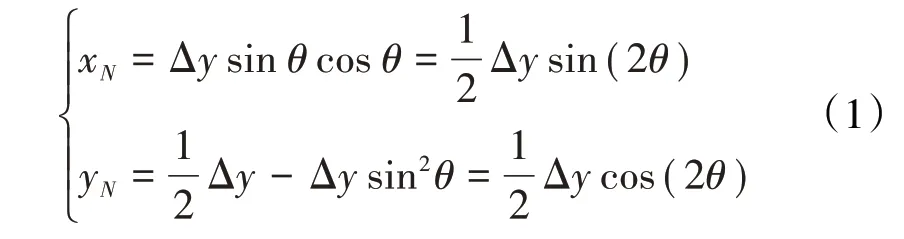
对xN、yN分别求关于t的2阶导数，可得

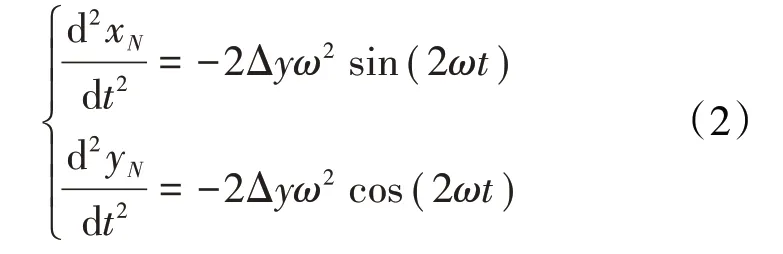
根据牛顿第2定律，在平行不对中的情况下联轴器的不对中力可表示为[15]

式中：Fx、Fy分别为转子在x、y方向上受到的分力；mc为联轴器质量。

1.1.2 由于角度不对中引起的作用力

由于角度不对中引起的作用力如图3所示。当转子存在角度不对中时，左右两半联轴器存在夹角α。

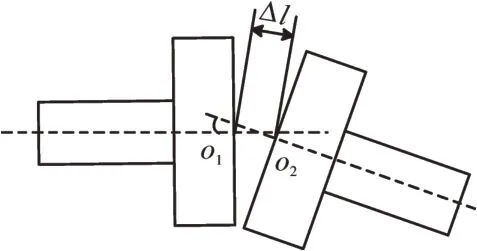
图3 由于角度不对中引起的作用力

左右两半联轴器的运动中心不重合，联轴器在运动过程中受到角度不对中影响，转动的同时发生摆动，运动轨迹如图4所示。

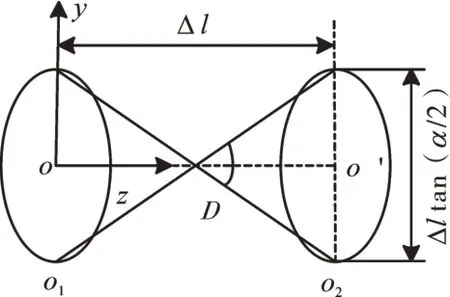
图4 角度不对中运动轨迹

通过几何关系推导可得角度不对中量为Δltan(α/2)，根据平行不对中力的推导思路得到角度不对中产生的不对中力为

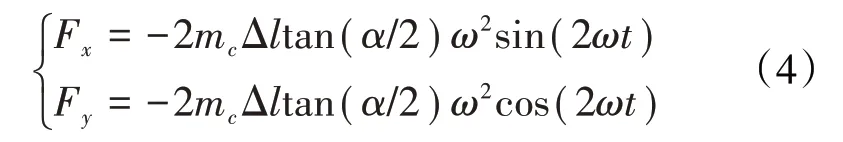
1.1.3 由于综合不对中引起的作用力

当平行不对中和角度不对中同时存在时，即为综合不对中时，若2种不对中故障发生在同一平面，则不对中合力为2种不对中力的代数和，若不在同一平面内，则可通过几何关系算出合力。为方便计算，假设平行不对中量与不对中角在同一平面内，则由综合不对中引起的作用力可表示为[15]

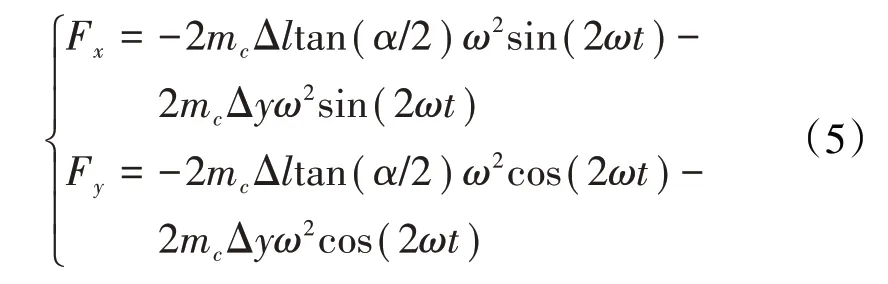
1.2 动力学模型

为了便于研究，建立1个简化的不对中转子系统如图5所示。从图中可见，电动机通过左右两半联轴器与带有1个转盘的轴联接，转轴由2个滚动轴承支承。

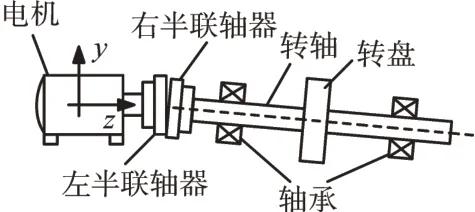
图5 带不对中故障转子系统

不计电动机输出轴的质量，设转轴和转盘的质量为m，阻尼系数为c，转速为ω，左右两半联轴器质量为mc，平行不对中量为Δy，角度不对中量为Δltan(α/2)，其振动方程可表示为

考虑不平衡力和重力，结合式（6）可得到动力学方程[2，16]

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Fe为不平衡力；Fr为不对中力；G为重力；q、˙、分别为水平竖直方向的响应向量、速度向量及加速度向量

2 相似关系建立

设计相似模型时，首先要获得动力学相似关系，对于模型和原型2个系统对应的各参数都应满足相似关系，即模型和原型各对应参数之间都满足一定比例，把这个比例习惯定义为相似因子。原型和模型在选择相关参数时，材料参数与结构参数等建模需要的参数需按照一定的相似关系给定，而后通过公式理论推导得到响应结果的相似关系。参数选取依据实际建模和结果分析给定，建模所需的必要参数以及要分析的响应参数等。参数选取具有主观性，但不影响适用性。相似因子是确定相似模型设计参数的重要依据。

不对中转子系统的动力学方程为

则原型和模型系统的动力学方程分别为

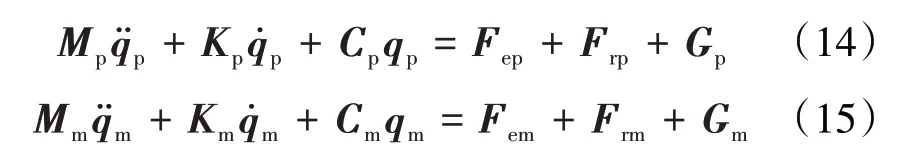
式中：下标p和m分别表示原型和模型。

设式（14）、（15）中各参数相似因子为λε，则

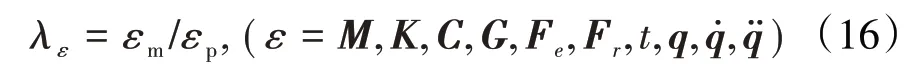
根据式（16）得到各参数的相似因子，见表1。

根据表1结果，式（14）可表示为

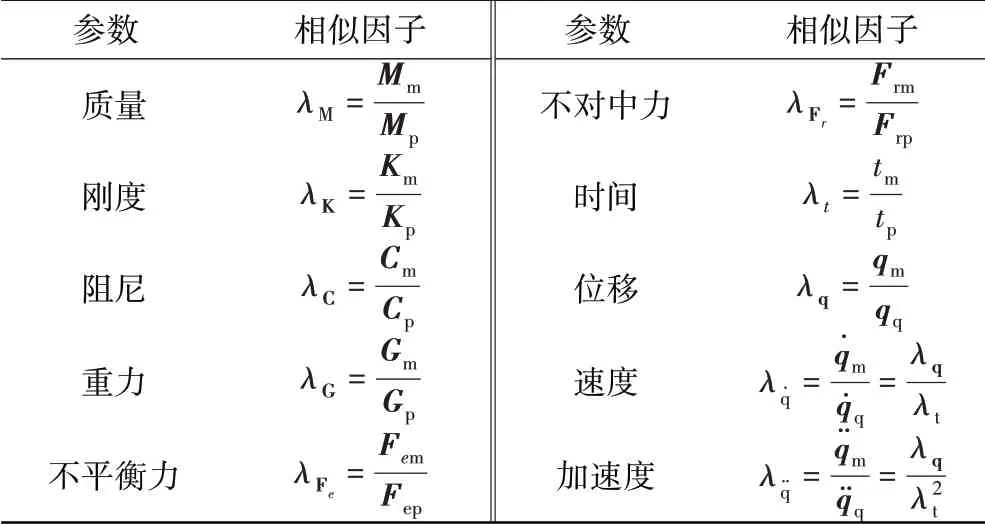
表1 转子系统各主要参数相似关系

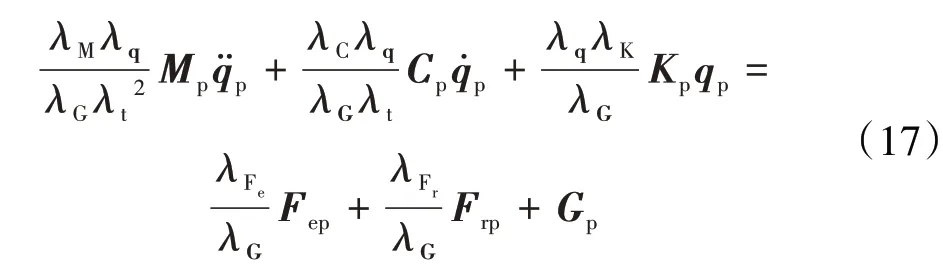
因为式（17）与式（14）等价，可得

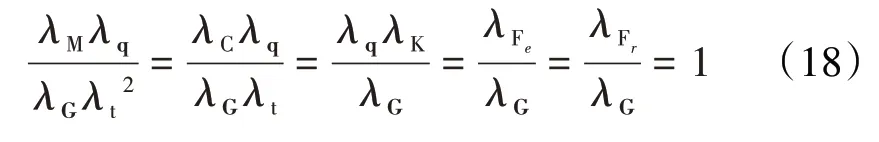
式（18）即为模型和原型转子系统动力学相似关系式。

由量纲分析可知

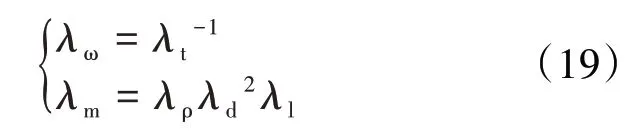
根据式（8）可得

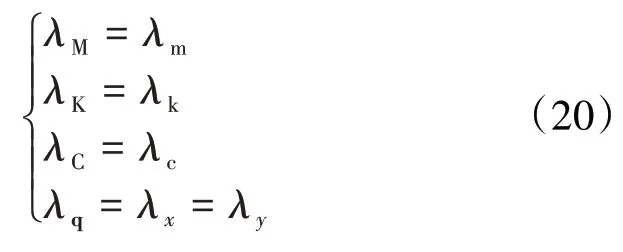
式中：λx、λy分别为水平和竖直方向的响应相似因子。

将式（19）、（20）带入式（18）并进行整理化简

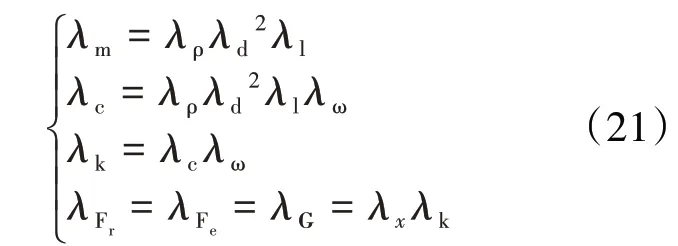
根据文献[17]可知临界转速相似因子λω为

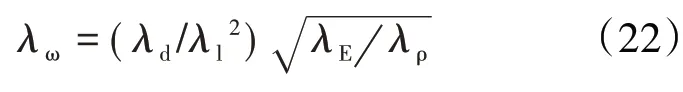
带入式（21）可得

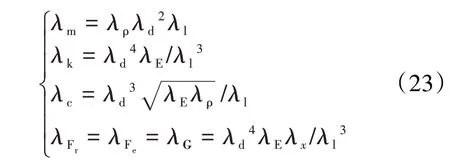
对于不平衡力Fe、不对中力Fr和重力G，相似因子满足各分量式等价

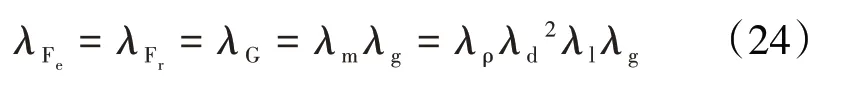
根据式（9）、（10）中不平衡力和不对中力的表达式，推导出不平衡力和不对中力相似因子的表达式分别为

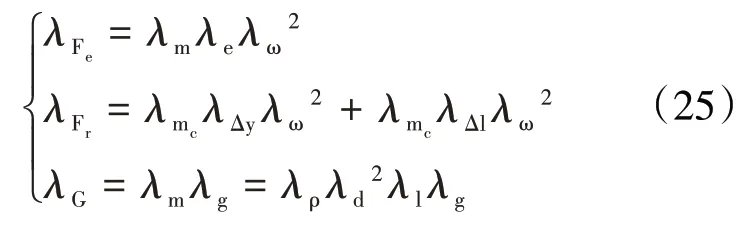
角度不对中力的不对中夹角α为三角函数形式，量纲为1，故λα=1。整理得到方程组

转轴、转盘和联轴器采用相同的质量缩比关系，因此有λm=λmc，化简式（26）得

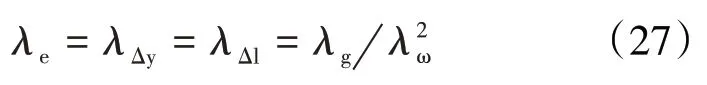
按照上述相似因子设计模型，通过式（21）推导出原型与模型响应的相似因子，由式（18）和式（23）可得

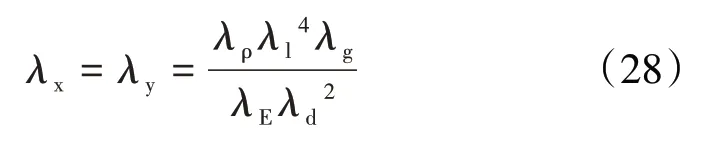
整理得到满足相似条件的相似关系

推导出的系统模型与原型各参数相似因子见表2。

表2 系统模型与原型各参数相似因子

3 算例

为验证所建立相似关系的正确性，进行数值仿真验证。设计1套动力学相似的原型和模型试验系统，模型和原型的材料相同，即λρ=λE=λg=1，且满足临 界 转 速 相 似 因 子λω=1，即 由 式（22）知λl=0.707,λd=0.5，根据式（28）、（29）计算得到各参数的相似因子

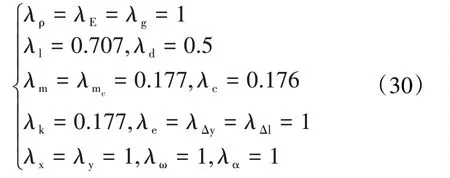
根据式（30）提供的各参数相似因子，计算得到原型和模型的具体参数见表3。

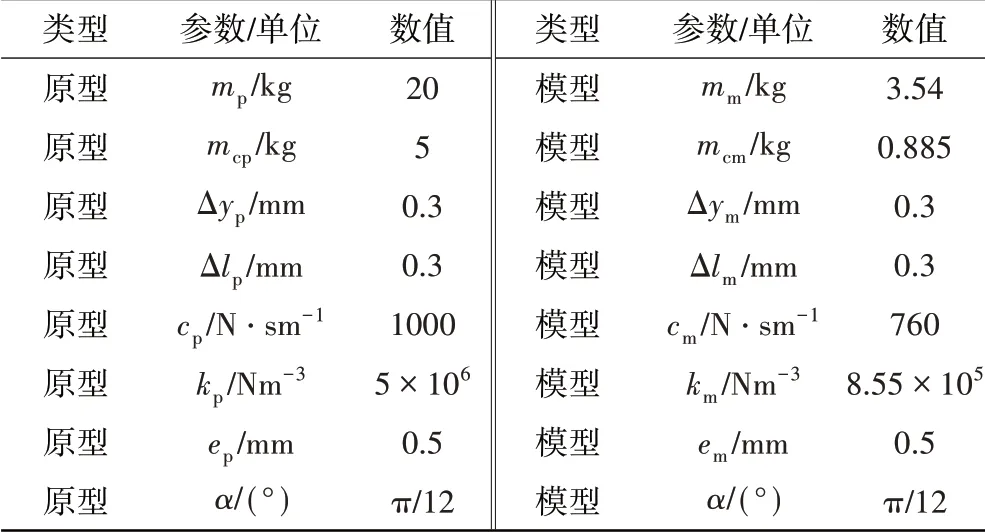
表3 原型与模型转子系统参数

根据表3所列原型与模型转子系统参数，通过有限元方法建立原型与模型的转子系统动力学模型，分别计算600、1100 r/min 2种转速状态下的频谱和轴心轨迹如图6、7所示。

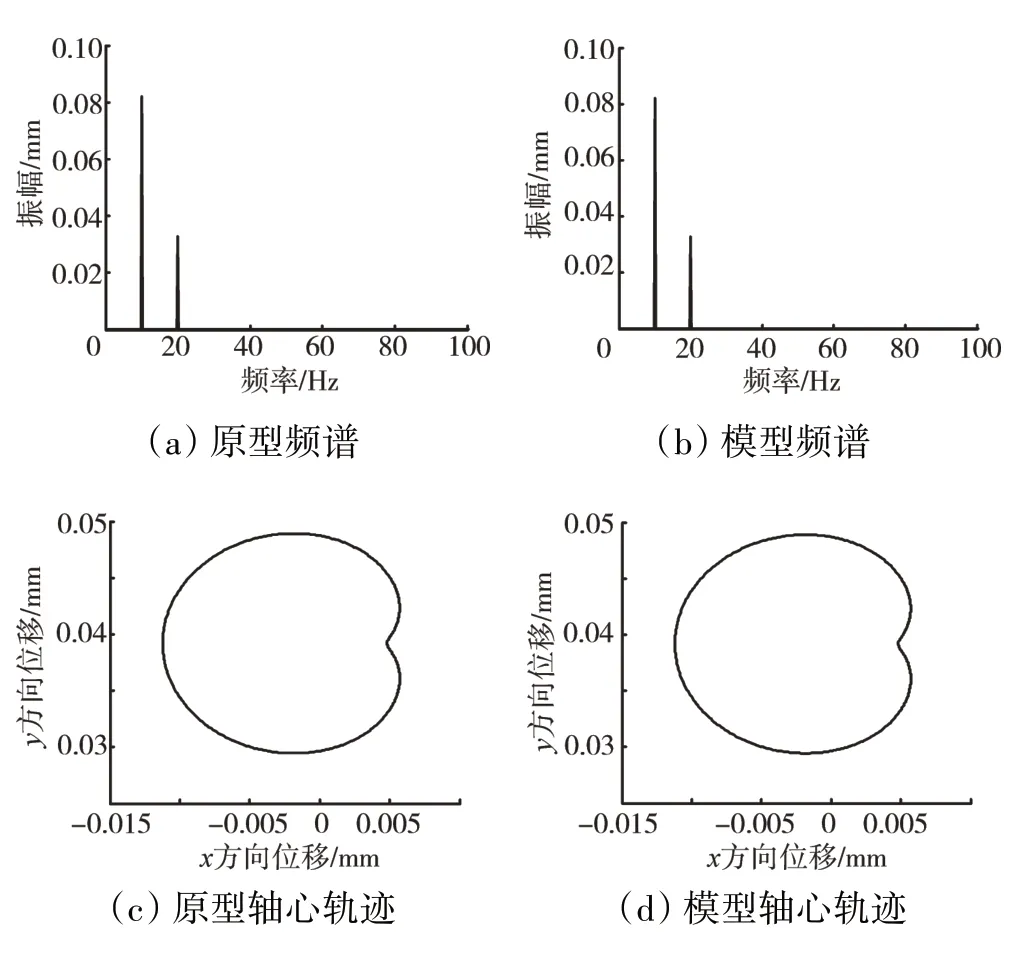
图6 转速为600 r/min的仿真结果

图7 转速为1100 r/min的仿真结果

从图6、7中可见，模型与原型系统均存在2倍频，且频谱和轴心轨迹都满足λω=1、λx=λy=1的相似关系，仿真结果符合设计要求，验证了相似设计方法是正确的。转子系统不对中故障在动力学方程中主要表现为存在不对中力，因此，所提出不对中故障复现相似设计方法，其主要内容在于模型系统的结构参数、材料参数和载荷参数的动力学相似设计。

4 试验验证

为了进一步验证所提出相似设计方法的实用性和有效性，进行试验验证。基于动力学相似设计方法设计2套试验系统分别如图8所示。2个试验台的1阶固有频率设计值为36 Hz，设一套为原型，另一套为模型。试验过程中首先进行试转，通过调频器将电机转速调至1500 r/min后缓慢降为零，然后再正式开展试验。转子转速达到目标转速后稳定1 min之后再进行数据采集。

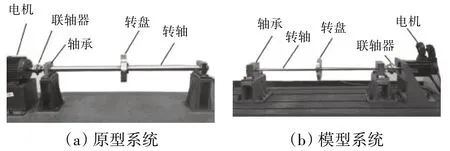
图8 转子试验系统

试验台基本参数见表4。

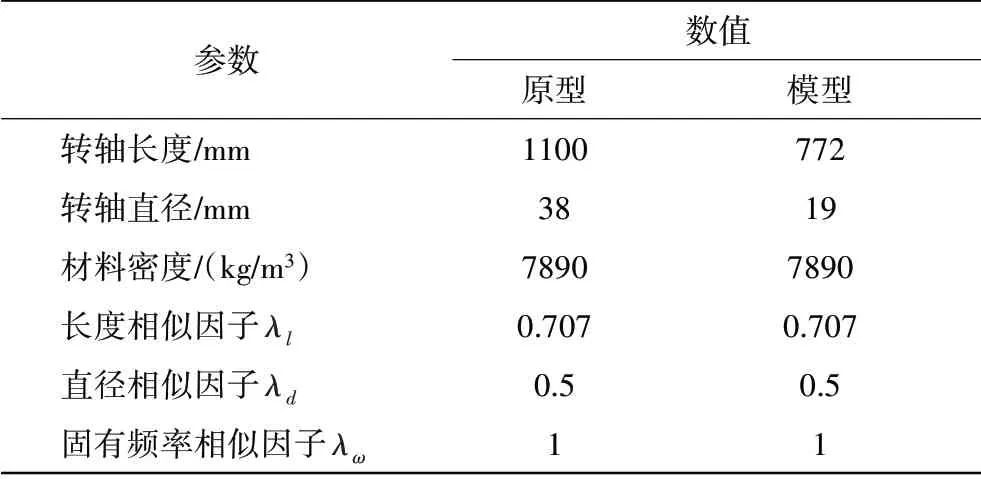
表4 原型和模型试验台参数

通过垫高轴承底座模拟联轴器不对中，由于不对中量和安装距离的相似因子λΔy=λΔl=1，故2个试验台的垫高比例相同。使用电涡流位移传感器分别测试转子系统的水平和竖直方向位移，测点布置于联轴器与转盘之间的转轴上，原型系统测点在距离转盘左侧100 mm处，模型系统测点在距离转盘左侧77 mm处。分别对比600、1100 r/min 2种转速下的轴心轨迹和频谱响应，如图9、10所示。

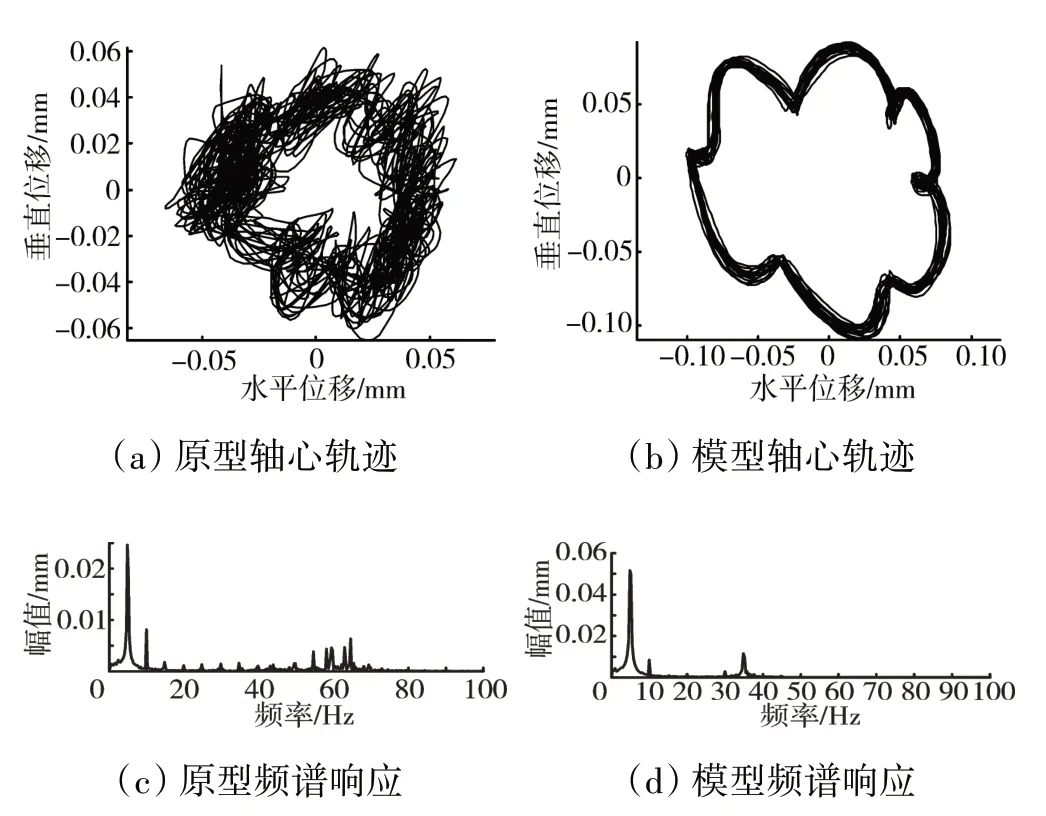
图9 转速为600 r/min的轴心轨迹和频谱响应

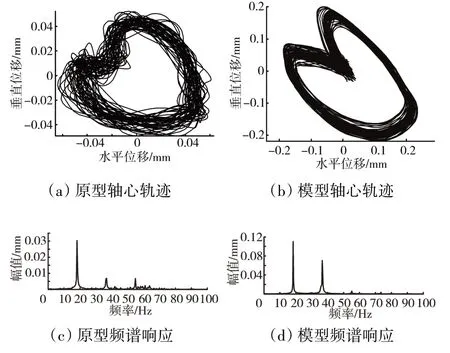
图10 转速为1100 r/min的轴心轨迹和频谱响应

从图9、10中可见，模型与原型系统均存在2倍频，模型与原型系统的轴心轨迹保持较高的相似度。且频谱满足λω=1的相似关系，验证了相似设计方法的实用性和有效性。在实际应用中，首先选定相似模型结构尺寸参数的缩比，然后在此基础上，基于动力学方程和相似理论，开展模型系统结构简化设计，以及材料参数、载荷参数和边界条件参数的相似关系确定。从图9、10还可见，2个试验台的频谱与轴心轨迹均存在较好的一致性，但由于试验台加工误差、装配误差等原因，动力学特性很难保证完全一致，因此，对于复杂系统需要对动力学相似关系进行修正。

5 结论

（1）采用方程分析法和量纲分析法相结合，对联轴器不对中转子系统进行动力学相似分析，建立了联轴器不对中转子系统的动力学相似关系。

（2）利用所建立的动力学相似关系，利用模型转子系统试验结果预测了原型联轴器不对中故障，研究了转子系统联轴器不对中的故障机理。

通过试验验证发现，研制动力学相似模型试验台时，由于系统刚度与阻尼等一些复杂参数无法完全与理论设计值保持一致，还容易受到支承刚度等因素的影响，因此，实测位移响应会随着转速的提高与理论值出现偏差。所以在设计较复杂的转子系统模型试验台时，需要进一步分析响应的影响因素及其灵敏度，并对响应相似因子进行修正。