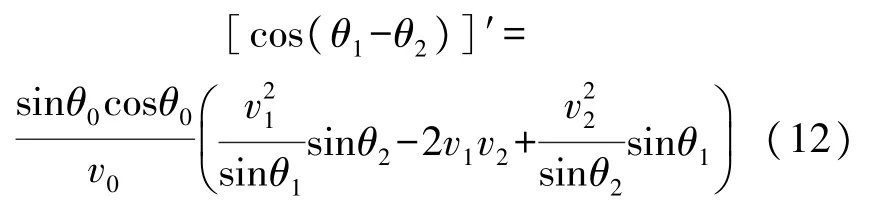深水多波束声纳的快速声线追踪方法*
2022-02-04汤巧英黄智才
汤巧英,黄智才
(1.浙江同济科技职业学院经济与信息学院,浙江 杭州 311231;2.浙江大学地球科学学院,浙江 杭州 310027;3.地理与空间信息研究所,浙江 杭州 310027)
多波束测深是当前飞速发展的一项全新的海底地形精密勘测技术。该技术采取广角度定向发射和多通道声纳信息接收,每次发射可获得水下高密度的具有上百个波束的条幅式海底地形数据。随着多波束探测设备的移动,以条幅推扫的方式探测海底地形[1-6]。由于海水的作用,探测声波波束在海水中不是沿着一条直线进行传播,由于在不同介质层界面都会发生反射和折射,因此实际探测声波波束在海水中是一条曲线。为了能够反演计算波束脚印的真实位置,就必须反演出声波波束的实际传播路径,也就是根据声速剖面(不同深度的实际声速信息)进行声线追踪,计算出波束脚印距离波束发射点的水平相对位移和垂直相对位移[7-12]。
在多波束声纳系统中,对测深数据的实时反演与显示是其一项重要任务。其目的是帮助声纳操作者和研究人员及时了解海底地形起伏信息,提高现场决策能力。因此,基于声线追踪的波束脚印快速解算是保证多波束声纳系统正常执行测绘任务的基本条件。然而声速的采样信息直接决定了声线追踪的计算精度,因此快速声线追踪方法需要在计算精度与计算效率之间做出有效平衡,能够同时保证准确性和运行时间的双重需求[13-17]。波束脚印位置虽然是根据声纳波束的传播路径及往返时间确定,但是由于海水是非均匀的介质,声速在深度方向上变化很大,导致声波的传播路径是不规则的连续曲线。因此,声线追踪的基本原理是把海水分成n 层,每层对应特定的声速(即声速剖面),根据Snell 定律可以计算出每层的声纳波束指向角,从而追踪声波的传播路径,最终逐层计算出波束脚印的位置。目前常用的声线追踪方法有以下3 种:①常梯度声线追踪法。该方法假设声速剖面中两个相邻采样点之间的声速为固定梯度的线性变化[1,18-19];②常声速声线追踪法。该方法假设声速剖面中两个相邻采样点之间的声速是固定不变[1,18];③等效声速剖面法。该方法的原理是波束脚印位置误差仅与入射角和相对面积差有关,因此可以找到一条相对简略的声速剖面取代原始精细声速剖面进行计算[18-20]。很显然,声速剖面越精确则声线追踪结果越精确。在深水多波束实际作业过程中,为了尽可能提高测量精度,声速剖面中的采样点数量通常会达到几百甚至上千,导致声线追踪计算量巨大。上述方法中,常梯度方法最能精确刻画声速变化,因而计算结果精度最高,但是计算量较大,计算效率较低。常声速方法虽然简化了声速变化,但是声速剖面中每个采样点仍需计算,因此计算量仍然较大,同时计算精度也会明显下降。等效声速法虽然能有效简化声速剖面,兼顾计算效率与精度,但是该方法在寻找等效声速剖面时依然面临很大挑战,必须预先获取作业海域的参考深度,且不适用于海底地形起伏较大的区域[21-23]。
为了兼顾计算精度与效率,本文采取了一种简化声速剖面以减少声速采样点的策略,提出了一种快速声线追踪方法,该方法利用经典道格拉斯-普克算法对声速剖面(声线追踪的唯一参数)进行简化,并且对因声速剖面简化所引入的误差进行有效控制,使得简化声速剖面的声线追踪结果能同时满足精度与效率需求。
1 原理
1.1 声速剖面特征分析与简化机制
声速剖面是指海水中声速随深度变化的信息,反映声速在海水中的变化规律。海水中声波的传播速度受到海水温度、盐度和压力等因素的影响而发生改变。通常情况下,声速在一定水平面范围内变化不大,主要是在垂直深度方向上发生剧烈变化,呈现出以下规律[24-25](如图1 所示):

图1 声速剖面的典型特征
①在海平面到水下几米(或数十米)的深度范围内,由于受到太阳辐射的影响,该范围中的海水温度基本是恒定的,而海水的静压力则随着深度的增加而增加,因此声速也随着深度的增加而缓慢增大;
②在几十米到几百米范围中,是一个温度跃变层,在此范围内,温度是影响声速最主要的因素,其影响远远超过海水静压力。由于温度随着海水深度的增加急速下降,声速会呈近似线性的减小;
③在几百米以下区域为深海等温层,在该范围内,温度处于恒定,这时,海水的静压力是影响声速变化的主要因素,在这个范围内,声速会随着深度增加呈近似线性的增长。
一般情况下,要想准确反演波束脚印(即声波与海底界面的交点)位置,就需要根据声速剖面进行声线追踪。根据Kinsler 和Frey 的证明[26]:当声速呈线性变化时(即声速梯度为固定常数),波束的传播轨迹为一段圆弧,如图2 所示。图中θi-1是波速传播速度为vi-1时的掠射角,θi是波束传播速度为vi时的掠射角;gi为声速梯度,Ri为圆弧半径,这两个参数的计算公式为:
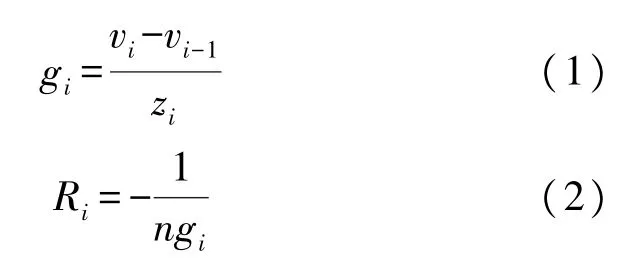
式中,n为Snell 常数。根据图2 中的几何关系,可以得到波束在该范围中的水平位移yi和垂直位移zi:

图2 常梯度声速介质中波束传播轨迹
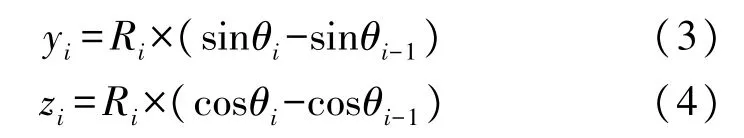
由此可知,根据上述声速剖面的变化特征,对于声速随深度呈线性变化的部分(温度跃变层与深海等温层),波束的水平位移和垂直位移可以直接通过式(3)、式(4)计算获得;进而可以得到,在声速呈线性或类线性变化的部分,对声线追踪结果形成主要影响的是该部分首尾数据点,而在首尾之间的数据点对于声线追踪的最终结果影响小。
根据上述分析,本文快速声线追踪方法的主要策略就是剔除声速剖面中的冗余数据点:对于声速剖面中声速随深度呈线性或类线性变化的部分(如温度跃变层、深海等温层)进行数据抽稀处理,保留对声线追踪结果影响较大的数据点(如线性变化部分的首尾点),而剔除对结果影响微小的数据点。通过简化声速剖面,减少声速采样点,以降低声线追踪的计算量,从而提高计算效率。
1.2 声速剖面简化误差分析
上述声速剖面简化机制虽然可以很好地保持声速剖面的整体变化特征,但是对声速快速非线性变化部分的简化(减少声速采样点)势必会造成原始数据信息丢失,从而导致声线追踪的计算结果产生误差,即快速声线追踪是以牺牲计算结果精度为代价的。为了有效控制因声速剖面简化处理所带来的误差,保证声线追踪结果满足准确性需求,还需要对计算误差进深入分析,以明确误差产生的影响,从而进行有效的误差控制。本文通过分析并证明,得到了以下结论:声速剖面经过简化后,导致的声线追踪误差由中心波束向边缘波束线性依次增大(具体证明过程见附录)。换言之,只要边缘波束的声线追踪结果满足准确性需求,那么其他波束的计算结果必然满足需求。因而,对声速剖面进行简化处理时,只需控制边缘波束的声线追踪结果(相较于未简化的原始声速剖面)在满足准确性需求的基础上尽可能地减少声速采样点,就可以得到最佳的声速剖面简化结果,从而使声线追踪兼顾效率与准确性。
2 方法
2.1 声速剖面简化处理
根据声速剖面的特征以及其简化机制,其简化过程为:保留声速剖面中反映其变化特征的数据点(即声速剖面曲线中的主要形值点),而剔除其他位于线性变化中的数据点(主要是温度跃变层与深海等温层中的声速线性变化数据点)。从数学角度而言,这个过程即为矢量数据的抽稀处理。为了保证简化处理的效率和效果,本文采用道格拉斯—普克算法[27]这一经典曲线化简算法,对声速剖面进行简化处理。其基本原理是首先将声速剖面作为一条完整的线段取首尾两端点,然后计算线段内其余各点到连接两端点的直线的距离。如果这些点到该直线的垂直距离中最大者仍小于事先给定的阈值,则两端点间的数据点均被舍去;如最大距离大于给定阈值,则将此点保留,并以此点将原来的线段分为两段,对这两段重复上述过程,分别检验最大垂距是否大于阈值,重复此过程直到没有多余的点需要被舍去为止。如图3 所示,对于连续曲线ABCD,求曲线上各点(除A、D 两点)到AD 连线的距离最大值dMax,若这个最大值小于事先给定的阈值k,则连续曲线就由AD 两点的连线取代,其余点均被舍去。否则,则留下该点。图3 中B 点为曲线上选中的抽稀点,然后分别再找出AB 及BD 上满足最大距离大于k的点,以此下去,直到找不到这样的点为止。因此,根据道格拉斯-普克算法的原理,只需设定合适的阈值k,就可以有效减少声速剖面中的声速采样点。经过简化的声速剖面保留了反映声速变化特征的数据点,而剔除了温度跃变层与深海等温层中对声线追踪结果影响较小的数据点,降低了声线追踪的实际计算量。
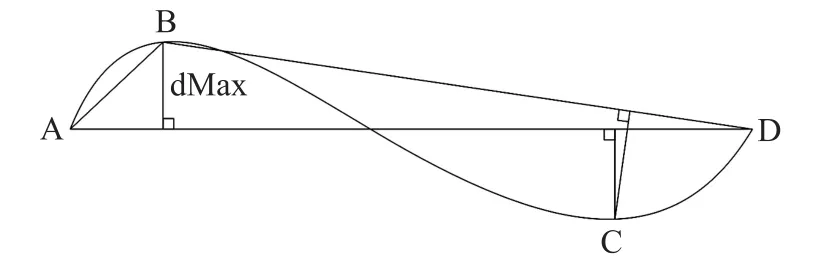
图3 道格拉斯-普克算法基本原理示意图
2.2 基于“反馈”机制的误差控制
采用道格拉斯—普克算法进行声速剖面简化时,需要设定抽稀(简化)阈值k。k值越大,保留的特征点(声速采样点)越少,声线追踪计算量越小、效率提高越多,但由于原始数据中信息丢失过多,会给计算结果带来更多误差;k值越小,所保留的特征点(声速采样点)越多,声线追踪计算量减少不多、效率提升不高,但由于原始数据中信息丢失较少,导致计算结果误差也较小。因而,为了兼顾声线追踪的效率和准确性,声速剖面的简化阈值k至关重要。但是道格拉斯-普克算法的阈值设定无法满足上述要求,具体体现为:由于道格拉斯-普克算法中抽稀阈值k的含义为点到直线段距离,其难以与声线追踪之间形成明确的物理联系,因而使合理的阈值设定变得十分困难。
针对以上问题,本文提出一种由“允许误差”反向确定简化阈值的方法,即设定最大允许误差。通过误差反馈与阈值自适应调整机制确定最佳简化阈值。由于在多波束测深精度评价标准中,对于误差并不是直接评价其绝对值大小,而是误差值与对应水深值的比值。根据国际海道测量组织(International Hydrography Organization,IHO)的规定,当海水的实际深度与计算深度之差小于4z‰(z为实际深度)时满足测量精度要求。由于波束脚印位置信息包括了深度值和相对水平位移,衡量其位置的精度时应兼顾水平位移误差和深度值误差,因此本文在进行精度评价时,采用两者的空间位置偏差Δd作为评价指标。本文将声速剖面简化后的边缘波束误差定义为e,其计算公式如式(5)所示。e值直接决定了一定水深下的最大允许误差。

式中,z为水深值,Δd表示在水深为z时,由原声速剖面与抽稀简化后声速剖面所计算得到的波束脚印空间位置的偏差。
上文已经证明声速剖面简化对于边缘波束的影响最大。因此,只需控制边缘波束的误差即可满足精度要求,其具体处理流程为(如图4 所示):

图4 基于“反馈”机制的误差控制流程
①设定边缘波束的掠射角angle、允许误差e和初始声速剖面简化参数k(即道格拉斯-普克算法中的抽稀阈值);k可以取大于零的任意实数,其取值最终取决于允许误差e:e越大,表示最大允许误差越大,声速剖面中可以剔除的数据点越多,k值越大,反之亦然;
②以未经简化处理的声速剖面为基准声速剖面,计算波束到达声速剖面上各个数据节点所对应深度zi(i=1,2,…,n)的时间ti(i=1,2,…,n),并计算出波束在特定深度的水平位移yi(i=1,2,…,n),其中,n是基准声速剖面的层数;
③根据简化参数k对声速剖面进行处理,由简化后的声速剖面和时间ti,计算出波束在时间ti到达的深度z′i和水平位移y′i,得到简化前后深度值和水平位移的偏差:

由此可得到两者的空间距离偏差:
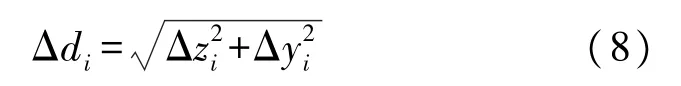
则在一定深度下,两者之间的误差为:

④通过比较得到ei的最大值emax,比较emax和e之间的大小,如果emax大于e,说明k值过大,则减小k值;如果emax小于e,表明k值过小,则增大k值(k值增减采用区间二分法),并返回步骤(3)。如此迭代,直至k值的前后两次变化幅度小于规定范围,即得到了最佳的声速剖面抽稀参数k;由于抽稀参数k与声线追踪误差e呈单调关系(k值越大则误差e越大,k值越小则误差e越小),所以通过该迭代过程可以寻找到允许误差emax范围内的最大抽稀参数k。
⑤根据参数k对声速剖面进行简化处理,并以简化后的声速剖面为声线追踪的参数,完成声线追踪的迭代计算。
3 实验与分析
用VC++编程实现了所提出的快速声线追踪方法,并以3 条采集不同海域的声速剖面(如表1 所示)为实验数据进行对比实验,用以证明本文方法既能提高声线追踪的计算效率,又能保证其计算精度。

表1 对比实验的声速剖面信息
在声速剖面简化处理时,设定的阈值为1‰(即声速剖面简化处理后引起的误差不能超过对应水深值的1‰),简化前后声速剖面的对比如表2 所示。表2 中的对比结果表明:简化前后声速剖面的相关性都大于99.9%,这说明简化后的声速剖面很好地保持了声速变化趋势(只剔除了对声线追踪结果影响微小的数据点),同时经过数据点抽稀,简化后的声速剖面数据量降低了2 个数量级,这将大幅减少声线追踪的计算量,从而提高声线追踪的计算效率(见表3 所示:处理单ping 数据所需的时间)。由于深度不同主要影响的是声速剖面中采样点的数量,因此深度越深,声线追踪所需要的时间越多。可以看出,由于简化后的声速剖面采样点已经非常少,因此声线追踪所需要的时间非常短,相比原始声速剖面,其计算效率提高了约10~100 倍。
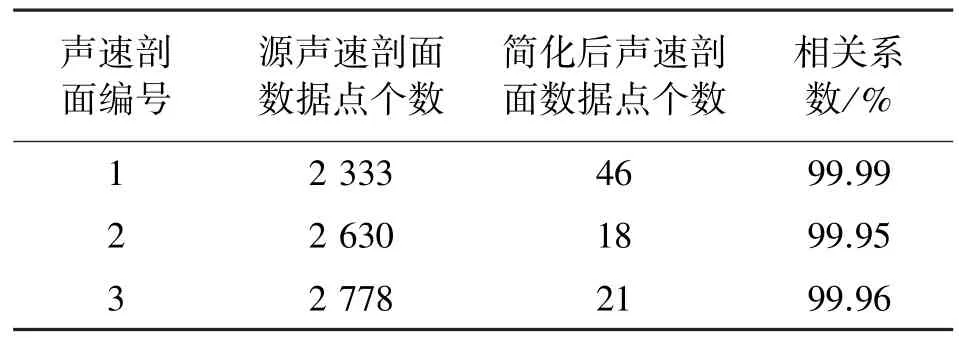
表2 简化前后声速剖面对比
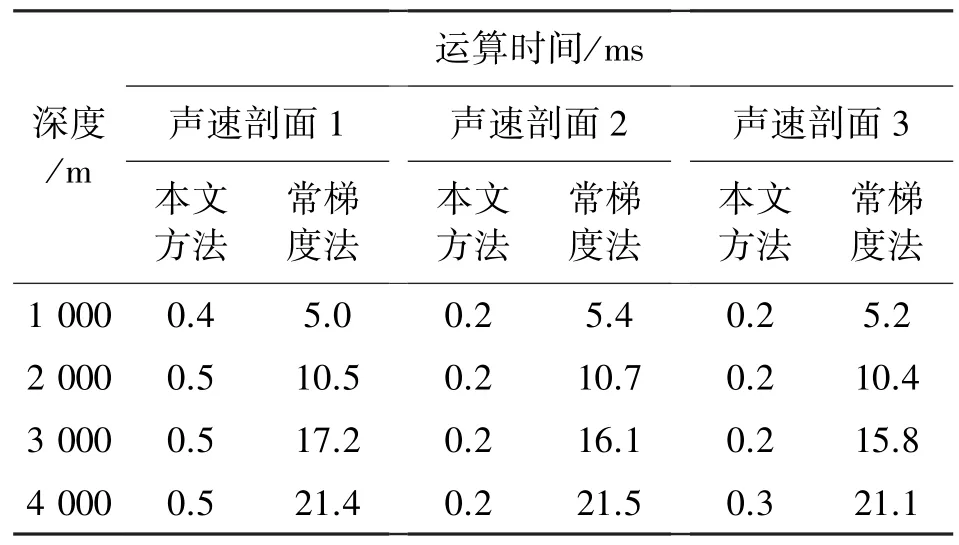
表3 方法效率对比
为了便于说明,本文将根据原始声速剖面计算得到的结果称为“基准值”,根据简化后的声速剖面计算得到的结果称为“计算值”,两者之间的差异表示了由于声速剖面简化而产生的误差。由表2~表6 的对比结果中可以看出,本文对声速剖面进行简化而产生的误差非常小(小于指定的允许误差1‰)。这证明本文提出的基于“反馈”机制误差控制方法能够有效且可靠地寻找到最佳抽稀参数,从而在声速剖面简化过程中保证了声线追踪计算结果满足精度需求,同时又最大限度地减少了声线追踪的计算量,提高了计算效率(如表4~表6 所示)。

表4 本文方法计算精度(声速剖面1)

表5 本文方法计算精度(声速剖面2)

表6 本文方法计算精度(声速剖面3)
4 结论
由于声波在海水中的速度受到多种水文因素的影响,导致其在海水中的传播轨迹是一条复杂的曲线。利用声纳探测海底,首先要对声纳的声波波束进行声线追踪,反演其准确的波束脚印位置。在测量作业过程中,为了提高现场分析决策能力,需要实现快速准确的声线追踪方法。为了监督声线追踪的效率与精度,提出了一种快速声线追踪方法。该方法通过对声速剖面的合理简化,大幅降低了声线追踪的实际计算量,提高了计算效率。同时通过基于“反馈”机制的误差控制方法,有限约束了声速剖面简化处理,保证了声线追踪精度控制在合理范围。实验结果表明,该方法能够有效简化声速剖面,满足声线追踪计算精度与计算效率的实际需求。
附录
证明 声速剖面简化对边缘波束的声线追踪计算精度影响最大。
设原声速剖面为SSP1,抽稀后声速剖面为SSP2,根据Geng 和Zielinski 的研究,对于给定的深度zB,可以找到SSP1的等效声速剖面SSP1eq,SSP2的等效声速剖面SSP2eq,设SSP1eq的斜率为g1,SSP2eq的斜率为g2。在声速呈线性变化的介质中,波束的传播轨迹是一段圆弧,圆弧的曲率半径为R=在深水条件下,等效声速剖面的声速变化率非常小[1],由此可以得到以下的结论:该圆弧的曲率非常小,圆弧非常平缓,同时,由于声速的变化幅度小,根据Snell 定理可知,波束掠射角变化小,则圆弧对应的圆心角非常小,所以可用该段圆弧所对应的弦近似表示波束的轨迹,如图5 所示。

图5 波束传播轨迹
但此时波束的掠射角不再是θ0,对于SSP1eq其波束的掠射角为,对于SSP2eq其波束掠射角为,θ1和θ2分别是SSP1eq和SSP2eq所对应的波束到达层底时的掠射角。这样,根据给定深度zB,可以根据声速剖面SSP1eq和SSP2eq分别计算出波束到达深度zB所需时间:
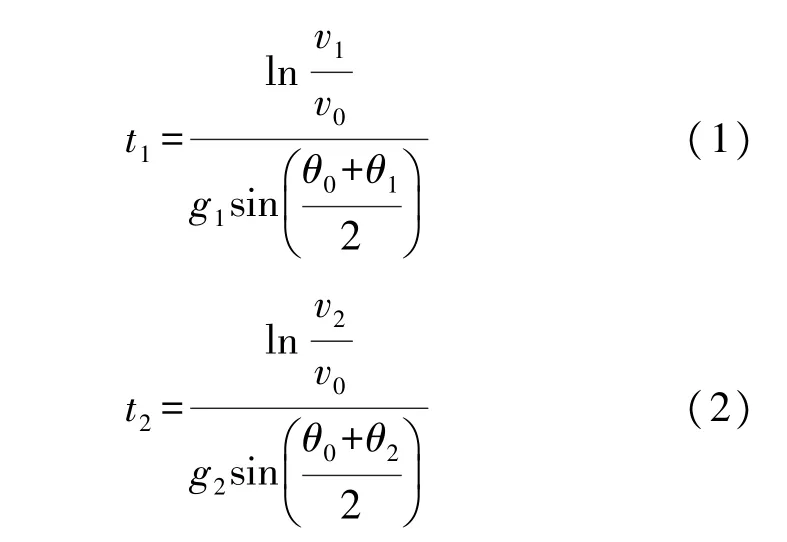
式中,v1,v2分别是波束到达层底时的声速。进一步,根据给定深度zB以及t1和t2,分别计算出波束在此过程中的平均声速,即:



当到达层底时,波束的空间位置偏差为Δd=,将式(5)、式(6)代入,经过化简整理,可得到:


将式(8)~式(11)代入cos(θ1-θ2)中,并对其关于θ0求导,可求得导数为: