蓄电池组充放电温度与应变光纤光栅监测系统研究*

宁垚戬，高 妍*，张红娟，王 宇，白 清，靳宝全

(1.太原理工大学电气与动力工程学院，山西 太原 030024；2.太原理工大学新型传感器与智能控制教育部与山西省重点实验室，山西 太原 030024)

蓄电池组作为不间断电源的储能装置，是各大机房数据中心安全稳定工作的重要保障，蓄电池组的故障往往是机房火灾的罪魁祸首，蓄电池起火通常是连接松动、漏液、热失控、极板生长等因素造成的，连接松动会引起局部电阻增大、发热异常，造成外壳变形、炭化；漏液可能造成蓄电池组间短路；热失控、极板生长会引起电池外壳软化，造成蓄电池鼓包、胀裂、漏液等火灾隐患[1]。所以对蓄电池组充放电温度与应变的监测对及时排查火灾隐患、减少蓄电池导致的机房事故具有极高的实用价值。光纤光栅对温度与应变具有很高的敏感特性，且相比于现有的基于电子式传感器的蓄电池监测系统，光纤光栅还具有光纤本身不受电磁干扰、易于布设、无电传输、耐腐蚀的优势，可以在机房等复杂环境中安全稳定运行[2-3]。因此，设计了基于光纤光栅传感的循环扫描式蓄电池组充放电温度与应变监测系统[4]，相比现有的通过对比同组电池参数差异来发现异常电池的监测系统，本系统不仅可以对比同组电池间的相对温度差，还能监测各单体电池的绝对应变量，更适合于蓄电池组的监测。

光纤光栅传感器(FBG)自问世以来，凭借其远高于其他传感器的性价比，已经广泛应用于电气工程[5]、隧道结构[6]、航空航天[7]、船舶结构[8]等各大领域，光栅的中心波长会随外界物理量的变化发生漂移，所以快速准确的波长寻峰算法是精准解调的必要条件[9]。目前，常用的寻峰算法有直接比较法、多项式拟合法、质心法、神经网络、遗传算法、高斯曲线拟合法等。直接比较法运算速度快，但是仅适用于寻找单峰，且易受噪声影响[10]；多项式拟合法思想简单、容易实现，对于少量数据拟合很有效，但是对于非线性数据、大样本数据的精度较低[11]；质心法误差较大，且容易受到噪声干扰[12]；神经网络精度高，但是训练时间长、计算速度慢[13]；遗传算法精度高、拓展性强，但是算法复杂、计算量大且对初始种群依赖性较高[14]；相比其他算法，高斯拟合法精度高、计算量小、易于实现。考虑到光纤光栅反射信号中经常混杂有非平稳信号，小波去噪可以有效滤除无效信号，但是很难兼顾信号的平滑性与准确性。

因此，本文提出了一种融合改进小波去噪、滑动平均算法和高斯拟合的优化寻峰算法，针对光纤光栅反射的毛刺多、有假峰、近似平顶的信号，改进小波去噪算法，在尽量保留原始信号特征条件下使信号变得平滑，在此基础上用滑动平均算法消除假峰，再对该信号分峰截幅并对每个峰进行高斯拟合。三种算法共同作用，实现对反射信号峰值的准确定位。

1 传感原理及系统搭建

1.1 光纤光栅传感原理

光纤光栅从本质上来说，是对光纤纤芯折射率周期性调制形成的一种无源滤波器，当光在纤芯中传播时，只有满足布拉格条件的光会被反射回来，其余光透过光栅继续传播，其光学特性相当于一窄线宽滤波器。

FBG 的传感原理为[15]:

λB代表反射光谱的中心波长，Λ代表栅格周期，n代表纤芯有效折射率，当外界温度发生变化时，由热光效应和热膨胀效应引起n和Λ发生变化，公式为:

a和b分别为热光系数和热膨胀系数，光栅制成后n、Λ、a、b均为定量，即建立了中心波长变化量与温度变化量的一一对应关系，再用参考温度加以标定，即可测出准确的温度，同理，当外界形状发生变化时，公式为:

Pe为有效弹光系数，n、Λ、Pe为定量，即可建立中心波长变化量与形状变化量的一一对应关系。

以上是单独测量温度或者单独测量应变时的情况，当需要同时测量温度和形状变化时，公式如下:

针对蓄电池组充放电温度与应变监测需要，本系统采用温度补偿的方法，即同时测量每块电池的温度和形变，以此来排除计算形变量时温度的影响，进而测得准确的应变量。

1.2 系统结构

系统拓扑图如图1 所示，光路部分包括C 波段循环扫描激光器及其驱动小板、分光器、环形器、光栅阵列；电路部分包括信号处理模块和采集卡；解调模块主要是上位机。光栅布设在电池组表面和极柱上，上位机可以控制驱动小板，来调节激光器的扫描频率、步长、扫描区间等参数，系统工作时，驱动小板驱动激光器按照设定的参数由低到高循环扫描，同时每周期开始扫描时给采集卡发出触发信号；激光器发出的光依次经过分光器、环形器进入传感场，反射光经环形器传到信号处理模块，调制后的光信号经光电转换模块转换为弱电流信号，经跨阻放大模块转换为易于采集和控制的电压信号，经硬件低通滤波模块降低了干扰信号的影响，最终携带外界信息的信号经采集卡传输到上位机并完成后续解调工作。

图1 系统拓扑图

2 软件解调及算法优化

2.1 软件解调原理

系统软件部分由工控机来完成，主要包括波长标定、待测量解调等工作。本系统采用的是基于循环扫描激光器的中心波长标定法。

由拓扑图可知，每周期开始扫描时刻，驱动小板给采集卡一个触发信号，同时激光器按设定好的步进开始扫描，当监测到峰值时，用该时刻的索引乘步进加初始时刻波长即可计算出反射光的中心波长；再结合每个光栅的相关系数，即可计算出待测量，上位机解调流程图如图2 所示。

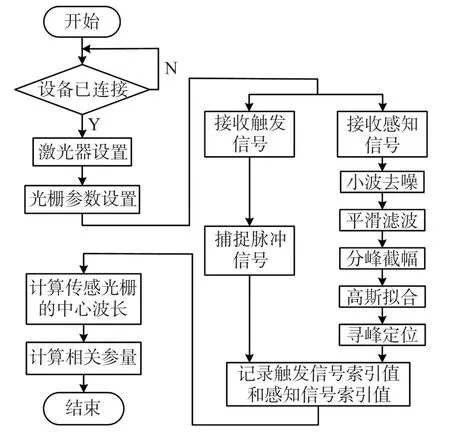
图2 上位机解调流程图

由上述解调原理可知，反射光的中心波长定位精确度，对整个监测系统的监测性能起着决定性的作用。而光纤光栅的工作环境中，经常有许多天然的或者人为的信号，诸如语音、地震波、生物信号等非平稳信号，加之光栅制造工艺、光路、电路的影响等，信号中夹杂着很多噪声，所以一种合适的寻峰算法对系统的精确度提升至关重要。图3 所示是当监测系统采用2 Hz 的扫描频率，接四个光栅时采集到的原始信号图，观察图可知，目标峰周围有较多杂峰、信号图中有很多毛刺，且目标峰周围有可能会伴随有假峰。

图3 原始信号图

2.2 小波去噪

因为反射信号中经常混杂有非平稳信号，给有效信号的解调带来不利的影响，本文采用小波变换法进行降噪。与傅里叶变换采用无限长的三角基作为基函数不同，小波变换采用的基函数是一定长度的逐渐衰减的小波基，表达式如(5)所示

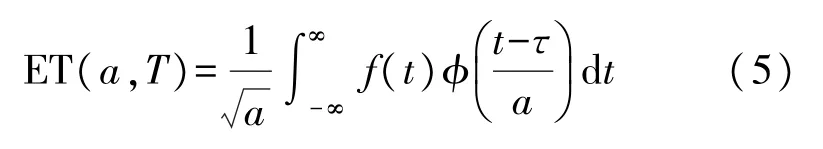
式中，a代表函数的伸缩量，τ代表函数的平移量，a与频率成反比，τ对应时间。小波去噪时，需要选择合适的阈值函数，常用的阈值函数有硬阈值与软阈值函数，表达式如(6)和式(7)所示[16]:

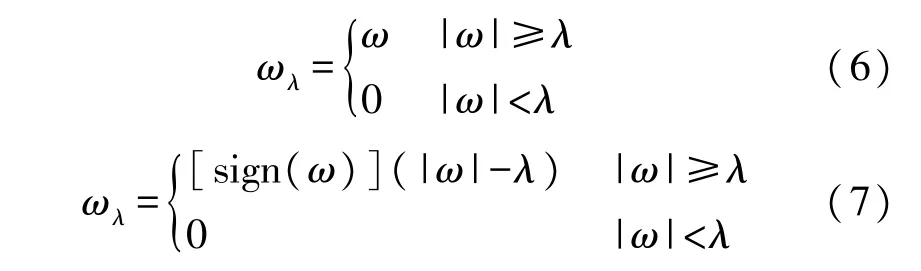
由函数表达式可知，硬阈值法在临界点附近会发生跳变，所以去噪以后的信号会发生震荡，故信号平滑性不如软阈值法，但是去噪重构之后的信号更逼近原始信号。为兼顾信号的平滑性与准确性，本文采取改进的阈值法，即把小波信号分解为七层，对1～3 层信号进行硬阈值处理，对4～7 层的信号进行软阈值处理，再将信号进行重构；本系统选用Coiflet(coifN)小波，其中参数N根据信噪比SNR 和均方根误差RMSE 进行选择，不同参数对应的数据如表1 所示，观察N选不同参数时三组数据可知，当N＝4 时信噪比SNR 最大、均方根误差RMSE 最小，所以选择coif4 作为小波基。各层信号及处理后的波形图如图4、图5 所示。

图4 小波分解信号

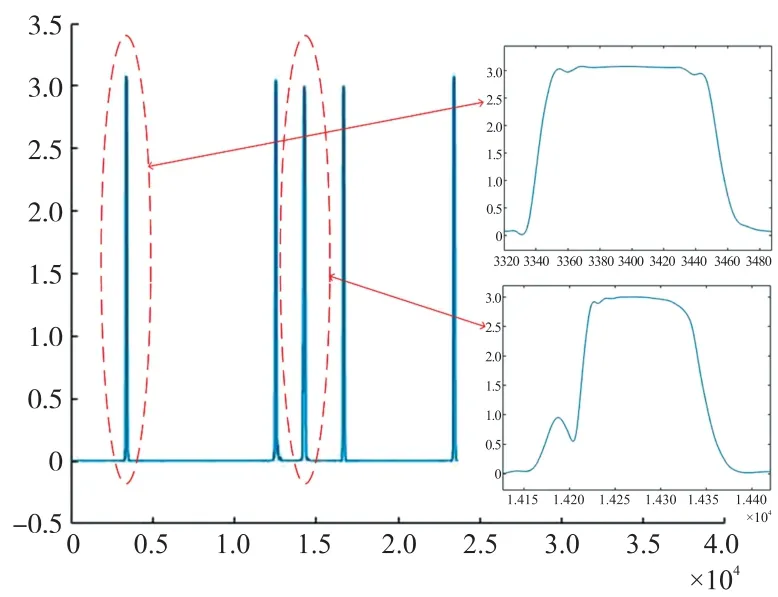
图5 小波去噪后信号图

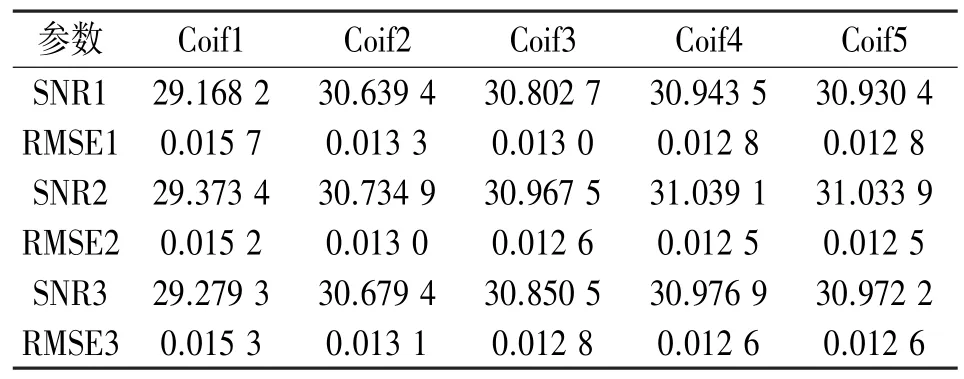
表1 小波相关参数对比表

2.3 滑动平均滤波

通过小波分解、去噪、重构之后的信号，在平滑性方面得到了极大提升，但是由图5 可知，信号中的假峰仍然存在，为消除信号中假峰的影响，方便下一步准确寻峰，本文采用滑动平均算法，处理之后的波形图如图6 所示。

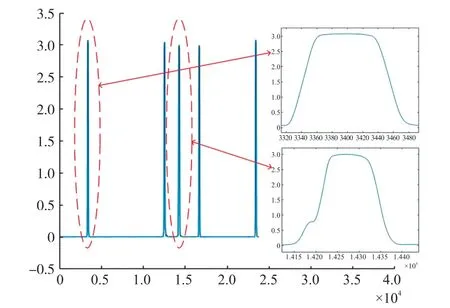
图6 滑动平均滤波后信号图

2.4 高斯拟合寻峰

经过小波去噪、滑动平均滤波，假峰基本消除，但是仍然做不到准确定位，以上述扫描频率2 Hz、采样率40 000 的信号为例，在峰值附近有约100 个采样点，换算成波长约为0.204 nm，误差范围太大，鉴于反射波形是彼此不重叠的单峰且去噪之后的波形除峰顶之外大致符合高斯分布，所以本文先用分峰截幅截取各反射峰，然后再对各峰进行高斯拟合，为了尽可能保持原数据特征，将截取波峰的幅值设置在0.05，波峰截取及拟合寻峰图形如图7、图8 所示。

图7 波峰截取

图8 高斯拟合后信号图

3 实验结果分析

测量的精确度是指测量数据和真实值的分布情况，是对测量值精密度和准确度的综合考量。测量的精确度越高，表明监测系统的稳定性和准确性越高。图9 是本系统进行数据采集和解析的系统实物图，系统所使用的光源为1 528 nm～1 568 nm、线宽小于5 MHz，步进为1 GHz、扫描频率为2 Hz 的循环扫描激光器，采集卡的采样率设置为40 kSa/s。

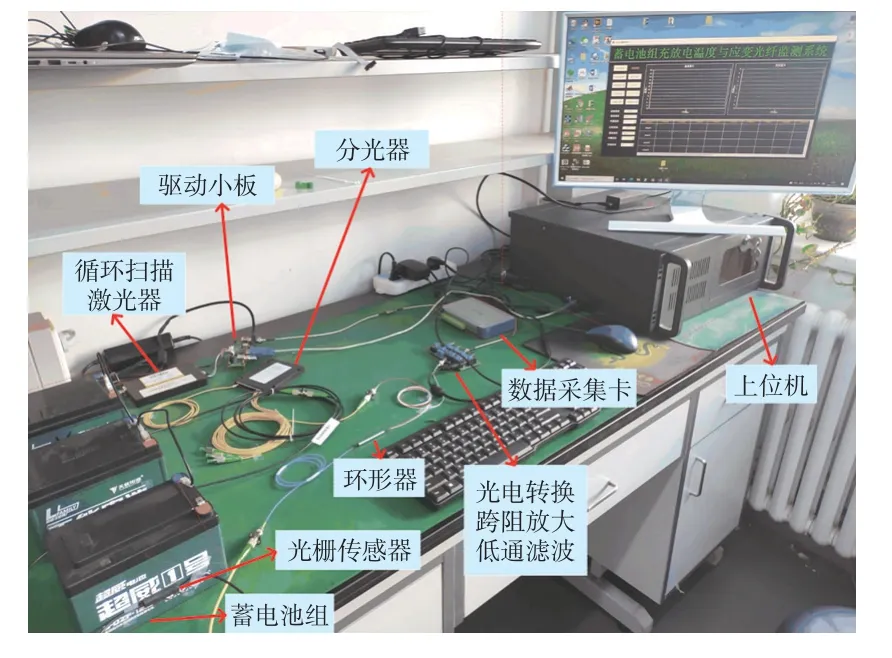
图9 系统实物图

3.1 温度测量精确度分析

实验分别采用中心波长为1 534.792 nm 和1 553.190 nm的温度光栅进行系统准确性分析，各项参数如表2 所示。

表2 光栅参数表

将光栅1 和光栅2 置于恒温箱中，分别将恒温箱设置在25 ℃～65 ℃，相邻两次测量温差为5 ℃，根据公式计算可得，在9 个温度下光栅的中心波长理论值如表3 所示。

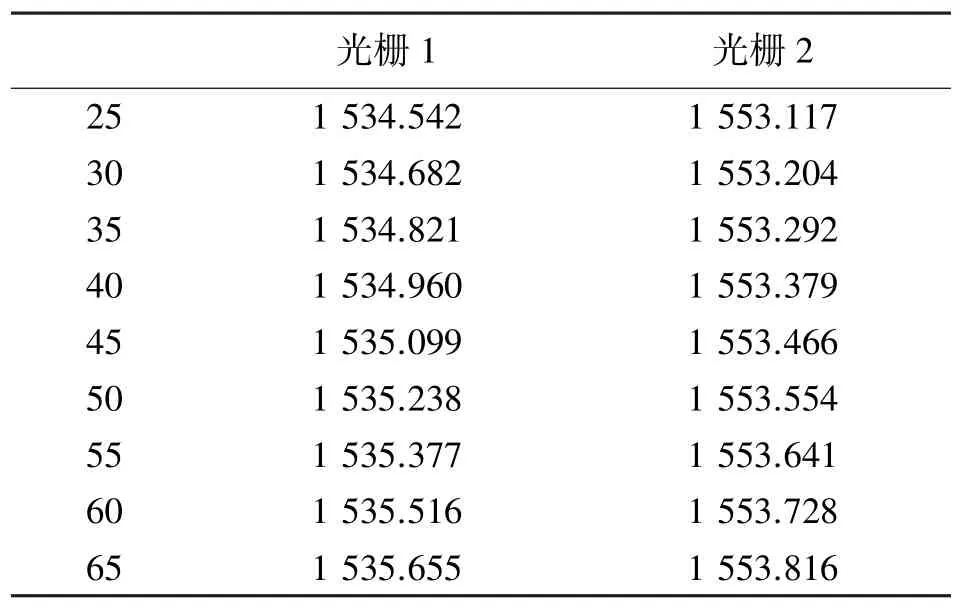
表3 光栅理论波长表

每次待恒温箱温度稳定后进行波长解调，分别对两个光栅在9 个温度下进行7 组重复试验，循环多次实验，记录数值并绘制折线图如图10、图11所示。

图10 光栅1 测温实验数据折线图

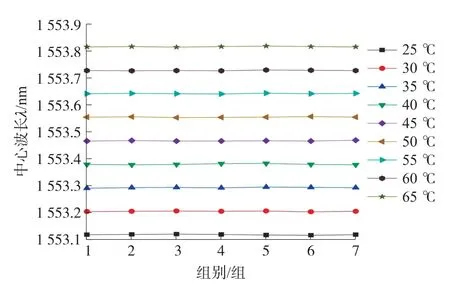
图11 光栅2 测温实验数据折线图

比较可得，系统测量误差均在±2 pm 之内，换算成温度分别为±0.072 ℃和±0.115 ℃，系统精确度较高。

3.2 应变测量精确度分析

进行应变光栅准确度分析时，系统采用中心波长为1 558.887 nm(25 ℃)、应变系数为456.954 2 με/nm、线性度为0.999 965 的裸栅，为更准确分析系统测量应变的准确度，实验过程中保持系统温度不变，以排除温度对波长的影响。将裸栅固定到平移台上，分别在0.03 mm、0.06 mm、0.09 mm 下进行波长解调，计算可得，实验所用光栅在25 ℃条件下理论波长分别为1 559.544 nm、1 560.2 nm、1 560.857 nm，每次待光栅恢复后再进行下一位移长度的波长解调，循环测量，记录数据并绘制折线图如图12 所示。

观察图12 可知，系统测量误差在±3 pm 之内，换算成应变为±1.37 με，系统精确度较高。

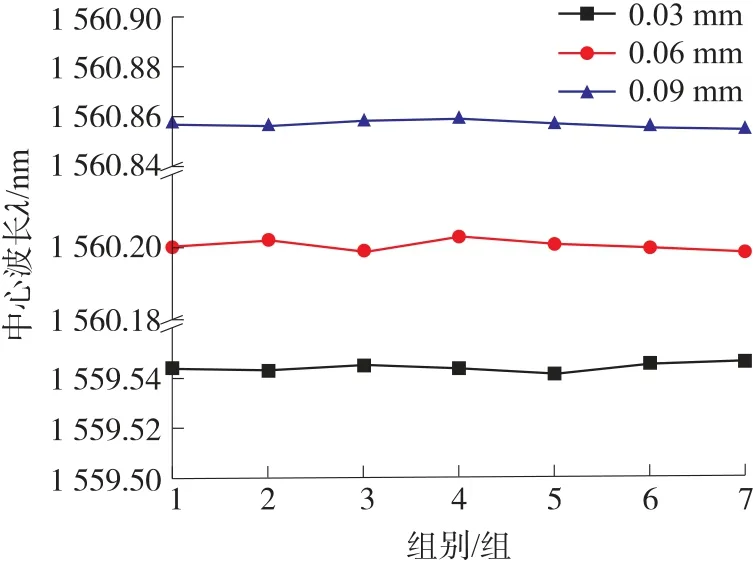
图12 光栅测应变实验数据折线图

4 结束语

针对蓄电池组充放电过程中个别电池异常发热、外壳鼓包、变形、胀裂等潜在的火灾隐患问题，根据光纤光栅的温度敏感和应变敏感特性设计了基于光纤光栅传感的循环扫描式蓄电池组充放电温度与应变监测系统，并提出一种融合改进小波去噪、滑动平均及高斯拟合算法的优化寻峰算法来提高系统的测量精度。该方法根据SNR 和RMSE 参数选取Coif4 小波基对反射的信号进行小波去噪处理，然后通过滑动平均算法提升信号平滑性，最后使用高斯拟合算法在尽可能保持原始信号数据特征前提下将峰值定位到单点，提高了系统的定位精度。经实验验证，该方法可以将温度测量精度控制在±0.12 ℃以内，应变测量精度控制在±1.37 με 以内，综上，本文提出的方案适用于蓄电池充放电过程中的温度与应变监测。