一种基于磁传感器定位技术的滑坡监测方法

卢鸿飞，高迪驹，张松勇，渐开旺

(上海海事大学航运技术与控制工程交通运输行业重点实验室，上海 201306)

滑坡作为一种常见的地质灾害，具有极大的危害性。每年我国因滑坡产生的直接经济损失就高达数百亿元。因此，如何对滑坡进行有效监测便成为了灾害防范极为重要的课题。

滑坡监测方法依据监测对象可以分为位移、物理场、地下水、外部诱发因素四个大类[1]。其中，位移是滑坡变形过程中的重要监测对象[2]。位移监测可分为地表位移监测和深部位移监测两类。地表位移监测技术有全球定位系统[3]、干涉雷达(InSAR)[4]等，该类方法具有良好的精度和时效性，缺点是只能反映滑坡表面的变形情况，无法获得滑坡深层的变形信息。深部位移监测采用的主要技术是钻孔测斜[5]，通过加速度传感器和磁传感器得到的数据解算出测点的姿态信息，进而可获得滑坡深层的变形曲线。

磁传感器是把磁场、电流等外部因素引起的磁性能变化转为电信号，并通过这种方式检测物理量的器件。磁传感器有着高灵敏度、高频、低功耗等优势，被广泛地应用在国防、医疗、勘探等领域。根据磁传感器所测量的磁感应强度变化，可以分析出测点的姿态和位置信息，因此磁传感器在滑坡监测方面具备一定的定位功能。目前，磁传感器在滑坡监测的研究主要集中在两个方面:

一是滑坡深层大位移的监测，大位移监测以磁定位技术为基础，根据磁感应强度值求解滑坡的直线位移。大位移监测的另一种思路是通过梯度法实现目标物的空间定位，如潜艇定位，但该方法应用到滑坡上时有成本高、安装难度大等问题，目前缺乏相关的研究。文献[6]为解决滑坡监测孔因剪短而失效的问题，推导了滑坡深部位移和磁感应强度的理论关系，提出了一维磁定位技术，但该方法只能监测滑坡的直线位移，且未考虑到地磁变化磁场的影响。文献[7]在该方法的基础上，采用差分布置方案来消除地磁和环境磁场的影响，缺点是需要确定滑坡倾角，并只能监测滑坡直线位移。这两种方法在实际工程中都难以应用。

二是滑坡深层小位移的监测，这方面的代表技术是钻孔测斜，目前国内外的研究主要集中在钻孔测斜的误差校正和缺点改良。文献[8]阐述了钻孔测斜及其滑坡应用的基本原理，提出了一种钻孔量测数据的处理方法和深度修正的计算公式。文献[9]分析了钻孔测斜的各项误差，提出了基于地磁场的方位角校正方法，对铁磁钻具引起的干扰磁场进行了误差校正。文献[10]研制了一种基于霍尔元件传感器的新型测斜仪，用于监测边坡位移，并进行了标定、验证和斜坡模型试验验证其可靠性。文献[11]针对钻孔适用性差、测量局部倾角困难等问题，开发了基于MEMS 的无线钻孔测磁系统，并验证了该系统的有效性。钻孔测斜法需要用到加速度传感器和磁传感器，同时使用两类传感器不仅加大了安装难度、增加了成本，还扩大了误差。

因此，本文提出一种基于磁传感器的精简测斜方式，以钻孔测斜法为基础，通过对地磁场数据进行处理和分析，实现对滑坡体深部位移的监测。磁传感器根据测得的磁感应强度解算出测点的姿态信息，即方位角、倾角和工具面角。

1 姿态测量

地磁场作为地球内部天然存在的物理量，可以近似为偶极子[12]。地磁场由稳定磁场和变化磁场[13]组成，在测量地磁场时，变化磁场会影响到测量结果，其中磁静日的影响约为10 nT～40 nT[14]。变化磁场引起的误差相对于地磁场较小，在精度要求不高的情况下可以将其忽略。

在目标山体上打下钻孔，将磁传感器布置于钻孔中，当滑坡发生时，钻孔在滑体的压力下会产生形变，如图1 所示。固定在钻孔中的磁传感器也会随着钻孔的形变发生旋转或移动。当形变较小时，可以认为磁传感器围绕中心点发生了旋转。当形变较大时，钻孔会被直接剪断。

图1 钻孔变形示意图

地磁场作为一个矢量场，在不考虑地磁时变影响时，它在一个位置的合成矢量不变。磁传感器发生旋转后，测得的新三分量磁场相当于原三分量磁场在新坐标系下的对应大小。因此，磁传感器的姿态测量可以用旋转变换来表示，利用欧拉定理，建立如下坐标体系。

初始钻孔坐标系OXYZ(即初次在钻孔中安装磁传感器的坐标轴) 以及变形后钻孔坐标系OX2Y2Z2(当滑体发生移动，磁传感器发生旋转后，得到的坐标轴)，两个坐标系之间的变换能通过有限次转动表示。初始钻孔坐标系OXYZ经过三次旋转变换可以到变形后钻孔坐标系OX2Y2Z2。初始坐标系OXYZ先围绕Z轴旋转α角，得到OX1Y1Z坐标系，OX1Y1Z坐标系再围绕X1轴旋转β角，得到OX1Y2Z1坐标系。OX1Y2Z1坐标系再围绕Y2轴旋转γ角，得到OX2Y2Z2坐标系。

以传感器初始位置为基准，三次旋转的角度α，β，γ分别为方位角，倾角和工具面角。需要说明的是，这三个角度并不直接对应钻孔测斜中的三个姿态角。即三个姿态角不以北西天或东北天坐标系为基准，而是以磁传感器初始位置为基准建立的。取值范围上，与钻孔测斜的定义[15]相同。以逆时针方向为正，方位角α取值范围为0°～360°，倾角β取值范围为-90°～90°，工具面角γ取值范围为0°～360°。坐标系旋转变换示意图如图2 所示。

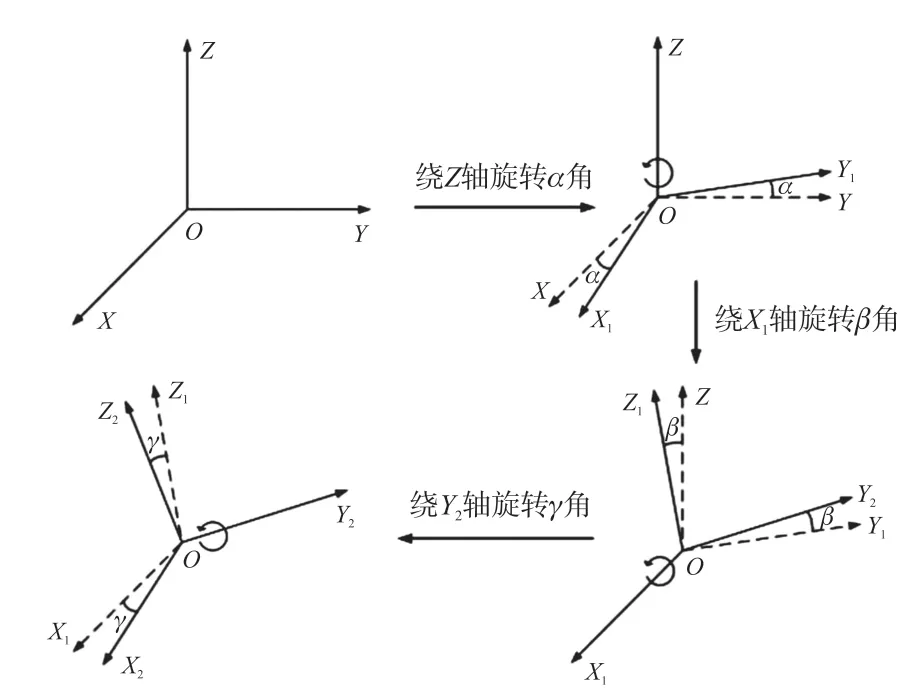
图2 坐标系旋转变换示意图

根据图2，可以得到如下的数学关系式。

式中:X2，Y2，Z2为变形后的磁感应强度三分量值，X，Y，Z为初始的磁感应强度三分量值。

两个坐标系之间的变换矩阵R为:

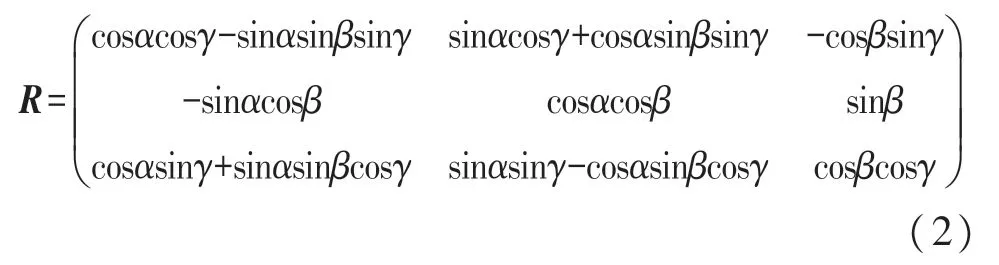
当磁传感器随着钻孔变形而旋转后，可以得到初始的磁感应强度三分量和变形后的磁感应强度三分量。式(1)为非线性方程，有三个未知数α，β，γ，无法求得精确解。传统测斜方法会根据加速度传感器和磁传感器的测值联列得到姿态角，但需同时用到两个传感器。为了降低成本，减小施工难度，可通过牛顿迭代法[16]求解方程的近似根。

牛顿迭代法通过函数的泰勒级数来作函数的切线，得到根的近似值。通过多次迭代，不断逼近根的真值。在求解上述方程的过程中，迭代次数是一个关键的参数。迭代次数越高，求解的精度会越高，同时也会增加解算的时间。

由于非线性方程不存在求根公式，在求解近似解的时候会存在多解的情况，可以通过提供合适的方程初始解来处理该问题。磁传感器安装入钻孔后，可以得到初始的钻孔坐标系。此时三个姿态角α，β，γ都为0°，将三个姿态角设置为方程初始解。由于滑坡变形是一个缓慢的过程[17]，通常需要数个月或数年，对应的磁传感器姿态角变化也是个缓慢的过程。在连续对姿态角进行采样时，姿态角的变化曲线近似于连续函数，在没有磁场干扰时，不会突然出现大幅度变化(即离散函数)的情况。由于姿态角的曲线近似于连续函数，每次根据新测量的三分量磁感应强度得到的磁传感器姿态角即为实际解。所以，每当磁传感器姿态角发生变化后，将新得到的姿态角设置为初始解，再在新的初始解附近寻找方程的根。

2 滑坡位移测量

得到磁传感器的姿态角信息后，可以计算滑坡位移。滑坡位移监测的主要对象是水平位移，所以水平位移计算公式为

式中:d为磁传感器的长度，L为水平位移，β为通过磁传感器测量得到的倾角。

从式(3)中可以看出位移的一种特殊情况，即磁传感器沿着坐标轴发生了平移，此时β＝0°，式(3)便不再适用。考虑到滑坡的受力体系比较复杂，不同部位、不同深度的受力存在明显的区别[18]，因此该情况较少，在滑坡小位移的情况下基本可以忽略。

根据上述步骤，滑坡水平位移求解流程图如图3所示。

图3 位移求解流程图

3 实验

实际工程中为了更准确地反映滑坡不同深度的位移情况，会在钻孔的不同深度安装磁传感器，用以监测不同测点的滑坡位移情况。因此搭建一套由两个磁传感器组成的测磁系统，来模拟滑坡不同深度的位移情况。磁传感器选用TAM-A 三分量磁通门传感器，其测量范围为[-2×105nT，2×105nT]，分辨率为1 nT。磁传感器已进行了初步的正交误差校正。将两个磁传感器连接到18 通道测磁电路板上，电路板通过网线与计算机连接，使用上位机软件将传感器测量到的数值实时传送给计算机。测磁系统框图如图4 所示。

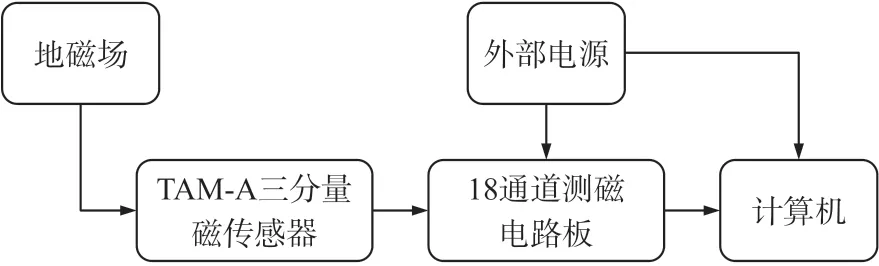
图4 测磁系统框图

由于滑坡变形的过程十分缓慢，将磁传感器的采样频率设置为2 Hz。将两个磁传感器固定在铝棒的两端(一个传感器正向放置，另一个反向放置，相当于两个传感器一个轴测值不变，另外两个轴测值相反，即两个磁传感器对应的方位角和倾角互为相反数，工具面角同号)，再将铝棒固定在无磁转台上，轴的最小刻度都为1°。实验场地选在磁场干扰少的室外环境，在地面上安置无磁转台的基座，固定后测得当地的地磁场B＝4.847 5×10-5T。实验布测环境如图5 所示，位于上侧的磁传感器统称为传感器1，位于下侧的磁传感器统称为传感器2。将传感器1 视为测点1，传感器2 视为测点2，通过实验比较不同测点处传感器的姿态角α，β，γ和水平位移L。

图5 实验布测环境

首先单独对三个姿态角α，β，γ依次进行误差实验。方位角α通过旋转Z轴来调整，从0°～360°每隔1°测量一次，循环测量五次，根据两个磁传感器解算方位角的平均误差和标准差，绘制两个磁传感器方位角α的部分误差线，如图6 所示。图中横坐标为方位角α，纵坐标代表平均误差。以平均误差为中点，竖线长度的一半为标准差。

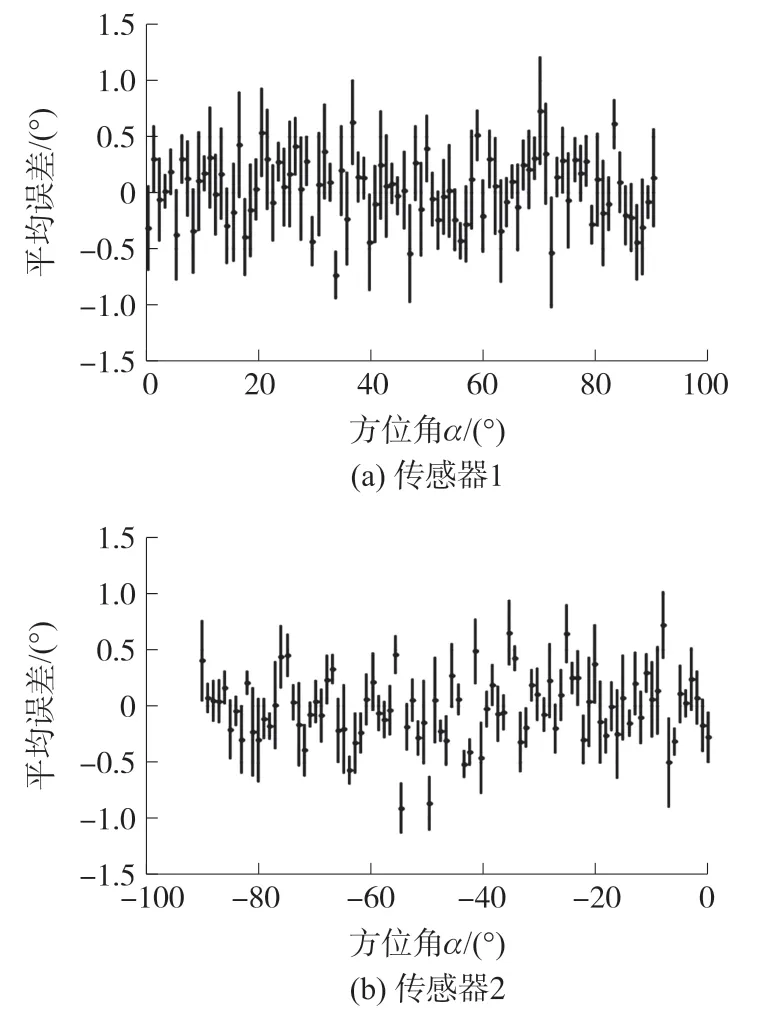
图6 方位角α 误差线

倾角β通过旋转X轴来调整，从-90°～90°每隔1°测量一次，循环测量五次，根据解算倾角的平均误差和标准差，绘制两个磁传感器倾角β的部分误差线，如图7 所示。

图7 倾角β 误差线

工具面角γ通过旋转Y轴来调整，从0°～360°每隔1°测量一次，循环测量五次，根据解算工具面角的平均值和标准差，绘制两个磁传感器工具面角γ的部分误差线，如图8 所示。

图8 工具面角γ 误差线

对两个磁传感器的实验数据进行统计，得到三个姿态角的平均绝对误差和最大误差如表1 所示。

目前通常使用的测斜仪器倾角测量误差为±0.2°，方位角测量误差为±1.5°[15]。由表1 得到三个姿态角的平均误差都在1°以内，可以满足实际测量的需要。

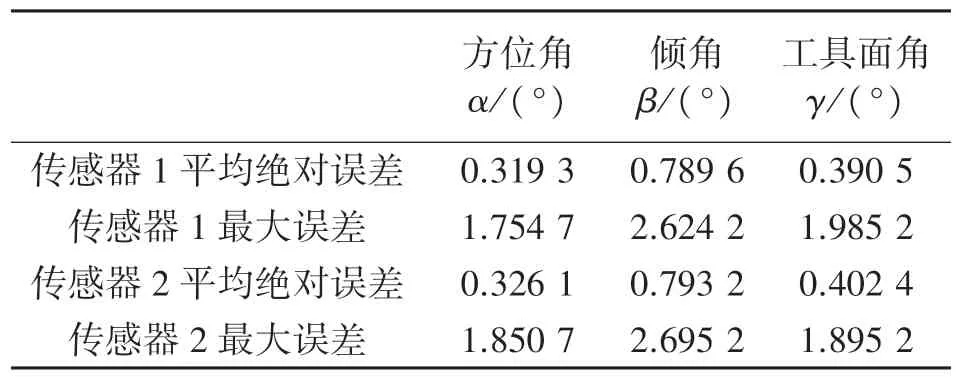
表1 姿态角误差表

为了进一步验证该方法的有效性，不再对单独的姿态角进行测试，对三个姿态角都进行调整。由于实际滑坡的位移曲线会发生波动，表现出一定的振荡特性[2]，姿态角的调整也以振荡的方式进行，故设计如下的姿态角变化过程。以初始磁传感器坐标系为基准，逆时针方向，三个姿态角一开始都为0°，方位角α，倾角β，工具面角γ按照(0°，0°，0°)到(20°，10°，5°)到(0°，20°，20°)到(15°，50°，20°)到(25°，25°，0°)到(50°，50°，10°)的顺序依次在无磁转台上缓慢旋转磁传感器，每旋转1°短暂停留2 s。通过上位机实时采集磁传感器测得的三分量磁感应强度，将保存的数据通过牛顿迭代法进行解算，从而得到姿态角的运算解，再将每次的运算解赋值给下次运算的初始解，从而实现姿态角的实时解算。将两个传感器的运算解与实际旋转角进行对比，可以绘制姿态角对比图像如图9 所示。

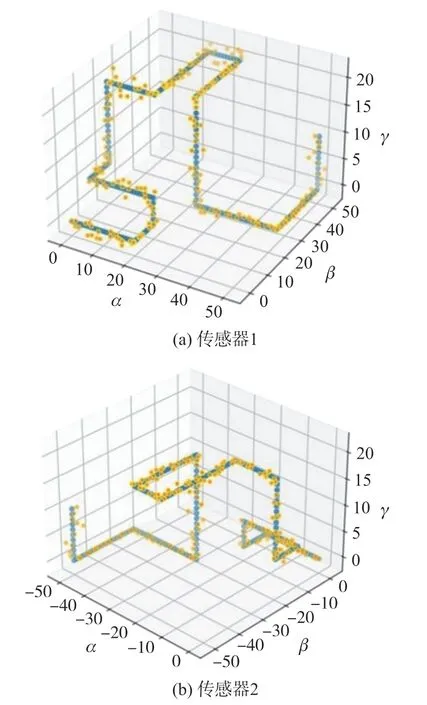
图9 旋转角对比图

图9 中，折线段为实际旋转角，散点为运算解。对实验数据进行统计，多角度变化情况下，三个姿态角的平均误差都在1°以内。总的来看，运算解的空间曲线与实际旋转角的空间曲线较为吻合，运算曲线的变化规律与实际情况基本一致。其中有个别异常点，可能是由于周边磁场干扰引起的，磁传感器测量不到准确的地磁场数值，影响了解算的精度。由于误差较小，该方法可用于解算磁传感器姿态角，由式(3)L＝dsinβ可以进一步得到滑坡深部的水平位移，从而保证水平位移的精度。

基于图9 得到了磁传感器倾角β的变化曲线，根据式(3)可以绘制出两个磁传感器水平位移的实际值和计算值如下。

磁传感器的长度为60 mm，由倾角的平均绝对误差可以得到磁传感器水平位移的平均绝对误差为0.867 mm，最大误差为2.847 mm。

由于两个磁传感器倾角互为相反数，根据式(3)可以得到两个磁传感器的水平位移也为相反数，从图10 中可以看出，不同传感器的实际位移和计算位移都很接近，解算的效果较好。

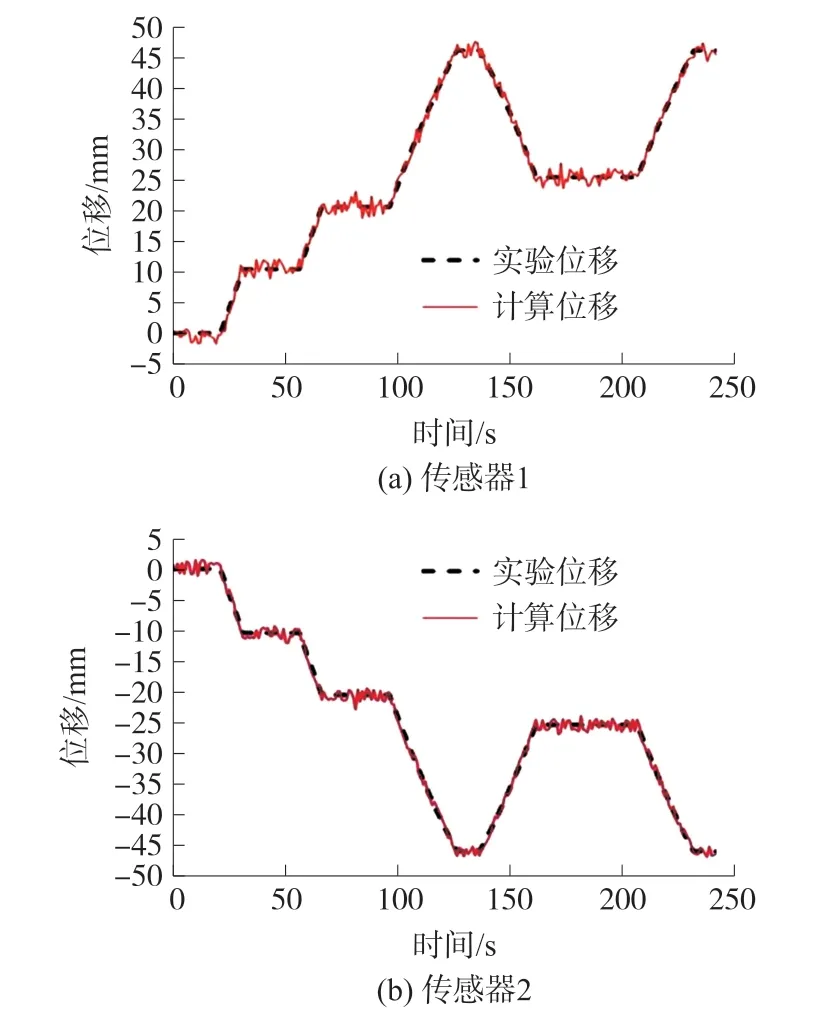
图10 位移对比图

4 误差分析

式(1)给出了姿态角的数学公式，并通过牛顿迭代法求得姿态角的近似解。理论上，通过控制精度得到的近似解应很接近实际的姿态角。但实验结果表明，两者之间存在一定的误差，该问题由以下几个方面导致:

①磁传感器系统误差。如零位误差、正交误差、温度漂移等。实验选用了磁通门传感器，它的探头结构存在一定的不对称，这会引起零位偏置，也会导致A/D 转换时零点不一致，发生零点偏移。正交误差是指磁传感器在安装过程中，需要保证三个磁轴两两垂直，但实际安装中存在一定的测量误差。温度漂移是由温度变化引起的误差，当环境温度变化时，电阻和电流也会变化，导致磁感应强度测量不准确。本次实验由于进行的时间较短，环境温度变化不大，在室外环境长时间运行时，必须将温漂误差考虑在内。

②铁磁材料干扰。当磁传感器周边存在铁磁材料时，会产生磁罗差，干扰磁传感器的测量。

③观测误差。无磁转台需要人手动进行转动，由于读数习惯和人为操作的原因，旋转时停留的角度存在一定的误差。

④地磁场时变干扰。地磁场会随时间发生变化，由于滑坡监测的周期很长，当地磁变化磁场扰动较大时，通过地磁场解算姿态角时会产生一定的误差。

5 结论

针对传统测斜存在的造价高、安装困难等问题，利用磁定位技术的高精度、自动化监测、实时性等优势，提出一种基于磁传感器的滑坡位移监测方法。该方法以磁传感器的姿态解算为基础，借助传感器采集的地磁场数据，通过牛顿迭代法实时解算传感器姿态信息，并将姿态信息转化为滑坡的水平位移。通过实验证实:①该基于磁传感器定位技术的监测方法三个姿态角平均误差在1°以内，最大误差在3°以内，水平位移平均误差小于1 毫米，最大误差小于3 mm，符合测试要求。②运用该方法进行滑坡位移监测无需加速度传感器，降低了成本，减小了施工难度。③基于磁传感器的滑坡位移监测方法可为实际工程应用提供有效的参考。