基于点阵行列变换的图像置乱算法
2022-02-04石玲玉吴雁南邹艳妮
石玲玉,吴雁南,周 铭,邹艳妮
(1.浙江广厦建设职业技术大学信息学院,浙江 金华 322100;2.南昌医学院,江西 南昌 330004;3.南昌大学数学与计算机学院,江西 南昌 330031)
随着计算机网络技术和通信技术的发展,图像传输的信息安全问题被很多学者研究。目前,图像加密算法按加密思路主要分为以下几类:基于空间域的像素置乱、基于混沌的加密、基于变换域的加密、基于秘密分割与秘密共享的加密、基于神经网络和元胞自动机的加密、基于盲源分离的加密[1]。基于空间域的置乱变换,有Arnold变换及其扩展变换、幻方变换、魔方变换等,用这些变换置乱图像,一般需要迭代若干次,而且有周期性[2-7]。文献[8]采取分数傅里叶变换和小波分解对彩色图像分级加密,克服了基于空间域的置乱变换的周期性,但算法比较复杂。文献[9]提出了基于素数的图像置乱技术,用双密钥(P,M)对图像进行加密,实现算法和密钥分离,提高了置乱图像的安全性,但其置乱效果依赖于密钥M的选取。针对这些不足,本文设计了一种基于点阵行列变换的图像置乱算法,利用变换:f(x)=x*(M+k) modP(其中k是点阵的行号或列号),对图像点阵逐行逐列置乱。由于该算法中的每行每列的变换都不相同,彻底打乱了像素点的空间位置,使得原图像的像素点在置乱图像中的排列杂乱无章。
1 置乱原理
定理1设P是素数,集合N={1,2,…,P-1},M∈N,则映射
f(x)=x*MmodP,x∈N
(1)
是N上的一一映射。
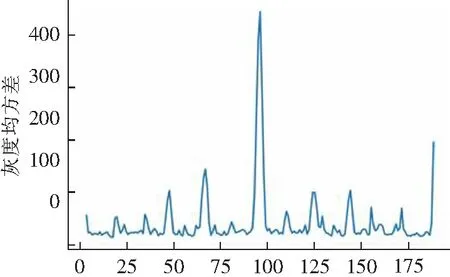
证明显然0≤f(x)≤P-1。假设f(x)=0,则存在非负整数k,值得x*M-k*p=0,即x*M=k*p,因为P是素数,所以P整除x或P整除M,但x 另一方面,如果有x1≠x2(不妨设x1>x2),使得f(x1)=f(x2),则存在非负整数k1与k2,值得x1*M-k1*p=x2*M-k2*P,即(x1-x2)*M=(k1-k2)*P,所以P整除(x1-x2)或P整除M,但0<(x1-x2) 综上述,f(x)是N上的一一映射。 定理1表明,f(1),f(2),…,f(P-1)是1,2,…,P-1的一个排列。对于小于P的自然数s,删除排列f(1),f(2),…,f(P-1)中大于s的整数,保持其他数的顺序不变,就得到1,2,…,s的一个排列:t1,t2,…,ts。文献[9]将图像的点阵转换成一维数组(b1,b2,…,bs),把数组元素下标按t1,t2,…,ts重新排列,再将重排的一维转换为二维点阵,这样就得到置乱图像。 选用经典测试用例Lena图像,大小256*256,如图1所示。用文献[9]的置乱算法,取素数p=521,当m=3时的置乱图像如图2所示。由此看出,如果M选取不合适,置乱图像呈现分块状。所以M不能随意选取,要想找出效果好的置乱图像,M需要遍历2,3,…,P-1,所以该算法效率很低。 图1 Lena原图Fig.1 Lena original image 图2 lena置乱图像Fig.2 lena scrambling image 下面简单分析一下置乱图像呈现分块状的原因。对于1,2,…,36组成的二维数组(如图3所示),取p=37,m=2,作变换f(x)=2*xmod 37,x=1,2,…,36,变换后的数组如图4所示。由于取模运算的规律,图4就分成4块,每一小块都保留着原数组的“全息”。因为图像的像素点很多,作这样的变换后,每一小块都有原图像“完整”的像素点,只是像素点稀疏了,这样置乱图像就成块状。 图3 原数组Fig.3 Original array 图4 变换后的数组Fig.4 Transformed array 针对上述情况,下面设计的算法分别对点阵的每行每列作变换: f(x)=x*(M+k) modP,(x=1,2,…,P-1) (2) 其中k是行、列号,这样每行、每列的变换规律就不相同,从而完全打乱了原图像素点的分布,达到好的置乱效果。 设A=(aij)mn是原图像的像素点二维数组,B=(bij)mn是A置乱图像的像素点二维数组,C=(cij)mn是B还原图像的像素点二维数组。 不妨假设m≤n,任意选取一个比2n大的素数P,任取一个小于P-n的自然数M,P和M作为密钥保存。 先对行进行加密,即从第1行开始逐行置乱; 再对列进行加密,即从第1列开始逐列置乱。置乱算法流程如图5所示。 解密过程正好和加密过程相反,先对列进行还原,即从第n列开始逐列还原;再对行进行还原,即从第m行开始逐行还原。还原算法流程如图6所示。 图5 置乱算法流程图Fig.5 Flow chart of scrambling algorithm 图6 还原算法流程图Fig.6 Flow chart of reduction algorithm 仍选用经典测试用例Lena图像(图1),任取大于512的素数P=521和自然数M=3,对图1用本文的加密算法进行置乱,得到置乱图像如图7所示。 图7 本文算法置乱图像Fig.7 The algorithm scrambles images 为了评估本文算法的优劣,用随机数和Arnold变换对图1进行置乱,将其置乱图像与本文算法的置乱图像做比较。 (1)随机数的置乱 如果原图像的像素点在置乱图像中是随机均匀分布的,那是很理想的状态。因此可以用随机数产生的置乱图像作为衡量一个置乱算法优劣的标准。 利用随机函数,将图1的像素点随机变换位置,得到置乱图像如图8所示。 图8 随机数置乱图像Fig.8 Random numbers scramble the image (2) Arnold变换置乱 用Arnold变换[2]对图1进行置乱,2次迭代置乱图像如图9所示,20次迭代置乱图像如图10所示,50次迭代置乱图像如图11所示。 图9 2次迭代置乱图像Fig.9 Scrambles the image in sub-iteration 从视觉上看,本文算法产生的置乱图像比Arnold变换产生的置乱图像效果要好,与随机数产生的置乱图像效果相当。 用本文算法得到灰度图像的置乱图像,灰白像素点分布很均匀,丝毫看不出原图像的痕迹。那么对于彩色图像置乱效果怎样呢?我们选择色彩比较丰富的花卉图像(如图12所示),其置乱图像的彩色像素点分布也是非常均匀的,如图13所示。 图像置乱目的是使图像非法获得者,难以还原图像的本来面目,即不易猜中密钥,这就需要密钥敏感性非常高。 图12 花卉原图像Fig.12 Original image of flowers 取密钥p=521,m=4,对置乱图像(图7)进行还原,得到图像如图14所示。取密钥p=523,m=3,对置乱图像(图7)进行还原,得到图像如图15所示。可见算法对密钥非常敏感。实际上,如果密钥错误,则解密就相当于再次加密。 图13 花卉置乱图像Fig.13 Scrambled images of flowers 图14 错误密钥还原图像1Fig.14 Error key restores image 1 图15 错误密钥还原图像2Fig.15 Error key restores image 2 (1) 噪声影响 在置乱图像(图7)中加入30%的噪声,即随机把图像30%的像素点变为白色,如图16所示。 图16 加入噪声图像Fig.16 Add noise image 图16的还原图像如图17所示。 图17 噪声还原图像Fig.17 Noise reduction image (2)裁剪影响 在置乱图像(图7)中间裁剪掉面积30%正方形,即把图像裁剪的像素点变为白色,如图18所示。图16的还原图像如图19所示。 图18 中间裁剪图像(30%)Fig.18 Middle cropped image (30%) 在置乱图像(图7)四角裁剪掉面积30%正方形,即把图像裁剪的像素点变为白色,如图20所示。图20的还原图像如图21所示。 图19 中间裁剪还原图像(30%)Fig.19 Middle clipping restores image (30%) 图20 四角裁剪图像(30%)Fig.20 Quadrangle cropped image (30%) 图21 四角裁剪还原图像(30%)Fig.21 Cut corners to restore image (30%) 在置乱图像(图7)四边裁剪掉面积30%正方形,即把图像裁剪的像素点变为白色,如图22所示。图22的还原图像如图23所示。 由此可见,不论裁剪置乱图像哪个部分,原图像(图1)的主要信息和大部分细节在还原图像(图17,19,21,23)中还能保留。 噪声和裁剪实验表明,置乱图像抗干扰能力强。这也说明原图像的像素点在置乱图像中的分布是均匀的,置乱图像的任何部分都有原图的“全息”。 图22 四边裁剪图像(30%)Fig.22 Cropped image on four sides (30%) 图23 四边裁剪还原图像(30%)Fig.23 Restore image by clipping on four sides (30%) 对于置乱效果的定量描述,一般有两种方式。一种是基于距离的,即点(x,y)变换到(x′,y′)的距离d越大越好[10];另一种是基于灰度的,即点(x,y)的灰度与其周边点的灰度差越大越好[11]。笔者认为,应该从视觉上看,如果置乱图像整体灰度分布比较均匀,那么置乱效果就比较好。下面给出置乱效果的定量描述。 将图像点阵分成互补相交的子块,每块大小为s×t,令m′=m/s,n′=n/t,记每个子块为Bkl,(k=1,2,…,m′,l=1,2,…,n′)。 整个图像的灰度平均值: 每个子块Bkl,(k=1,2,…,m′,l=1,2,…,n′)的灰度平均值: 所有子块的灰度平均值与整个图像的灰度平均值的均方差: 很明显,均方差σ2越小表示每子块的灰度平均值就越接近整个图像的灰度平均值,置乱效果就越好。子块的大小要合适,不能过大过小,下面测试取8×8。 用Arnold变换对图1进行置乱,在第192次迭代出现周期。第1,2,189,190,191次迭代的灰度均方差分别是:1 307.57,683.04,619.2,1 142.6,1 629.35,为了能看出其他迭代次数灰度均方差的变换情况,去掉这几次特别大的。第3~188次迭代的灰度均方差对应的折线如图24所示。灰度均方差最小12.27,灰度均方差最大1629.35,波动很大。用Arnold变换置乱图像,需要在一个周期内迭代,才能找出置乱效果好的置乱图像。 迭代次数图24 Arnold变换置乱均方差Fig.24 Arnold transform scrambles mean square deviation 用随机数分别对图1进行200次置乱,置乱图像的灰度均方差都在30-40之间,如图25所示。 随机次数图25 随机数置乱均方差Fig.25 Random number scrambling mean square deviation 任取4个素数P=512,769,2 579,12 809,取M=1,2,…,200,用本文算法对图1进行置乱,分别计算置乱图像的灰度均方差,得到4条折线,如图26所示。所有灰度均方差都在30~40之间,波动很小,对应的置乱图像效果差异难以区分。因此图像的置乱效果与密钥(P,M)的选取无关。 对于彩色图像置乱效果的定量描述,可以根据式[12]:0.3R+0.59G+0.11B将(R,G,B)转变为灰度,再计算灰度均方差。 m取值图26 本文算法置乱均方差Fig.26 The algorithm scrambles the mean square error 基于点阵行列变换的图像置乱算法,置乱效果与密钥(P,M)的选取无关,表现出算法的鲁棒性。原图的像素点在置乱图像中分布均匀,任何子块都保留着原图的“全息”,因此抗干扰能力强,显示了算法的稳定性。同时置乱一次成功,无需多次迭代。另外,本文定义的灰度均方差来描述图像置乱效果,测试表明灰度均方差越小,置乱效果越好,这表明用灰度均方差来描述图像置乱效果是合理的。



2 加密与解密算法
2.1 加密算法
2.2 解密算法


3 实例测试



4 算法评价
4.1 密钥敏感性




4.2 抗干扰性





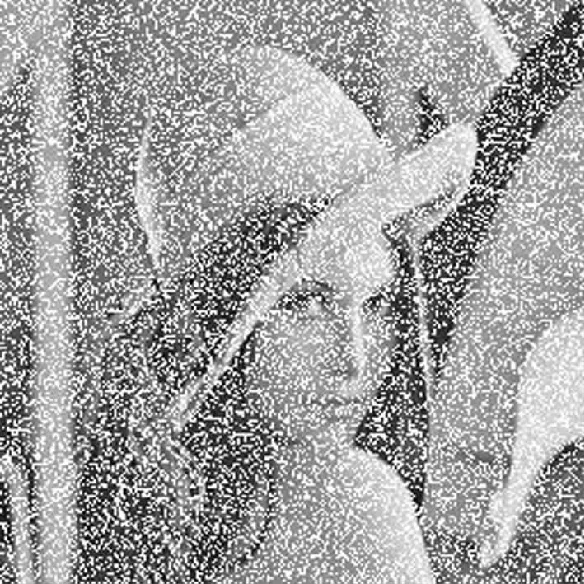


4.3 置乱效果定量描述

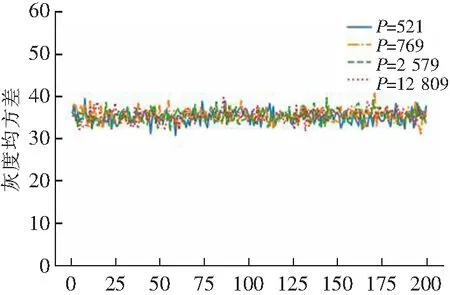
5 结论
