管内插螺旋液固两相流流场特征影响因素试验

彭德其, 付 翁, 冯 源, 俞天兰, 谭卓伟, 吴淑英, 王志奇

(1.湘潭大学机械工程学院, 湖南湘潭 411105； 2.湖南工业大学机械工程学院, 湖南株洲 412007)

换热管内插螺旋液固两相流具有结构紧凑、设备改造成本低、换热效率高等优点，广泛运用于化工、能源及冶金等工业领域[1-3]。然而，换热管内插螺旋液固两相流内部的流动特性复杂，多种因素会导致流体与管壁之间的换热规律异样多化[4-5]，使得换热管内插螺旋液固两相流工程设计较为复杂困难。国内外学者对换热器内插螺旋的流场及换热进行了相关研究。换热器内插螺旋相对于光管，其具有更好强化传热作用，Zhang等[6-9]研究表明, 加入内插螺旋使得管内流体产生额外涡流，呈现螺旋二次流，使流体在内壁上滑动，壁面附近的切向速度和径向速度得到提升，从而加速主流区域与近壁面区域之间混合，促进湍流动能，因此可更好达到强化换热效果。液固两相流中良好固相分布能更好强化传热传质，LÜ等[10-14]研究表明，液固两相流中固相分布涉及多种因素，包括表观液体速度、表观颗粒速度、颗粒密度、颗粒粒径、颗粒体积分数及颗粒形状等。然而液固两相流在实际工程应用中，大多数颗粒分布在圆管中心位置，导致换热效果不能达到最大化[15]。螺旋线圈使得管内流体呈螺旋流，径向速度增大产生离心力，引导颗粒碰撞壁面，破坏边界层，加剧湍流程度，能更好达到防除垢与强化换热效果[16-17]。但这些研究对内插螺旋换热管内液固两相流动行为分析不够充分，而流场与换热之间关系十分紧密[18]，因此研究管内液固两相流动行为对揭示流场影响传热具有重要意义。笔者通过自主搭建可视化内插螺旋液固两相流试验平台，采用PIV技术[19-20]，对立式管内插螺旋线圈进行试验研究，深入探究雷诺数、颗粒体积分数和颗粒粒径对管内流场特征影响。

1 试 验

1.1 试验装置

试验装置及粒子图像测速法(PIV)成像原理如图1所示，主要由PIV测试系统、水循环系统、试验测试段3部分组成。为捕捉管内充分发展段的流动情况，测试段采用长度L=1 000 mm、内径D=32 mm石英玻璃管。为减少水折射对图像质量影响，在管外安装一个60 mm×60 mm×800 mm矩形石英玻璃水槽。将示踪粒子(粒径小于10 μm)与水混合均匀后，加入密度为1.2 g/cm3的亚克力球形颗粒，由离心泵输送至试验循环系统中。为准确获取流体稳定运动状态，其测量部位距离圆管进口的90D处[20]。在激光给予能量情况下，利用CCD相机得到部件1的管中心纵截面图，通过软件计算以及采用tecplot后处理，得到涡量、径向速度、湍动能等物理量。

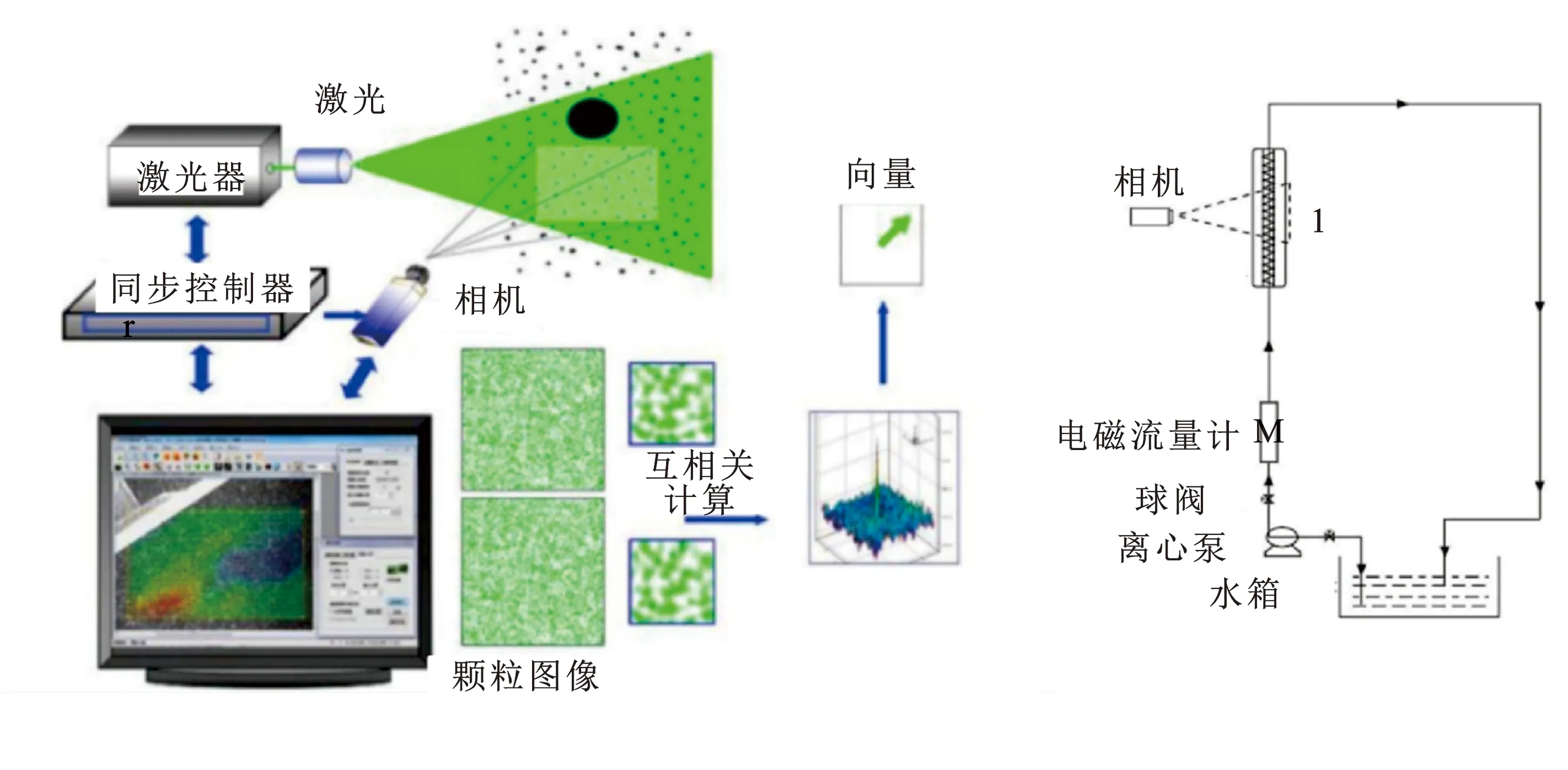
图1 试验装置及PIV成像原理Fig.1 Experimental setup and PIV imaging principle

1.2 试验材料及参数

自来水作为循环管路的介质。其颗粒材料为亚克力，密度为1.2 g/cm3，外径分别为1.5、2、3、4和5 mm，分别对应的沉降速度为0.094、0.109、0.134、0.154 9和0.174 m/s。其颗粒体积分数(φ=1%、2%、3%、4%、5%)是粒子总体积与(水+粒子) 总体积之比。

1.3 试验工况

采用彭德其等[16]所得的最优螺旋结构参数(丝径e=1.5 mm、螺距s=20 mm、外径D=30 mm)，在流速为1 m/s(Re=33 000)时螺旋将稳定运动，考虑颗粒Φ=5 mm，φ=5%时，颗粒流态初始化所需速度为0.8 m/s(Re=26 400)，因此Re选定为26 400、28 600、30 800和33 000。因螺旋与颗粒运动具有瞬时性，为增加数据的真实可靠性，每种工况下测量3组数据取平均值。为确定雷诺数Re、颗粒体积分数φ(1%、2%、3%、4%、5%)和颗粒粒径Φ(1.5、2、3、4、5 mm)三种因素对流场的影响，试验中控制两个变量分别研究Re、φ、Φ对流场影响。

1.4 参数定义

纵截面内涡量Ωxy定义为

(1)

式中，U和V分别为轴向速度和径向速度，m/s。

湍动能K[17]定义为

(2)

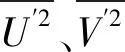
2 结果与讨论

壁面附近涡量影响边界层分布与传热，且涡量受到颗粒参数和流体速度影响。为探究边界层附近涡量规律，取Re=26 400，φ=1%，Φ=1.5 mm工况，由试验测得此时边界层厚度，该工况下边界层厚度为最大值0.2 mm，其余工况下边界层厚度在0.174 ～ 0.2 mm，因此取管壁附近2 mm(边界层厚度的10倍)的区域为研究对象(图2左侧线框)，通过分析得到近壁处局部涡量。

2.1 涡量分布规律

当φ和Φ分别为5%和1.5 mm时，不同Re下涡量如图2所示。整体涡量主要呈正负分布在螺旋与流体接触的管壁周围，说明流体存在旋流运动，增强了管壁区域(x/r=±1.0)流体扰动程度。图3是Re为33 000、Φ为1.5 mm工况下，不同体积分数涡量云图。由图3可以看出，涡量整体分布位置大致相似，主要集中分布在螺旋与管壁之间，涡量最大值随着颗粒体积分数增大而增大。而Re为33 000、φ为5%时，不同颗粒粒径下涡量云图分布如图4所示。涡量最大值随着Φ增大逐渐变小，且分布变得稀疏。三者对管内涡量的影响分布规律相似，涡量主要分布在螺旋与管壁之间，管中心位置(x/r=0)涡量较少。

对比图2、3、4和试验观察，可知：随Re增加，螺旋振动频率及流场扰动增大，导致旋流更加剧烈及沿半径运动范围变大；随着φ增加，或随着Φ减小，管内颗粒数目增多，导致颗粒与壁面、颗粒与颗粒、颗粒与螺旋的碰撞愈加频繁，使得流场内的颗粒旋转角速度变得更大，进而涡量值变大。

为了进一步量化3个运行参数对流场影响，分别计算在不同工况和截面上的平均涡量。图5为Re、φ、Φ对平均涡量的影响。由图5可知：在试验范围内，局部涡量与Re、φ呈正相关，但与Φ呈负相关。且Re对局部涡量分布影响因素最大，φ因素次之，最小影响因素为Φ。

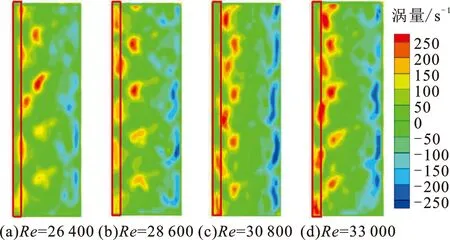
图2 不同雷诺数下的流体涡量云图Fig.2 Fluid vorticity cloud diagram under different Reynolds numbers

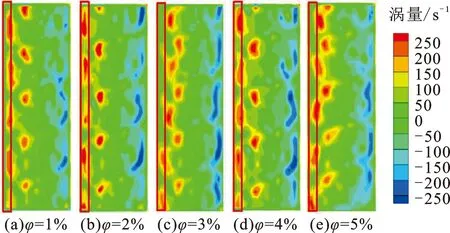
图3 不同颗粒体积分数流体涡量云图Fig.3 Fluid vorticity cloud diagram with different particle volume fractions

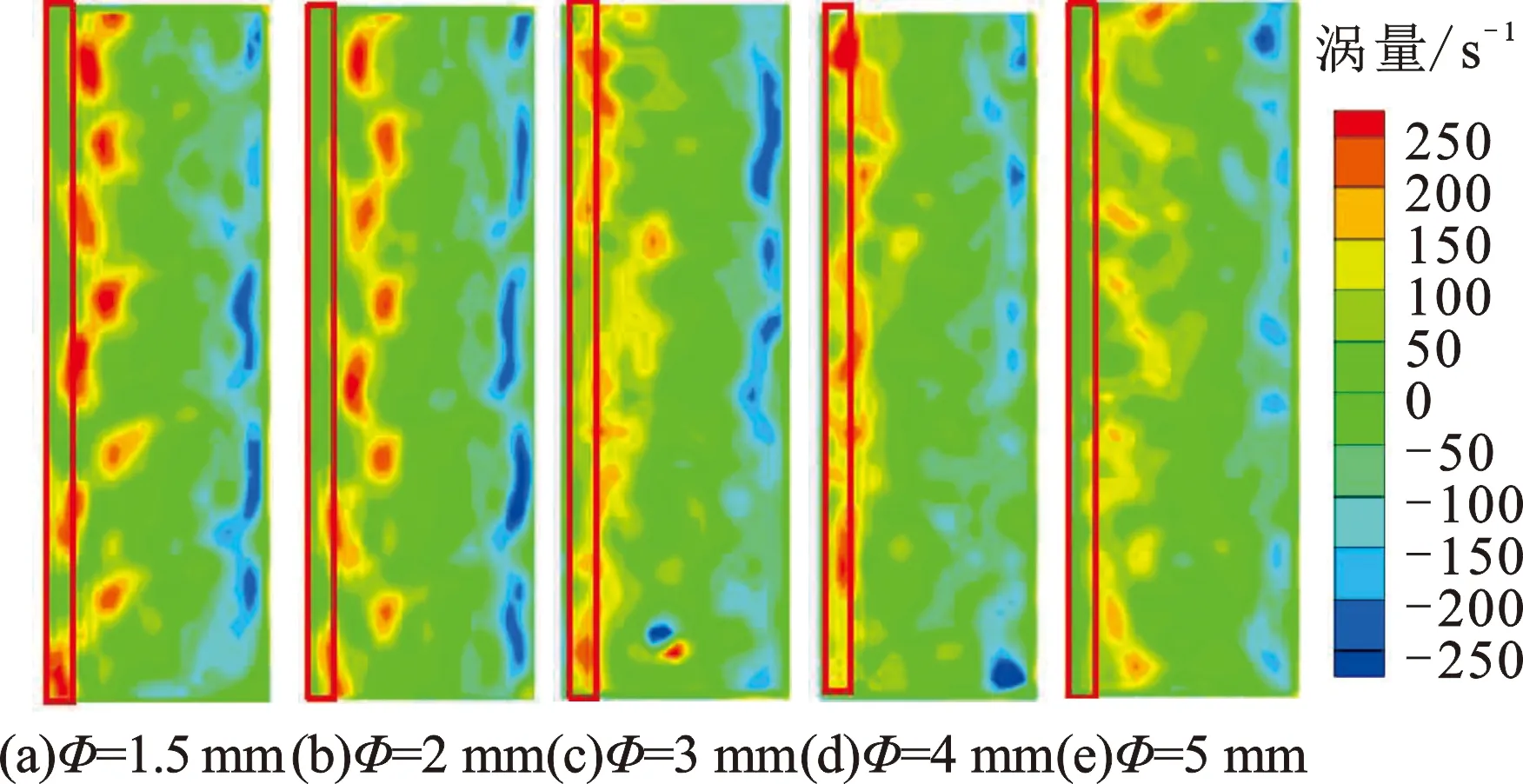
图4 不同颗粒粒径下流体涡量云图Fig.4 Fluid vorticity cloud diagram under different particle sizes

Re对平均涡量影响如图5(a)所示，在Re小于30 800时，平均涡量随着Re增加呈迅速增长趋势，但在Re大于30 800后，涡量增长变缓，渐渐趋于稳定。同时可以看到，局部涡量平均值随Re变化规律与整体涡量平均值趋于一致，且远大于整体涡量平均值。在Re=33 000时，局部涡量、整体涡量平均值分别为145.4和93.3 s-1，相较于整体涡量提高55.8%，螺旋与颗粒共同作用使得圆管管壁区域流体湍流更加强烈，这将促进换热。

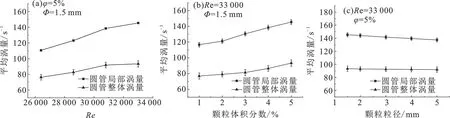
图5 雷诺数、颗粒体积分数、颗粒粒径对平均涡量的影响Fig.5 Influences of Reynolds number, particle volume fraction, and particle size on the average vorticity

由图5(b)可知：①对于整体涡量，体积分数为5%工况相比于体积分数为1%时平均涡量提升21.3%，说明随着φ增加，颗粒与流体之间的碰撞变得更加剧烈，加速了涡流形成;其中体积分数为3%～5%相较于体积分数为1%～3%时涡量大幅度提升；其主要原因是在管内空间一定时，管内颗粒体积分数越大，颗粒与壁面、颗粒与颗粒之间的碰撞几率会增加，在圆管内易形成湍流，使得管内平均涡量增大。②对于局部涡量，体积分数为5%工况相较于体积分数为1%下，其平均涡量增长了24.6%，局部涡量增长趋势与整体涡量相似，但是其增长幅度远大于整体涡量;主要原因是随着颗粒数目增多，颗粒在螺旋引导下，随流体运动中更多颗粒运动至管壁，颗粒与管壁碰撞加剧，颗粒易对管壁流体造成更强扰动，促进涡量形成，边界层被加剧削弱，这将更有利于流体换热。

由图5(c)可知：圆管整体涡量和局部涡量平均值皆随粒径增大而减小，二者变化趋势是相似的。对于整体涡量，相比于Φ=5 mm，Φ=1.5 mm的工况下整体涡量平均值提升了1.5%；对于局部涡量，Φ=1.5 mm其涡量平均值较Φ=5 mm增长了5.9%；且增长速率较圆管整体涡量平均值大4.4%，表明涡量主要集中于管壁附近，管中心涡量较少，与涡量云图的分布较为一致;其主要原因是在相同体积分数时，Φ=1.5 mm亚克力颗粒数目是Φ=5 mm的37倍，其流场中颗粒数更多，在管内分布更均匀及旋流引导下，更多颗粒运动至圆管内壁周围，加强颗粒与壁面之间的碰撞频率，减弱边界层附近的黏滞力，使得热量更便捷通过边界层(误差棒代表相应平均涡量标准差)。

2.2 径向速度规律

管内流体径向速度分布对于换热管传热效率有一定影响，径向速度越大，越有益于管中心与管壁流体之间的置换。

不同Re、φ、Φ下的径向速度均呈正负波动型分布，径向速度在管壁处相较于管中心位置明显大许多。由图6可知，随着Re、φ增大，径向速度峰值也逐渐增大，而颗粒粒径与之相反。

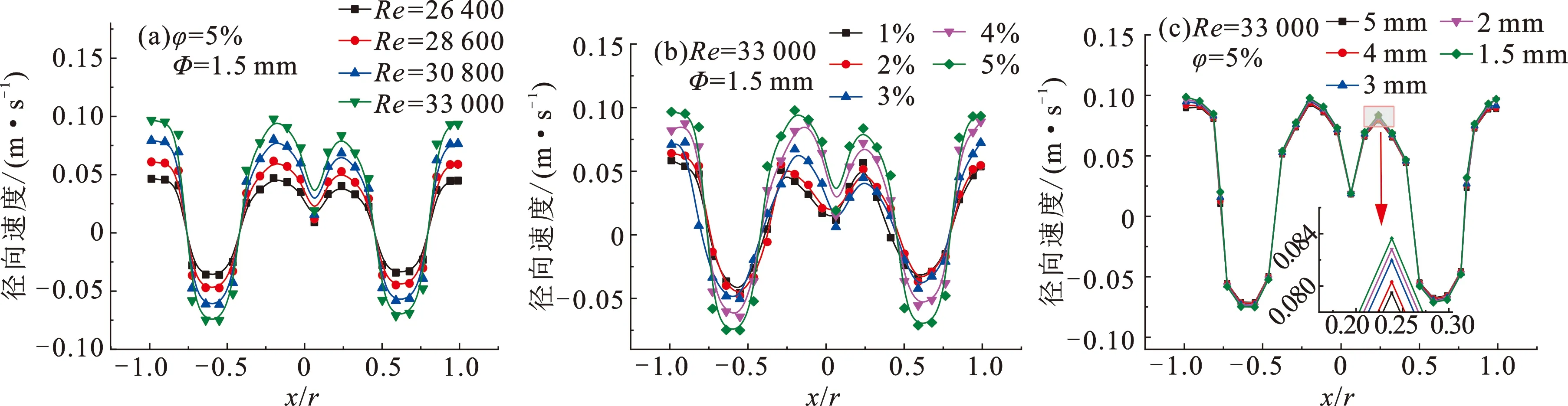
图6 雷诺数、颗粒体积分数、颗粒粒径对径向速度影响Fig.6 Influences of Reynolds number, particle volume fraction and particle size on radial velocity

由图6(a)可知，管内颗粒受到螺旋影响呈现为螺旋流运动，随Re增加流体离心力增大，径向速度增大。Re=33 000下最大径向速度为0.097 8 m/s，相较于Re=26 400提升108.5%。由于径向速度增大，增强了管内主流区与边界层之间流体交换频率，降低温度梯度，传热阻力减小。

由图6(b)可知，φ为5%时，其最大径向速度为0.097 m/s，相较于φ为1%时增长了67.24%。在管道体积一定情况下，φ越大，管内颗粒数越大，影响的流体区域更多，主流区域与管壁区域的流体混合和交换更为均匀，使得管内流体与管壁之间热量传递变得更加容易。

不同Φ下径向速度分布如图6(c)所示，径向速度峰值随颗粒粒径减小而增大。在相同体积分数下粒径越小，管内颗粒数量越大，因此在流场中颗粒与颗粒、螺旋、壁面之间相互碰撞几率增加，可提高流体径向交换程度。

2.3 湍动能分布规律

不同Re下湍动能分布如图7(a)所示，x/r=0表示管中心区域，x/r=±1.0为管壁区域，可知，Re越大，x/r=±1.0湍流程度越强烈，其边界层附近的流场愈加紊乱。在x/r=0处，不同Re下湍动能保持在一个稳定范围内，当Re越大，对于中心区域的湍动能，高雷诺数工况要略大于低雷诺数工况。

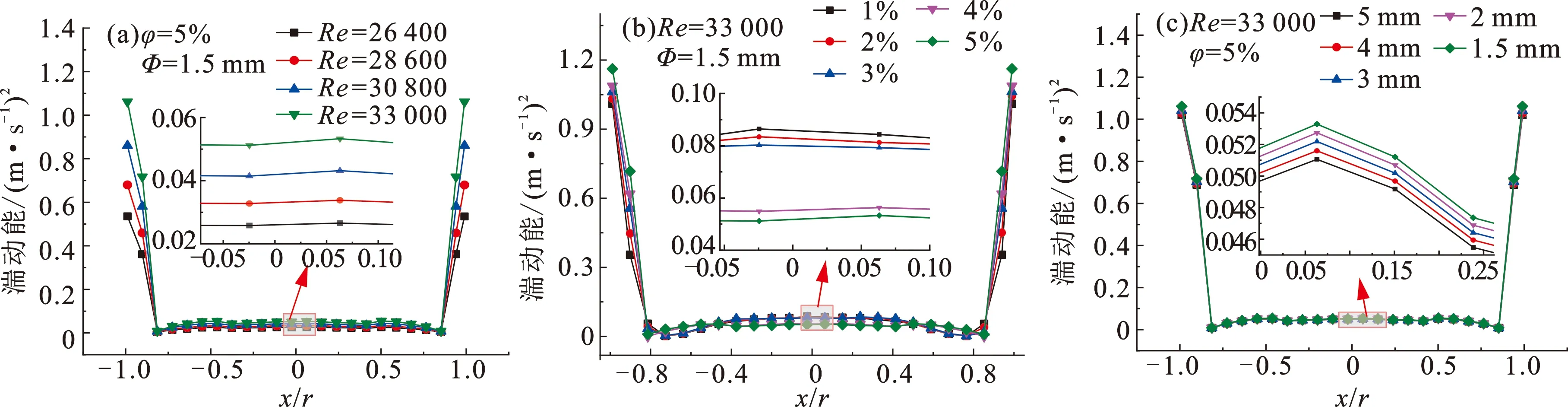
图7 雷诺数、颗粒体积分数、颗粒粒径对湍动能分布影响Fig.7 Influences of Reynolds number, particle volume fraction and particle size on distribution of turbulent kinetic energy

不同φ下湍动能分布如图7(b)所示。不同φ下的湍动能均在管壁区x/r=±1.0处具有最大湍动能，且管壁区域x/r=±1.0的湍流程度与颗粒体积分数呈正相关。颗粒体积分数越大，x/r=0区域流速会越小，高体积分数颗粒会导致中心区域流体的波动速度变小，因此低体积分数下的中心流域湍动能要略高于高体积分数工况。

不同Φ下湍动能分布如图7(c)所示。不同Φ湍动能均在管壁处具有最大湍动能，Φ越小，湍流程度越大；从x/r=-1.0壁面到近壁面x/r=-0.7区域湍流强度呈下降趋势，这是因为远离壁面区域，速度波动幅度变小。同时在管中心区域，对于粒径小的颗粒，其运动阻力越小，导致其速度越大，因此粒径小的工况其湍动能优于颗粒粒径大的工况。

由图7可知，湍动能最大值均在管壁与螺旋接触位置。在管中心位置，湍动能随着Re增大而增大，随着φ数和Φ增大而减小。

为进一步量化分析不同Re下湍动能，采用湍动能数值沿径向积分得到平均湍动能。在试验范围内，平均湍动能与Re呈正相关，Re为33 000平均湍动能相较于Re为26 400提升75.48%(图8(a))。说明Re越高，湍流强度越大，流体间的质点碰撞越激烈，导致管壁与流体之间能量交换越快，优化传热效果越好。

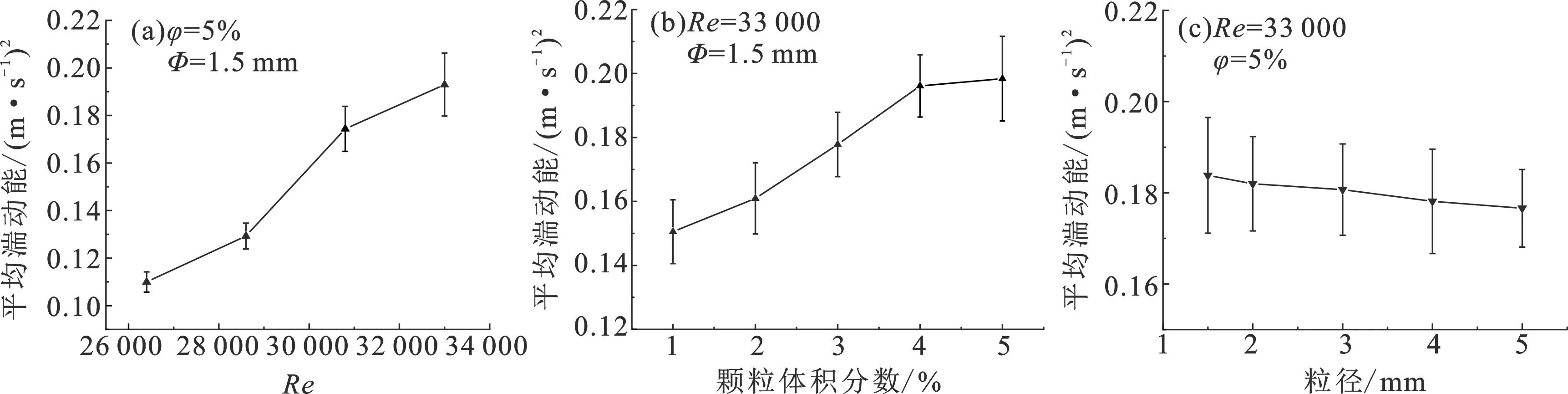
图8 雷诺数、颗粒体积分数、颗粒粒径对平均湍动能影响(误差棒代表平均湍动能标准差)Fig.8 Influences of Reynolds number, particle volume fraction, and particle size on the average turbulent kinetic energy (error bars representing standard deviation of mean turbulent kinetic energy)

平均湍动能随φ增大而增长，相比于φ为1%，φ为5%的平均湍动能提升16.7%，φ越大，颗粒越易破坏流动边界层，从而加剧湍流强度，有利于液固之间换热(图8(b))。但在增长幅度为4%～5%相较于增长幅度为1%～4%具有下降趋势，主要原因是随着φ增大，固体颗粒增多时可能阻碍流体流动，流体平均湍动能增长幅度下降。

如图8(c)所示，平均湍动能与Φ呈负相关，Φ为1.5 mm平均湍动能相比于Φ为5 mm提升9.83%，说明Φ越小，湍流强度越大。将管内流体充分混合，速度梯度变小，能有效减小流动边界层厚度，有利于热量传递。

由图8可知，其平均湍动能规律与湍动能分布规律相似。在管壁附近，皆与Re、φ呈正相关，与Φ呈负相关。

3 结 论

(1)整体涡量、近壁面区域平均涡量均与Re、φ呈正相关，但与Φ呈负相关；且近壁区域平均涡量比整体平均涡量增幅大，内插螺旋液固两相流可促进流体传热。

(2)在不同Re、φ和Φ下，径向速度均呈正负波动，径向速度峰值与Re、φ呈正相关，但与Φ呈负相关；提升径向速度，使主流区域与管壁区域的流体混合更为均匀，有利于热量传递。

(3)在试验范围内，Re为33 000比Re为26 400的平均湍动能提高81.7%，φ为5%比φ为1%的平均湍动能提高16.7%，Φ为1.5 mm比Φ为5 mm的平均湍动能提高9.83%。