瞬变电磁测井视电阻率提取方法及地质导向潜力
2022-02-03吴柏志袁习勇郭同政邓少贵
吴柏志,袁习勇,,郭同政,杨 震,鲁 超,邓少贵
(1.中国石化经纬有限公司,山东青岛 266075; 2.中国石油大学(华东)深层油气重点实验室,山东青岛 266580)
瞬变电磁法(transient electromagnetic method, TEM)测量信号源关断期间的纯二次场,测量过程不受一次场干扰,而且与时谐电磁场测量相比,包含了宽频域的丰富信息,在航空、近地表、隧道、矿井等领域应用广泛[1-3]。关于其在地球物理测井领域中的潜力,目前的理论探索主要集中在两方面:一是在生产井中,利用瞬变电磁场低频成分可以穿透套管进入地层的特性,研究其在过套管电阻率评价中的能力[4-6];二是利用瞬变电磁法探测距离远的特点,研究其在随钻地质导向远探测方面的应用[7-8]。近年来,国外油服公司申请了一系列瞬变电磁应用于地质导向的专利,内容涉及发射接收线圈系结构,激励源选取,以及随钻仪器金属钻铤影响的消除方法等[9-11]。当前时谐源激励的超深随钻电磁波测井探测深度可达数十米,但源距也有数十米;与之相比,瞬变电磁测井的重要优势在于探测深度受源距影响非常小[12-15]。作为电测井方法中最重要的地层参数,视电阻率在含油气地层评价中至关重要[16-20]。瞬变电磁法测量信号为感应电动势,一般通过电阻率转换算法将其转换为时域视电阻率。晚期视电阻率曲线在测量早期往往偏离真实情况,有时甚至不能反映地层的基本结构变化;为此,回线源激励的半空间、全空间领域已经发展出了解决该问题的全区视电阻率解释方法[21-22]。与之相比,石油测井探测尺度小得多,对测量前中期对应的近井视电阻率评价要求更高。针对随钻测井中常见的水平层状模型,笔者采用Gaver-Stehfest逆拉普拉斯变换与正余弦变换的数值滤波算法相结合的频-时转换混合算法,实现层状地层瞬变电磁测井响应的快速计算;提出适用于瞬变电磁测井的晚期视电阻率公式和全区视电阻率反演方法,得到层状地层的时域视电阻率曲线;基于全空间“烟圈”原理,模拟电场在地层中的扩散并分析电阻率的响应机制。
1 瞬变电磁测井正演及时域视电阻率提取理论
时谐电磁波测井和瞬变电磁测井都采用线圈作为发射接收天线,当源距远大于线圈尺寸时发射线圈可视为磁偶极子源,不同之处在于时谐电磁波测井的发射源为固定频率的交流电,而瞬变电磁测井采用脉冲源,通过测量脉冲源关断后感应涡流的时域扩散反映地层电性特征。对于可快速获得频域解析解的地层模型,一般采用频-时转换法计算瞬变电磁响应。
假设水平层状介质任意方向时谐磁偶极子源激励的频域磁场和电场分别为H(ω)和E(ω),具体过程许多文献[23-24]已有说明,在此不做详细推导。当瞬变电磁测井激励源为下阶跃脉冲源时,其响应可由直流响应与上阶跃电流响应作差得到[25],以磁场为例:
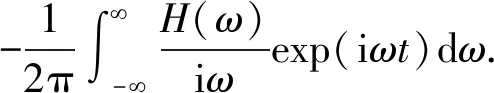
(1)
式中,第1项为直流响应;第2项为上阶跃响应。
首先利用正余弦变换的数值滤波算法求解时域磁场H(t),将式(1)积分函数中的指数项展开,并根据频域磁场H(ω)的实偶虚奇函数特性ReH(ω)=ReH(-ω),ImH(ω)=-ImH(-ω),得到H(t)的两种表达形式:
(2)
(3)
(4)
(5)
式中,N为线圈匝数;S为线圈面积;μ为地层磁导率。由此可见,频域磁场的实部或虚部皆可单独用来计算时域磁场。
根据贝塞尔函数与三角函数之间的关系:
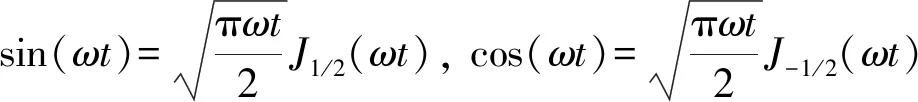
(6)
将式(4)和(5)中关于高振荡函数的积分转化为含±1/2阶贝塞尔函数积分的形式:
(7)
(8)
基于汉克尔变换理论,给出一种贝塞尔函数积分通式:
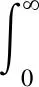
(9)
式中,Jv为v阶贝塞尔函数,v>-1。
式(9)的汉克尔变换离散求和表达式:
(10)
相应地,结合式(9)和(10),得到式(7)和(8)的汉克尔滤波形式:
csin(nΔ),
(11)
ccos(nΔ).
(12)
其中
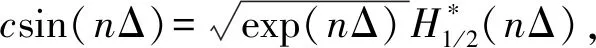
Δ=ln10/20.
式中,csin(nΔ)和ccos(nΔ)分别为正余弦变换的滤波系数; Δ为采样间隔。
与前文所述的正余弦变换数值滤波算法相比,G-S (Gaver-Stehfest)算法具有所需滤波系数少,计算速度较快,纯实数运算等优点;但是整体精度不如数值滤波算法[26]。G-S算法基于逆拉普拉斯变换,
(13)
其中s=-iω。根据G-S理论,f(t)的数值变换式为
(14)
其中
式中,J为G-S算法的滤波系数数目,由计算机的字长决定;Kj为滤波系数;m为(j+1)/2的整数部分。
由此得到G-S算法求解时域磁场H(t)和感应电动势V(t)的数值离散形式:
(15)
(16)
本文中正余弦变换的滤波系数分别为250点和401点,G-S算法的滤波系数分别取12点和14点。图1中地层电阻率为1 Ω·m,发射接收线圈同轴布置,源距为101.6 cm,比较正余弦变换和G-S计算结果得出:401点正余弦变换的精度远高于250点的精度,一般情况下,相同点数的正弦变换精度高于余弦变换;除了特别晚期外,14点的G-S算法精度高于12点。整体而言,G-S算法虽然精度不如正余弦变换,但所用滤波系数要少的多,因此速度方面快了数十倍。
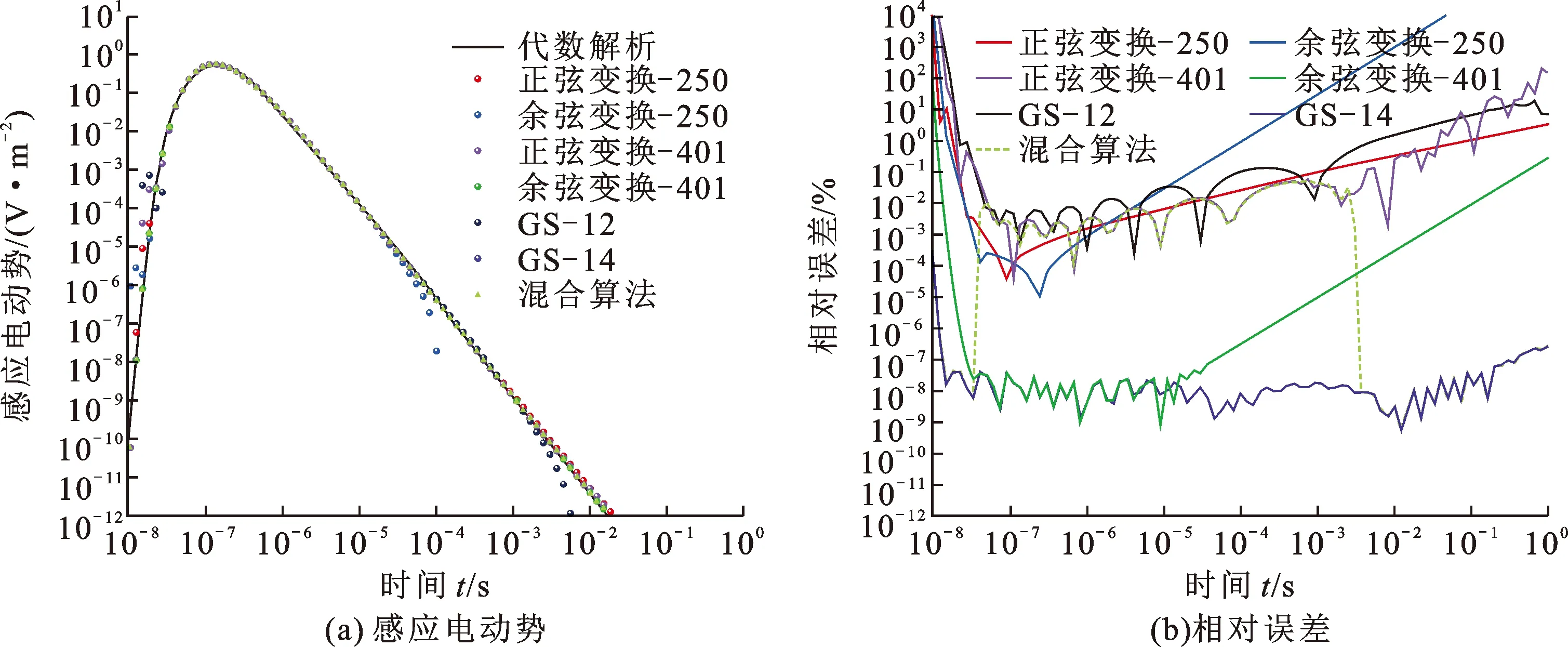
图1 不同频-时转换算法计算结果比较Fig.1 Result comparisons between different frequency-time conversion algorithms
综合两种频-时转换算法的优劣,制定本文中所用的混合算法方案如下:先用14点G-S算法计算所有时间采样点的响应,然后用401点的正弦变换滤波算法计算初始和最后时间采样点的值,并与G-S算法的结果比较。如果二者偏差较大,则将感应电动势更新为正弦变换的结果,紧接着由两端时间采样点向中间时刻推进,直到到达满足误差精度的时间采样点停止正弦变换对G-S结果的更新。混合算法集合了G-S和正弦变换算法二者的优势,在满足计算精度的同时大幅提升了计算效率。
将混合算法用于层状地层瞬变电磁响应正演,得到的感应电动势数据需要经过进一步处理才能从中提取地层视电阻率,本文的处理方法有晚期视电阻率公式和全区视电阻率反演两种。
首先以均匀地层为例提出瞬变电磁测井晚期视电阻率的定义,均匀地层感应电动势为
(17)
其中
m=IS,θ=(μσ/4t)1/2.
式中,m为磁矩;I为通电电流;σ为地层电导率。因为
(18)
测量晚期时间t取值较大时,式(17)可以简化为
(19)
此时定义瞬变电磁测井的晚期视电阻率Rl:
(20)
接下来讨论瞬变电磁测井的全区视电阻率反演方法,令φ=θL,将式(17)改写为
(21)
其中
Y(φ)=φ3exp(-φ2).
构建反演目标函数:
(22)
采用Halley反演方法[27],确定迭代步长:
(23)
当目标函数达到所需精度时停止参数的更新,此时全区视电阻率Ra为
Ra=μL2/4φ2t.
(24)
2 晚期和全区视电阻率的提取
采用晚期视电阻率公式和全区电阻率反演处理混合算法的感应电动势正演结果,得到不同地层模型随时间变化的晚期和全区视电阻率曲线。
2.1 均匀地层
以均匀地层为例,如图2(a)所示,晚期视电阻率曲线中只有当时间t增大到满足公式(20)的成立条件,视电阻率才与地层真电阻率(Rt)相等。涡流场在高阻层的扩散速度更快,比在低阻层更快满足晚期条件,所以随着地层电阻率的增大,视电阻率等于真电阻率的时间提前。全区视电阻率反演则很好地解决了以上早期结果的误差问题,经反演以后,任意时刻都能获得准确的地层电阻率。
图2(b)给出了源距(L)对视电阻率曲线的影响,源距为零表示发射线圈电流关断以后转变为接收线圈的情况,随着源距的增大,晚期视电阻率曲线等于地层真电阻率的时间延后;但是全区视电阻率曲线中源距变化不再影响视电阻率的提取结果。
2.2 两层模型
对于层状介质,首先考虑最简单的两层模型(图3,R和T分别表示接收线圈和发射线圈),源距为101.6 cm,改变仪器中心到边界的垂直距离(d)。
图4为仪器与界面垂直的时域视电阻率曲线,其中黑色虚线代表与仪器当前层电阻率相同的均匀地层。从晚期视电阻率曲线可以看出,由于测量早期感应涡流处于当前层,不同颜色的视电阻率曲线重合;当涡流向远处扩散遇到地层界面,曲线与黑色虚线发生分离,分离时间取决于d,并逐渐向邻层电阻率过渡:如果是高阻探低阻的两层模型,时域衰减后期渐近值大约为1.7 Ω·m,接近邻层电阻率真值;但是低阻探高阻时测量晚期视电阻率仅为1.7 Ω·m,远小于邻层电阻率,将这种由于近井低阻体的影响导致难以探测远井地层的现象称为“低阻屏蔽”。
时域早、晚期测量信号分别反映了近、远井的地层结构,晚期视电阻率公式得到的结果在早期时刻严重偏离真实值;全区视电阻率的优势在于经过反演以后的测量早期视电阻率与当前层真实电阻率相等。同时比较晚期和全区视电阻率曲线发现,经过全区视电阻率反演后虽能准确判断当前层电阻率,但缺乏邻层电阻率的确定能力:全区视电阻率曲线上对应的视电阻率,与相同时刻由晚期视电阻率公式得到的结果基本一致。观察全区视电阻率反演的目标函数发现,反演模型实际属于单层模型,只有电阻率一个待定参数,测量早期的感应电磁场集中在仪器所在层,所以选取单层反演模型足够且合理。但是中后期的电磁场在两个层都有分布,感应电动势受两层介质的共同影响:高阻探低阻时的主要贡献来自低阻邻层,中后期依然可以选择单层反演模型,并能得到基本反映邻层真电阻率的视电阻率;但是当低阻探高阻时,低阻屏蔽的原因导致时域衰减后期测量信号的主要贡献还是主要来自当前层,所以此时反演得到的视电阻率仍然主要反映当前低阻层的电阻率。
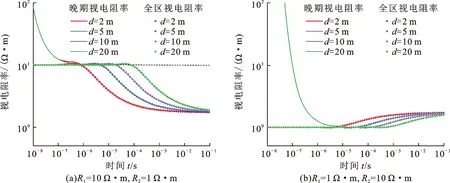
图4 直井两层模型不同d的晚期和全区视电阻率Fig.4 Late-time and all-time apparent resistivity of 2-layer model with different d in vertical well
当仪器与界面平行时,与直井相比,较为显著的变化发生在低阻探高阻的情况,如图5(b)所示,水平井的后期渐近值略有抬升,大约为2.6 Ω·m,但与邻层真实电阻率仍然相差较大。
2.3 三层模型
对于三层模型(图6),源距为101.6 cm,中间层电阻率R2=1 Ω·m,两侧围岩电阻率R1=R3=10 Ω·m,仪器位于中间层的中心位置,层厚H2是d的两倍,通过改变H2来改变d,为了与两层模型比较,此处令H2分别为4、10、20、40 m。
比较图7与图4(b)、5(b),两层模型与三层模型的响应有明显差异:低阻探高阻的两层模型曾出现低阻屏蔽现象,但当仪器两侧都有高阻围岩时,晚期的曲线渐近值约为10 Ω·m,与围岩真实电阻率相等;且水平井与直井相比,视电阻率变化速度更快。也就是说,当两侧有高阻围岩时,即使仪器位于低阻层,也不会受到低阻屏蔽的影响。此时经全区视电阻率反演后,早晚期结果准确反映了当前层和邻层电阻率。
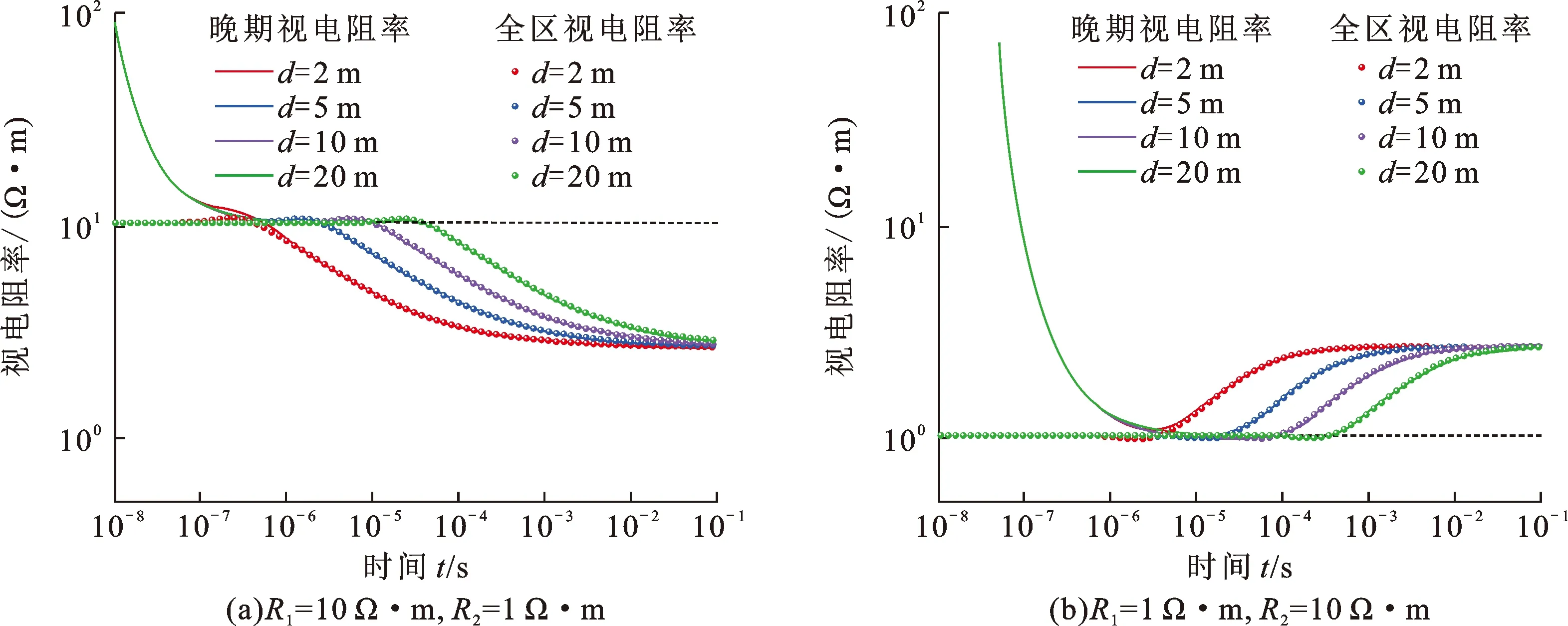
图5 水平井两层模型不同d的晚期和全区视电阻率Fig.5 Late-time and all-time apparent resistivity of 2-layer model with different d in horizontal well
以上考虑的是仪器位于中间层中心位置的情况,到两个界面的距离相等,如果仪器在中间层的位置发生变化,如图8所示,仪器与界面平行,到界面1和界面2的距离分别为d1和d2。图9和图10分别表示中间层为高阻和低阻的视电阻率响应,其中-3 m表示向下移动3 m,此时d1=2 m,d2=8 m,+3 m表示向上移动3 m,此时d1=8 m,d2=2 m。为对比说明,同时增加了H2分别等于4和10 m,但仪器位于中间层中心位置的算例。
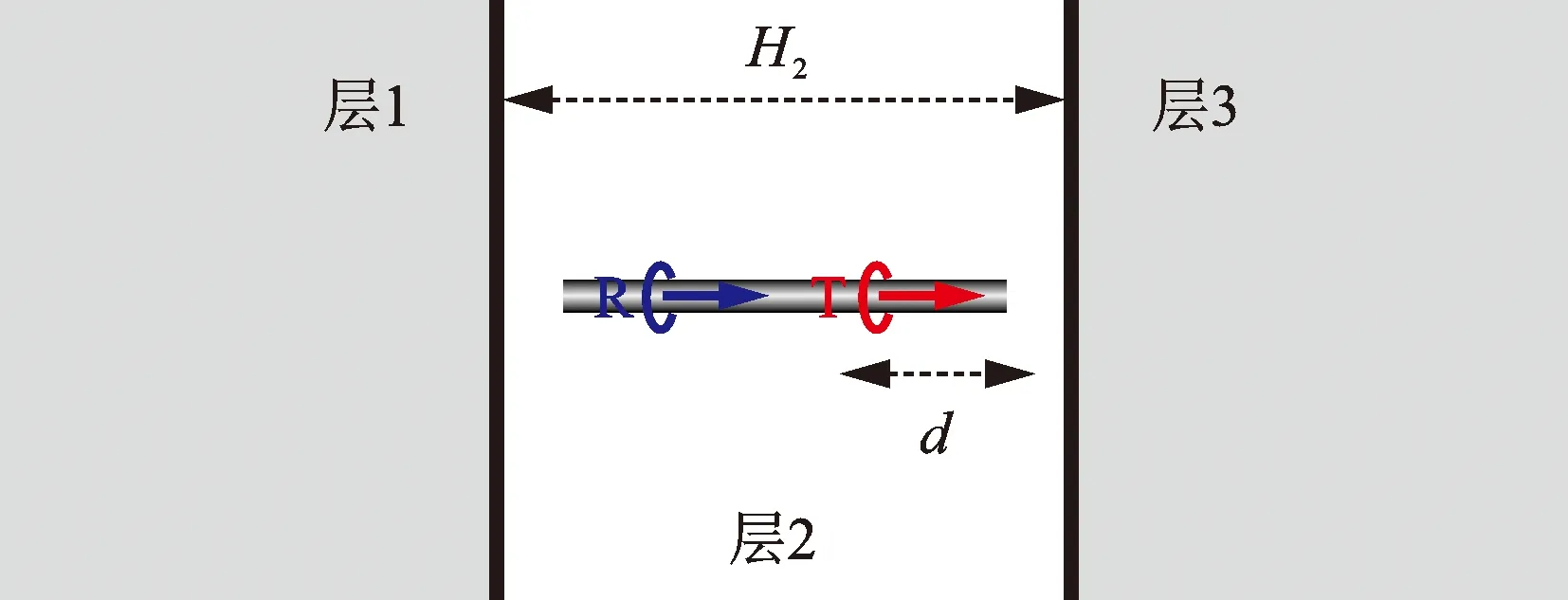
图6 三层模型Fig.6 3-layer formation model

图7 不同层厚的三层模型晚期和全区视电阻率Fig.7 Late-time and all-time apparent resistivity of 3-layer model with different thickness
从晚期和全区视电阻率结果可以看出,曲线与均匀地层曲线发生偏离的时间取决于距离仪器最近的界面,仪器向上或向下移动相同距离时的感应电动势完全相同,图8中两个虚线框位置的响应一致。当中间层为高阻,两侧为低阻围岩时,如图9所示,涡流在一侧遇到距离较近的低阻界面时,另一侧的涡流依然位于中间层,与仪器位于中心点的4 m厚地层相比,低阻围岩的贡献相对要小,但是与10 m厚地层相比,低阻围岩的贡献相对要大,所以感应电动势曲线介于红线和蓝线之间。中间层为低阻的响应较复杂,如图10所示,约10-4s之前距离较近的高阻围岩的贡献使视电阻率曲线介于红线和蓝线之间;但是10-4s之后,高阻围岩以阻碍作用为主,使涡流更集中在当前低阻层流动,导致视电阻率甚至比蓝线更小。

图9 水平井仪器位置变化的高阻三层模型视电阻率Fig.9 Apparent resistivity of resistive 3-layer model with tool position variation
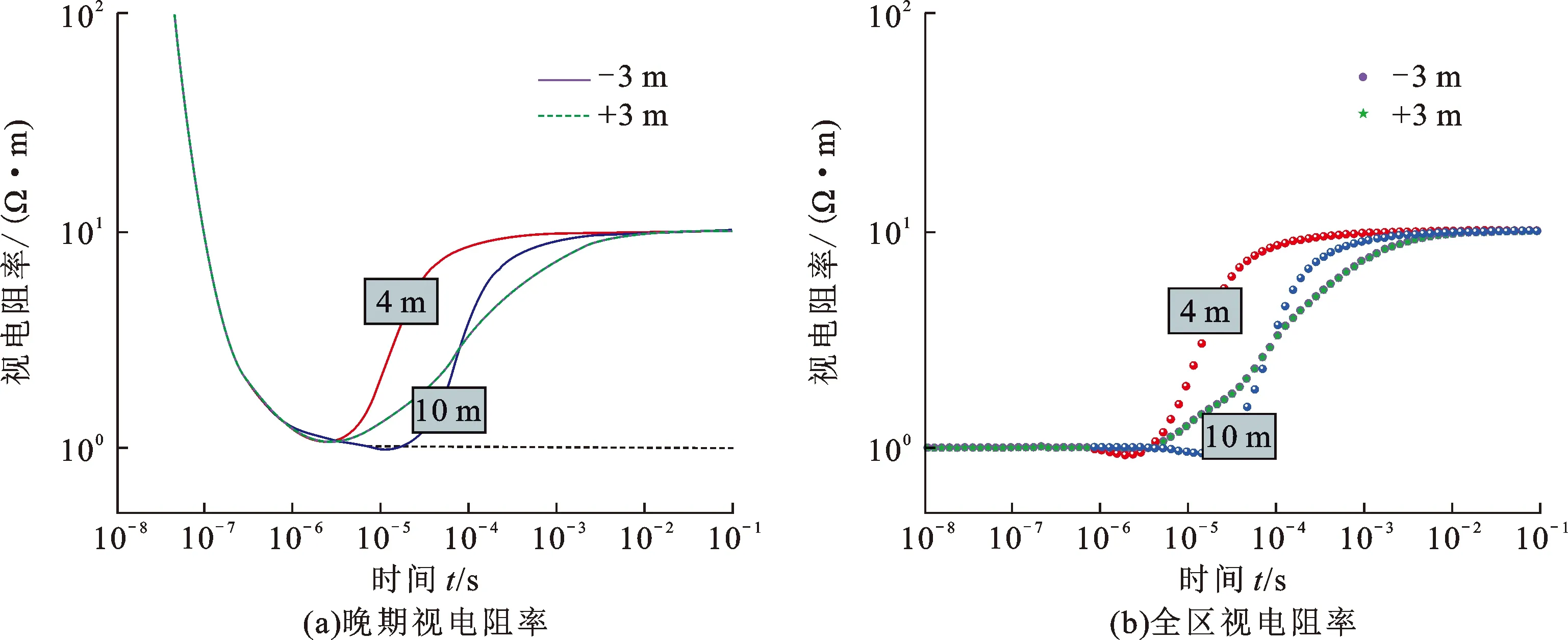
图10 水平井仪器位置变化的低阻三层模型视电阻率Fig.10 Apparent resistivity of conductive 3-layer model with tool position variation
转换后的时域视电阻率曲线反映了地层空间的电性特征,测量早期结果取决于近井地层性质,衰减后期结果反映远井地层信息。大斜度井/水平井的时域视电阻率曲线与方位信息结合使用可为环视地质导向决策提供依据。另外,时谐源随钻电磁波测量信号主要来自周向贡献,对钻前地层敏感性偏弱,导致时谐电磁场前视探测十分困难,而且高度依赖已钻遇地层信息[28]。与之相比,直井条件下的时域视电阻率曲线充分反映了前方界面性质,为钻前地质导向尤其是钻井风险规避方面提供了新的解决思路。
3 烟圈原理分析
瞬变电磁半空间领域的响应特征人们已经非常熟悉,石油测井面临的是全空间地球物理问题,有必要对典型地层的响应机制展开研究。Nabighian的“烟圈”原理对于解释瞬变电磁勘探的响应现象有重要意义[29]:电流源关断间隙在地层中激发感应电动势进而产生环形感应涡流,涡流从发射线圈处随时间逐渐向地层深部扩散,烟圈中心所在位置对应当前时刻的探测深度和接收线圈感应电动势的主要来源。
发射源为z方向的瞬变磁偶极子源,位于模型中心。烟圈扩散图中的黑色虚线表示界面位置,红色、橙色和蓝色等值线分别代表电场中心极值的90%、50%和10%。直井时xoz平面的左半平面与右半平面电场对称,模值相等,所以只给出了右半平面的分布图。
图11表示均匀地层的烟圈扩散图,地层电阻率为10 Ω·m,烟圈随时间向地层深处均匀扩散,烟圈中心始终位于模型的中心线上。
对于两层高阻探低阻模型,如图12所示,发射源所在层电阻率为10 Ω·m,下方1 m处有一个1 Ω·m的低阻界面。可以看出,烟圈中心穿越低阻界面后继续向邻层深处扩散,因此时域衰减后期主要反映低阻邻层电阻率,说明瞬变电磁测井对钻前地层界面具有较强的敏感性,这对前视地质导向具有重要意义。对于两层低阻探高阻模型(图13),发射源所在层电阻率为1 Ω·m,下方1 m处有一个10 Ω·m的高阻界面,代表高能的红色烟圈逐渐远离界面,响应主要取决于当前低阻层,这是低阻屏蔽现象发生的根本原因。高阻邻层只能靠外围能量较低的烟圈去探测,所以后期视电阻率会高于当前层,但与邻层真实电阻率差距很大。
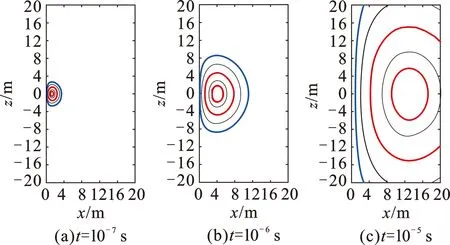
图11 均匀地层烟圈扩散图Fig.11 Smoke rings in a homogenous formation
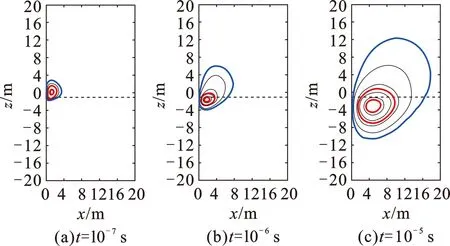
图12 发射源位于高阻层时直井两层模型烟圈扩散图Fig.12 Smoke rings in 2-layer formation when transmitter is located in resistor for vertical well
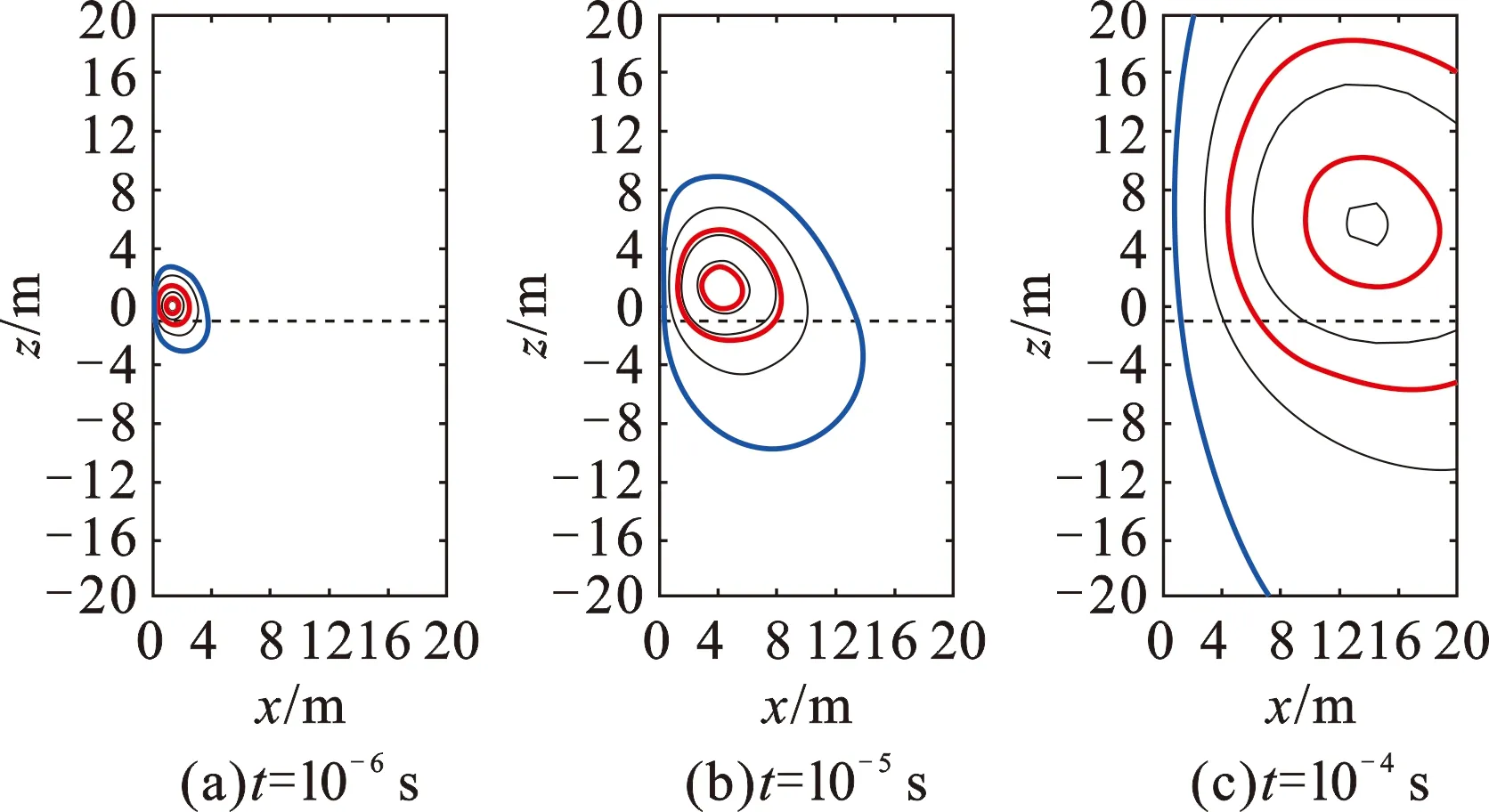
图13 发射源位于低阻层时直井两层模型烟圈扩散图Fig.13 Smoke rings in 2-layer formation when transmitter is located in conductor for vertical well
如果发射源位于电阻率为10 Ω·m的高阻层,围岩电阻率为1 Ω·m,发射源到上下界面距离为1 m,如图14(与图12采样时刻一致)所示,两侧低阻围岩各自都出现了烟圈中心,说明此刻响应来自两侧低阻围岩的贡献。如果发射源位于1 Ω·m的低阻层,上下围岩电阻率为10 Ω·m,如图15(与图13采样时刻一致),烟圈遭到高阻围岩的挤压呈椭圆状分布,高能的红色烟圈逐渐穿过高阻界面,使得高阻围岩的相对贡献缓慢增大,因此图7(a)中视电阻率逐渐逼近高阻围岩真实电阻率,不会出现低阻屏蔽现象。
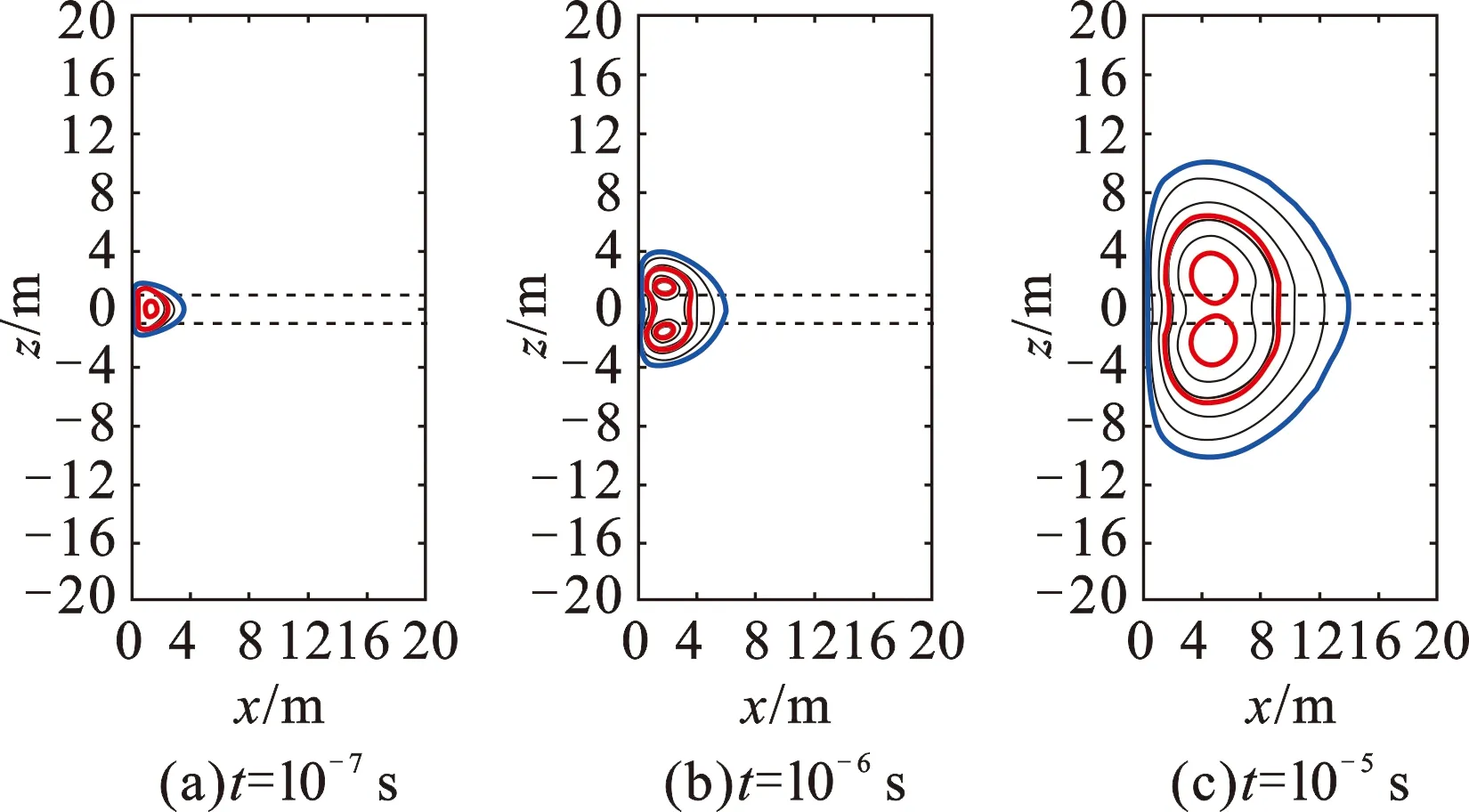
图14 发射源位于高阻层时直井三层模型烟圈扩散图Fig.14 Smoke rings in 3-layer formation when transmitter is located in resistor for vertical well
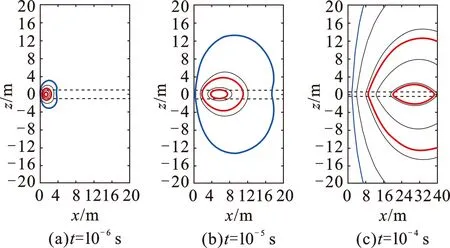
图15 发射源位于低阻层时直井三层模型烟圈扩散图Fig.15 Smoke rings in 3-layer formation when transmitter is located in conductor for vertical well
此外,鉴于直井和水平井视电阻率曲线之间的差异(图4(b)和图5(b)、图7(a)和(b)),一并给出水平井的烟圈扩散图。对于水平井两层模型(图16,发射源位于低阻层),发射源沿z方向,所在层电阻率为1 Ω·m,右侧有一个10 Ω·m的高阻界面,此时左右半平面不对称,所以给出整个xoz平面的烟圈分布。图16与图13相比(二者采样时刻一致),水平井时烟圈高能区域在高阻邻层的分布相对较多,红线甚至可以少部分穿越高阻界面,但大部分依然位于低阻当前层,所以水平井衰减后期视电阻率值比直井要高。
对于水平井三层模型(图17,发射源位于低阻层),中间层电阻率为1 Ω·m,两侧围岩电阻率为10 Ω·m,图17与图15比较发现(二者采样时刻一致),水平井的烟圈中心可以轻易穿越两侧界面向围岩深部扩散,两种情况都可以反映高阻围岩电阻率,但水平井视电阻率逼近围岩电阻率的速度更快。
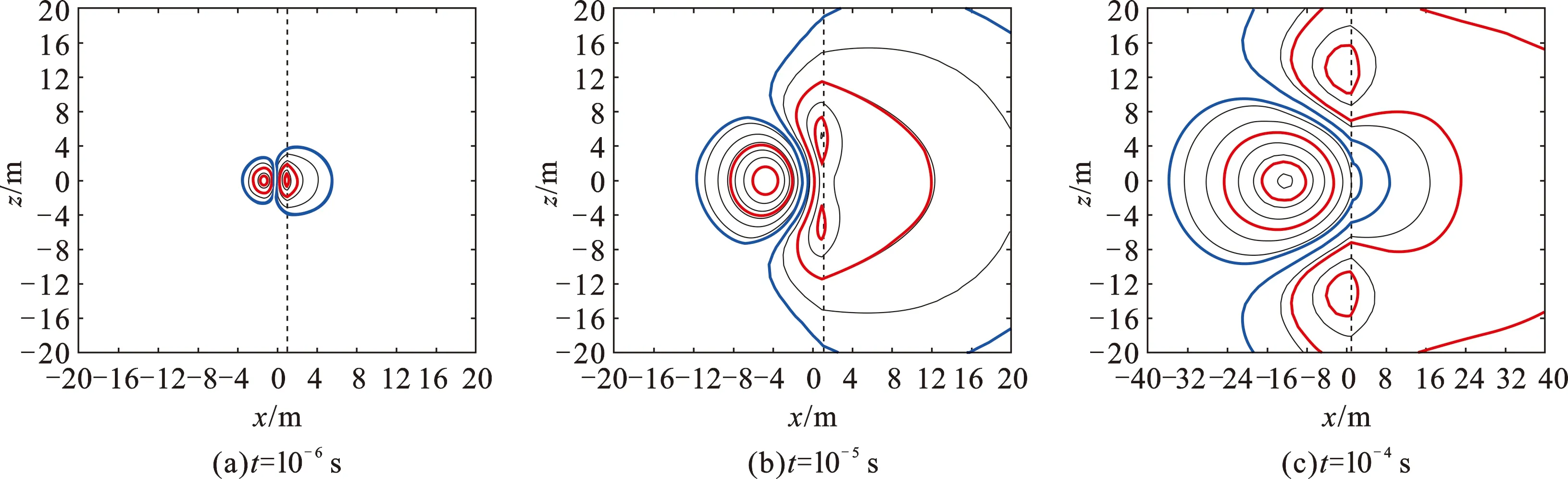
图16 水平井两层模型烟圈扩散图Fig.16 Smoke rings in 2-layer formation of horizontal well
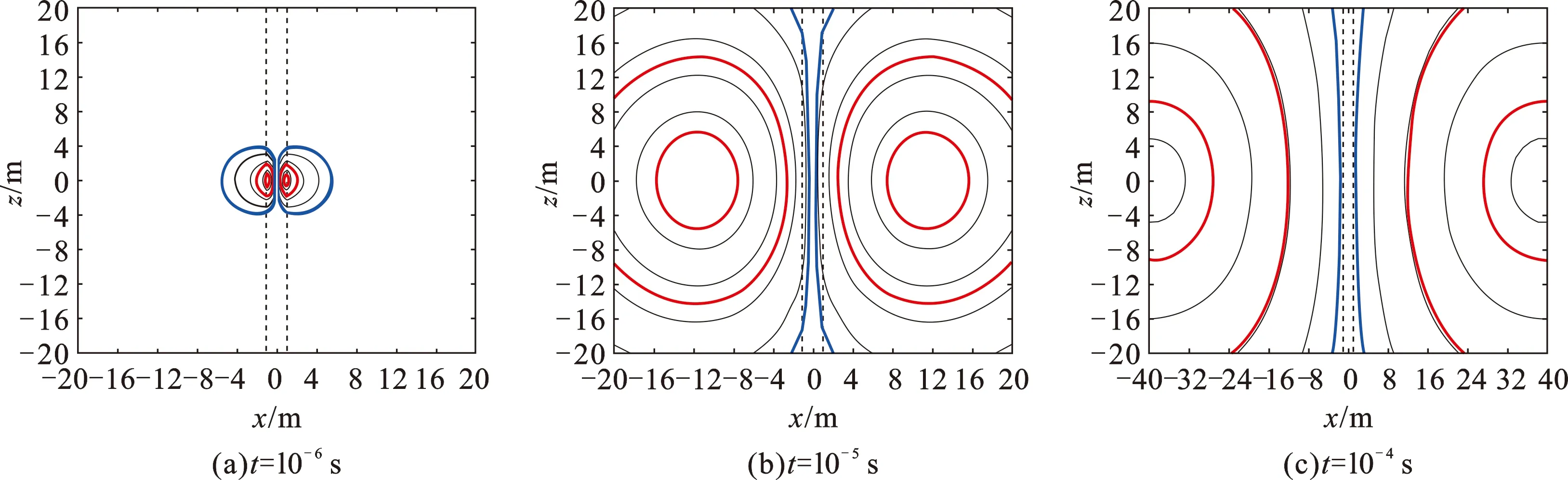
图17 水平井三层模型烟圈扩散图Fig.17 Smoke rings in 3-layer formation of horizontal well
4 结 论
(1)正弦变换的数值滤波与Gaver-Stehfest逆拉普拉斯变换相结合的频-时转换混合算法在保证精度的前提下提高了计算效率,可以为层状介质瞬变电磁测井反演提供快速正演基础。
(2)烟圈在地层中的扩散规律概括为服从“最小能量原理”,即沿着相对容易的路径流动,当发射源一侧有高阻邻层时,烟圈趋向于在当前低阻层扩散,因此出现低阻屏蔽现象;当发射源两侧都有高阻邻层时,反而可以强迫烟圈穿过高阻界面,而不受低阻屏蔽的影响。
(3)全区视电阻率提取方法对于当前层电阻率的判断非常准确,但对邻层电阻率的确定效果依赖地层的电阻率对比,只有不存在低阻屏蔽现象时,该方法才可以在时域衰减后期获得准确的远井地层电阻率。
(4)根据时域视电阻率曲线可以对井周、钻前地层结构变化作出快速预测,为地质导向提供指导,但要实现“时间-深度”对应,判断仪器到界面距离,还需经过进一步反演。
