基于最优桨距计算的风力发电机组控制系统设计

徐枪声，和海涛，郭霖涛，牛焕然

(1.国电投河南新能源有限公司，河南 郑州 450001) (2.许昌许继风电科技有限公司，河南 许昌 461000)

随着风电行业的发展，大型变速变桨风力发电机组如何保持最佳叶尖速比、提高风机在额定风速以下的最佳风能捕获能力、最大限度地增加机组的发电量，是目前风机控制策略的主要研究方向。近年来，国内外学者对变速变桨风力机组的控制策略做了大量的研究，针对提高额定风速以下风机最优控制方案的研究取得了一些有益成果。文献[1]、[2]给出了一种间接的转速控制策略，即在额定风速以下，通过控制发电机的最优转矩输出，实现风机的最大风能捕获；文献[2]～文献[4]提出借助测风设备测得风轮旋转平面的来流风速，依据风机功率特性计算出发电机最优转速的直接转速控制策略，以实现风机在额定风速下的最优运行。以上的研究成果中，无论是间接的还是直接的转速控制策略，因为风轮转动惯量的影响，所以在风速快速变换的情况下，机组都难以快速实现动态的最优追踪。其中基于测量风速的控制方法完全依赖于测风设备的测量精度，需要对整个风轮扫掠面的风速进行处理，在实际工程中的应用效果有限。同时，上述的研究在额定风速以下将叶片桨距角设置为常量，未充分利用叶片在不同叶尖速比下的风能转换效率。

本文在上述研究的基础上提出了一种基于风速估计的风电机组最优功率控制策略，将风力发电机组当作风速仪，以解决风速测量的问题，同时在额定风速以下通过最优桨距控制器计算出最优桨距角，以使风机始终保持最大的功率输出，提高风电机组的发电量。最后基于Bladed Hardware Test模块搭建了硬件在环半实物仿真平台，对所提出的控制策略进行了实验验证。

1 变速变桨风力机组的控制策略

根据空气动力学可将风机吸收功率P表示为：

(1)

式中：ρ为空气密度；R为风轮直径；Cp为风能利用系数；v为风速；λ为叶尖速比，λ=ωrR/v，ωr为风轮转速；β为桨距角。

定义叶尖速比为叶尖线速度和风速的比值，则式(1)可表示为：

(2)

风机转矩T为：

(3)

式中：K为转矩系数。

机组正常运行时，在不同桨距角下存在最大风能利用系数Cpmax和与之对应的最优叶尖速比λopt。由图1可知，当桨距角β=0时，风能利用系数最大为Cpmax，随着叶尖速比的增加，对应的最大风能利用系数先增加后减小。

图1 风能利用系数曲线

风电机组转矩随转速的控制曲线如图2所示，低风速下风电机组运行于最低并网转速N1(ab段)，此后随着风速的增加转矩增加，至最优转矩后进入最优转矩控制；在最优转矩控制bc段运行时风机转矩由式(3)给定，以保证风机追踪最优叶尖速比；当转速达到额定转速Nr时，风机转矩由转矩PID控制器控制，在增加至额定转矩后进入恒功率运行状态[5-6]。

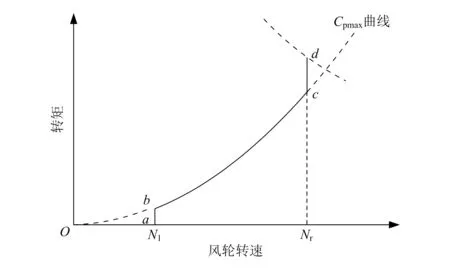
图2 风机转矩-转速曲线

2 最优桨距计算控制器

传统风机控制策略中，为了在最优叶尖速比附近获得更高的风能转化率，通常将Cpmax处较为平缓的桨距角设为固定的最佳桨距角。由图3可知，在额定风速以下机组以最优桨距角β=0°运行时，虽能保证机组在最佳叶尖速比λopt处的最大功率追踪，但在机组叶尖速比高于或低于λopt时，最佳桨距角对应的Cp值偏低。

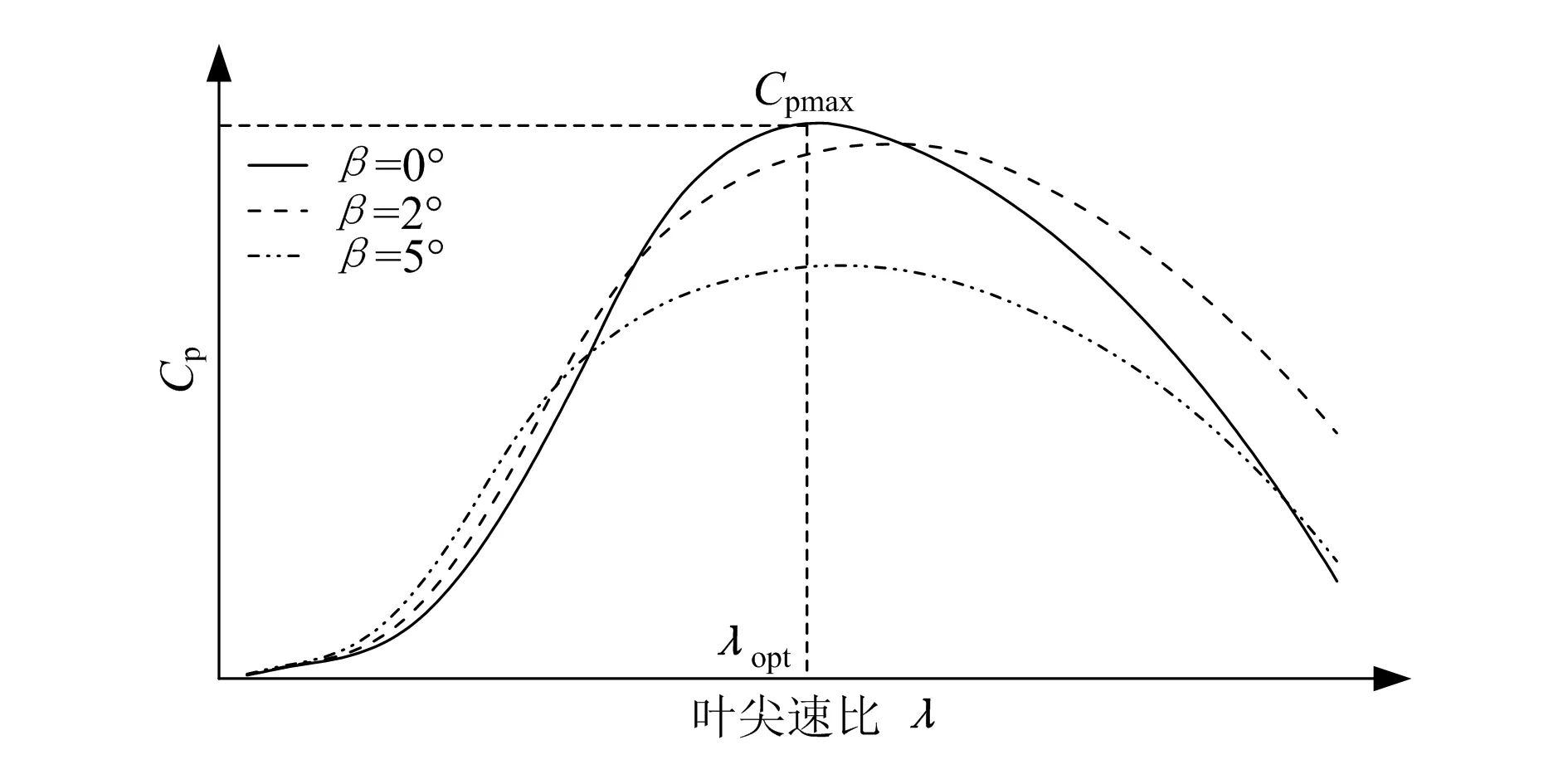
图3 不同桨距角下静态风能转化系数

由此可见，在风速快速变化或由于理论计算结果和实际偏差导致机组实际未在λopt附近运行时，机组的实际风能转化率大大降低。为了进一步提升风力发电机组的风能利用率，本文提出了一种自适应最优桨距角计算控制器，根据机组运行状态实时计算不同叶尖速比下对应的最优桨距角，以实现机组的最大风能捕获能力，提高机组的发电量。

图4所示为某2 MW机组叶片的静态Cp(λ,β)曲线，为了更直观地展现Cp(λ,β)的规律，图中将Cp小于零的部分当作零处理。由图可以看出，在不同叶尖速比和不同桨距角下，叶片的最大风能转化系数有较大差异，整体趋势为随着桨距角的增加叶片最大风能转化系数逐渐减小。基于最优桨距角计算的控制策略为：将叶片的风能转化系数特性数据写入控制器，在机组正常运行过程中实时计算叶尖速比λ，查表计算出与之对应的最优桨距角，实现风力发电机组对风能的最大利用。

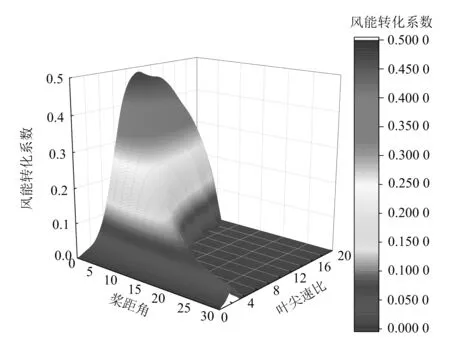
图4 风能转化系数曲线

3 风速估计控制器

为实现风速估计控制策略，基于式(2)的风机功率特性关系，定义函数f(Cp,λ)为[7]：

(4)

风速估计值：

(5)

风机传动系统的运动方程为：

(6)

式中：Tm为风轮机械转矩；Te为发电机转矩；J为转动惯量；ω为风轮转速。

图5所示为桨距角β=0°时函数f(Cp,λ)的特性曲线，函数f(Cp,λ)中的值可通过Cp(λ,β)特性曲线查表计算求出。由图可知，机组在正常运行过程中，函数f(Cp,λ)有唯一的λ值与之对应，即对于测量的发电机功率P、桨距角β和风轮转速ωr有唯一的计算风速值与之对应。

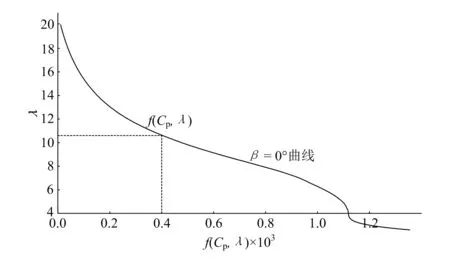
图5 额定风速下f (Cp, λ)曲线

风速估计控制流程如图6所示，驱动风轮的机械转矩与发电机转矩作用于风力发电机组传动系统，随着外界风况的变化，将在传动系统中产生一个变化的风轮转速ω。通过机械和电气损耗修正模型实时计算出风轮实际吸收的功率Propt，之后依据测量的机组风轮转速和桨距角，通过式(4)计算出函数f(Cp,λ)对应的叶尖速比λ，最后通过式(5)对风机风轮面平均的风速值进行估算。

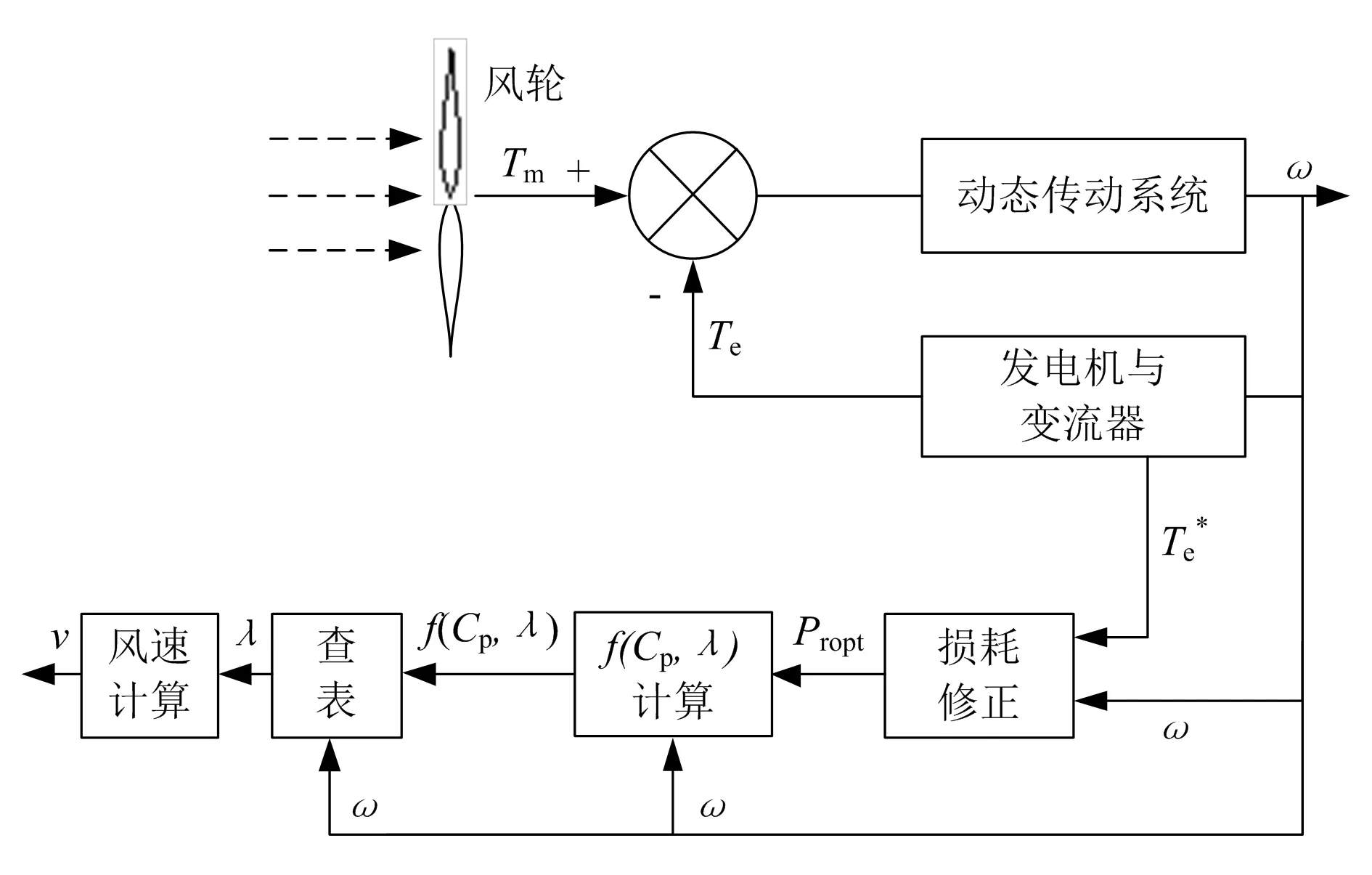
图6 风速估计控制器

基于风速估计的直接转速控制策略中，定义转速参考值ωref为：

(7)

式中：vest为估计风速。

如图7所示，通过风速估计控制器计算出风轮转速参考值ωref，将转速参考值和发电机转速测量值输入到功率PID控制器，通过转速-功率闭环控制方式，使风力发电机转速追踪设定的最佳转速值，进而实现风机的直接转速控制。

基于本节给出的风速估计控制策略，将风电机组本身作为风速仪，解决了直接转速控制过程中风

速测量完全依赖于辅助测风设备精度的问题。除此之外，基于动态的风速估计控制策略，解决了最优桨距控制器计算过程中的风速信号的测量问题，使机组在不同叶尖速比下追踪最佳的Cp值，获得最大的风能转换效率。

4 控制系统建模及半实物平台实验

本文以某2 MW双馈型风力发电机组为例，基于Bladed Hardware Test硬件在环仿真平台，对最优桨距计算和风速估计控制策略进行实验分析。机组为三叶片上风向风机，风轮直径为93 m，轮毂高度为80 m。根据IEC 61400-1风电机组设计规范，在EOG(extreme operating gust)和NTM(normal turbulence model)仿真工况下对风速估计控制器的估计值、最优曲线追踪和发电量等方面进行实验分析。

搭建如图8所示的半实物仿真平台，基于风电仿真软件Bladed Hardware Test的硬件仿真模块实现主控可编程逻辑控制器(PLC)和Bladed的数据交互。通过B&R公司的B&R Protocol通信协议实现PLC与Bladed Hardware Test的通讯，在Bladed Hardware Test软件中设置IP地址，配置测试脚本、通讯协议和数据通道后生成plan文件，将生成的plan文件导入到Bladed中，最后正确设置Bladed后进行半实物仿真实验[8]。

图8 半实物仿真实验平台

4.1 极端阵风下的控制策略响应特性

为验证本文所提控制策略的暂态响应特性，即风速大波动下风速估计控制器对轮毂风速的追踪能力，在EOG工况下进行仿真实验，结果如图9所示。由图可以看出，估计风速与轮毂风速的变化趋势基本一致。由于风速估计控制器是依据风机功率特性进行风速推算的，因此估计值相较于实际风速信号存在一定的滞后，同时因为估计值为考虑风机损耗后整个风轮扫掠面的等效利用风速，模型设置的风速为轮毂某一点的单点风速，所以在阵风前后稳定时间段估计值与轮毂实际风速最大偏差为1.9%，在允许范围之内。由此可以看出，所设计的风速估计控制器在极端风况下对于风速的追踪效果较为理想。

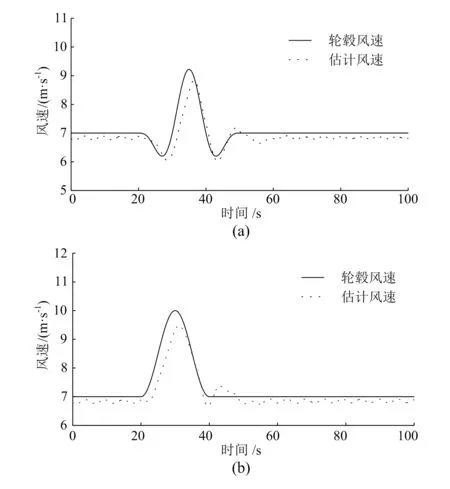
图9 极端阵风下轮毂风速和估计风速

4.2 湍流风况下的控制策略响应特性

为验证本文提出的控制策略在正常湍流风况下的鲁棒性，依据搭建的半实物仿真平台在IEC设计规范定义的正常湍流风况下进行仿真实验，实验测试结果如图10所示。在正常湍流风况下控制器估计风速与轮毂风速的吻合度较高，风速估计值与实际风速变化趋势一致，风速估计信号滤除了风速自然波动的影响，有利于减小桨叶频繁动作对整机载荷的影响，同时更为平滑的风速信号有利于进一步提升风机控制系统的稳定性。

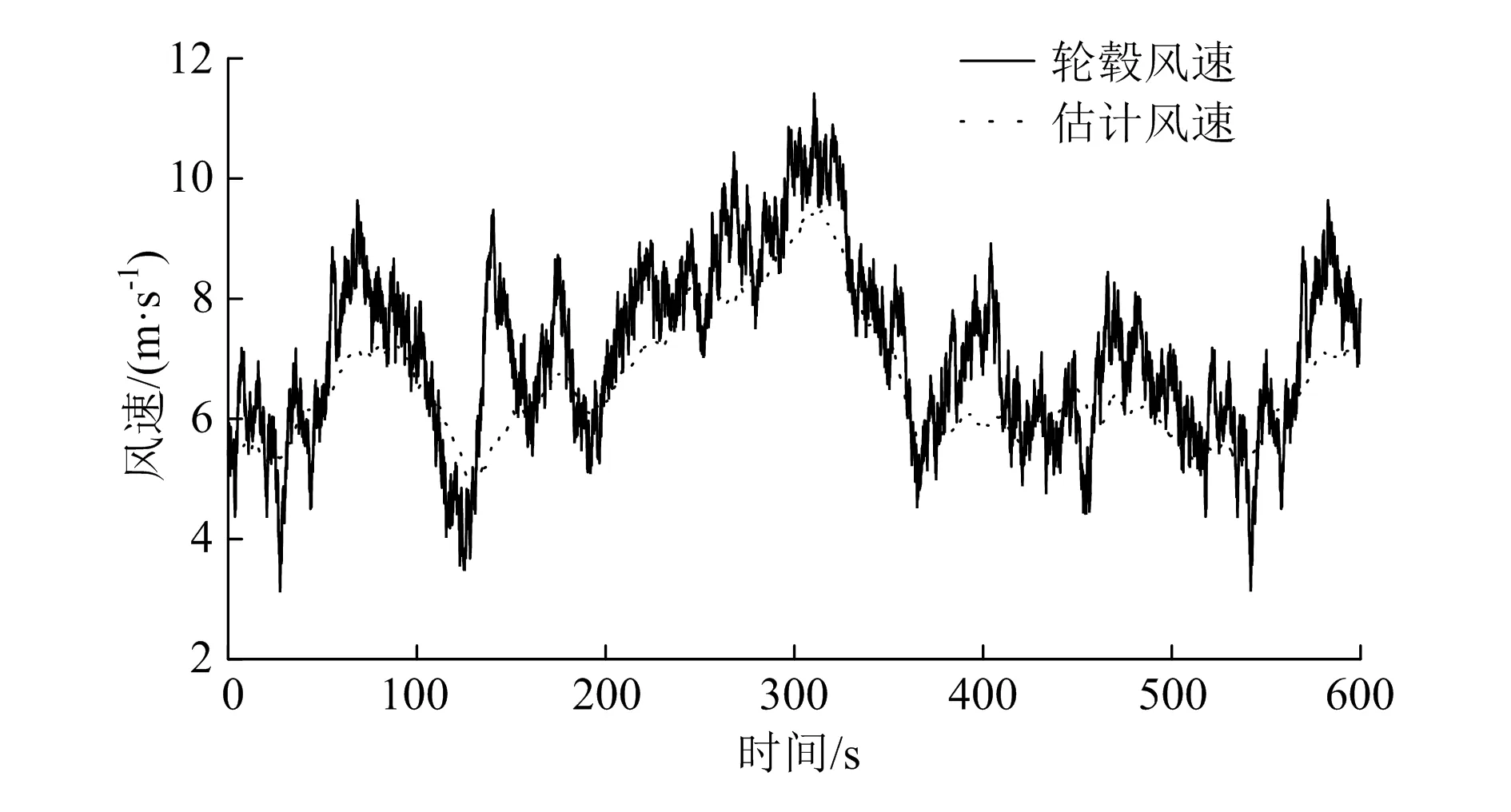
图10 轮毂风速和估计风速值

图11所示为正常湍流风况下机组运行的部分特性曲线，由图11(a)可以看出，基于直接转速控制的闭环策略，风机对设定转速值的追踪性能较好，风机整体运行稳定，控制系统无失稳或震荡情况。由图11(b)湍流风况下机组桨距角变化可以看出，机组在到达额定转速前，最优桨距控制器根据实时叶尖速比计算出对应的最大风能转化系数Cpmax，实现了机组最佳的风能捕获。图中虚线所示的桨距角标志位1表示基于推力消减策略激活变桨动作；桨距角标志位2表示最优桨距控制器激活变桨动作。在正常湍流风况下最优桨距计算控制策略对于风能的转化效率，可用最优叶尖速比进行评判，由图11(c)不同控制策略下机组叶尖速比变化曲线可以看出，正常运行过程中风力发电机组叶尖速比在最优叶尖速比λopt附近波动，相较于采用固定桨距角的传统控制策略，基于最优功率控制策略的机组叶尖速比在λopt附近波动幅度更小，风能利用率更高。

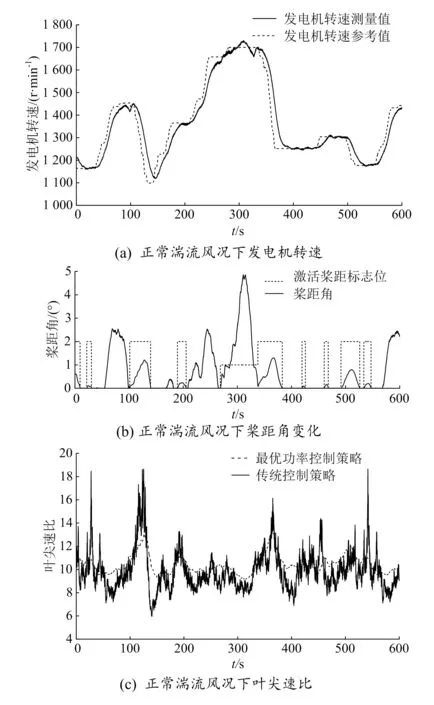
图11 正常湍流风况下机组运行特性

4.3 最优功率控制策略动态发电特性

为验证所设计控制策略的动态发电特性，借助Bladed仿真软件搭建的半实物实验平台，风速间隔设置为0.25 m/s，每个风速对应5个风种子，在标准设计工况下对实验机组在切入风速和切出风速间的动态发电特性进行统计。

仿真实验得到的风机动态桨距角变化曲线如图12所示。由图可以看出，运用本文提出的最优功率控制策略可在最优叶尖速比处维持桨距角在0°附近，当叶尖速比高于或低于最优叶尖速比时适当增加桨距角可以增加Cp值，有效地提高机组的发电效率。

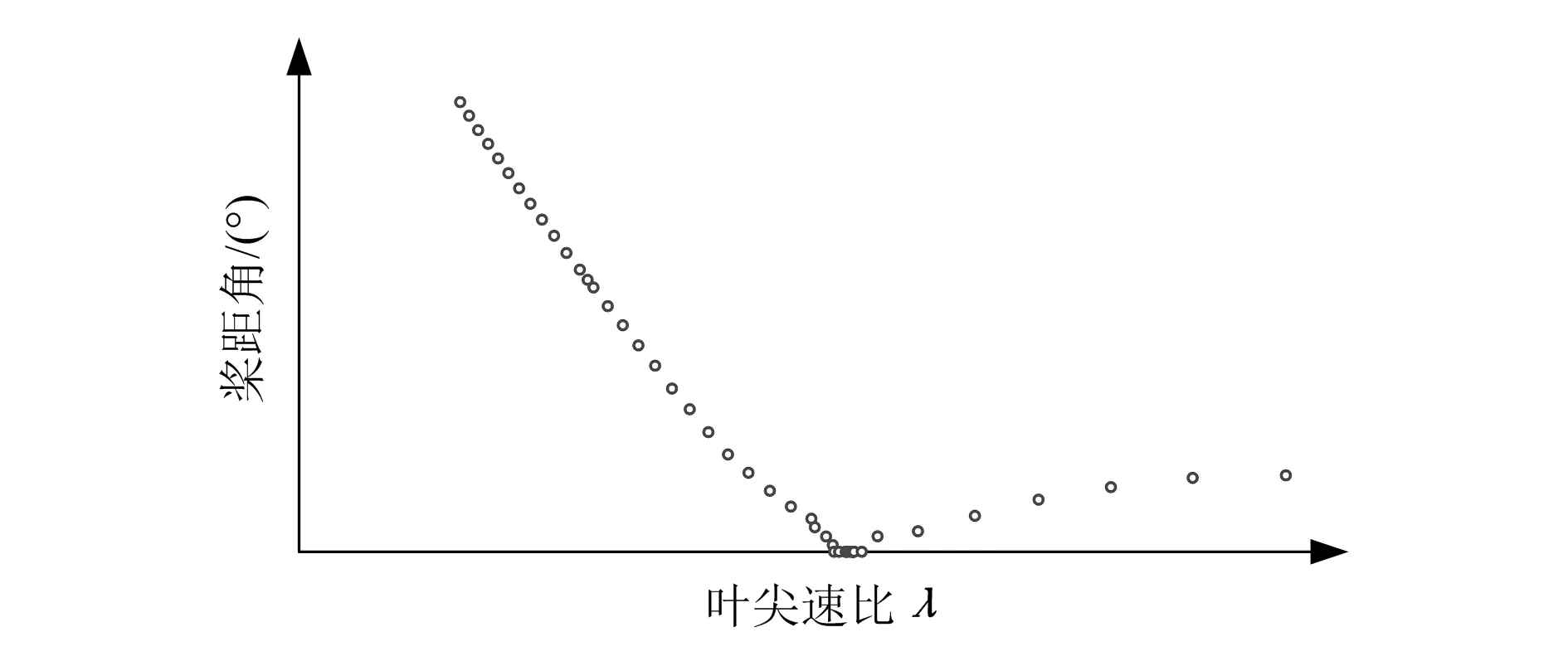
图12 风机动态最优桨距角曲线

以某年平均风速为6 m/s的风电场为例，对仿真实验获得的机组动态功率曲线(风速-功率曲线)数据进行后处理，动态功率曲线和年发电量如图13和表1所示，采用Weibull风速模型计算不同控制策略下单台机组的年平均发电量，见表1。由表可知，采用本文提出的最优功率控制策略单台机组年平均发电量可提高1.3%左右。

图13 不同控制策略下风机功率曲线

表1 不同控制策略下单台机组年平均发电量

5 结束语

本文提出了一种基于最优桨距角计算和风速估计控制器的大型变速变桨风力发电机组最优功率控制策略，可以根据机组运行状态实时计算出不同叶尖速比对应的最优桨距角，在极端和正常湍流风况下对轮毂风速的追踪性能较为理想，保证了风机在不同运行状态下的最大功率输出，有效提高了机组的发电量。