基于混合麻雀搜索算法的作业车间调度研究

李保伟，喻明让，陈 云

(1.中北大学航空宇航学院，山西 太原 030051) (2.北方自动控制技术研究院，山西 太原 030006)

作业车间调度问题(job-shop scheduling problem，JSP)是公认的最困难的组合优化问题，是典型的NP-hard问题。调度问题的难点在于，在多项式时间里，无法找到一个确定的方法来求出该问题的最优解。为了使车间内的生产资源得到充分利用，提高能源利用率，高效的调度方案就显得尤为重要。其中调度优化算法是调度问题的关键点，也是调度问题的研究热点。

群体智能优化算法是调度优化算法的研究热点之一。其主要通过模仿群体的一些行为，在搜索空间内进行全面搜索。因其并行性、稳定性较强，在解决复杂的优化问题时表现出较强的搜索能力[1]。因此，群体智能优化算法被广泛应用到车间调度问题研究中。针对最小化完工时间的目标，李宝帅等[2]改进了鲸鱼优化算法，结合正余弦策略，采用两段式编码使鲸鱼算法可用于解决离散性的JSP问题。徐雨等[3]提出用混合免疫遗传算法求解JSP问题，解决了遗传算法容易陷入局部最优的缺点。阳光灿等[4]提出改进的遗传算法(genetic algorithm，GA)，采用基于操作的编码方式求解JSP问题。赵小惠等[5]采用均匀分布蚂蚁初始位置、多种方式结合进行机器选择的改进蚁群算法求解JSP问题。Ibrahim等[6]提出一种高效的人工藻类与差分进化混合算法来求解JSP问题。针对具有运输时间的JSP问题，鲍蔷等[7]提出一种改进的混合蛙跳算法。近年来，很多群智能算法及其混合算法被用到车间调度问题中，Xue等[8]在2020年提出一种新型群智能算法——麻雀搜索算法(sparrow search algorithm，SSA)，此算法模拟了麻雀觅食、反捕食等行为。目前，SSA及其改进算法已被用到很多研究中。例如，张伟康等[9]对SSA的种群初始化及个体位置更新策略进行改进，在种群初始化方面采用Circle映射策略，在发现者位置更新方面采用蝴蝶优化算法中蝴蝶的飞行方式，从而提高了SSA的全局搜索能力。张晓萌等[10]结合正余弦搜索、多样性变异处理等策略对SSA进行改进，提高了算法的收敛速度和跳出局部最优的能力。刘丽娜等[11]采用量子计算、正余弦搜索等方法对个体位置更新方式进行改进，使算法在后期可以跳出局部最优，在算法迭代过程中加入了高斯扰动、多邻域搜索等策略，让SSA表现出更优越的性能。王建新等[12]采用离散型麻雀搜索算法，对食品安全检查中的抽检路径进行优化求解。此外，SSA还被应用到图像分割、无人机航迹优化和故障诊断等领域。

基于以上研究成果，本文将SSA与GA相结合，并对部分过程进行改进，求解以最小化最大完工时间为目标的作业车间调度问题。

1 作业车间调度问题

1.1 问题描述

作业车间调度问题就是：给定一组作业，其中包含n个工件，要求在m个机器上加工完成，为每道工序分配合适的加工机器以此达到一定的优化目标。做以下假设：1)各个工序在各个机器上的加工时间给定；2)一台机器同一时间仅能加工一道工序；3)一个作业在同一时间只能在一台机器上加工，机器开始加工后不能被中断；4)每台机器在0时刻都可工作且各机器间是独立的；5)每道工序在对应机器上的加工时间是不可变的；6)一道工序的加工时间是连续的，不会出现缺料等情况。

1.2 数学模型

本文所优化的JSP目标是最小化最大完工时间，采用下面的数学模型求解[13]：

f=min{makespan=min max{cik}}

(1)

cik-pik+M(1-aihk)≥cihi=1,2,…,n;h,k=1,2,…,m

(2)

cjk-pik+M(1-xijk)≥pjki,j=1,2,…,n;k=1,2,…,m

(3)

式中：makespan为最大完工时间；cik为工件i在机器k上的完工时间；cih为工件i在机器h上的完工时间；pik为工件i在机器k上加工时间；aihk为指示系数，当机器h先于机器k加工工件i时aihk=1，否则aihk=0；M为充分大正数；xijk为指示变量，若工件i先于工件j在机器k上加工则xijk=1，否则xijk=0；pjk为工件j在机器k上的加工时间；n为工件总数；m为机器总数。式(1)为目标函数，式(2)为工艺约束，式(3)为机器约束。

2 改进混合麻雀搜索/遗传算法

2.1 算法介绍

1)SSA。

SSA模仿麻雀的觅食、反捕食行为进行最优解的搜寻[1]，具有搜索精度高、鲁棒性强、收敛速度快等优点。

麻雀种群通过发现者搜寻食物并向参与者发出信息，参与者追随发现者，侦察者进行反捕食，将危险信息传递给其他个体的行为来进行觅食。基于这一原理，SSA通过发现者与追随者来寻找全局最优解，侦察者则用来防止算法过早收敛，而这些过程在算法中都是通过种群中个体位置更新来实现的。在算法求解过程中，发现者的个体位置更新公式为[1]：

(4)

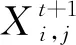
(5)

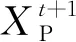
(6)

2)遗传算法。

遗传算法模拟的是大自然中生物的进化规律。遗传算法具有扩展性强、求解流程简单、易与其他算法结合等优点。但遗传算法的搜索速度慢、对初始种群依赖性强，且易陷入局部最优，故多与其他算法结合使用。

2.2 编码及转换机制

1)基于工序编码。

本文采用基于工序的编码，编码由工件号组成，编码的总长度为工序数量，工件号i第j次出现代表第i个工件的第j道工序，即Oij。如图1所示的工序编码所代表的工序序列为O31,O21,O11,O32,O33,O12,O22,O23,O13。

图1 工序编码示例

2)转换机制。

JSP问题是离散性问题，SSA是在连续空间内搜索最优解，因此需要经过编码转换来将SSA应用于JSP问题，具体方法如下：

①麻雀个体位置编码，X=[x1,x2,x3,…,xτ]，其中τ对应工件总工序数，一只麻雀代表一条工艺路线，xi为搜索空间内的实数；

②将编码后的麻雀个体位置按实数xi的值从大到小排列，通过降序函数产生排序后的索引数组A；

③将数组A中的索引除以工件最大工序数，利用正无穷取整函数对结果进行取整，得到各麻雀所代表的工序编码。

2.3 改进的混合麻雀搜索/遗传算法

SSA求解问题的步骤如图2所示。

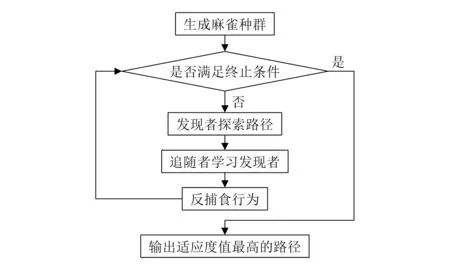
图2 麻雀搜索算法流程

在算法开始阶段，选取种群中适应度较高的麻雀作为发现者，参与者会向发现者学习。由于这一学习行为，使得种群趋于同一个地方，导致算法陷入局部最优，而侦察者的反捕食行为就是为了防止搜索路径陷入局部最优而导致过早收敛。侦察者的数量一般为种群的10%～20%，其数量过大时，会影响算法的收敛速度；数量过少时，会陷入局部最优。

遗传算法主要通过交叉算子来进行寻优，故笔者将交叉操作加入到发现者位置更新之后，用于增强SSA的搜索能力。交叉操作主要有单点交叉、多点交叉与均匀交叉等，本文采用两点交叉的方式来提高SSA的收敛速度。由于GA变异算子的引入可以增强本文所提算法(ISSA/GA)跳出局部最优的能力，故选择逆序变异的方法将其加入到侦察者位置更新后，结合侦察者数量递减策略，提高ISSA/GA跳出局部最优的能力，避免算法过早收敛。

侦察者数量递减策略：在迭代开始时，侦察者设置为较高的比例γ，侦察者数量较多时可以避免种群直接向某个适应度较高的个体收敛，从而错过其他适应度较高的个体，导致种群过早收敛。随着迭代次数增加，逐渐减少侦察者数量，比例降为λ，以保证迭代后期种群的收敛速度。侦察者数量的计算公式为：

(7)

式中：Ps为侦察者的数量；Pt为种群个体总数量；γ,λ为侦察者的数量占比，其中0<λ<γ<1。

混合算法求解JSP的流程如下：

1)设置相关参数，如工件、机器数目等，算法迭代次数、种群数目、交叉概率、变异概率、发现者与参与者数量等，γ和λ的值等。

2)初始化种群，计算个体适应度值，找出当前种群最优和最差个体位置。

3)开始算法迭代，判断是否达到终止条件，若满足条件则输出最优结果，否则重复步骤4)～6)至满足条件为止。

4)根据发现者位置更新公式来更新发现者位置，加入交叉操作，搜索最优解。

5)更新参与者位置。

6)侦察者根据更新公式更新位置，并加入变异操作，更新全局最优个体。

3 实验与结果

为了验证本文所提算法(ISSA/GA)的有效性，通过FT系列算例对不同算法进行测试，比较各算法结果，判断算法的优缺点及性能。本文选取FT06、FT10、FT20为例，采用遗传算法以及ISSA/GA等对算例进行30次求解，并与参考文献[14]中算法的求解结果进行比较。然后对文献[14]中两个实例进行计算，验证ISSA/GA求解JSP问题的可行性。

实验设备的操作系统为64位Windows10，处理器为Intel(R)Core(TM)i5-8300H CPU@2.30 GHz，内存为8.00 GB。编程环境为MATLAB R2020a。

3.1 算例计算结果分析

种群规模为100，最大迭代次数为300，以最小化最大完工时间为目标，对3个算例各独立求解30次，所得结果见表1、表2。表中PSO为粒子群优化算法。

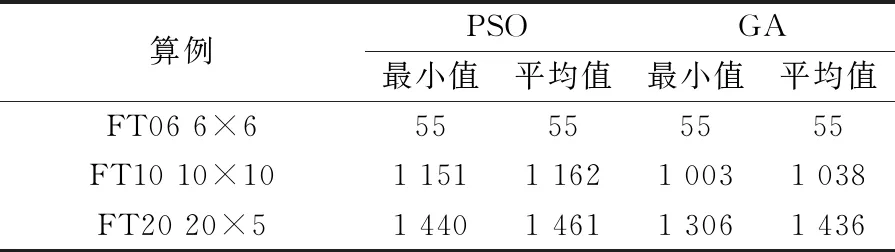
表1 算法测试结果对比Ⅰ 单位：s

表2 算法测试结果对比Ⅱ 单位：s

从表1和表2的求解结果可以看出，在FT06算例中，各算法所得最小值均为55，只有SSA所求平均值为58，可知该算法稳定性稍差。在规模较大的FT10 10×10和FT20 20×5算例中，SSA求得的最小值最差，ISSA/GA所得最小值最优，可知ISSA/GA有较强的搜索能力和稳定性，即在计算小规模问题时，4种算法均有较强的寻优能力和稳定性；在问题规模增大后，在保持较强稳定性的同时，ISSA/GA的寻优能力稍强于PSO、GA及SSA。

由图3可得，在对FT06问题寻优时，ISSA/GA收敛速度最快，最优值与PSO、GA相同。由图4可得，在FT10算例中，ISSA/GA迭代初期就有较快的收敛速度，且最终解最优。综上可得，ISSA/GA的收敛速度快、寻优能力强、稳定性强，是一种可有效解决JSP问题的算法。

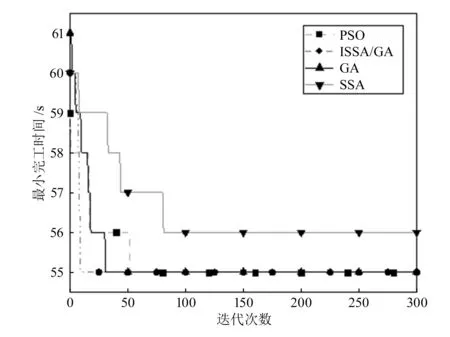
图3 FT06问题寻优结果对比曲线

3.2 实例应用分析

选择参考文献[14]中两个不同规模的实例，使用ISSA/GA对其进行求解，以验证所用算法的有效性。分别选取6×6和10×10的算例，运用ISSA/GA进行求解，算法参数设置与文献一致，最大迭代次数为300，种群规模为50，算法各独立运行30次，得到的结果见表3、表4。

图4 FT10问题寻优结果对比曲线

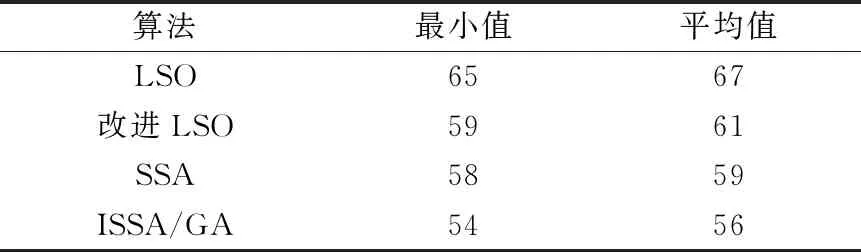
表3 6×6作业车间调度问题寻优结果对比 单位：s

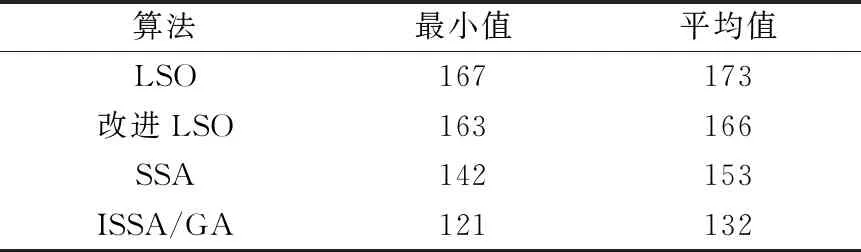
表4 10×10作业车间调度问题寻优结果对比 单位：s

在求解6×6问题时，混合算法取得的最小完工时间是54 s，相较于SSA、LSO、改进LSO所求结果更优。在10×10的实例中，ISSA/GA求得的最小值为121，求解结果明显优于其他3种算法。故而可知本文所用方法在求解JSP时是有效可行的。图5和图6是ISSA/GA所得的最优结果的调度方案甘特图。

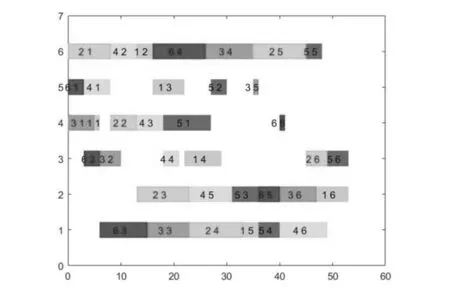
图5 6×6实例调度结果甘特图

4 结束语

高效的调度优化算法是解决JSP问题的关键。

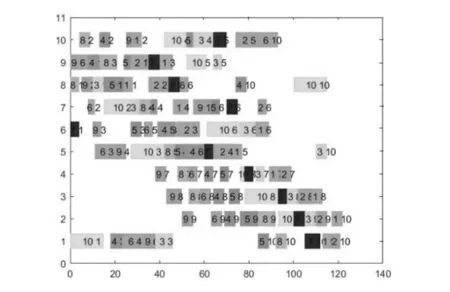
图6 10×10实例调度结果甘特图

本文将麻雀搜索算法与遗传算法相结合，并对其位置编码进行转换，用于解决作业车间调度问题。针对麻雀搜索算法容易出现早熟的问题，采用侦察者数量递减策略并加入变异操作，提高算法性能。通过对FT经典算例的计算结果对比与分析，验证了所提混合麻雀搜索算法在求解作业车间调度问题时的可行性，且具有一定优越性，为JSP的研究提供了一种新的混合算法。

本文所提的混合算法，在单目标JSP问题上可以生成优异的调度方案。而在实际生产中，往往需要考虑多个优化目标，在以后的研究中，可将混合算法用于多目标JSP或IPPS(integrated process planning and scheduling,工艺规划与调度集成)求解。同时，可以采用其他的优化策略来改进SSA，或者将麻雀搜索算法与其他算法相结合来生成更加高效的混合算法。