合理进行多重Logistic回归分析——结合平均处理效应分析

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在进行多重Logistic回归分析时，若自变量中包含“处理变量”，研究者不仅要关注处理变量对因变量的影响是否有统计学意义，还希望了解处理变量取“处理水平”与“对照水平”所产生的因果效应，这两个水平下的因果效应分别被称为潜在结果Y（1）与Y（0）。进一步，还需求出两种潜在结果期望值的差值，该差值被称为平均处理效应（ATE）。本文将介绍如何结合平均处理效应分析，合理进行多重Logistic回归分析的基本思想和具体方法。

1 基本概念

1.1 潜在结果与潜在结果均值

潜在结果（Potential Outcomes，PO）被定义为与受试者相关的独特和内在价值，它描述了一个理想化的数据来源，研究者可以观察受试者对所有可能处理分配的响应［1］。例如，如果数据分析者正在估计一个二值处理变量T的因果效应（设结果变量为Y），其中，T=0表示受试者接受的处理为对照水平，T=1表示受试者接受的处理为真实的处理水平，那么每个受试者都有两个潜在结果Y（0）与Y（1）。受试者水平（也称为单位水平）上的处理效应定义为潜在结果Y（1）-Y（0）的差值。

潜在结果Y（1）与Y（0）各自的期望值被称为潜在结果均值（Potential Outcome Mean，POM）［2-3］，POM的计算见式（1）。

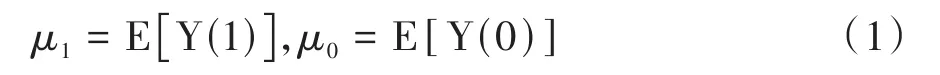
式（1）中，“E［·］”代表求“·”的期望值（即总体均值）。

也可以说，潜在结果Y（1）与Y（0）分别是T=1与T=0条件下，Y的样本均值；而潜在结果均值μ1=E[Y(1)]与μ0=E[Y(0)]分别是T=1与T=0条件下，Y的总体均值。

1.2 平均处理效应

整个总体的平均处理效应有时也称为平均因果效应（ACE）［1］，其计算公式见式（2）。

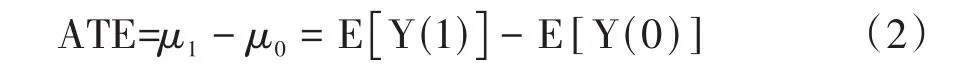
由式（2）可知，平均处理效应在本质上反映了两种处理在总体上的因果效应之差。此差值的绝对值越大，表明处理变量的一个水平相对于另一个水平的作用越大。

1.3 处理组中的平均处理效应

处理组中的平均处理效应（Average Treatment Effect for the Treated，ATET或ATT）是处理组中的个体之间的平均因果效应［1］，其计算公式见式（3）。

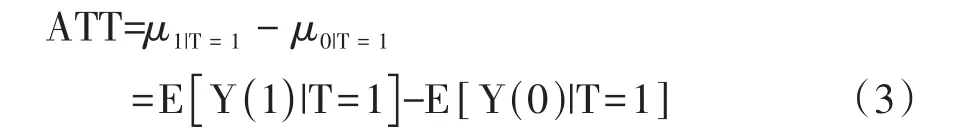
式（3）中 ，μ1|T=1=E[Y(1)|T=1]与 μ0|T=1=E[Y(0)|T=1]是处理组中分别接受真实处理与未接受真实处理的潜在结果。

1.4 逆概率权重

在估计上述提及的统计量（POM、ATE和ATT）时，需要对每个个体赋予不同的权重。有学者提出“逆概率加权”的方法［4］，即以受试者进入处理组的概率的倒数作为权重，代入估计统计量的公式中去计算。也就是说，构建二值处理变量的处理水平关于协变量的多重Logistic回归模型，求出各个体在二值处理变量上的预测值（即概率，也被称为倾向性评分）。当个体属于处理组时，求出的概率P保持不变；当个体属于对照组时，求出的概率P需进行简单变换，即修改为Q=1-P。与这些个体对应的权重分别为1/P与1/Q。

2 估算方法

2.1 估算方法简介

SAS/STAT的proc causaltrt过程中介绍了6种与处理变量的因果效应统计量估计有关的方法［1，4］。通过拟合处理变量T或结果变量Y或两者的模型来调整混杂变量的影响。在model语句中指定结果变量Y，在psmodel语句中指定处理变量T，通过在proc causaltrt语句中使用method=选项指定估算方法（若未使用method=选项，系统将使用默认估算方法）。

6种估算方法包括：①逆概率加权（IPW）估算法；②具有比率调整的逆概率加权（IPWR）估算法；③具有比率和尺度调整的逆概率加权（IPWS）估算法；④增强的逆概率加权（AIPW）估算法；⑤逆概率加权回归调整（IPWREG）估算法；⑥回归调整（REGADJ）估算法。在使用前5种估算法时，使用者必须在psmodel语句内为处理变量指定模型；而在使用第四种和第五种估算法时，使用者还必须在model语句内为结果变量指定模型；在使用第六种估算法时，使用者只需要在model语句内为结果变量指定模型。

2.2 估算方法的要求

使用者可在proc causaltrt语句的method=选项中指定估算方法，并且，还可在model语句和psmodel语句中提供特定的附加建模信息，如表1所示。

表1 估算方法的要求Table 1 Requirements for estimation methods

2.3 具体的估算方法

因估算方法比较复杂，此处仅给出上述提及的6种估算方法中的前3种估算方法的计算公式，其他估算方法的计算公式见文献［1，4］。

Proc causaltrt过程使用psmodel语句中指定的效应将Logistic回归拟合到倾向性评分模型。然后通过取估计的倾向性评分的倒数来计算逆概率权重。假设使用者有观测值（yi，ti，xi），其中，i=1，2，…，n。倾向性评分模型的参数估计值由给出，倾向性评分的预测值计算公式见式（4）。

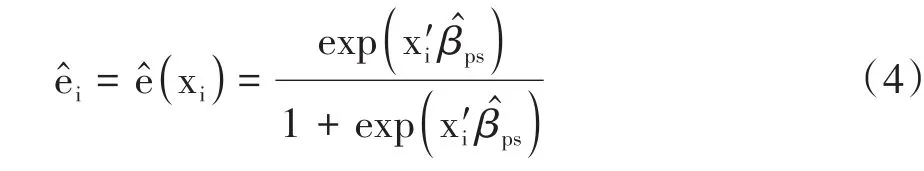
Proc causaltrt过程实施的三种加权方法通过求解式（5）获得潜在结果均值的无偏估计。

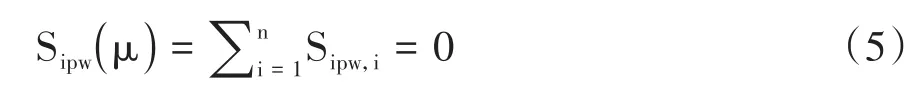
对 于 μ =(μ0，μ1)，其 中 ，Sipw，i的 计 算 公 式见式（6）。

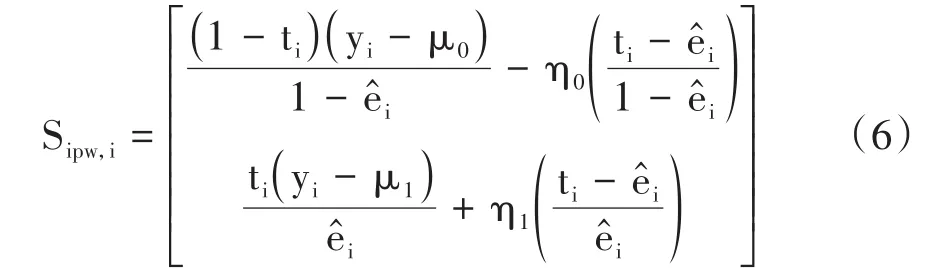
这些估算方法在（η0，η1）的值上有所不同。每种方法的（η0，η1）选择和相应的潜在结果平均值估计的计算公式非常复杂，因篇幅所限，此处从略。

3 实例与SAS实现

3.1 问题与数据结构

【例1】假设在一项临床试验研究中，486名受试者有患2型糖尿病的风险，他们可以选择自己想要接受的两种预防药物中的某一种，研究者不对受试者的任何协变量进行控制。在这项研究中，关注的结果是受试者是否在5年内发展为2型糖尿病［1］。假设数据集Drugs包含以下变量，Age：试验开始时受试者的年龄（岁）；BMI：试验开始时受试者的体重指数；Diabetes2：受试者是否发展为2型糖尿病的指标，其取值为是和否；Drug：处理变量，其取值为Drug_A（对照药）和Drug_X（试验药）；Gender：性别，取值为男性和女性。试分析处理变量Drug对于结果变量Diabetes2的平均处理效应（ATE）。Drugs数据集中的前10个观测结果见表2。

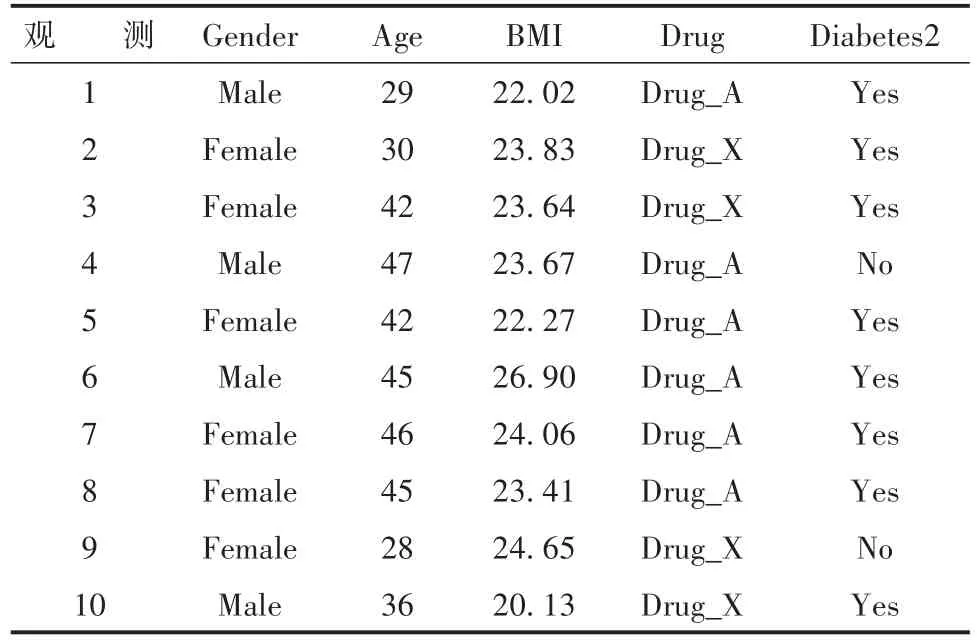
表2 某种药物预防2型糖尿病的临床试验数据结构Table 2 Clinical trial data structure of a drug to prevent type 2 diabetes

3.2 采用传统的多重Logistic回归分析

比较两种药物（Drug_A与Drug_X）中的3个协变量（Age、Gender、BMI）是否具有可比性，发现年龄（Age）在两组之间差异有统计学意义（t=5.420，P＜0.01）。

变量Diabetes2为二值结果变量，可采用二值结果变量的多重Logistic回归分析全部协变量（包括处理变量）对二值结果变量的影响情况。设所需要的SAS程序如下：

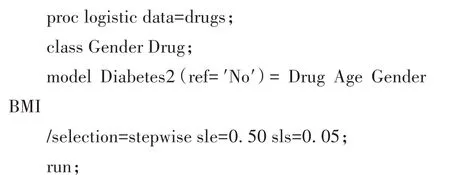
【SAS主要输出结果及解释】上面这段SAS程序的主要输出结果见表3。

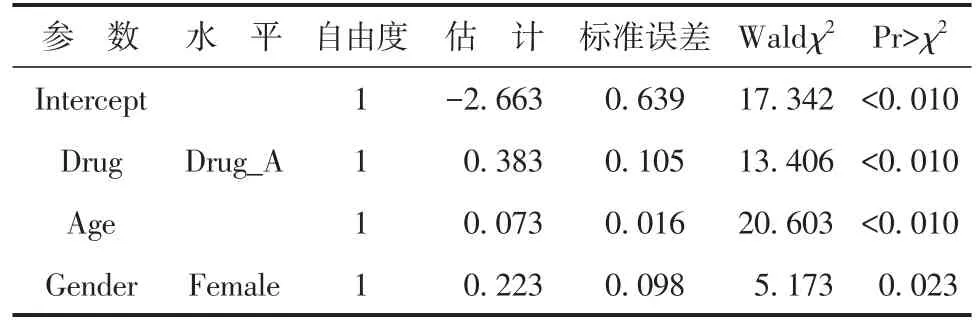
表3 多重Logistic回归模型中参数的最大似然估计结果Table 3 Maximum likelihood estimation results of parameters in the multiple Logistic regression model

以上结果表明：截距项和3个自变量对结果变量的影响均有统计学意义，可以得到多重Logistic回归模型如下：

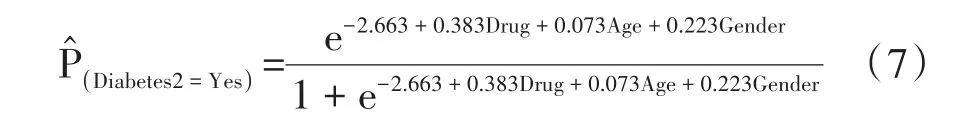
在式（7）显示的多重Logistic回归模型中，研究者最关注的是处理变量Drug对结果变量的影响，其回归系数为0.383，它是“Drug_A”相对于“Drug_X”而计算出来的回归系数。该回归系数大于0，表明与使用Drug_X治疗相比，接受Drug_A治疗的受试者更易于患2型糖尿病。各变量优势比的估计结果见表4。

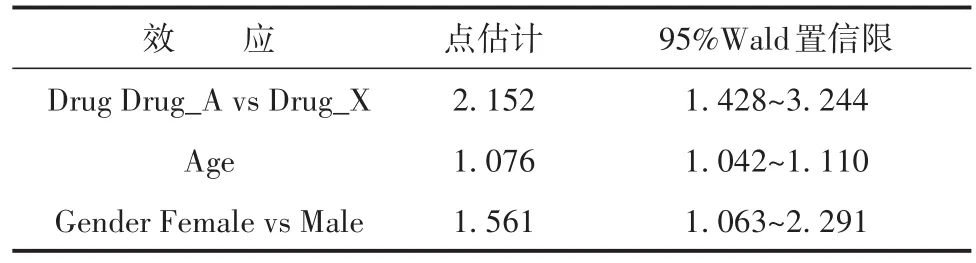
表4 各变量优势比的估计结果Table 4 Estimated results of odds ratio of each variable

由以上结果可知，受试者接受Drug_A治疗比接受Drug_X治疗更易患2型糖尿病的优势比为OR=2.152，95%置信区间为（1.428～3.244）。

显然，传统的Logistic回归分析的结果中，并没有包含变量Drug对于结果变量Diabetes2的平均处理效应（ATE）的估计结果。

3.3 采用causaltrt过程估计平均处理效应

3.3.1 采用逆概率加权法（IPW）进行参数估计

设所需要的SAS程序如下：

【SAS主要输出结果及解释】以上SAS程序的输出结果见表5。

表5是基于倾向性评分分析后，再基于匹配后的数据集并采用IPW法对“结果变量取值为患2型糖尿病”构建Logistic回归模型，得到结果：Drug_X与Drug_A的潜在结果均值（POM）分别为0.459与0.649；两种药物平均因果效应ATE=-0.190，表明Drug_X在预防2型糖尿病方面比Drug_A更有效。正如95%置信区间（-0.290～-0.092）或P值（＜0.01）所示，在0.05水平上，ATE与0之间的差异有统计学意义。

表5 因果效应的分析结果Table 5 Analysis results of causal effects

“ATE=-0.190”的真实含义可用通俗的语言解释如下：因为Y=1代表受试者患2型糖尿病，Y=0代表受试者不患2型糖尿病，故在理论上可认为，某处理组中Y的平均值是一个“隐变量”，它的取值越接近1，表明该处理组中的受试者越易患2型糖尿病；反之亦然。就本例而言，服用Drug_X的受试者对应的Y的总体平均值为0.459，而服用Drug_A的受试者对应的Y的总体平均值为0.649。说明服用Drug_X预防2型糖尿病比Drug_A更有效，使Y的总体平均值下降了0.190。

3.3.2 采用带比率调整的逆概率加权法（IPWR）进行参数估计

设所需要的SAS程序如下：

将“第3.3.1节”SAS程序的第1句中的方法选项修改为“method=IPWR”，其他内容不变。

【SAS主要输出结果及解释】SAS程序的输出结果见表6。

表6是基于倾向性评分分析后，再基于匹配后的数据集并采用IPWR法对“结果变量取值为患2型糖尿病”构建Logistic回归模型，得到结果：Drug_X与Drug_A的潜在结果均值（POM）分别为0.468与0.647；两种药物平均因果效应ATE=-0.179，表明Drug_X在预防2型糖尿病方面比Drug_A更有效。正如95%置信区间（-0.277～-0.080）或P值（＜0.01）所示，在0.05水平上，ATE与0之间的差异有统计学意义。

表6 因果效应的分析结果Table 6 Analysis results of causal effects

3.3.3 采用带比率和尺度调整的逆概率加权法（IPWS）进行参数估计

设所需要的SAS程序如下：

将“第3.3.1节”SAS程序的第1句中的方法选项修改为“method=IPWS”，其他内容不变。

【SAS主要输出结果及解释】SAS程序的输出结果见表7。

表7是基于倾向性评分分析后，再基于匹配后的数据集并采用IPWS法对“结果变量取值为患2型糖尿病”构建Logistic回归模型，得到结果：Drug_X与Drug_A的潜在结果均值（POM）分别为0.469与0.647；两种药物平均因果效应ATE=-0.178，表明药物X在预防2型糖尿病方面比药物A更有效。正如95%置信区间（-0.276～-0.079）或P值（＜0.01）所示，在0.05水平上，ATE与0之间的差异有统计学意义。

表7 因果效应的分析结果Table 7 Analysis results of causal effects

3.3.4 采用增广逆概率加权法（AIPW）进行参数估计

设所需要的SAS程序如下：

将“第3.3.1节”SAS程序的第1句中的方法选项修改为“method=AIPW”，其他内容不变。

【SAS主要输出结果及解释】SAS程序的输出结果见表8。

表8是基于倾向性评分分析后，再基于匹配后的数据集并采用AIPW法对“结果变量取值为患2型糖尿病”构建Logistic回归模型，得到结果：Drug_X与Drug_A的潜在结果均值（POM）分别为0.478与0.649；两种药物平均因果效应ATE=-0.171，表明药物X在预防2型糖尿病方面比药物A更有效。正如95%置信区间（-0.268～-0.074）或P值（0.001）所示，在0.05水平上，ATE与0之间的差异有统计学意义。

表8 因果效应的分析结果Table 8 Analysis results of causal effects

3.3.5 采用回归调整法（REGADJ）进行参数估计

设所需要的SAS程序如下：

将“第3.3.1节”SAS程序的第1句中的方法选项修改为“method=REGADJ”，其他内容不变。

【SAS主要输出结果及解释】SAS程序的输出结果见表9。

表9是基于倾向性评分分析后，再基于匹配后的数据集并采用REGADJ法对“结果变量取值为患2型糖尿病”构建Logistic回归模型，得到结果：Drug_X与Drug_A的潜在结果均值（POM）分别为0.473与0.647；两种药物平均因果效应ATE=-0.174，表明药物X在预防2型糖尿病方面比药物A更有效。正如95%置信区间（-0.273～-0.075）或P值（0.001）所示，在0.05水平上，ATE与0之间的差异有统计学意义。

表9 因果效应的分析结果Table 9 Analysis results of causal effects

3.3.6 采用逆概率加权回归调整的双重稳健估计法（IPWREG）进行参数估计

设所需要的SAS程序如下：

将“第3.3.1节”SAS程序的第1句中的方法选项修改为“method=IPWREG”，其他内容不变。

【SAS主要输出结果及解释】SAS程序的输出结果见表10。

表10是基于倾向性评分分析后，再基于匹配后的数据集并采用IPWREG法对“结果变量取值为患2型糖尿病”构建Logistic回归模型，得到结果：Drug_X与Drug_A的潜在结果均值（POM）分别为0.479与0.649；两种药物平均处理因果效应ATE=-0.170，表明药物X在预防2型糖尿病方面比药物A更有效。正如 95% 置信区间（-0.269～-0.071）或 P值（0.001）所示，在0.05水平上，ATE与0之间的差异有统计学意义。

表10 因果效应的分析结果Table 10 Analysis results of causal effects

【说明】因篇幅所限，以上6小节中“倾向性评分模型估计”的输出结果均从略。

3.4 结论

由“第3.2节”的结果可知，受试者接受Drug_A治疗比接受Drug_X治疗，更易患2型糖尿病的优势比为OR=2.152，它是基于原始数据集得到的结果和结论。值得一提的是，仅采用多重Logistic回归分析，无法获得平均处理因果效应的估计值。

由“第3.3节”的计算结果可知，受试者接受Drug_A治疗比接受Drug_X治疗，更易患2型糖尿病。基于6种估算方法，得到两种药物平均处理因果效应 ATE 分别为-0.190、-0.179、-0.178、-0.171、-0.174和-0.170。相对而言，本例资料采用IPW估算法可以获得绝对值最大的平均处理因果效应值，即ATE=-0.190。它是基于匹配后数据集得到的结果。

4 讨论与小结

4.1 讨论

通常在进行多重回归分析时，假定所有自变量是同时被观测的、互相独立的，完全基于各变量的观测结果并采用统计学处理技术（包括异常点的诊断与处理、共线性诊断与处理）来筛选自变量。事实上，在实际问题中，自变量具有许多不同的特性，例如，从时间角度看，自变量的观测有先后顺序之分，而不是在同一个时间点或时间段上收集数据；从变量的相互关系角度看，有些自变量之间不仅不是相互独立的，还可能存在“中介变量”［1，5］；从研究目的角度看，有些自变量是研究者特别关注的或专门施加的，即“处理变量”［1，6］。另外，在非随机对照研究的资料中，处理变量两水平组的协变量向量之间常不具有可比性，提高协变量在处理变量两水平组之间均衡性的一个有效方法就是采用倾向性评分分析法［7］，通常直接对原始数据集进行回归分析是不合适的。针对具有不同特性的自变量，在进行多重回归分析的过程中，需要采取相应的处置策略或添加相应的分析内容，以便获得更多的、更合理的、更有价值的分析结果。

4.2 小结

本文介绍了与潜在结果均值和平均处理效应有关的基本概念、估算方法、实例及SAS实现。基本概念涉及“潜在结果与潜在结果均值”“平均处理效应”“处理组中的平均处理效应”和“逆概率权重”；估算方法有6种，它们分别是IPW估算法、IPWR估算法、IPWS估算法、AIPW估算法、IPWREG估算法和REGADJ估算法；针对一个假设的药物临床试验资料，用SAS软件实现了多重Logistic回归分析，并采用6种估算方法估计了潜在结果均值和平均处理效应。