一种高速可变形飞行器智能变形决策方法

张 远，黄万伟，聂 莹，路坤锋

(1. 北京航天自动控制研究所，北京 100854； 2. 宇航智能控制技术国家级重点实验室，北京 100854)

0 引 言

以高超声速飞行器(Hypersonic flight vehicle, HFV)为代表的一类高速飞行器结合了航空航天的特点，其具有航程远、速度快、机动强、任务可调整等特点，是实现低成本、可重复天地往返优选技术途径之一，逐渐受到世界各航天大国的广泛关注[1-2]。但是，此类飞行器在总体设计中，同样存在值得进一步优化与完善的问题，如飞行包线大与几何构型单一的矛盾，几何包络大与发射系统受限的矛盾，大攻角飞行/气动热/航程之间的矛盾。如果飞行器能够在飞行过程中根据任务需要，在不同飞行状态下自适应改变自身构型，则可在保证固有约束条件下获得更优的综合性能，进一步扩展飞行器任务边界，为实现全速域、跨空域飞行提供可行性[3-4]。以高速滑翔飞行器为例，在惯性爬升段合理变形减小阻力可减小速度损失；滑翔飞行段合理变形可有效提高升阻比，达到提升航程的目的[5-6]。基于此，高速可变形飞行器的概念应运而生。具体而言，HMFV是指一类能够根据飞行器待执行任务和飞行环境特点实时调整外形结构，以适应更宽空域、更大速域飞行任务的高速飞行器。

按照变形部位及对周围气体产生的不同影响，可分为内流部件变形和外流部件变形两类。前者主要指进气道、发动机喷管等部位发生主动变形，以获得更强动力或者更高的燃烧效率；后者主要指头部、机翼、机身等三类变形，以获得更优的气动特性[7]。20世纪50年代以来，变形飞行器的研究得到了诸多国家高度重视，相继开展了不同层面的深入研究，取得了许多有价值的研究成果，如翼面可弯曲、可变后掠的任务自适应机翼项目，机翼可扭转的主动柔性机翼项目，以及机翼可折叠、可变后掠角的变形飞行器结构等项目[8]。随着材料科学的发展，高速类变形飞行器的研究开始显得具有现实意义。

对于HMFV而言，翼面变形对于气动性能有较大的影响，可带来较大的气动性能上的提升，且易于工程实现与应用，目前也多是采用翼面刚性变形方案[9]。那么“何时变形？何种状态变形？变形量多大？”是我们需要解决的问题之一。一种朴素的思想是飞行任务离线标定，即在飞行前在任务系统中设定好变形方案，飞行器在不同阶段展开不同构型，这种决策方案更为简单且易于工程应用。然而，这种方案无法满足综合性能实时最优的效果，且难以满足任务变更的特殊状况。随着智能材料的发展、滑动蒙皮的应用，可连续变形飞行器的应用已逐渐成为可能。因此，实时智能变形决策问题是HMFV工程应用亟需研究的重点问题之一。针对上述问题，以强化学习为代表的智能思想被应用于飞行器的制导、控制与决策的研究中[10-12]。

强化学习的核心思想是通过感知环境的变化，智能体以“试错”的方式获得奖励的最大值，从而进一步改进动作策略以适应环境[10]。典型的强化学习算法包括Q-Learning、SARSA、动态规划等方法，其是一类动作空间离散的学习方法，擅长处理有限个状态和动作空间的问题。Deepmind团队进一步将强化学习与深度学习相结合，形成了DQN网络，进一步强化了高维问题的解决能力，但是动作空间本质上仍为离散形式。文献[13]以Q-Learning算法为基础，设计带有升力系数、阻力系数和前缘力矩系数在内的奖励函数，以学习获得不同状态下机翼的最优厚度及外倾角；文献[14]用Q-Learning算法实现在爬升、巡航、俯冲三种典型飞行模式下对给定的几类固定外形进行决策，以期获得不同任务下的最优构型，同时设计纵向通道控制律。但决策与控制相互独立，变形决策未考虑对控制效果的影响。文献[15]以一种简化的椭球变形飞行器为对象，基于给定的变形量随变形执行机构驱动电压的变化公式，利用DDPG算法获得适应于整个飞行任务中的决策方案；文献[16]针对后掠角和展长同时可变的无人机进行变形决策，同时将可变形机翼作为控制面，辅助完成滚动和转弯控制；文献[17]基于DDPG对一类仿生飞行器进行后掠角连续变形决策，且利用风洞试验和实际飞行的模拟数据进行对比验证。

综上所述，当前对于变外形飞行器的研究还较少，且研究对象多是低空、低速类无人机，鲜有对HMFV的变形决策问题进行讨论。此外，现有公开文献在变形决策方面的研究所考虑的优化指标较为简单，仅以升力系数、阻力系数或升阻比为单一目标。而对于HMFV而言，在某一套控制增益下，其变形不仅带来气动性能的优化，且带来的较大的参数摄动会对姿态系统的稳定带来不容忽略的影响，因此有必要研究考虑决策与控制的融合问题。本文以HMFV滑翔段飞行过程为例，开展滑翔过程中考虑包含升阻比，稳定性及姿态跟踪能力的综合性能最优下的变形决策研究。首先，基于飞行器动力学模型，对HMFV的关键气动参数进行分析，得出变后掠角对飞行器的定性影响规律；其次，设计考虑综合指标下的智能变形方案和DDPG算法训练框架；再者，设计基础控制器，对带有控制器的可变后掠HMFV变形决策智能体进行训练，获得具备一定泛化能力的决策智能体。最后进行数学仿真，校验方法的有效性。

1 变外形飞行器动力学模型及特性分析

1.1 飞行器模型描述

如图1所示，本文以一种可连续变后掠角的HMFV飞行器为研究对象，后掠角Λ变化范围是30°～90°。由于在飞行过程中，为保持较优气动性能，后掠角会随着不同状态而改变，后掠角的变化将进一步导致关键气动数据的大范围变化，给控制系统带来挑战。因此，本文的研究是基于变外形飞行器受控状态下的变形智能决策问题。为简化建模过程，这里直接给出面向姿态控制的HMFV动力学非线性模型如下：

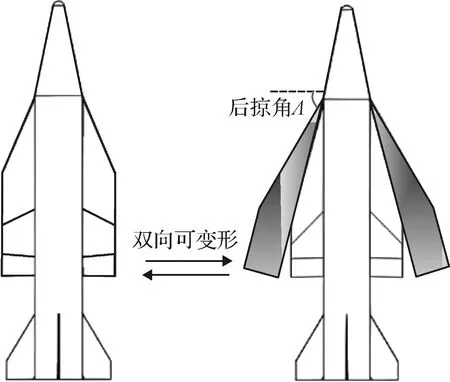
图1 可变后掠高速飞行器示意图Fig.1 Schematic diagram of the variable swept-back HMFV

(1)

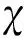
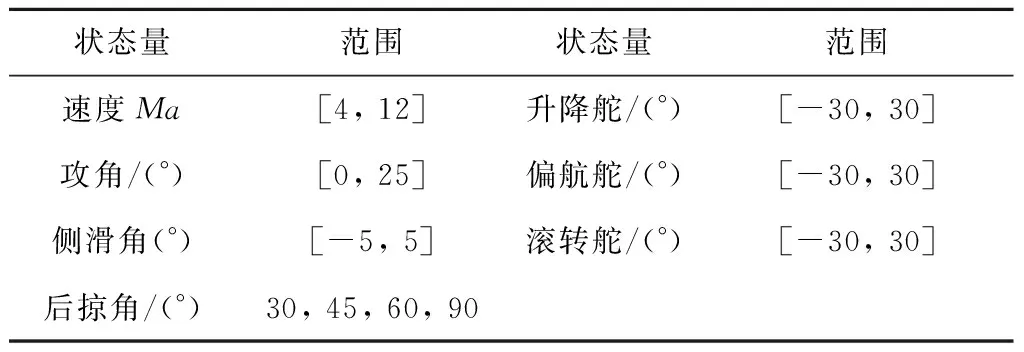
表1 气动插值表状态范围Table 1 The status range for aerodynamics parameters interpolation

(2)

升力Y、阻力D和侧力C可表示如下：

(3)

三通道控制力矩Mx,My,Mz可表示如下：

(4)

式中：Q=ρV2/2为所处环境下的动压；s为飞行器参考面积；ρ为飞行器实际飞行高度下的大气密度；c和b分别是纵向特征长度和侧向特征长度。

1.2 气动特性分析

本文以一类可变后掠HMFV飞行器滑翔段为例，选取了在飞行包线内不同工作点的气动数据，工作点的选取维度包括攻角、马赫数、高度、后掠角。图2～5给出了HMFV在基础构型下(Λ=90°)，不同速度下的部分气动力、气动力矩系数以及升阻比的变化；图6～7给出了HMFV在不同构型下部分关键气动系数在马赫数8下的变化趋势。

由图2可知，零舵偏时，升力系数与攻角近似呈现线性关系，且Ma越大，升力系数越小，攻角越大体现越为明显；类似的，如图3所示，阻力系数在零舵偏下与攻角近似呈现指数关系，阻力系数随着Ma增大而越小；图4为固定构型下的升阻比曲线，总体而言，升阻比在攻角为10°左右达到峰值；图5是俯仰力矩系数随着攻角的变化，在图5所示的攻角范围内，该飞行器表现为纵向静不稳特性。

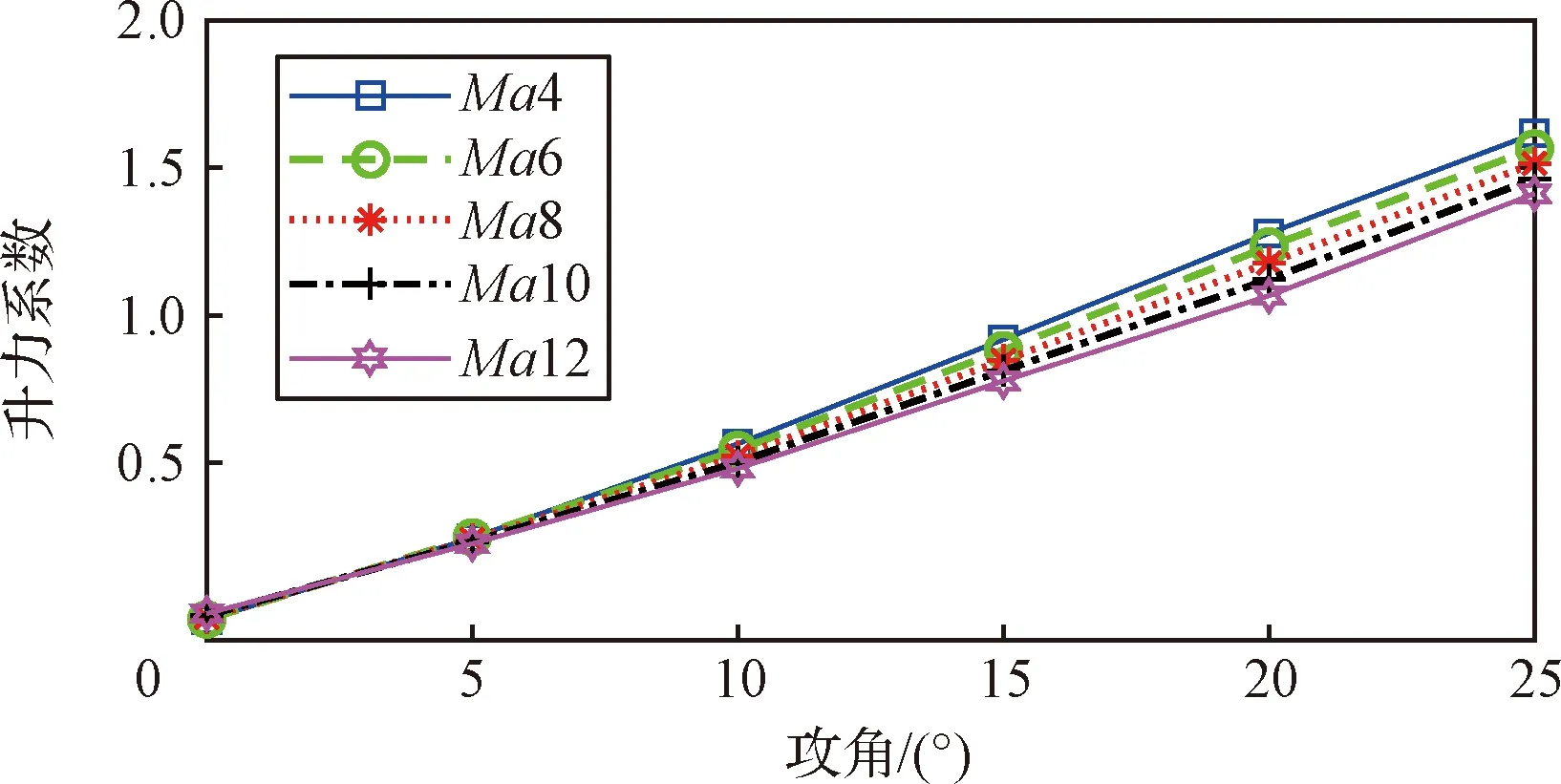
图2 基础构型下不同马赫数下的升力系数变化Fig.2 Variation of lift coefficients at different Mach values for the basic configurations

图3 基础构型下不同马赫数下的阻力系数变化Fig.3 Variation of drag coefficients at different Mach values for the basic configurations

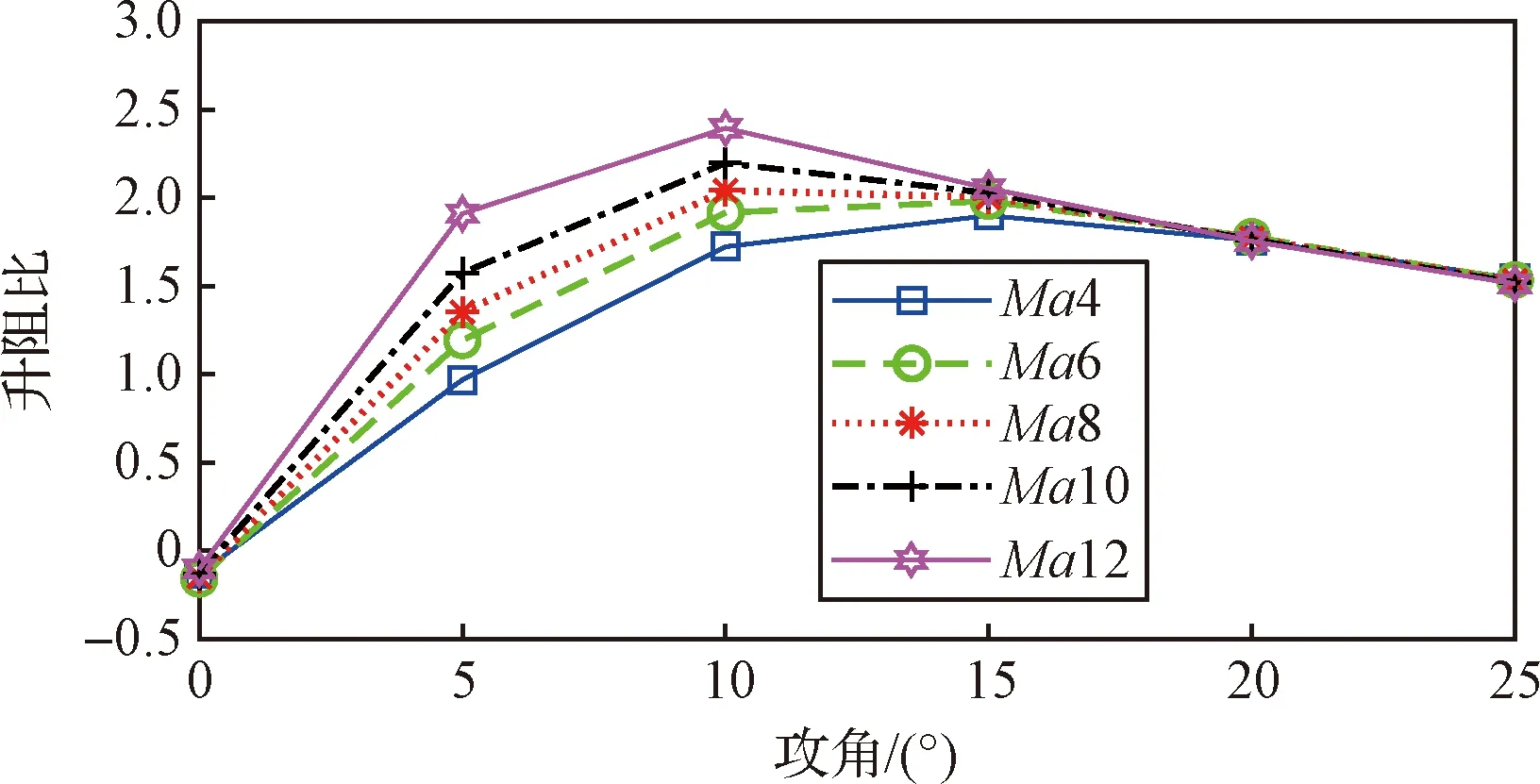
图4 基础构型下不同马赫数下的升阻比变化Fig.4 Variation of lift-to-drag ratio at different Mach values for the basic configurations

图5 基础构型下不同马赫数下的俯仰力矩系数变化Fig.5 Variation of pitching moment coefficient at different Mach values for the basic configuration

不同构型下的气动特性如图6～9所示，图中Λ表示后掠角。由图6可知，随着后掠角增大，飞行器的升力系数随着攻角的增大而减小。分析其原因是后掠角增大，翼的外露面积及翼展长度均减小，进一步带来的升力面减小。同理，由图7可知，随着后掠角增大，因其零升阻力系数和诱导阻力系数均减小，导致阻力系数进一步减小。

图6 四种不同构型下的升力系数变化(Ma 8)Fig.6 Variation of lift coefficient for four different configurations (Ma 8)

图7 四种不同构型下的阻力系数变化(Ma 8)Fig.7 Variation of drag coefficient for four different configurations (Ma 8)

图8 四种不同构型下的升阻比变化(Ma 8)Fig.8 Variation of lift-to-drag ratio for four different configurations (Ma 8)

图9 四种不同构型下的俯仰力矩系数变化(Ma 8)Fig.9 Variation of pitching moment coefficient for four different configurations (Ma 8)

这里仅给出对飞行器影响较大的气动数据变化趋势，对称变形对于横侧向的影响较小，由于篇幅有限，这里不再赘述。由图6～9可以得出以下几点结论：

(1)相比于传统固定构型飞行器，变形飞行器的气动系数不仅与马赫数、攻角等相关，变外形对于气动的影响亦不可忽略。

(2)变形飞行器升阻比随后掠角的增大变化规律较为复杂，在一定攻角范围内(α∈(5°～10°))，变构型对升阻比的影响较大，超过某一范围影响变小。

(4)对于滑翔段而言，不同的攻角、速度下产生最佳升阻比所需要的构型也不同，理想情况下可根据飞行状态调整后掠角，实现滑翔段下的全程最优构型，可达到增大射程的目的。

2 智能变形决策算法设计

本文所研究的可连续变后掠的HMFV飞行器智能变形决策是连续的过程，而某一指标下的最优外形又取决于飞行环境和任务，因此本文将具备环境感知能力的DDPG算法引入到变外形飞行器的智能决策中。本文的研究目标包含三点：1)滑翔段全程实时获得最优升阻比；2)变形的过程中考虑变形对飞行器稳定性影响，考虑在变形和基础控制器作用下使得姿态跟踪误差尽可能小；3)通过训练获得HMFV的变形决策智能体具备一定的泛化能力。

2.1 智能变形决策算法

本文提出的基于强化学习的智能决策方法关键点在于设计强化学习要素，包括环境模型表示、动作空间表示、回报函数设计及动作选择策略。DDPG是一种基于Actor-Critic算法框架下的确定性策略方法，Actor模块进行动作选择，Critic模块进行价值函数评估[19]。为保证算法稳定性，DDPG算法一共设置了两套网络，即在线网络和目标网络。每套网络中又分别包含两个神经网络，即策略网络和值函数网络。因此，DDPG算法中一共包含在线策略(Online-Actor)网络、在线值函数(Online-Critic)网络、目标策略(Target-Actor)网络和目标值函数(Target-Critic)网络四个神经网络结构[20]。定义Online-Critic网络参数为θQ，Online-Actor网络参数为θμ，Target-Critic网络参数为θQ′，Target-Actor网络参数为θμ′，算法实现框架如图10所示。

图10 DDPG算法实现框架Fig.10 The implementation framework of DDPG algorithm

具体而言，DDPG算法执行过程如下:

1)初始化网络参数θQ和θμ，同时将值赋给目标网络，即θQ→θQ′,θμ→θμ′，初始化经验回放池，初始化观测值；

2)根据初始状态值生成变形策略a′，同时添加随机噪声vN,即a′=ai+vN，且vN～N(0,σ2)；

3)执行变形策略a′(变形量)，获得值函数(即奖励)和下一时刻状态向量Si+1;

4)样本数据(Si,ai,ri,Si+1)存储至经验回放池,作为网络训练集；

(4)为了广纳人才，扩大“带头人”的选择范围，选出能真正改变一村经济面貌的“带头人”作为对农村的人才支援，可以采取与“援藏”一样的政策力度，让来自农村的外出务工人员、大学生、公务员都可回原藉参加选举.大学生胜选者可保留学藉，任职结束后仍可选择继续学习，任职经历视同社会实践；公务员胜选者可保留原职，可连续计算工龄，任职结束后仍可回原单位工作.胜选者作为准公职人员管理，根据任职业绩考核计酬.任职能力与政绩表现突出者可直接招录为县、乡级公务员，以拓展农村经济“带头人”的政治前途，激励这些人为一方村民奉献自己的聪明才智.鼓励退休公职人员回乡参加竞选，发挥余热，勇当发展农村经济的带头人.

5)随机抽取经验池小样本(mini-batch)数据，对Actor和Critic网络进行训练，按如下流程更新网络参数；

② 策略梯度反向传播更新给Online-Actor网络参数θμ；按照如下方式梯度更新

③ 以Soft-update的方式更新Target-Actor网络参数和Target-Critic网络参数，即

6)重复在步骤2～5，到达设定的回合数或平均奖励值则停止训练。

2.2 问题描述及智能体训练

如前所述，DDPG算法实现需要状态、动作、奖励函数、神经网络结构以及训练过程复杂参数的设计。考虑到工程应用，首先需要考虑智能体能获得的环境观测值、可执行动作及特性以及与环境交互下的回报形式。针对HMFV的滑翔段决策问题，可观测的状态空间为期望升阻比、当前升阻比与期望最优升阻比的差、姿态角指令、指令跟踪误差。考虑到单个周期下的状态空间训练收敛速度慢，本文充分利用历史数据，使用包含当前状态在内的五个历史周期的数据，将每个状态空间扩张到五维，可有效提升智能体训练过程的收敛效果，形如式(5)：

(5)

式中：αc是攻角指令;λc为期望升阻比;eλ当前升阻比与期望最优升阻比的差;eα为指令跟踪误差;st是状态空间。

1) 由动力学特性分析可知，变形对于俯仰通道的影响较为明显，横侧向通道影响较小，因此本文的决策过程中，仅考虑变形对攻角的影响。同时由于研究的是滑翔段，因此考虑升阻比最优的决策目标。经分析，该飞行器在任意构型下，给定的速度和攻角范围内最大升阻比都小于3，因此本文定义期望升阻比为3，将决策问题转化为跟踪控制。此外，由于本文的智能决策是基于控制闭环状态下的过程，状态空间中的观测值攻角跟踪误差存在与其他观测值数量级不一致的问题，因此在实际训练过程中需要对观测值做归一化处理。

智能体动作输出为飞行器变形指令，即飞行器的期望后掠角：

at=Λtc

(6)

考虑到变形机构的动力学特性，在训练中使用如下二阶动力学特性代替：

(7)

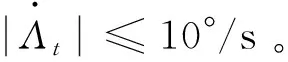
当前回报与智能体当前动作策略输出后得到的姿态偏差、期望的升阻比偏差有关，同时增加单步常值奖励，用于激励智能体尽可能执行完单个训练周期，有助于提升智能体训练的收敛速度。此外，选择最优升阻比跟踪误差eλ和攻角跟踪误差eα为稀疏奖励的判断项，当大于设定值则给一个较大的惩罚。具体奖励函数表达式如式(8)。

(8)

式中：

表2 奖励函数参数设置Table 2 Parameters of reward function

2) 不同于其他文献中的变形决策，本文进一步考虑变形对姿态的影响，为了使得奖励函数设计的更为合理，将变形决策问题统一转化为跟踪问题，同时将观测值归一化，有利于智能体训练的收敛快速性。表2中的参数设置依赖于飞行器特性、决策问题本身以及智能体训练者的经验，可根据问题的侧重点不同调整惩罚因子。

2.3 网络结构及参数设定

本文所用的神经网络结构均为多隐层反向传播前馈神经网络。对于Actor网络，其输入层拥有25个神经元对应25维的环境输入；中间3个全连接形式的隐含层均拥有64个神经元，激活函数为ReLU；输出层拥有1个神经元对应1维智能体的动作，即变形决策量，激活函数为tanh型，添加偏置后可保证智能体的动作量处于设定的范围内，有助于训练的快速收敛。Critic网络同样拥有25维的环境输入，即输入层对应25个神经元，以及1维的动作；状态输入经过2组64神经元的全连接层后与动作输入经过1组64神经元的全连接层的输出进行同维求和，最后再经过一个64神经元的全连接层后输出，输出为1维对应输入状态和动作下的状态行为值，各层激活函数均为ReLU型。本文基于DDPG的智能变形决策算法训练过程中设计网络结构如图11所示。

图11 神经网络结构图Fig.11 Architecture diagram of the neural network

DDPG算法对于超参数较为敏感，一组合适的超参数可有助于训练的快速收敛。根据经验，本文智能体训练使用的超参数设置如表3所示。

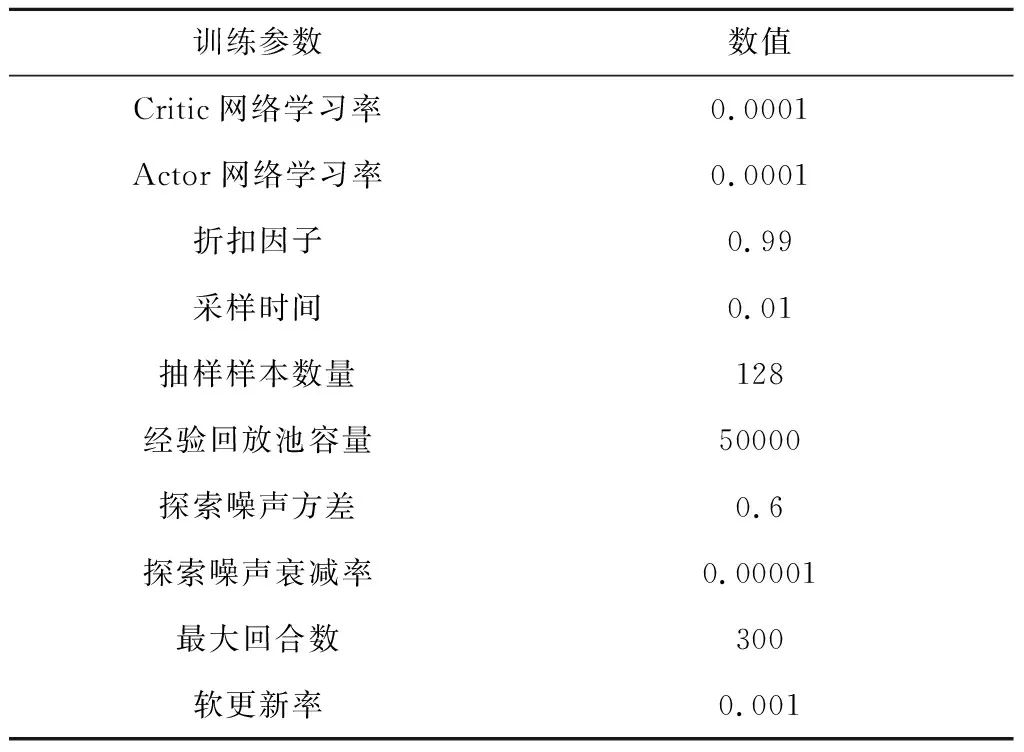
表3 智能体训练超参数设置Table 3 Hyper-parameters for the training agent

回报曲线是反映智能体在训练过程中的收敛性能变化的重要体现。对于带有五拍历史数据的训练过程中，每5个训练回合的平均奖励随回合数变化情况如图12中带有*标记曲线所示。训练开始时，智能体探索初期会存在大偏差状态使得累积回报较小，同时容易触发提前终止条件，得到大的惩罚，因此初期的奖励函数在大范围内变化。在训练40次之后，智能体决策得到的综合指标性能显著提升，收敛效果较好，在90次后满足终止条件。而仅使用当前拍状态作为输入时，智能体训练则难以有效的收敛，甚至无法收敛，其奖励值如图13所示。

图12 带有历史数据的训练累积回报曲线Fig.12 Curves of cumulative reward with history dates

经过动力学特性分析，对于升阻比而言，其主要受马赫数和攻角影响，因此我们可以得到不同速度、攻角下较优的构型(后掠角)。因此可通过插值的方式获得基础决策量作为参考，在此基础上进行“有专家指导”下的训练，相比于其他文献可大大提升训练效率。

图13 无历史数据的训练累积回报曲线Fig.13 Curves of cumulative reward without history dates

3 仿真校验

由于本文研究是变形飞行器的综合性能指标下的智能决策问题，决策因子包含姿态跟踪误差，为了体现决策的有效性，因此本文设计一类基于动态逆的内外环标称控制器。将变外形飞行器动力学模型式(1)整理为面向控制的数学模型式(9)。

(9)

式中：Ω=[α,β,μ]T,ω=[ωx,ωy,ωz]T是内外环的状态；U=[Mx,My,Mz]T是控制力矩；F1,G1,F2,G2分别是标称模型下关于状态的非线性方程：

F1=

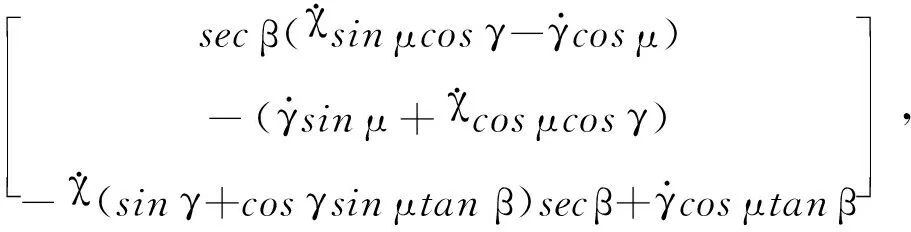
针对式(9)，可基于时标分离假设，分别设计姿态环和角速度环标称控制律，如式(10)所示：

(10)

式中：Ωc是制导系统给出的姿态控制指令，ωc是角速度指令，属于虚拟控制量，且二者微分量可由微分跟踪器获得；K1=diag(5,10,5)是姿态环的控制增益；Κ2=diag(15,50,15)是角速度环的控制增益。

基于标称控制律式(10)及DDPG的框架，本文设计的智能变形决策与控制一体化方案如图14所示。由于本文针对飞行器的滑翔段为研究阶段，核心目标是通过变形提升阻比，进一步提高滑翔距离，同时考虑变形过程对姿态的影响，尽可能减小变形过程对姿态的影响，甚至是通过变形提升单一控制增益下的控制精度。需要说明的是，不同的任务需要设计不同的评价指标，如：爬升段设计升力最优，下压段设计阻力最优。由于实际飞行过程中需要考虑变形机构的特性，因此在训练的过程中以二阶动力学模拟，更具工程应用价值。

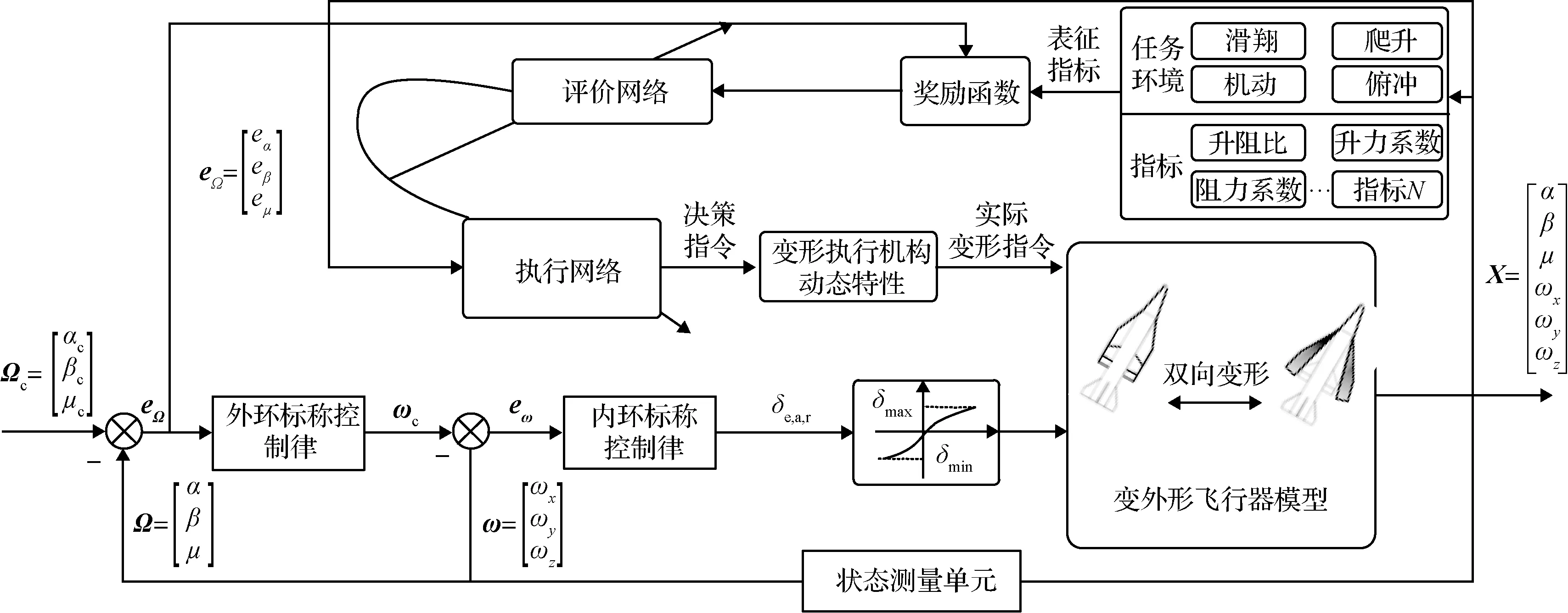
图14 HMFV智能决策控制一体化框架Fig.14 Intelligent decision and control integration framework for HMFV

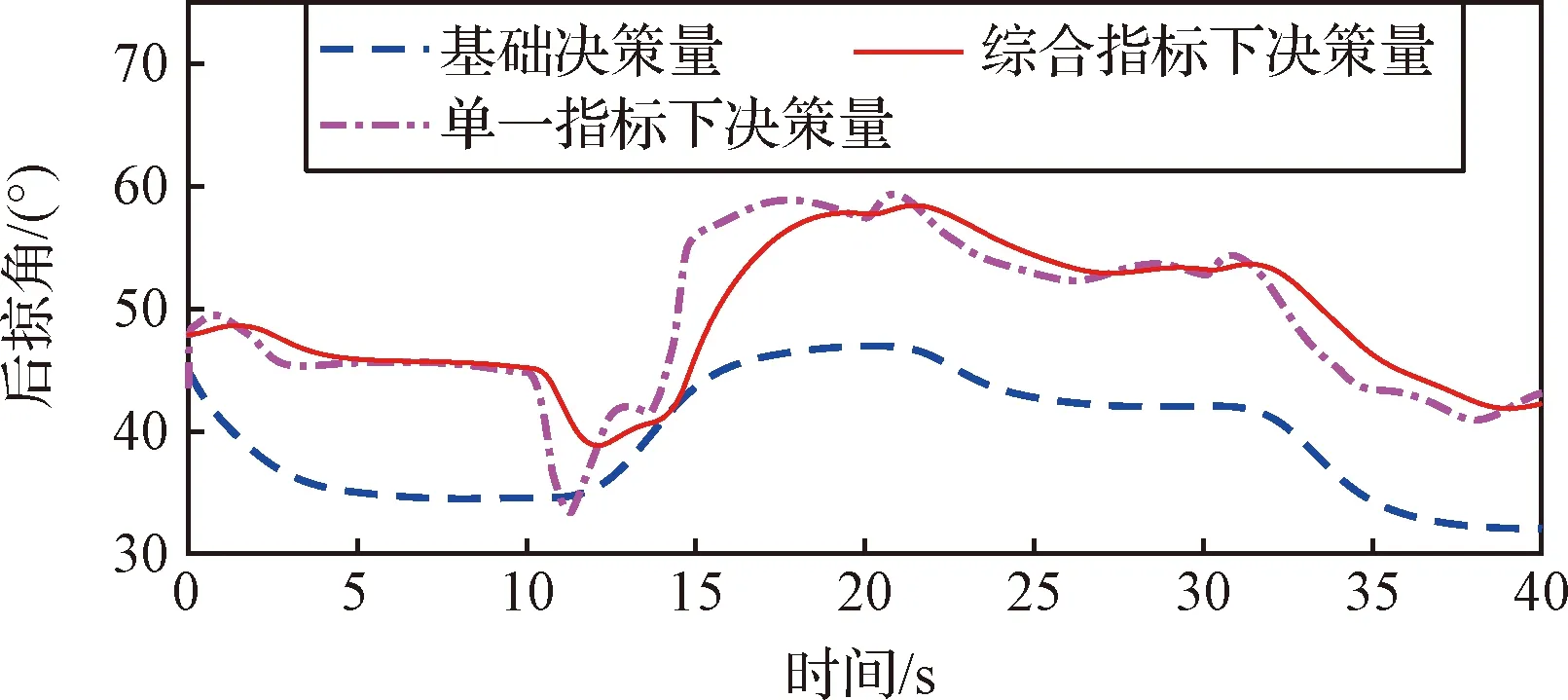
图15 不同决策方式下的变形指令Fig.15 Deformation instructions under different decision methods

在训练过程中，我们仅使用了前20 s的状态，后20 s是训练过程中未遇到的状态，可以看出，所训练的智能体具有较好的泛化性能。图15是通过反插值获得的基础决策量、考虑单一指标和综合指标下训练后得到的智能体在闭环系统中的决策指令输出。从图中可以看出，基础决策量可有效“指导”智能体决策输出。同时，在单一决策指标下仅考虑升阻比，因此变形量变化更加急剧，而综合决策指标下的变形量更为缓和，更加符合工程应用条件。从升阻比的变化看，如图16所示，虚线为基础构型(Λ=90°)下获得的升阻比，点画线为智能体实时决策下的升阻比，实线是反插值方式获得基础决策量下升阻比，可以看出训练后的智能体在不同条件下均可实时获得当前状态下的更优的气动性能。

图16 不同决策方式下的升阻比随状态变化曲线Fig.16 The lift-to-drag ratio variations with status under different decision methods

图17～20是在标称控制律(10)的闭环作用下，使用单一决策指标和考虑指令跟踪误差的综合决策指标两种决策模式下的指令跟踪情况，图17是攻角跟踪响应，图19是侧滑角响应，图20是倾侧角响应。由图18可知，在给定控制增益下，综合指标决策下的变形过程中跟踪误差均有所减小，特别是对于动态跟踪误差表现的更为明显，基于综合决策指标得到的变形决策指令带来的动态跟踪误差减小了近50%，这也表示所训练的智能体在决策过程中实现了综合性能指标最优的目标。

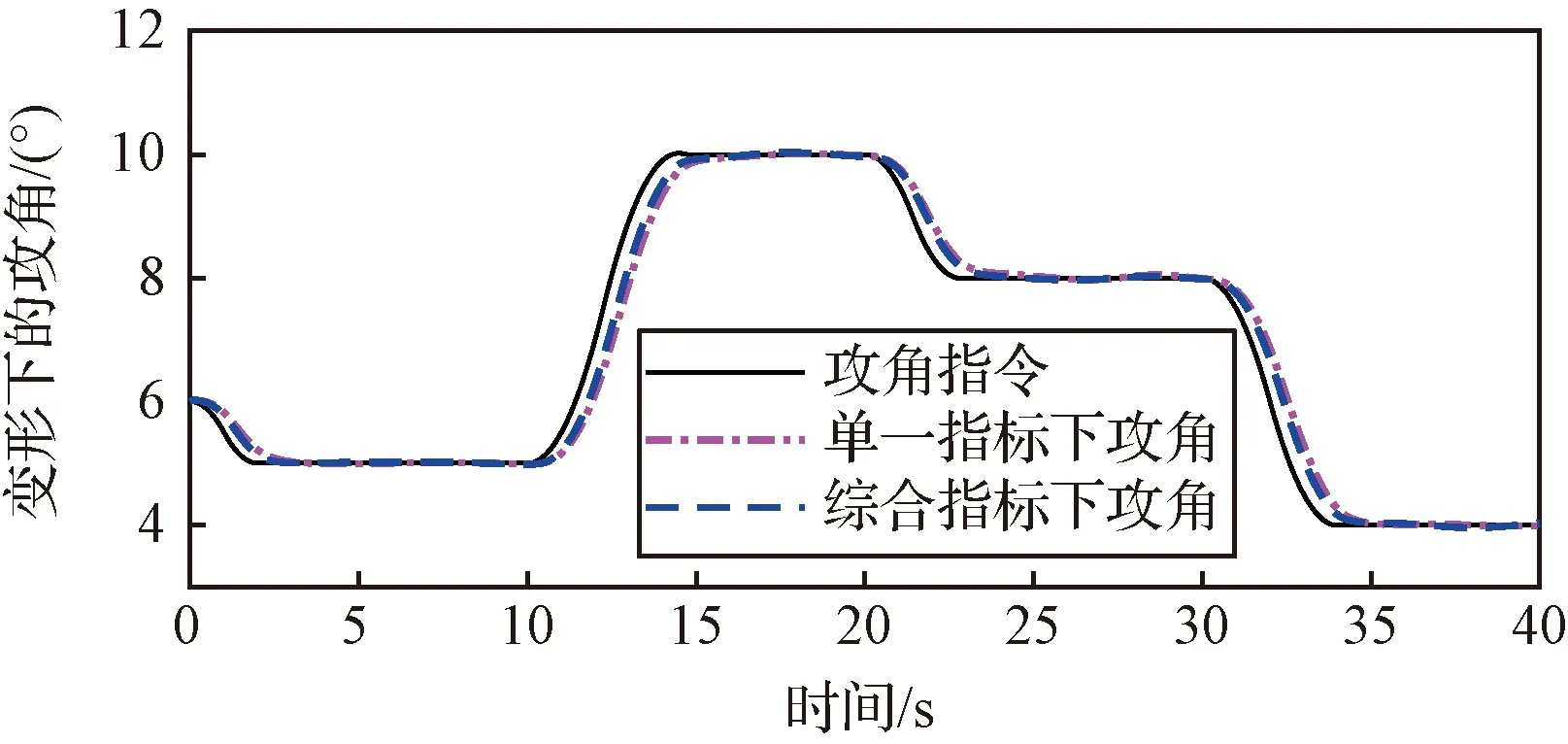
图17 不同决策指标下的攻角响应Fig.17 The attack angel response under different decision indicators

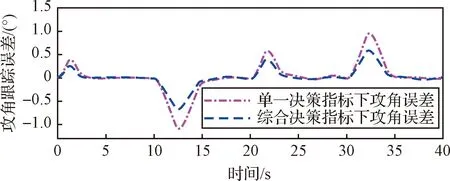
图18 不同决策指标下的攻角误差Fig.18 The tracking error of attack angle under different decision indicators

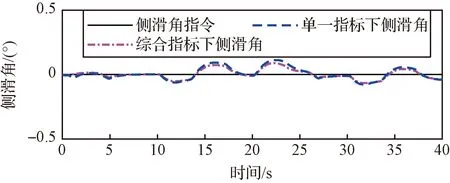
图19 不同决策指标下的侧滑角响应Fig.19 The response of sideslip angle under different decision indicators

图20 不同决策指标下的倾侧角响应Fig.20 The response of bank angel under different decision indicators

需要说明的是，由于升阻比主要受到攻角的影响，且考虑到实际变形时不宜做倾侧转弯，因此本文给的倾侧角指令为0。同时，由动力学特性分析可知，变后掠角的变形形式对偏航通道和滚转通道的影响较小，为了加快智能体训练的收敛速度，仅考虑变形对攻角误差的影响，但是从侧滑角的响应来看，受益于更加合理的变形决策指令，侧滑角的误差也有所改善，达到了预期的效果。

4 结 论

对于一类可连续变形的高速飞行器智能变形决策问题，本文进一步考虑变形决策与控制融合问题，以滑翔段的变形决策为研究目标。首先，基于动力学特征选取合理的决策指标；其次，应用强化学习方法，使HMFV在飞行过程中根据任务、状态条件自主决策实时得到最优构型；再者，综合考虑气动性能指标与稳定性指标设计奖励函数，将决策问题转换为跟踪问题；最后，通过仿真验证本文提出的基强化学习的HMFV智能变形策略可使其有很好的气动性能，同时可以增强变形过程中的飞行稳定。

针对下一步的具体研究工作可以从以下两点进一步开展：1)构造典型任务，实现全弹道、多任务下的实时智能变形决策；2)变形控制与姿态控制一体化研究，一方面获得最佳构型，一方面充分发挥智能控制的作用，生成智能补偿控制律，实现变形过程中的更高精度控制。