大气层内固体火箭多约束鲁棒三维能量管理制导
2022-02-01王松艳
刘 飞,王松艳,杨 明,晁 涛
(哈尔滨工业大学航天学院控制与仿真中心,哈尔滨 150001)
0 引 言
近些年来,固体运载火箭(Solid launch vehicle,SLV)上升段制导受到了国内外学者的广泛关注[1]。基于优化理论,文献[2]利用间接法对固体火箭的上升段轨迹进行了优化,将轨迹优化问题转化为Hamilton两点边值问题,并用数值方法求解。然而,间接法存在两个明显的缺点:由最优条件组成的约束方程非常复杂;数值方法对初值猜想的敏感度较高。相比于间接法,直接法(如高斯伪谱法[3])对于具有快时变和非线性特性的SLV上升段具有更大的工程实践意义。自适应制导算法是近年来的研究热点[4],但在动态参数变化较大的极端情况下,制导算法的可靠性无法得到保证。为了提高轨迹生成效率,许多学者对无损凸优化技术进行了研究,已成功应用到运载火箭[5]、航天器[6]、高超声速滑翔飞行器[7]的轨迹优化中。然而,大多数过程约束和非线性动态都不能无损凸化。近些年来,计算制导引起了学者们的广泛关注。预测校正方法是一种典型的计算制导方法[8],但其对算法的实时性要求很高。
SLV的一个显著特点是发动机推力和关机时间不可控。对此,文献[9]采用了耗尽关机技术,通过改变飞行姿态角来调节所需剩余速度。在过去的几十年里,学者们致力于SLV能量管理算法的研究[10]。Yao等[11]提出了一种单向姿态能量管理方法。文献[12]研究了基于零射程线的耗尽关机能量管理算法,其优点是降低了算法对关机点的灵敏度,但并没有考虑过程约束。Patha等[13]研究了基于交替俯仰角变化的姿态能量管理(Attitude energy management,AEM)方法,但姿态角变化曲线需要离线计算。Wang等[14]提出了一种改进的姿态能量管理,减小由于忽略角速度而产生的跟踪误差。上述方法均未考虑不确定性,在有参数摄动的情况下鲁棒性较差。Zarchan[15]提出的通用能量管理(General energy management,GEM)方法是一种闭环制导算法,其速度控制精度较高,但起始点和结束点的攻角较大,可能会违反过程约束。文献[16]采用样条能量管理方法构建约束方程,利用数值方法在线求解。文献[17]提出了一种基于动态逆的能量管理方法。这两种方法都能实现对终端速度的精确控制,但不能调整终端高度。文献[18]提出了基于推力矢量控制的能量管理的完整方案。上述算法在纵向平面进行能量管理,避免了与侧向运动的耦合,但减弱了速度调节能力。文献[19]引入侧向能量管理消耗剩余能量,从而精确控制终端速度。然而由于纵、侧向机动的耦合,侧向制导指令可能会对终端高度产生影响。文献[20]针对满足多约束条件的标称轨迹,提出了一种离线轨迹优化方法。虽然该算法的精度较高,但不具备在线自适应能力。现有的能量管理算法仅在大气层外进行[21],这导致终端速度调节能力较差。因此,需要开发一种大气内能量管理算法以延长能量管理时间,提高速度调节能力。
结合上述国内外研究现状分析,本文研究的大气层内三维能量管理存在如下难点:
1)由于气动力的存在,难以准确计算剩余速度能力。
2)由于发动机工作环境的差异,导致发动机的比冲和秒流量与地面试验存在差异。理论计算的局限性以及风洞实验与实际飞行条件不同,使得计算时用到的气动系数与真实值存在偏差。这些参数不确定性将影响制导精度。
3)与大气层外能量管理相比,大气层内能量管理需要考虑动压约束。对于在真空中飞行的SLV,过载约束只与当前速度有关。而动压约束不仅与速度有关,还与高度有关。动压约束下的控制量可行域的计算比由过载约束构成的可行域[22]更为复杂。
4)当发动机关机时,SLV需要以零侧向速度回到发射平面。三维制导带来了终端侧向位移和侧向速度约束,这使得终端约束的数量增多,从而增加了制导的复杂性。
基于上述问题,本文提出一种改进的上升段制导算法——基于能量管理的鲁棒三维制导算法(Robust three-dimensional energy management, R3DEM),用以解决考虑模型参数不确定的上升段在线轨迹规划制导问题。引入侧向能量管理对发动机剩余速度能力进行耗散,提高速度调节能力。将闭环制导转化为求解关于攻角和侧向速度能力曲线参数的非线性方程组问题。此外,还考虑了控制量变化率约束、过载约束和动压约束。针对气动系数、发动机比冲和秒流量存在的摄动,利用容积卡尔曼滤波进行模型参数辨识提高了制导算法的鲁棒性。
1 问题描述
1.1 上升段运动模型
在发射坐标下建立SLV上升段运动模型,将三维空间运动分解为纵向平面运动和侧向平面运动,如图1所示。v为SLV的速度;vxy和vxz分别为纵向平面和侧向平面上的速度投影;Pe为发动机推力,其方向沿SLV体轴;Pey和Pez分别为推力在纵向平面和侧向平面上的投影;Θ为当地弹道倾角;Φ为SLV弹体轴线与当地水平面的夹角,称为当地俯仰角;α为攻角;σ为当地弹道偏角;Ψ为体轴与当地纵向平面的夹角,称为当地偏航角;β为侧滑角;D,L和R分别为阻力、升力和侧力;G为重力。
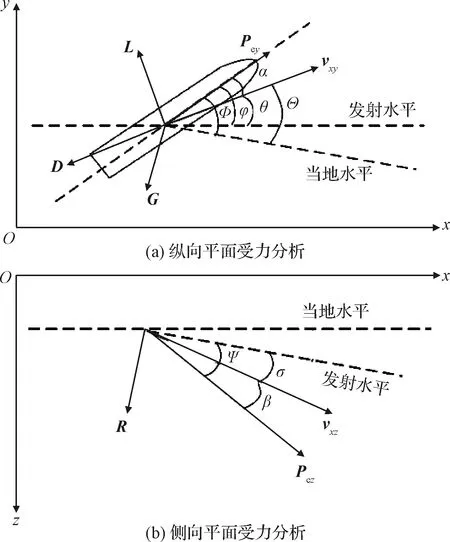
图1 上升段受力分析示意图Fig.1 Diagram of force analysis in ascending phase
为了简化计算,对模型进行了若干假设。第一,将SLV视为质点,忽略旋转。第二,不考虑摆动喷管的影响。第三,地球被视为一个球体。第四,忽略科氏力和离心力。第五,重力加速度为常值。基于上述假设,大气层内SLV上升段三维运动方程为
(1)
式中:h为高度;z为侧向位移;Pe和m分别表示发动机推力大小和SLV质量;g为重力加速度。
气动力的计算方式如下:
(2)
式中:cD,cL和cR分别为升力系数、阻力系数和侧向力系数;ρ为大气密度;Sm为气动有效面积。
1.2 约束条件
初始条件:根据上升段三维动力学模型(1),初始条件可表示为
(3)
过程约束:对于大气层内的上升段运动,SLV受过载、攻角和侧滑角变化率约束,以及动压约束。
其中,纵向平面和侧向平面的法向过载约束分别为
(4)
式中:nv和nh分别为纵向平面和侧向平面的法向过载;nvmax和nhmax分别为nv和nh允许最大值绝对值。
攻角侧滑角的变化率约束分别为
(5)
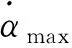
动压约束为
q=0.5ρv2≤qmax
(6)
式中:qmax为允许的最大动压值。
终端约束:包含终端高度、速度、终端当地弹道倾角、侧向位移约束以及当地弹道偏角约束
(7)
不确定性:SLV飞行过程中面临的主要不确定性来自于发动机参数,即发动机比冲和质量秒流量
(8)
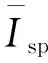
对于大气层内的飞行,除了式(8)中的不确定性外,还考虑气动系数不确定性。为了简化问题,本文只考虑cL和cD的不确定性:
(9)
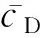
2 制导算法设计
R3DEM算法的制导方案示意图如图2所示,图中物理量的意义将在后文进行说明。R3DEM各部分功能如下:
在线参数辨识:根据加速度计的测量值,将ΔcD, ΔcL和Pe/m视作扩展状态量。通过对模型的合理简化,建立上升段参数辨识的近似模型。利用容积卡尔曼滤波对模型中的不确定性参数进行辨识,并实时修正模型参数。详细过程见3.1。
在线轨迹规划:实现轨迹的在线更新。构建攻角和剩余速度能力曲线的数学形式,将终端高度、速度、当弹道倾角、侧向位移和当地弹道偏角表示为关于曲线参数的代数方程。提出一种改进的侧向能量管理,在传统真空能量管理的基础上,考虑气动力的影响,分别给出发动机和气动力产生的剩余速度能力的计算方法。详细过程见3.3。
轨迹解算:采用牛顿法实时求解攻角参数和速度能力曲线,实现在线轨迹规划。详细过程见3.3。
过程约束:将动压、过载和控制量幅值及变化率约束转化为攻角曲线和侧向速度能力曲线的可行域。若在线轨迹规划得到的攻角曲线和侧向速度能力曲线在可行界内,则按照规划的路径飞行;否则,沿着可行域边界进行飞行,保证轨迹实时满足路径约束。详细过程见3.4。
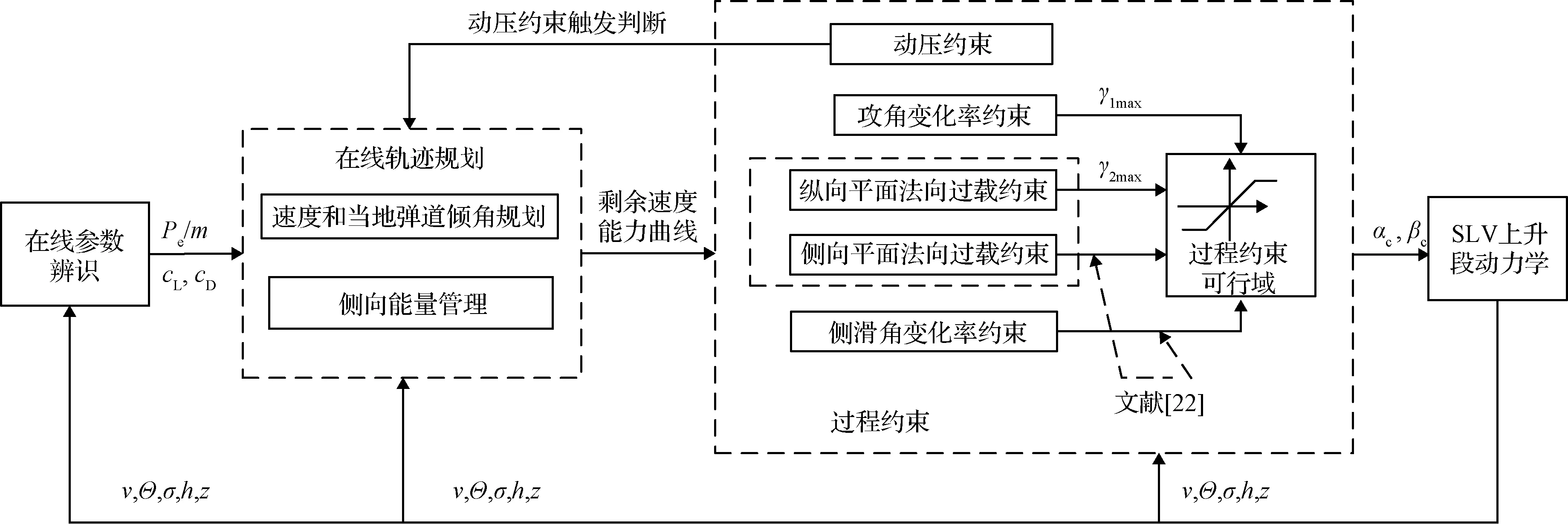
图2 制导方案示意图Fig.2 Diagram of the guidance scheme
2.1 基于容积卡尔曼滤波的参数在线辨识
由于大气层内上升段面临发动机参数和气动系数等多种不确定性,常用的扩张状态观测器[22]对所有不确定性的总体影响进行观测,无法将每种不确定性分开观测。因此,本文采用滤波方法对各参数不确定性进行辨识。参数辨识中常用的非线性滤波方法,如扩展卡尔曼滤波(Extended Kalman filter,EKF),是将非线性方程线性化处理。EKF算法需要计算扩展状态方程的雅可比矩阵,不但增加了计算量,且容易引起滤波发散[23]。相比之下,容积卡尔曼滤波(Cubature Kalman filter,CKF)通过三阶容积积分规则,利用容积点的加权对高斯积分进行逼近,可达到三阶Taylor展开的精度,具有较高的滤波稳定性[24]。

(10)
由于SLV在第二级时质量较大,有如下近似关系:
(11)
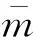
在实际飞行中,上升段动力学参数的摄动具有随机性,难以用精确的模型描述。为了简化问题,本节将参数摄动模型近似如下:
(12)
式中:δD,δL>0,为常数。
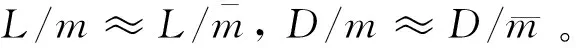
(13)
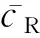
将待辨识的模型参数与原系统状态量合并,扩展成新的状态量。将式(1)和式(12)组合后,采用四阶龙格-库塔法则离散化,得到扩展后的状态方程:
xk=F(xk-1,uk-1)
(14)
式中:xk=[v,Θ,σ,h,z,ΔcD,ΔcL,ΔPe/m]T|t=k是系统在k时刻的状态向量;uk=[α,β]T|t=k是系统在k时刻的输入向量。
采用四阶龙格-库塔法则将式(13)离散化,得到观测方程:
zk=H(xk,uk)+wk
(15)
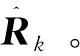
利用文献[24]中的容积卡尔曼滤波,对由式(14)和(15)构成的离散系统进行辨识,可实现对ΔPe/m, ΔcD和ΔcL的在线估计。
2.2 大气层内侧向能量管理的制导
2.2.1大气层内侧向能量管理的基本原理
大气层内能量管理的基本原理如图3所示。横轴和纵轴分别代表当地水平和当地侧向速度。vz和vf分别为当前时刻侧向速度矢量和终端时刻期望侧向速度矢量;Δvf为期望速度增量;DP和RP分别是阻力和侧向力在侧向平面推力方向上的分量;对于耗尽式关机的SLV,侧向平面内能量管理将发动机推力和气动力在侧向平面所提供的剩余速度能力进行耗散。VCAPz是侧向平面剩余速度能力,可以分解为VTCAPE(由发动机推力提供的剩余速度能力)、VACAPP和VACAPL(由气动力提供的剩余速度能力)。根据能量管理基本原理[22],有如下关系式:
(16)
式中:VTCAPz为侧向平面内,由发动机推力和侧向力共同产生的负荷剩余速度能力曲线。
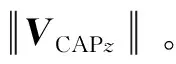

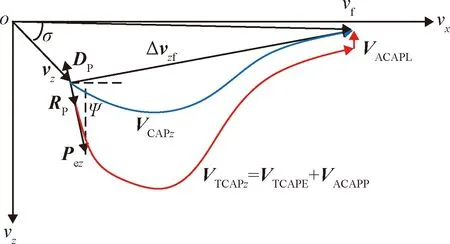
图3 侧向能量管理原理Fig.3 The principle of lateral energy management
注1.根据SLV在上升过程中的飞行特点,v在推力作用下增大。SLV在发射的过程中,姿态由垂直到水平,当地弹道倾角从90°降至0。因此,vx=vcosΘ是单调递增的,可以用来作为飞行过程的自变量。
2.2.2气动力的分解
传统的纵向平面大气层外能量管理分别计算推力和重力产生的剩余速度能力[16]。基于该思想,分别将D和R沿着侧向平面内发动机推力方向和当地侧向方向分解,如图4所示。DP,DL,RP和RL分别是D和R沿着这两个方向的分量。Dxoz表示阻力在当地水平面的分量。
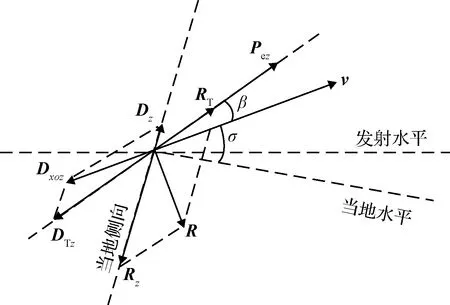
图4 侧向平面气动力分解Fig.4 Aerodynamic force decompositionin lateral plane
通过上述分解,可以得到R和D在侧向平面内,沿推力方向和当地侧向方向上的分量为
(17)
2.2.3剩余速度能力分量的计算

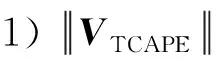
将积分变量由t替换为vx,则的表达式如下:
(18)
式中:M(vx)为质量关于vx的函数。
由于气动力远小于飞行第二阶段的推力且固体SLV采用耗尽式关机,可以得到以下近似关系:
(19)
由式(18)可知,在发动机剩余速度能力计算时,将Pe/M(vx)作为一个整体。可通过2.1节对Pe/m进行更新,获得较为精确的发动机剩余速度能力。

参考VTCAPE的计算方法,有:
(20)
式中:
(21)

2.2.4VTCAPz的起始点与终点
设VTCAPz的表达式为S(vx),则S(vx)当前时刻下的起始点为(vtcosΘtcosσt,vtcosΘtsinσt)
S(vtcosΘtcosσt)=vtcosΘtsinσt
(22)

(23)
为了保证终端当地偏航角Ψ=0,S(vx)在终点(vf,0)的导数为:
S′(vf)=0
(24)
当速度到达vf时,为了使推力和气动力在侧向平面的分量产生的剩余速度能力完全耗尽,有:
(25)
2.2.5侧向位移增量Δz计算
设A(vxA,S(vxA))和B(vxB,S(vxB))分别为VTCAPz上的两点。当速度沿着VTCAPz从A至B时,侧向位移ΔzA→B可以按照如下计算:
(26)
由于直接求取∂ΔzA→B/∂vx较为困难,可以将其写成导数乘积的形式:
(27)
在图1中,有如下近似关系:
β=Ψ-σ
(28)

(29)
将式(27)和(28)代入到式(1),有
(30)
因此,当速度向量沿着VTCAPz由A点运动到B点时,产生的侧向位移ΔzA→B为
ΔzA→B=
(31)
则从当前时刻到终端时刻,由VTCAPz和VACAPP共同引起的侧向位移Δz为
(32)
2.2.6高度增量和当地弹道倾角增量的计算
(33)
(34)
因此,Θ和h均可以表示成关于vx的方程:
(35)
终端高度和当地弹道倾角约束可表示为
(36)
由于终端高度和当地弹道倾角通过攻角进行控制,为了保证攻角解的唯一性,构造了一条包含两个待定参数的攻角曲线。假设SLV将在如下攻角的数学形式下进行剩余飞行:
α(vx)=γ1vx+γ2
(37)
式中:γ1和γ2是制导周期内需要求解的参数。
2.3 轨迹的解算
2.3.1约束代数方程的建立
由上述设计过程可知,VTCAPz=VTCAPE+VACAPP。根据式(36),(22)-(25)和(32),三维轨迹应满足:
(38)
由于SLV在终端时刻需要返回发射面,因此终端侧向位移为零,即Δzf=0。
注3.为了保证式(38)有唯一解,α(vx)和S(vx)中未知数的总数应该等于式(37)中的方程个数。由于α(vx)包含了2个未知数[γ1,γ2]T,S(vx)应包含5个未知数。有无穷多数学形式的S(vx)可以满足式(38)。对于该问题,多项式曲线有两个优点:首先,多项式函数的特点是它可以任意增加未知数的数目来匹配方程组的数目。其次,它的导数形式比较简单。因此,可用5阶多项式曲线来拟合S(vx):
S(vx)=A(vx-vxf)4+B(vx-vxf)3+C(vx-vxf)2+
D(vx-vxf)+E
(39)
通过将攻角和剩余速度能力曲线设计为特定的数学形式,将上升段能量管理制导问题转化为代数方程求解问题,进而在线获得制导指令。
2.3.2S(vx)和α(vx)参数计算
假设所有状态量都是可测的,则式(38)是关于[γ1,γ2,A,B,C,D,E]T的方程组。在式(38)中:
S(vf)=VACAPL,S′(vf)=0
(40)
显然有:
(41)
因此,式(38)可以化简为
(42)
设K=[K1,K2,K3,K4,K5]T,Π=[γ1,γ2,A,B,C]T。为了便于计算,采用Simpson法对积分进行近似。
注4.一些改进的数值迭代算法同样可以有效地解决本问题,兼顾计算效率和收敛性能,本文选择牛顿法进行迭代计算:
(43)
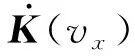
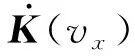
2.4 过程约束
本文考虑过载、和控制量变化率、控制量幅值以及动压约束约束。
注6.侧向平面法向过载约束和侧滑角的变化率约束可行域求解方法与文献[22]的相同,这里不再赘述。
2.4.1攻角变化率约束
根据导数分解原则,有
(44)
则
(45)
式中:
(46)
2.4.2纵向平面法向过载约束
纵向平面内的法向过载约束如下:
(47)
其边界情况分为:(a)α>0和(b)α<0。考虑到篇幅的限制,这里仅以α>0的情况为例进行说明。
根据式(47),当触发法向过载约束时满足:
cosΨmax1cosΦmax1sinΘt+D
(48)
设υ=sinΦmax,则式(48)可以写作:
S2(vxt))cLSm
(49)
对式(49)进行牛顿迭代,可以获得υ1:
υ(k-1)
(50)
式中:υ(k-1)和υk分别表示相邻两次牛顿迭代的υ值。
根据式(44),有:
|Φ|=|γ1vx+γ2+Θt|<|γ1vx+Θt|+|γ2|=
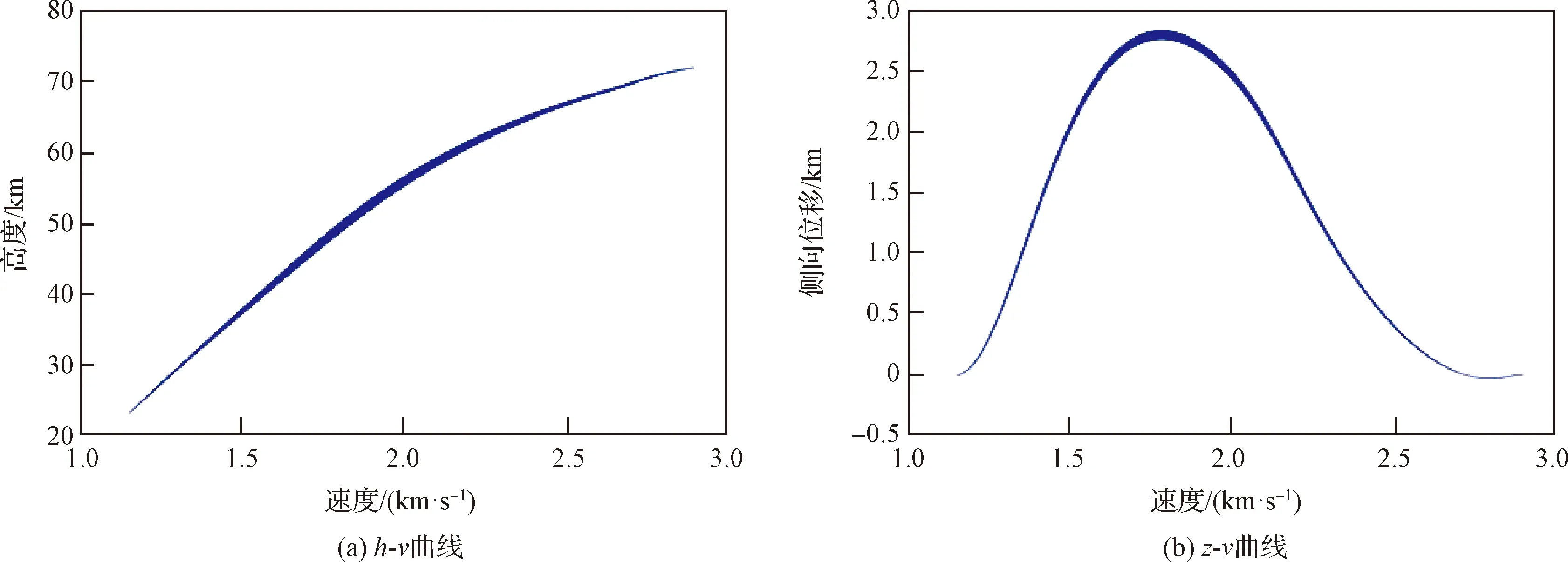
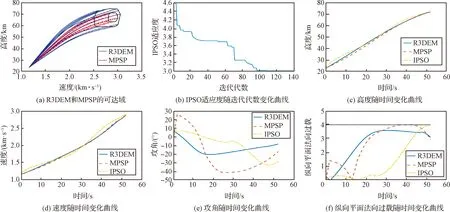
γ2 (51) 因此,有: |γ2| (52) 由此可以得出,纵向平面内的法向过载约束对|γ2|施加了限制。 2.4.3动压约束 大气层内能量管理不但要考虑过载约束、攻角和侧滑角的幅值、变化率约束,还要满足动压约束。由于侧向位移相对高度而言较小,近似认为动压只与高度和速度有关。假设大气密度随高度变化如下: ρ(h)=ρ0e-ζh (53) 式中:ρ0是零海拔处的大气密度;ζ>0为常数。 根据式(53),需要实时满足: (54) 定义动压约束触发判断方程(55)。第一项表示在某一速度vxt+τ时,触发最大动压约束qmax的最低临界高度。第二项表示速度为vxt+τ时的预测高度。这里,τ=(vfcos Θf-vxt)/100是关于vx的积分步长。当预测高度高于临界高度时,不违反动压约束。 h(vxt+τ) (55) 若Jq>0,则说明当vx=vxt+τ时,动压超出约束值qmax。此时,对式(42)中的K5(vx)进行替换,使得vx=vxt+τ时满足动压约束: (56) 式中: (57) 另一方面,若当前时刻Jq<0,则K5(vx)保持不变。 本节通过仿真校验来验证R3DEM算法的有效性。首先,给出仿真的初始条件。然后,验证该算法在不同任务中的适用性,以及在含有模型参数不确定性情况下的鲁棒性。最后,通过与模型预测静态规划算法和改进粒子群优化算法的比较,验证算法的优越性。 本文的研究背景是三级SLV的第二级,表1给出了制导任务满足的部分约束条件。 表1 初始条件、终端约束和路径约束Table 1 Initial, terminal and path constraints 为了验证R3DEM算法的适应性,对终端高度63000~72000 m,终端速度2550~3000 m/s下的四种制导任务进行测试。终端当地弹道倾角设置为6.5°。 4种终端高度和终端速度下的仿真结果如图5所示。图5(a)和(c)为h-v曲线和当地弹道倾角随时间变化曲线。可以得出,R3DEM算法可以满足4种不同任务下的终端状态约束。图5(e)为攻角随时间变化曲线。由图5(d)中当地弹道偏角随时间变化曲线可知,当速度达到终端约束值时,当地弹道偏角收敛至0。由图5(b)中的z-v曲线可知,侧向位移z在终端时刻收敛至0,这表明SLV最终回到了发射平面。此外,图5(b)中侧向位移变化率收敛至0,图5(d)中终端当地弹道偏角收敛至0,二者均表明终端时刻侧向速度收敛至0。终端侧滑角收敛至0,表示速度方向与弹体体轴方向重合,体轴调整到发射平面,满足了第三级助推的起始条件。图5(f)表明,为了达到精确控制速度的目的,在侧向平面内机动消耗了多余的能量,且终端高度和速度越小,需要消耗的发动机能量越多。图5(g)和(h)分别为纵向平面法向过载绝对值和侧向平面法向过载绝对值随时间变化曲线。图5(i)为动压随时间变化曲线。第二级飞行过程始终满足所有的过程约束,且触发了过程约束的边界条件。尽管如此,由于速度能力曲线始终在其可行域内,因此约束始终没有超出边界值。 图5 不同高度、速度任务下的仿真结果Fig.5 Simulation results for various combinations of altitude and velocity 图6(a)和(b)分别为蒙特卡洛仿真试验下,h-v和z-v的包络线。所有轨迹均满足终端高度、速度和当地弹道倾角约束,且摄动轨迹均在标称情况附近。终端高度、速度、当地弹道倾角最大误差值分别为13.3 m, 5.44 m/s, 0.013°,满足精度指标要求。 图6 含有不确定性的蒙特卡洛仿真结果Fig.6 Monte Carlo simulation results with uncertainty 为了检验R3DEM的速度调节能力,分别给出了R3DEM和MPSP算法的终端可达区域。由图7(a)可知,R3DEM的可达区域完全覆盖了MPSP。因此,与MPSP相比,R3DEM具有更强的终端适应能力。IPSO适应度随迭代代数的变化曲线如图7(b)所示。IPSO经过120次迭代后收敛,得到最优解,平均收敛时间超过5 min,这显然不适用于在线制导。相比之下,R3DEM仅需10 s左右。图7(c)和(d)分别为高度和速度随时间变化曲线,三种算法都可以达到期望的终端速度和高度。由图7(e)可知,MPSP产生的攻角大于R3DEM和IPSO。R3DEM和IPSO算法在纵、侧向两个平面对速度进行耗散,因此产生的攻角和侧滑角较小。由于MPSP的速度耗散完全依赖于纵向平面,导致了大范围的攻角变化,进而产生图7(f)中较大的法向过载。过载约束是制约速度调节能力的重要因素,MPSP算法触发过载约束的时间较长,导致其速度调节能力较低。R3DEM和IPSO算法的过载在整个过程中都处于约束值之下。 图7 R3DEM,MPSP,IPSO的仿真结果对比Fig.7 Simulation results comparison among R3DEM, MPSP and IPSO 本文提出了一种基于能量管理的三维在线轨迹规划制导算法,仿真结果表明,该算法适用于耗尽关机的SLV大气层内上升段。本文的主要结论如下: 1) 提出了一种SLV上升段制导算法,将求解空间轨迹曲线的问题转化为求解攻角和速度能力曲线参数的问题,能以较高的精度满足终端约束。 2) 本文提出的制导算法将传统的纵向平面制导扩展到三维空间,扩大了终端速度的可调范围。当终端在纵向平面上达到规定的高度和速度时,其侧向位移和速度收敛至零。与模型预测静态规划方法相比,拓宽了终端速度调整范围。与改进的粒子群算法相比,计算效率得到了提高。 3) 可在过载、动压和控制量变化率约束,以及模型参数不确定性情况下,能以较高精度完成制导任务。3 仿真校验
3.1 仿真条件

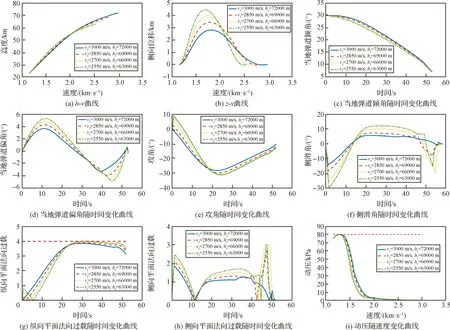
3.2 适应性验证
3.3 鲁棒性验证
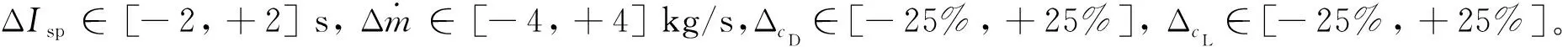
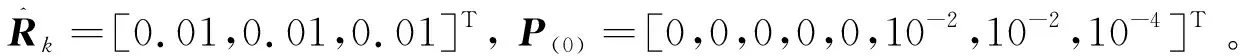
3.4 与现有方法比较

4 结 论
