机动发射弹道导弹集群诸元快速规划

臧红岩，高长生，荆武兴

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引 言

弹道导弹作为现代战争中的重要武器系统之一，其作战反应能力能够直接影响战争格局，但近年来随着各国导弹防御系统的发展，弹道导弹的生存、打击能力受到了严重威胁。传统的单枚弹道导弹作战模式已经无法满足日益复杂的任务需求，而弹道导弹集群作战能够有效提升打击精度，增强突防能力，弹道导弹集群作战已经成为一种新趋势。目前，导弹集群作战的研究主要集中于导弹、无人机等强机动性飞行器的轨迹、制导、控制、协同打击等方面，针对弹道导弹集群机动发射的相关研究较少[1-5]。而作为导弹体系作战中最重要的一环，弹道导弹集群的发射对机动性、快速性提出了更高的要求，即需要在满足打击精度的条件下，在较短的反应时间内完成多枚弹道导弹的发射诸元装订。

导弹发射诸元装订包括诸元规划和装订上弹两部分工作[6]。其中诸元规划过程对于弹道导弹作战反应能力、射前生存能力有较大影响，与导弹型号、制导控制算法等有着紧密的联系，目前已经有学者在发射诸元的选取、解算、规划方法等方面展开了研究。导弹发射诸元规划方法主要包括解析法、数值法以及智能算法。文献[7-8]采用解析法，考虑导弹主动段飞行程序和弹道特性，通过多项式拟合建立发射诸元的解析模型，并将得到的诸元作为初值进行迭代求解，实现了发射诸元的快速规划，但解析表达式求取困难，精度有待提升;而数值法计算精度高，但实时性较差。文献[9-11]考虑飞行器助推段的各种约束作用，通过将直接法、间接法等优化算法相结合，构造新的迭代算法求解得到发射诸元，但计算过程比较复杂，无法满足机动发射需求。文献[12]以助推滑翔飞行器为研究对象，将中心弹道诸元作为迭代初值，引入松弛因子，采取部分诸元迭代结算模式，在一定程度上降低了诸元规划时间。随着智能方法的发展，神经网络为发射诸元快速规划提供了新的解决方案，神经网络具有较强的数据拟合能力，可以应用于学习复杂的映射关系。文献[13]将神经网络运用于对运载火箭剩余运载能力的估计，并对程序角进行了在线重构。文献[14]针对潜地导弹，利用BP神经网路对导弹落点参数进行快速计算。文献[15]基于神经网络提出了一种基于监督学习的在线预测方法，用于对弹道导弹中段突防中的拦截点坐标及拦截时间进行预测。文献[16]基于神经网络建立发射初始条件、飞行程序到关机点状态信息的映射关系，结合优化算法对助推滑翔飞行器诸元进行了快速规划;但智能方法也存在一些缺陷，比如制备大量数据耗时长，过于依赖数据库可能导致算法稳定性差等。

综上，本文以弹道导弹为研究对象，针对集群机动快速发射需求，将神经网络与传统优化方法相结合开展工作。首先，分析了弹道导弹助推段飞行策略并选取发射诸元，基于BP神经网络方法设计了双隐藏层诸元预测网络，并利用建立的样本数据库对网络进行训练，可快速给出一定范围内任意发落点对应的发射诸元近似值。然后，将诸元预测网络得到的发射诸元作为初值，将落点射程、横程及高程偏差最小作为目标函数，采用最小二乘优化方法对发射诸元进行迭代，得到诸元精确解。最后，建立了典型场景下的弹道导弹集群机动发射诸元快速规划仿真。结果表明，本文的方法结合了智能方法和传统优化方法的优点，弥补了智能方法依赖数据库的缺陷，提高了算法稳定性，同时减少了优化迭代次数，能够有效提升发射诸元规划的速度和精度，能够实现机动发射条件下弹道导弹集群的发射诸元快速规划。

1 弹道导弹诸元规划模型

1.1 数学模型

机动发射弹道导弹运动模型基于六自由度弹道仿真模型建立，考虑地球自转，将地球视为标准椭球。导弹在助推段飞行过程中，主要受重力、发动机推力、空气动力、控制力以及它们产生相应力矩作用，忽略级间分离带来的干扰作用，其质心运动数学模型在发射系下可以表示为[17]：

(1)

式中：r为地心到导弹当前位置的矢量；m为导弹的当前质量；g为投影于发射坐标系中的引力加速度；Fe为地球自转引起的牵连惯性力；Fc为地球自转引起的科氏惯性力；v为导弹在发射坐标系下的速度矢量；Γ01为发射坐标系到弹体坐标系的转换矩阵；Γ03为发射坐标系到速度坐标系的转换矩阵；Isp为发动机比冲；R为投影于速度系中的空气动力矢量；P为投影于弹体坐标系中的发动机推力矢量；P为发动机推力大小。

1.2 助推段飞行策略

多级弹道导弹助推段飞行模式可分为连续助推、连续助推+滑行(末段修正)、间隔助推，本文中选取连续助推模式。对于机动发射弹道导弹，在给定发射点位置、方位角信息以及俯仰角飞行程序后，便可得到一条唯一的弹道,控制导弹飞向目标。根据导弹助推段飞行特性，将弹道导弹助推段分为垂直上升段、转弯段和瞄准段。实际工程中经常选取俯仰角特征参数作为控制量进行弹道设计，同时还会将方位角信息考虑在内。弹道导弹助推段俯仰角变化如图1所示。

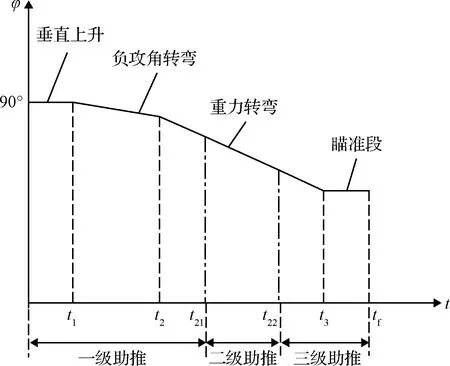
图1 弹道导弹助推段俯仰角飞行程序Fig.1 Flight procedure of pitch angle in the boost phase of ballistic missile

本文中设定俯仰角飞行程序为：

(2)

式中：θ为弹道倾角，αm为瞄准段攻角，本文中取常值；α(t)为负攻角转弯段攻角变化规律，负攻角转弯段根据要求应在达到气动力急剧变化的跨音速之前结束，以减少气动载荷和气动干扰。故可在马赫数Ma=0.8～1.2时，使攻角收缩为零，变化规律如下：

(3)

式中：αx为亚音速段上攻角绝对值的最大值，称为限制攻角；v为导弹当前速度大小；vf为攻角收缩为零时的速度(一般Ma为0.8～1.2)；v0为垂直转弯结束时刻的速度；v1,v2为中间节点时刻速度，计算公式如下：

(4)

式中：c为常数，决定了攻角由0下降至-αx及由-αx上升至0的时间，本文中取为0.1。由式(3)所描述的攻角变化规律如图2所示。

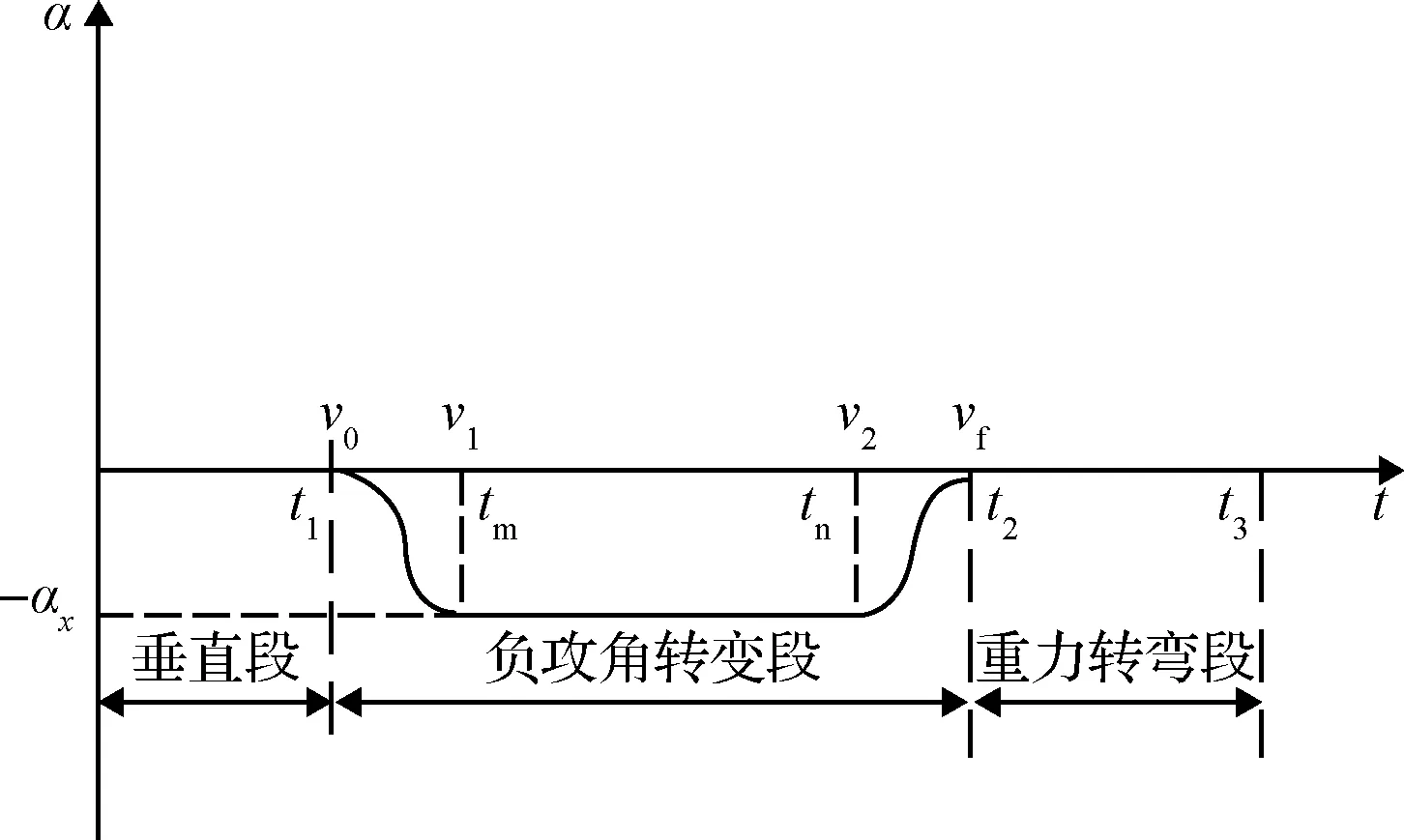
图2 攻角变化规律曲线Fig.2 Variation of the angle of attack

图中横轴为时间，纵轴为攻角。

1.3 诸元规划输入参数分析

通过对于导弹质心运动模型的推导，确定弹道轨迹信息的参数主要有：(1)发落参数：包括发射点经度λF、纬度BF、高度HF和目标点经度λM、纬度BM、高度HM；(2)主动段飞行程序参数：包括发射方位角A0、垂直上升段飞行时间t1、负攻角转弯段最大限制攻角αx、负攻角转弯段结束时刻速度vf，重力转弯段结束时刻t3以及瞄准段瞄准攻角αm。

在导弹发射之前，可以第一时间得到的信息是导弹的发落参数，因此将导弹的发落参数作为诸元规划模型的输入参数。主动段飞行程序参数中,垂直上升段飞行时间t1根据导弹型号不同而有所区别;负攻角转弯段结束时刻速度vf本文中取Ma=0.8;重力转弯段结束时刻t3取导弹燃料剩余60%的时刻，才可以保证后续瞄准段完成对于目标的瞄准。因此本文中对于弹道起主要作用的参数选取为发射方位角A0、负攻角转弯段最大限制攻角αx以及瞄准段瞄准攻角αm。

1.4 诸元规划模型

通过上述分析，导弹诸元规划模型的输入参数为：发射点经度λF、纬度BF、高度HF和目标点经度λM、纬度BM、高度HM共6个参数。模型的输出值为发射方位角A0、负攻角转弯段最大限制攻角αx以及瞄准段瞄准攻角αm，属于六输入三输出模型。如图3所示。

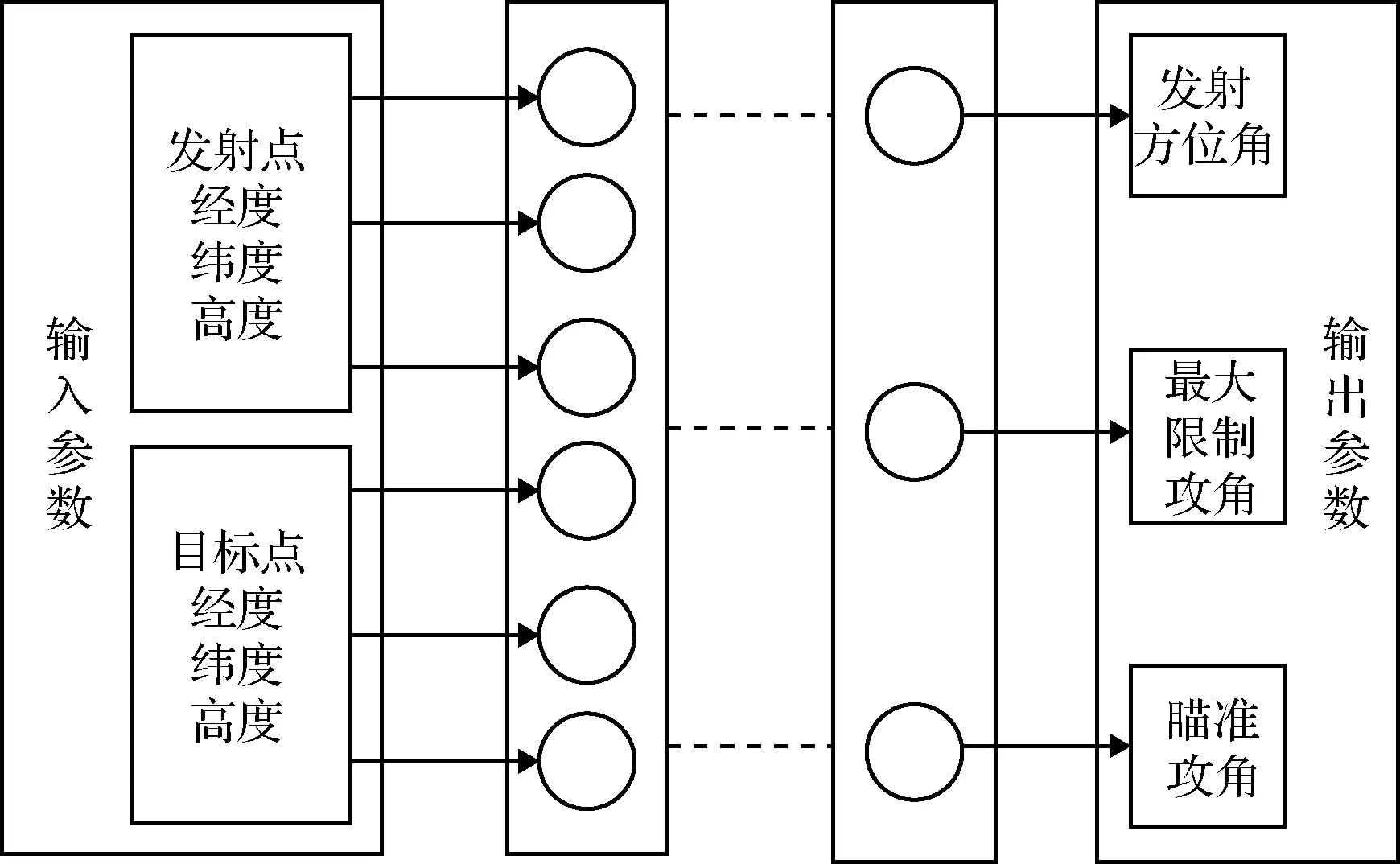
图3 诸元规划模型示意图Fig.3 Schematic diagram of the data planning model

2 诸元快速规划方法

2.1 诸元预测网络结构

BP(back propagation)神经网络又称为误差反向传播神经网络，是一种多层前馈网络。BP神经网络通过信号的前向传播和误差的反向传播来实现对于输入输出之间的映射关系的学习，由输入层、隐含层和输出层组成，层与层之间采用全连接方式，同层之间不存在相互连接，可以包含多个隐含层[18]。

本文将隐藏层数量设计为两层，如图4所示，结构为输入层-隐藏层1-隐藏层2-输出层。输入为发射点和目标点参数(λF,BF,HF,λM,BM,HM)，输出为选定的发射诸元(A0,αx,αm)。在进行神经网络的训练时，神经网络中的参数分为两类，一类是可以通过学习的方式进行更新的参数，如神经元之间的权值ω以及神经元的偏置b；另一类是不能通过学习的方式进行更新的参数，称之为超参数，如各层之间神经元节点数、隐藏层层数以及学习率等[13]。本文中超参数通过多次仿真确定，最后得到隐藏层1节点数为60，隐藏层2节点数为18。

图4 诸元预测网络结构图Fig.4 Structure diagram of data prediction network

2.2 样本集生成与处理

在进行神经网络的训练时，输入输出之间的关系越复杂，所需要的样本数据就越多，同时还要保证样本数据的随机性与均衡性。本文选取不同发射点和目标点情况下的最优弹道，作为样本弹道。以某型机动发射的洲际弹道导弹作为研究对象，导弹的发射点和目标点采用均匀分布随机生成，发射点经度范围为东经73°至东经135°，纬度范围为北纬3°至北纬53°，高度范围为0～1000 m，目标点经度范围为西经70°至西经130°，纬度范围为北纬25°至北纬49°，高度范围为0～1000 m。同时考虑到该型号导弹的实际战术技术指标，将射程控制在5000～12000 km范围内，通过求解弹道微分方程规划发射诸元，得到共计10000个样本，选取70%作为训练集，15%作为测试集，15%作为验证集。

根据样本数据的特点，为保证对于损失函数和梯度下降的计算，通常需要对其进行过归一化处理，将数据映射到[-1, 1]区间上，计算公式如下：

(5)

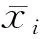
2.3 神经网络训练

在进行神经网络训练时，还需要确定损失函数、训练算法和激活函数。

1)损失函数的确定

损失函数用来表示预测值与真实值之间的误差，本文选取均方误差(MSE)作为损失函数，计算公式如下：

(6)

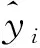
2)训练算法的确定

标准BP神经网络采用梯度下降算法，通过反向传播算法计算梯度，但由于其自身存在一些不足，样本数量较大时训练速度也有所下降，以及易于局部最小值时收敛等。本文采用LM(Levenberg-Marquardt)算法进行神经网络的训练。当误差性能函数具有平方和误差的形式时，Hessian矩阵可以近似表示为

H=JTJ

(7)

此时梯度的计算公式为

g=JTe

(8)

式中：J是雅可比矩阵，其元素由神经网络误差对权值和阈值的一阶导数组成；e是网络的误差向量。LM算法对上述近似Hessian矩阵按照下式进行修正：

x(k+1)=x(k)-[JTJ+μI]-1JTe

(9)

在神经网络训练过程中，当网络的误差减小时，减小μ值，当网络的误差增大时，增大μ值，保证网络性能函数始终减小。

3)激活函数的确定

激活函数是BP神经网络的重要组成部分。本文中隐藏层采用Tan-Sigmoid传输函数，也称为双曲正切S型函数，计算公式为

(10)

其曲线如图5所示。

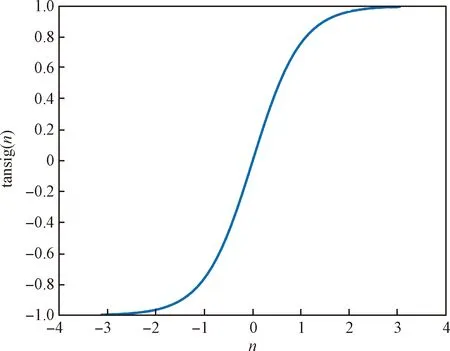
图5 双曲正切S型函数曲线Fig.5 Hyperbolic tangent S-type function

输出层采用线性激活函数。最大训练次数由网络规模，样本数量确定，经仿真验证，设定最大训练次数为1000，网络训练要求的精度设置为1e-3。

2.4 神经网络训练结果

图6～图7分别展示了诸元预测神经网络的训练过程和线性回归结果。图7中回归值R=0.99961。将测试数据集的输入参数代入神经网络，对比神经网络模型的预测输出结果与实际数据，得到方位角、限制攻角与瞄准攻角的残差如图8～图10所示。

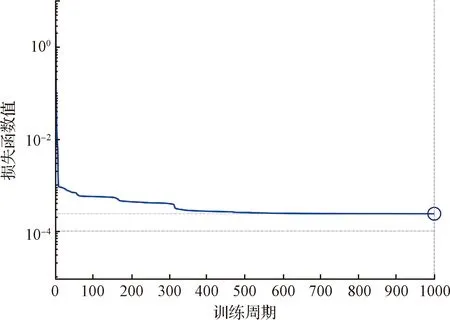
图6 网络误差性能曲线Fig.6 Network error performance

图7 线性回归结果Fig.7 Linear regression results

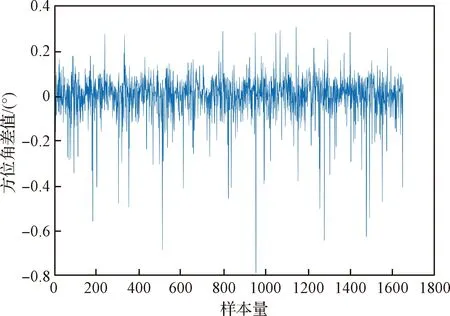
图8 方位角预测残差图Fig.8 Azimuth prediction residual diagram

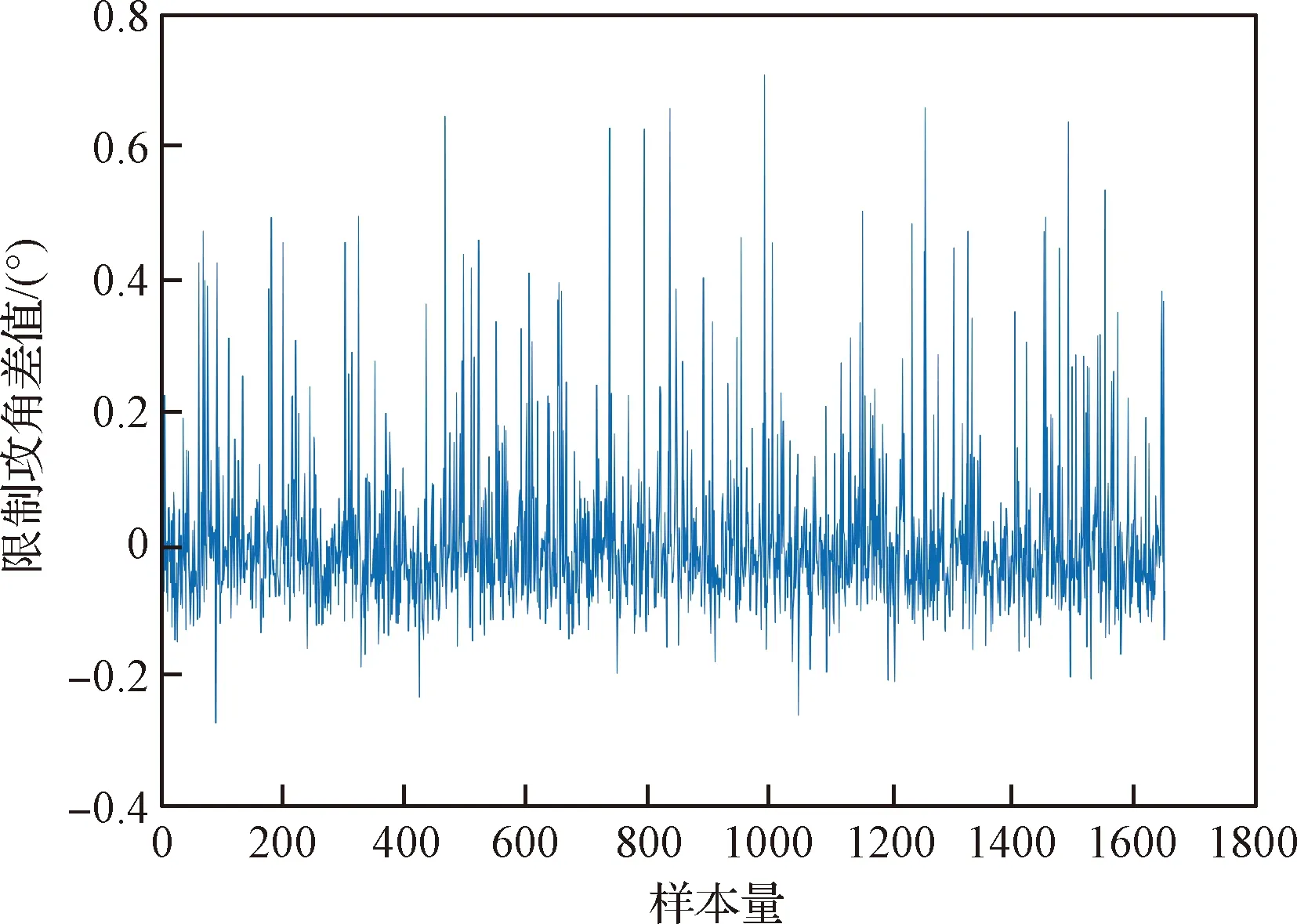
图9 限制攻角预测残差图Fig.9 Limited angle of attack prediction residual diagram

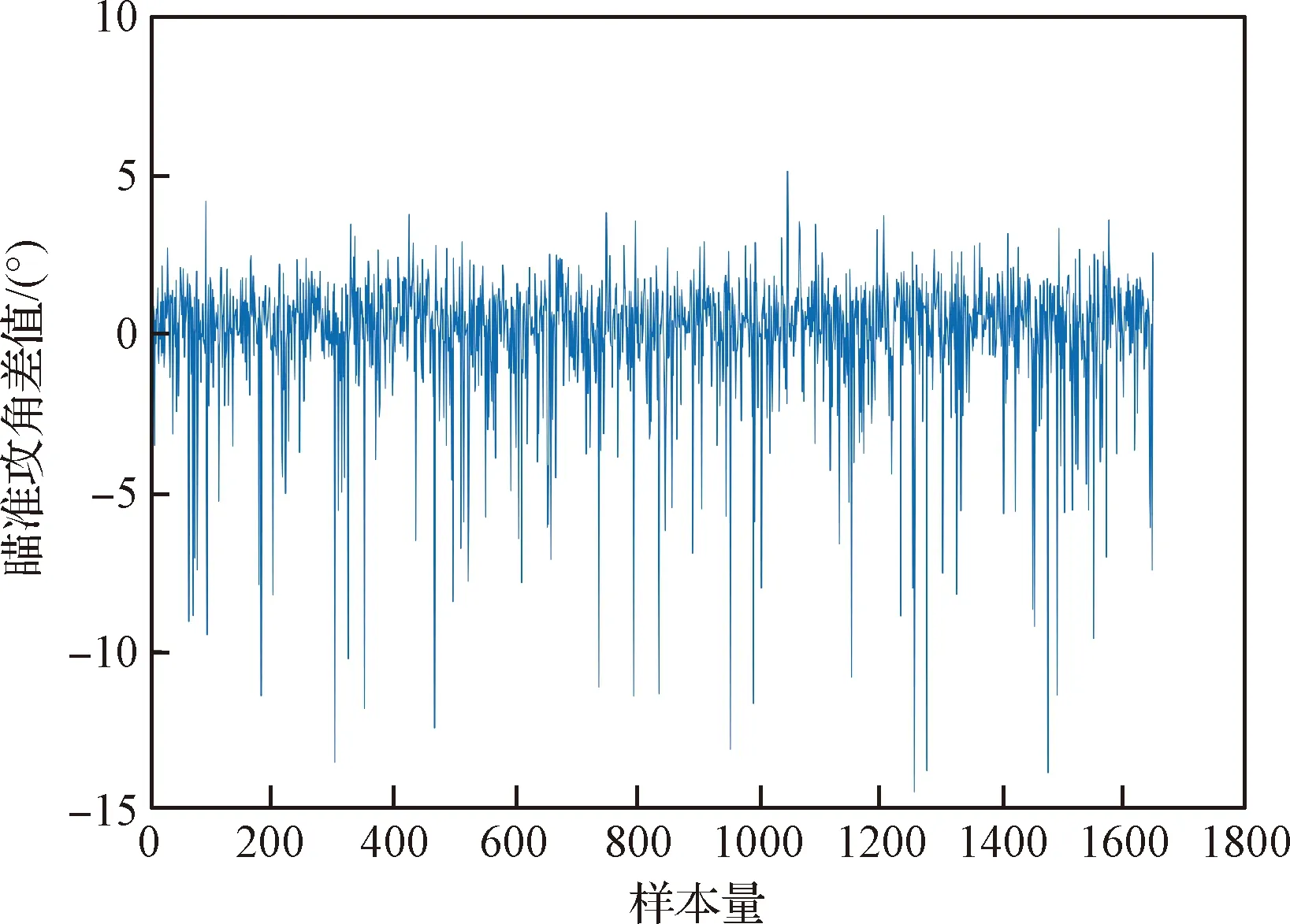
图10 瞄准攻角预测残差图Fig.10 Aiming angle of attack prediction residual diagram

从训练过程及残差图可以看出，训练的神经网络能够适应发落点经纬度及高度的变化，模型误差较小，较好地拟合了诸元规划过程。对于瞄准攻角，由于训练数据存在不平衡的特性，导致训练结果存在一定偏差,将采用下一节的方法对诸元进行修正。

3 诸元修正

本文采用最小二乘优化方法对双隐藏层神经网络得到的诸元初值进行修正，具体算法如下：当发射点为O(λF,BF,HF)，目标点为T(λM,BM,HM)，可以计算得到目标点的卯酉半径N：

(11)

式中：e=0.006694379990141为地球偏心率；Ra为地球赤道半径，则目标点在地固系下坐标为

(12)

发射点在地固系下坐标为

(13)

可得到地固系下发射点到目标点的矢径和横程距离为

(14)

运用训练好的神经网络可以得到一组诸元初值(A0,αx0,αm0)，将其代入动力学方程进行积分，得到落点射程lT，落点在发射系的坐标(XT,YT,ZT)。选取参数X=(A0,αx,αm)为自变量，目标函数为使下式的值最小：

J=GT(X)G(X)

(15)

式中：G(X)为差值函数，表示为

(16)

式中：Δl=lT-l0为射程偏差；ΔZ=ZT-ZM为横程偏差；ΔH=YT-HM为落点高度偏差。问题转换为寻找X变量值，使得式(15)性能指标最小，即：

(17)

由于G(X)具有很强的非线性，将其在X0处进行泰勒级数展开：

(18)

式中：∘(X)是高阶项。由上两式可以得到新的初值

X=X0-A-1B

(19)

式中：X0,A,B分别满足

(20)

将两式改写成迭代形式为：

(21)

式中：A,B满足

(22)

为了计算速度，不会让差值G(X0)减到零，假设控制精度ε，当满足如下条件时停止迭代

(23)

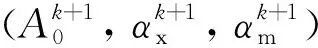
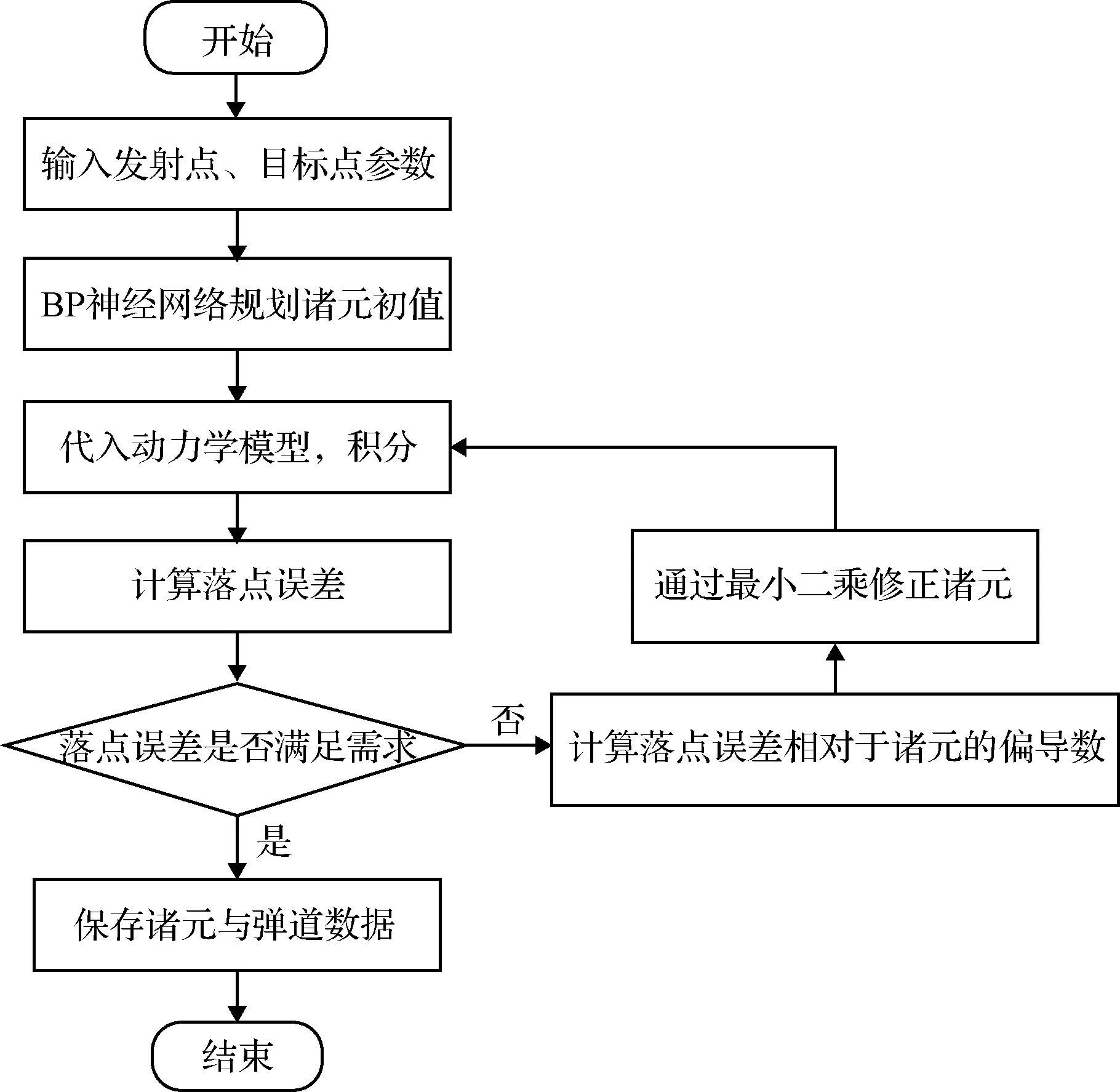
图11 诸元规划流程Fig.11 Flow chart of the data planning

4 仿真结果及分析

4.1 诸元快速规划仿真校验

选取某型机动发射的洲际弹道导弹模型，对前述诸元快速规划算法进行仿真验证。机动发射区域选取为将东经73°至东经135°，北纬3°至53°，将西经140°至170°，北纬25°至49°的区域作为打击目标范围。为验证本文提出的方法在所选取发落点范围内的有效性、快速性，在所选取的发落点范围内随机生成1000组发落点数据，分别采用基于BP神经网络的诸元规划快速方法、基于传统射表迭代以及基于解析-迭代优化的方法[8]求解发射诸元，来对比诸元快速规划结果。

通过对于1000组发落点数据进行诸元规划得到相应弹道数据，采用上述三种方法得到的仿真结果如表1所示：

表1 不同诸元规划方法仿真结果比较Table 1 Comparison of simulation results of different data planning methods

由上表可知，在精度一致时，相比于传统射表迭代求解诸元的方法，本文所提出的基于神经网络预测模型的弹道导弹发射诸元快速规划方法迭代次数有所减少，计算速度得到了显著提升。而解析-迭代优化求解诸元的方法虽然迭代次数更少，但由于计算复杂，迭代初值选取困难，导致其耗时更长。因此，本文提出的方法具有良好的工程应用价值，下面将进行弹道导弹集群机动快速发射的仿真校验。

4.2 弹道导弹集群机动快速发射仿真校验

为验证本文提出的方法对于弹道导弹集群机动发射条件下的适用性，在所选取的发落点范围内，进行弹道导弹集群机动发射仿真，仿真流程如图12所示，其中初始参数包括发射点机动范围、打击目标范围、导弹集群数量以及导弹参数等。

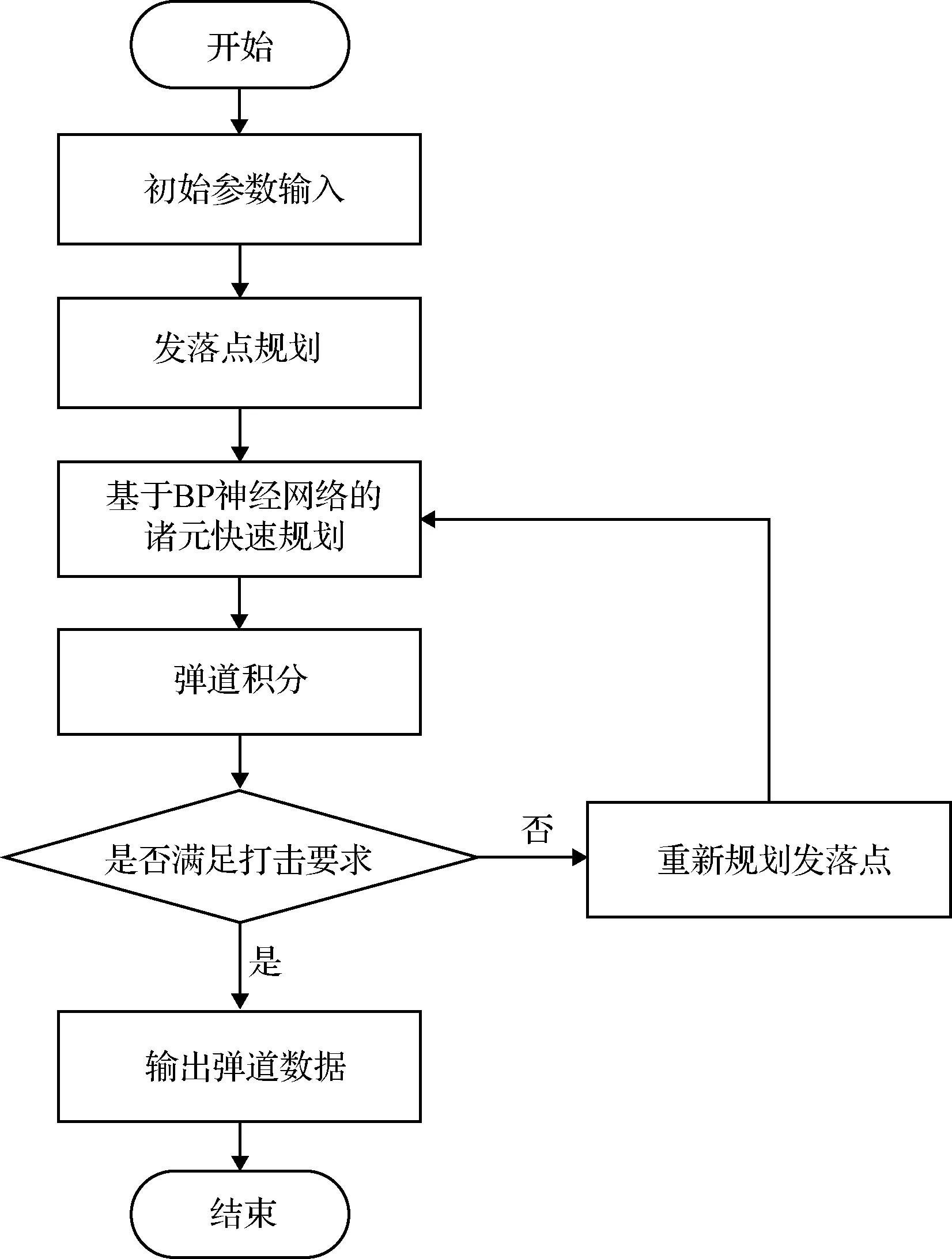
图12 机动条件下弹道导弹集群发射流程图Fig.12 Flow chart of ballistic missile cluster launch under maneuvering conditions

进一步缩小机动发射区域为将东经73°至东经83°，北纬3°至13°，打击目标范围缩小为西经160°至170°，北纬25°至35°，导弹集群数量选取为10枚，采用本文提出的基于BP神经网络的诸元快速规划方法对导弹集群发射诸元进行规划，仿真结果如图13～图16所示。

图13 导弹集群发射三维弹道Fig.13 Three-dimensional trajectory of the missile cluster

图14 导弹集群发射经纬度变化曲线Fig.14 Longitude and latitude changes of the missile cluster

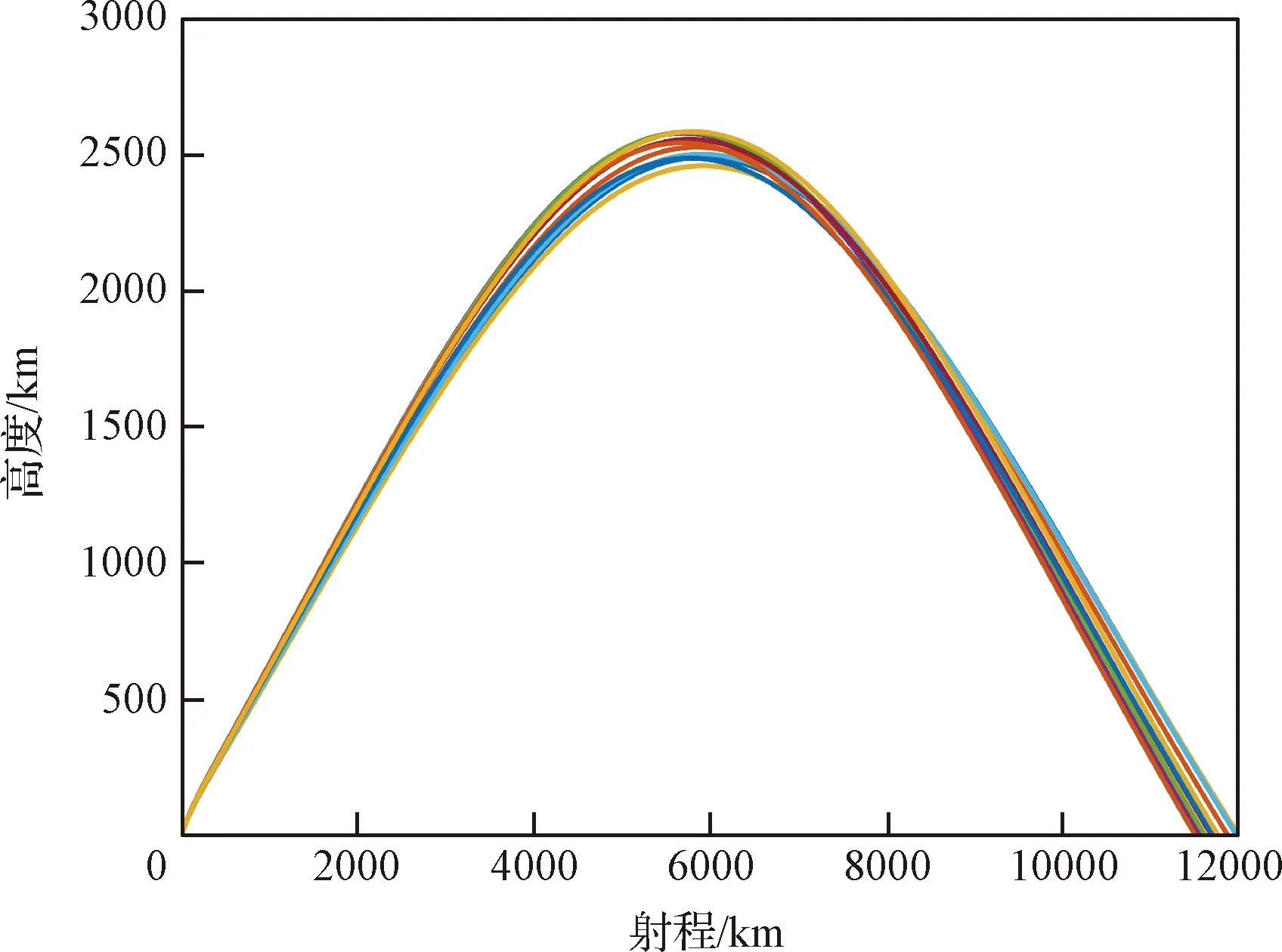
图15 导弹集群发射射程-高度曲线Fig.15 Variation of range versus altitude of the the missile cluster

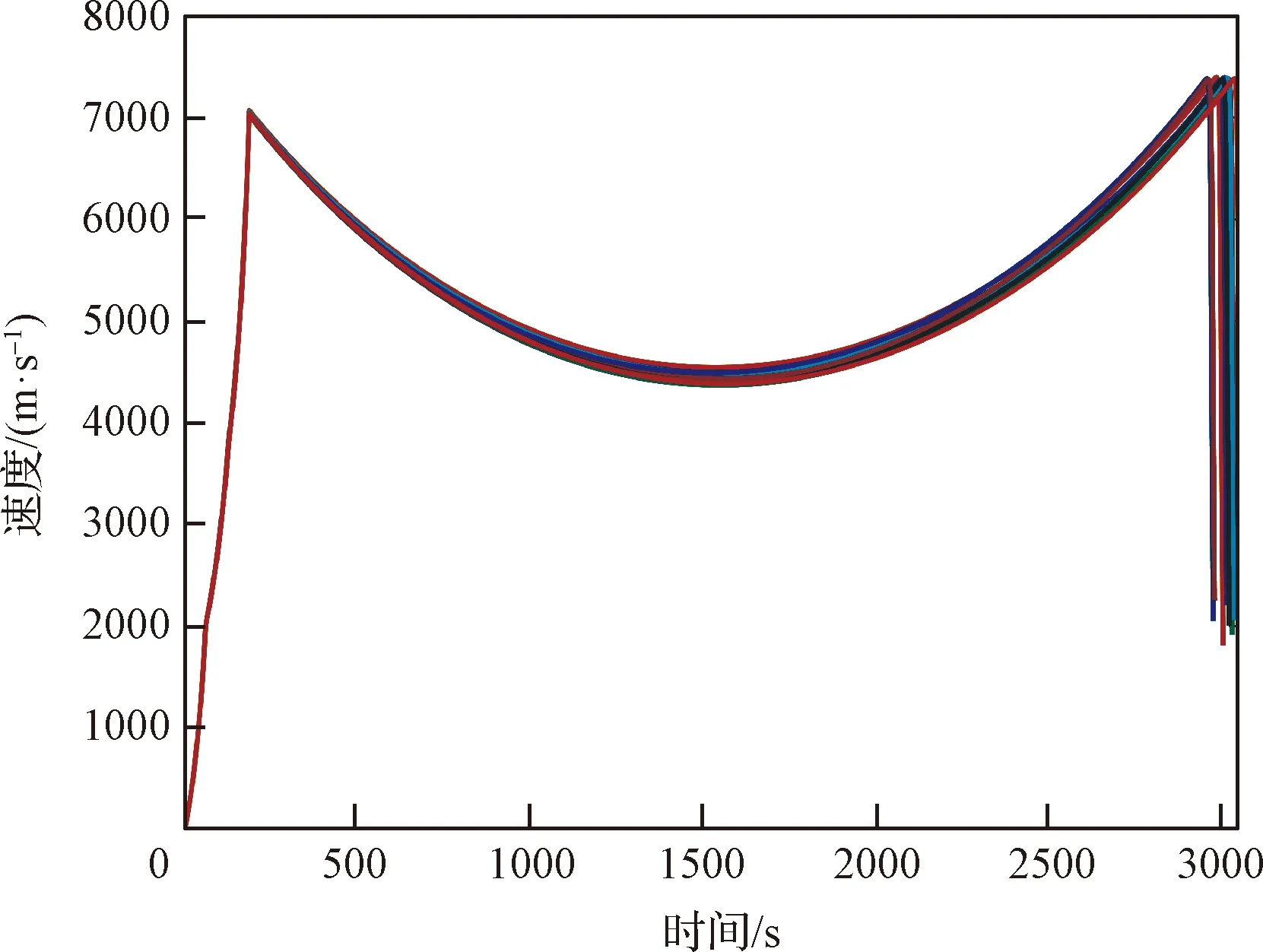
图16 导弹集群发射速度变化曲线Fig.16 Launch speed variation of the missile cluster

仿真结果表明，利用本文所提出的方法，能够满足弹道导弹集群在大范围机动条件下快速发射的需求，并且弹道在空间中分布范围较大，提高了相应突防效能，在战场实战环境下具有重大的应用价值。

5 结 论

本文针对弹道导弹集群机动快速发射的诸元规划问题，在飞行程序参数化的基础上，基于神经网络预测模型构建了发落点信息与发射诸元的非线性映射关系；针对训练样本数据不平衡导致的训练结果偏差，将双隐藏层神经网络与最小二乘优化算法相结合设计了一种发射诸元快速规划算法，实现了机动发射条件下的弹道导弹集群发射诸元快速规划。结果表明，BP神经网络诸元预测模型能够得到诸元近似解，并且在与最小二乘优化方法结合后效果较好，弥补了智能算法依赖训练样本数据的缺陷，对发落点经纬高变化适应性强，规划结果满足要求，并且在计算速度上得到了显著提升。同时，本文中提出的方法具有通用性，经扩展后能够满足多种型号、多种射程弹道导弹集群快速机动发射需求。