空间大质量目标转位操作双臂协调控制方法

刘 磊，张 涛

(1. 清华大学自动化系，北京 100084；2. 空间智能控制技术重点实验室，北京 100094)

0 引 言

根据公开资料，目前国内外大多数在轨航天器都没有进行可维修设计，其在轨寿命取决于发射前在地面上采取的一系列提高可靠性的措施，如采用成熟技术、冗余设计等。然而，航天器长期在轨运行，空间环境复杂，器件失效、部件老化、推进剂耗尽以及其它意外情况的发生，导致航天器发生故障难以避免[1]。航天器的故障危害大，损失严重，特别是对高价值航天器更是如此。空间高价值目标携带较多载荷，通常质量、惯量较大，尺寸较大。由于机械臂的臂展有限，为了使空间高价值目标上的待维修部位处于机械臂工作空间内，需要对目标进行转位操作。对空间高价值大质量目标进行双臂协调转位是在轨服务的一项常规操作。空间机械臂与大质量目标在转位过程中形成的时变动力学系统具有漂浮基、变质心、大负载等特性。从任务能力看，在对空间大质量目标进行在轨服务与维护操作时，采用双臂/多臂配置具有以下优势：①更强的搬运能力，可闭链工作；②更多的约束自由度，使对象受力状态更稳定；③双臂协调抓捕刚度更高，增加抓捕的成功率；④相互配合，提高操作灵活性。综合考虑系统复杂度与可靠性，空间双臂系统能够为空间机器人提供更大的操作柔性，从而更适合在轨服务任务。综上所述，采用双臂对目标星进行转位是一类典型的双臂协调操作任务。

然而，双机械臂控制会涉及到一些单机械臂控制不会遇到的新问题，如运动协调与负载分配等。尤其是当机械臂完成对目标的抓捕并形成闭链后，各臂之间存在运动约束，此时双臂之间强耦合，操作物的期望运动轨迹完全决定了各机械臂在操作空间的运动轨迹，双臂协调运动问题更为突出。双臂机器人操作物体时，不仅需要机械臂位置之间的协调控制，同时为了防止机械臂与物体的接触力过大而损坏物体，还需要对物体与机械臂之间的接触力进行协调控制。双机械臂异构、刚度不同、测量/执行误差、抓捕位置随机偏差等因素，可能引起双臂实际轨迹偏离期望轨迹，使得实际轨迹可能不满足闭链约束，从而导致双臂与目标间接触力过大甚至协调转位任务失败。显然，这增加了系统分析和控制的复杂度，也对双机械臂之间的协调规划与控制提出了更高要求。

从双臂机器人技术的发展过程来看，可以将双臂机器人协调控制方法分为以下几类[2]：纯位置控制、主从控制、力/位混合控制和阻抗控制。

纯位置控制仅通过控制两条臂之间的位置关系，从而实现对物体的操作。这种方法对两臂的运动学参数要求较高，并需要对机械臂进行高精度标定，适用于系统的位置柔性较大的情况[3]。

主从控制将一条臂视为主臂，另一条视为从臂，主臂按照预定轨迹运动，从臂在操作物体上施加一定的力跟随物体运动。在一般的主从控制中，主臂仅采用纯位置控制，而从臂仅采用纯力控制[4]。这种控制方式较为简单，在从臂能够快速响应的情况下，可以实现较为满意的控制效果。

力/位混合控制方法克服了主从控制在处理双臂协调性问题上的不足，两条机械臂不分主次。双臂在自由空间采用位置控制，在约束空间采用力控制，如文献[5-9]。但是，该控制方式在自由空间向约束空间过渡过程中需要进行位置/力控制的切换，尤其在操作状态发生变化的情况时，双臂系统的力控制和位置控制存在阶跃跳变的情况，对于稳定操作物体非常不利。

阻抗控制由Hogan[10]提出，该方法不是控制机器人与环境的接触力，而是根据机器人端部的位姿和作用力信息，建立两者之间的关系，通过调整位姿误差或者刚度系数来达到调节机械臂作用力的目的[11-12]。因此，为达到较好的控制效果，阻抗控制方法需要精确掌握接触环境信息。Wimbock等[13]在两个机械臂之间建立耦合弹簧模型用于调节物体的内力，解决了双臂机器人操作物体时内力过大的问题，但是没有考虑外界干扰力的影响。Bonitz等[14]提出了基于力的双臂阻抗控制方法，实现控制物体的运动和控制机械臂与物体之间的内力。Lee等[15]提出了一种相对式阻抗控制方法用来处理双臂非对称操作任务。Caccavale等[16]提出了一种可以同时实现物体阻抗和机械臂笛卡尔阻抗控制的双臂协调控制方法。Schneider等[11]针对双臂操作物体，提出了物体阻抗控制方法，用来控制物体操作的内力。Heck等[17]提出了基于内力和外力的双臂阻抗控制方法，在物体和环境之间建立了物体阻抗关系，在机械臂与物体之间建立了笛卡尔阻抗关系，但并未明确两个阻抗关系是如何协调实现的。Ren等[18]提出了一种仿人物体阻抗控制方法，也是采用内外阻抗环的形式。虽然上述研究考虑了双臂对物体的内力和外力控制，但是大部分都采用定阻抗的控制策略，并没有考虑同时存在外部干扰和内力约束的情况。

综上可知，对于双臂协调转位任务，相对于复杂的内力优化策略[19]，主从控制方法相对简单，能有效解决双臂协调转位过程中同时存在外部干扰和内力约束的问题，因此更加适合在轨应用。然而，传统的主从控制方法将两条臂简单划定为主臂与从臂，主臂的所有关节进行主动运动，从臂的所有关节进行跟随运动。在两条臂的尺寸、自由度、动力学参数存在较大差异的情况下，主臂/从臂的简单划定策略可能导致双臂协调转位任务无法顺利完成。为此，本文提出了一种基于主动关节/从动关节划分的空间大质量目标转位操作双臂协调控制方法。该方法能够基于任务需要，灵活划分主动关节与从动关节，从而达到更好的协调控制效果。首先，根据双臂协调转位任务特点，建立双臂间的主从约束关系，进行双臂协调转位运动规划。然后，将双机械臂的所有关节分别划分为主动关节和从动关节，并对主动关节设计关节位置控制器，对从动关节设计零力控制器。最后，对空间质量目标转位操作双臂协调控制方法进行了数学仿真验证。

1 空间质量目标转位操作双臂协调控制

需要指出的是，双臂协调转位任务中的“协调”体现在，在转位过程中，两部机械臂末端与目标星之间的接触力均不能过大，以保证转位操作的安全性。本文首先针对双臂转位任务进行机械臂轨迹规划，然后设计空间大质量目标转位操作协调控制方法，通过划分主动关节与从动关节，并分别为这两类关节设计控制器，从而实现了双臂协调转位控制。

为了使双臂在执行协调转位任务时更加灵活，本文中假定两部机械臂均具有七个自由度。

1.1 转位过程的轨迹规划

转位是指如何通过规划机械臂各关节的运动轨迹，使目标星从某一初始位姿运动到期望位姿(通常是更适合机械臂操作的位姿)，从而可以更好地对失效目标进行维修、维护、升级等操作。

本节双臂协调转位控制策略中，以目标星的期望位置和期望姿态为约束，设计一条目标星从初始位姿运动到期望位姿的期望轨迹，进而求解两部机械臂各关节的运动轨迹，最后通过轨迹跟踪控制完成目标星的转位操作，如图1所示。

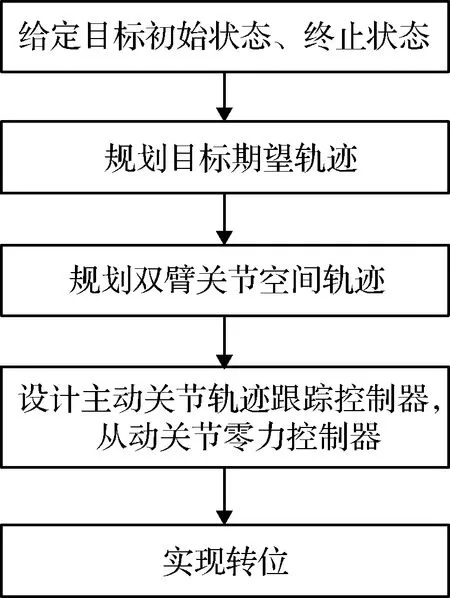
图1 双臂协调转位控制策略Fig.1 Flow chart of the dual-arm coordinated transposition control algorithm

1.1.1目标位姿期望轨迹规划

当需要机械臂的末端执行器按事先给定的轨迹相对星体运动时，可采用离线轨迹规划的方法。一般可先进行位姿路径规划，再给定按轨迹运行的时间历程，完成轨迹规划。

对位置，可规划机械臂末端在基座参考系中的直线路径

(1)

令bRt,i,bRt,f分别为机械臂末端在起点、终点处相对于基座参考系的姿态，则初、末点的相对姿态为

t,iRt,f=[bRt,i]TbRt,f

(2)

于是，可由t,iRt,f得到欧拉轴t,iat,f和转角t,iθt,f，其中t,iθt,f>0。进而，可规划相对基座参考系的单轴转动姿态路径

(3)

式中：so∈[0,sof],sof=t,iθt,f。机械臂末端相对于基座参考系随时间变化的姿态t,iRt可由轴t,iat和so计算得到。

假设给定上述st和so随时间t的变化规律st(t)和so(t)，则根据式(1)和式(3)可确定位姿轨迹，即

(4)

(5)

为使机械臂平滑地由静止启动、运动、停止，st(t)和so(t)可由五次多项式进行规划。不失一般性，考虑如下五次多项式

(6)

假设运动初始时刻为t0，期望轨迹的初始值为x0，停止时刻为tf，终值为xf，并要求在开始和停止时有x的一、二阶变化率为零，即

(7)

由式(7)，有

(8)

由式(8)求解a0～a5即可得到满足条件的轨迹。

1.1.2关节期望轨迹规划

(9)

(10)

则系统的关节期望运动轨迹为：

(11)

关节角加速度、关节角可分别通过数值求导、积分得到。

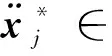
(12)

此时，可将每部机械臂各关节的期望运动轨迹规划为：

(13)

式中：En为单位矩阵；KD为正定对称矩阵，右端第二项利用冗余自由度使得在机械臂完成任务的过程中角速度尽量小。关节角速度和关节角轨迹可通过积分得到。

1.2 主动/从动关节控制器设计

转位过程的被控对象为机器人-目标闭链组合体，转位控制需考虑目标质量特性和闭链约束的影响。本节以降阶的闭链动力学方程为基础进行控制器设计。

1.1节中规划双臂各关节的轨迹时，使用了机械臂末端完成捕获时相对目标的位姿。由于存在抓捕误差，实际中无法精确获知上述几何参数，使得规划的轨迹可能不满足实际的闭链约束。此时，若各关节跟踪各自的轨迹，可能造成机械臂与目标接触力饱和，从而对目标造成破坏。

实际上，由于存在约束，在平台-机械臂-目标组成的闭链中，主动关节的个数少于两部机械臂的关节数之和。若仅使主动关节跟踪给定轨迹，而使从动关节在机械臂末端与目标星之间作用力的牵引下自由运动，则可以回避规划轨迹与闭链约束间的矛盾，从而防止接触力过大。这里，从动关节的控制器为基于机械臂腕部力传感器测量数据的零力控制器，该类关节的轨迹不受控。

从几何约束上看，形成闭链后，各关节变量间将不再是相互独立的，而是受到闭链的约束。选出一组与闭链自由度数相同的关节作为主动关节，其余关节的变量可由主动关节变量和闭链约束自动确定，定义为从动关节。进行控制时，基于主动关节相关测量，对主动关节进行位置控制；从动关节则在机械臂末端受力牵引下运动。

对本文中考虑的双臂系统，取平台的平动和转动、第1部机械臂的7个自由度和第2部机械臂的第1个关节自由度为系统的主动自由度；另外，平台不受控，目标除机械臂的作用外不受力。因此，系统的动力学方程可写为

(14)

式中：HIb为平台的惯量矩阵；HIbm为平台与机械臂(仅考虑主动关节运动)之间的耦合惯量矩阵；HIm为机械臂(仅考虑主动关节运动)的惯量矩阵；cIb为平台的科氏力与离心力；cIm为机械臂(仅考虑主动关节运动)的科氏力与离心力；Gbm为机械臂末端与平台之间的雅克比矩阵；Gm为机械臂末端与机械臂基座之间的雅克比矩阵。

(15)

式中：

(16)

(17)

(18)

(19)

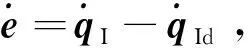
(20)

式中：KD,KP为可设计的正定对称阵。

从动关节采用基于位置控制的零力控制方法，其核心是将外力的大小及方向转换为对应的位置指令。外力信息的获取主要有两种方式，一种是通过腕部力/力矩传感器或关节力矩传感器实现对外力的检测；另一种是采用估计的方法，将反馈力矩与经动力学模型计算的力矩做差，该差值即为所估计外力的大小。本文采用基于传感器的实现方案，相对于采用估计的方案，其优点是：①能够比较精确地检测外力的大小，系统灵敏度较高；②由于有传感器作为外部测量反馈，系统稳定性有更好保证。

2 仿真校验

操控星与目标星的本体尺寸均为2360 mm(X)×2100 mm(Y)×4300 mm(Z)。

操控星与目标星的本体系定义为：原点均在各自质心处；Z轴——垂直于卫星对接环所在平面，从原点指向对地板；Y轴——沿卫星帆板方向，从原点指向卫星南侧舱板；X轴与Y轴、Z轴构成右手系。

1)操控星的质量特性见下表。

表1 操控星质量特性Table 1 Inertia parameters of the chaser satellite

目标星质量惯量参数见下表。

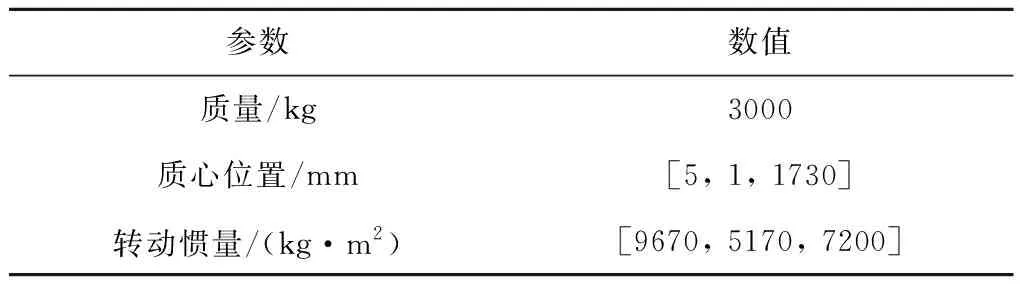
表2 目标星质量特性Table 2 Inertia parameters of the target satellite

2) 操控星上安装有两部机械臂。两部机械臂的运动学结构完全一致，采用修正的DH(MDH)参数进行描述，如表3所示。其中，臂1的质量为100 kg，其根部安装位置为[-1180, 850, 4190]Tmm；臂2的质量为90 kg，其根部安装位置为[-1180, -750,4190]Tmm。惯量计算中视各杆为圆柱形均质实心杆，直径均为110 mm。各杆的质心在圆柱的几何中心处。两臂的质量特性参数如表4和表5所示。

表3 两部机械臂的MDH参数Table 3 MDH parameters of both manipulators

表4 臂1质量特性Table 4 Inertia parameters of Manipulator #1

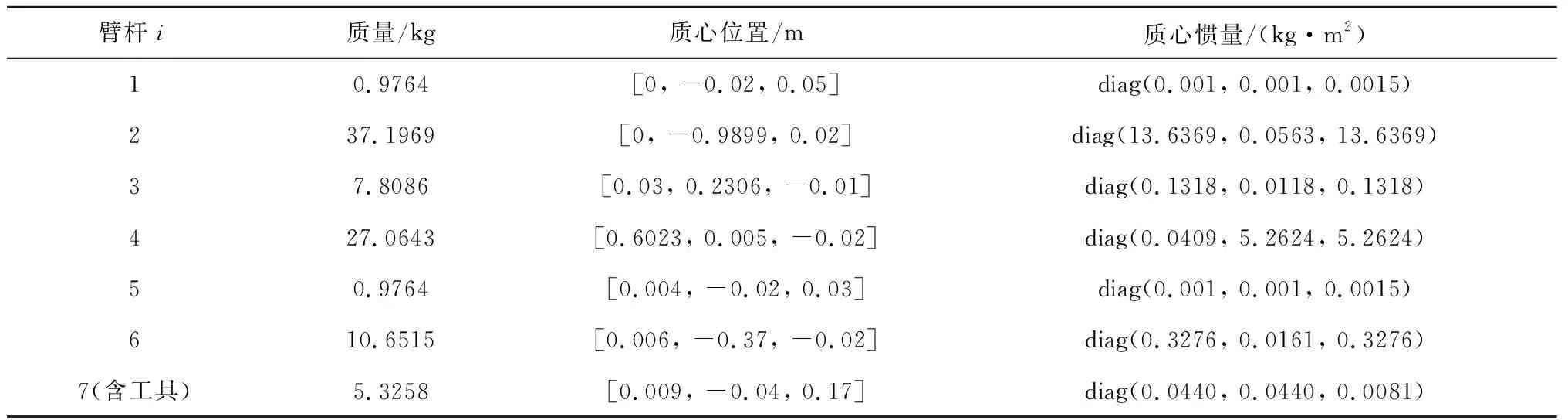
表5 臂2质量特性Table 5 Inertia parameters of Manipulator #2

3)目标相对平台的初始位置为[0.3, 0.5, 7.3]Tm，期望位置为[-1, 0, 7.3]Tm。目标相对于平台的初始姿态角(3-2-1转序)为[90°, 14°, 4°]，期望姿态角为[90°, 0°, -15°]。

4)在转位开始前，目标和平台相对于惯性系处于静止状态，即由目标和平台(含两部机械臂)组成的系统的初始动量为零。

目标星体坐标系相对操控星平台体坐标系的位姿如图2所示，可见目标转位完成。目标星和操控星平台相对于惯性系的位姿、速度、角速度分别如图3、图4所示。由图3、图4可知，在完成转位后，目标、平台也恢复到静止状态，满足动量守恒定律。

图2 目标星体坐标系相对操控星平台体坐标系的位姿Fig.2 The relative pose of the body frame of the target satellite w.r.t that of the chaser satellite

图3 目标星相对惯性系的位姿、速度、角速度Fig.3 The pose, speed and angular velocity of the target satellite w.r.t the inertial frame

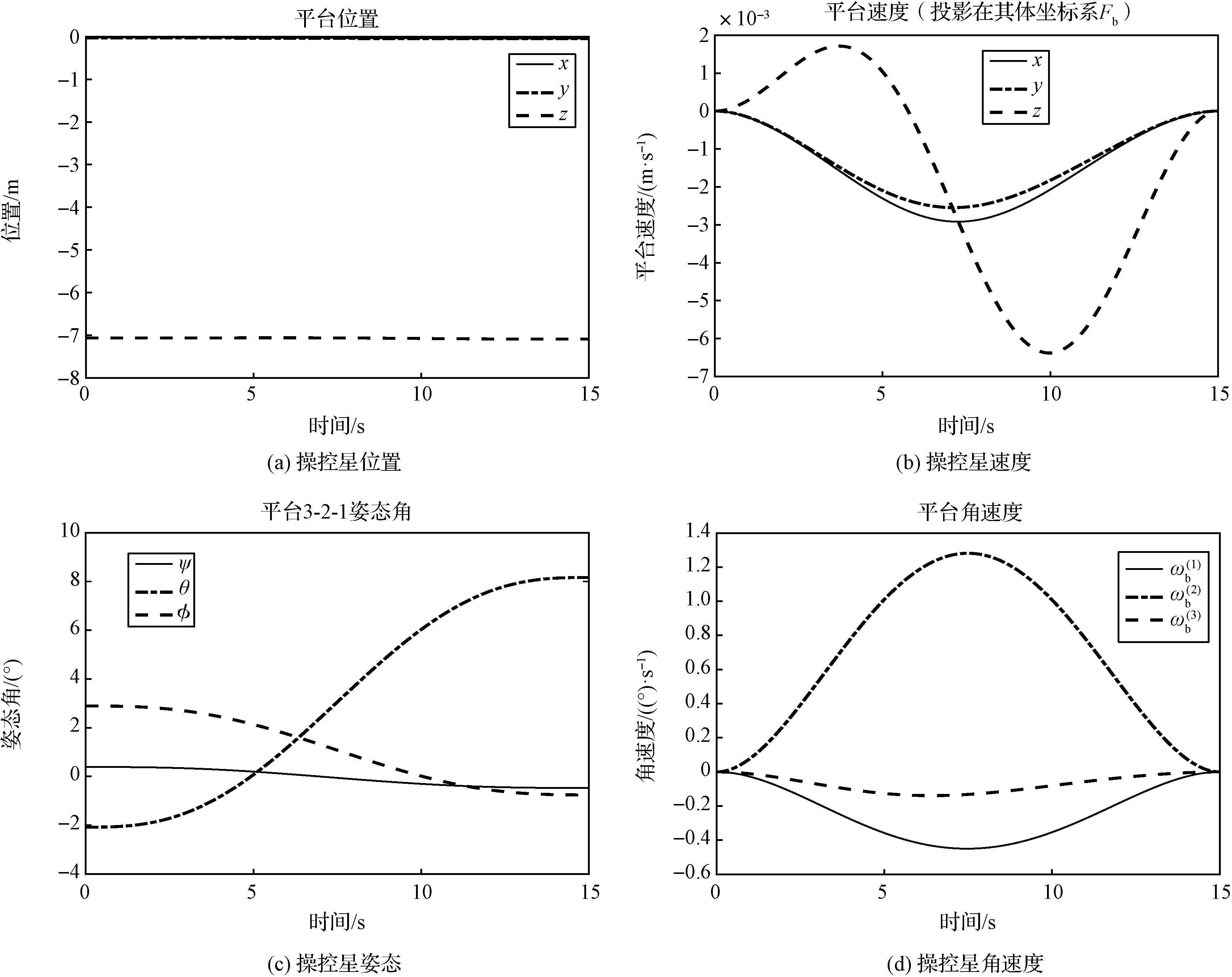
图4 操控星平台相对惯性系的位姿、速度、角速度Fig.4 The pose, speed and angular velocity of the chaser satellite w.r.t the inertial frame

两部机械臂的相关变量如图5、图6所示。从仿真曲线可以看出，两部机械臂14个关节均趋于期望位置。由图5、图6可知，两部机械臂的末端受力均小于10 N，均处于安全范围内。在转位过程中，两部机械臂与目标间的接触力较为平滑，不会出现幅值过大或者突变的情况。

图6 机械臂2相关变量Fig.6 The related variables of Manipulator #2

通过以上仿真可以发现，采用本文提出的空间质量目标转位操作双臂协调控制方法，不仅能够成功完成转位操作，而且能够将两部机械臂末端与目标之间的接触力控制在较小范围内。

3 结 论

本文对空间大质量目标转位操作协调控制方法进行了研究。针对空间大质量目标双臂协调转位任务中面临的双机械臂异构、刚度不同、负载较大、测量/执行误差、抓捕位置随机偏差等问题，首先进行了转位过程的双臂协调轨迹规划，然后将双臂所有关节划分为主动/从动关节。主动关节采用位置控制器；从动关节的控制器为基于机械臂腕部力传感器测量设计的零力控制器，该类关节的轨迹并不受控，仅在机械臂末端与目标之间接触力的带动下运动。这样就能保证双臂末端始终满足闭链约束，且双臂末端与目标间内力处于可控范围内。最后，通过数学仿真表明了本文中所提方法的有效性。