刀具非对称刃口瞬时铣削力建模与实验研究
2022-01-29赵雪峰杨勇秦浩李辉
赵雪峰 杨勇 秦浩 李辉
(贵州大学 机械工程学院,贵州 贵阳 550025)
随着制造业向高精密和超精密方向发展,对刀具也提出了更高的要求。刀具钝化通过改变切削刃的微观形貌提高刀具的寿命、切削过程的稳定性和已加工表面的质量[1- 4]。刀具钝化后刃口并非规则对称的圆弧,刀具钝化刃口对切削力的影响非常大。切削力作为切削加工中的重要参数,对刀具磨损、加工质量有重要的影响[5],瞬时铣削力模型是铣削加工动力学特性以及加工参数最优选择的关键[6- 7]。因此,研究刀具钝化非对称刃口的铣削力对揭示刀具钝化的作用机制和刀具的切削机理具有重要意义。
铣削力模型的建立主要分为解析法、经验法和机械建模法。其中机械建模法兼具前两种方法的优点,是切削力预测中最精准的建模方法,因此应用广泛[8]。机械建模法的精准程度取决于切削力系数以及瞬时切削厚度的确定。Altintas等[9]假设切削力与进给速度线性相关,并以进给速度为变量设计铣削实验,通过实验获取不同进给速度下的平均切削力,采用线性拟合的方法获得相应的切削力系数;Grossi等[10]在研究主轴转速对切削力的影响规律时,进行了一系列铣削实验,对铣削力进行高频滤波处理,并采用瞬时切削力提取切削力系数;Budak等[11]提出了不需要对每个铣刀几何形状进行实验校准的切削力系数模型,可用于复杂刀具,极大地简化了复杂刀具的切削力分析。由于刀具刃口钝圆的存在,在切削过程中存在负前角切削现象,对此研究者提出了有效前角的概念,从而可在考虑刃口尺寸的切削力分析中使用现有的切削力系数模型。Wen等[12]建立了考虑后刀面磨损的立铣刀动态切削力模型,采用未磨损与磨损后的刀具以相同的切削参数进行切削实验,确定由于后刀面磨损而产生的额外切削力,提取后刀面切削力系数。万敏等[13]对单向CFRP螺旋铣削力建模时通过槽铣的方法标定侧刃切削力系数,通过直线半齿插铣的方法标定底刃切削力系数,建立底刃和侧刃切削力系数与切削几何关系的数据库,并利用该数据库对BP神经网络进行训练,建立切削力系数的神经网络计算模型。
Denkena等[14]通过一系列研究证明,刀具刃口尺寸的存在是产生犁耕现象的主要原因。犁耕过程对于加工表面质量具有重要影响,因此一直都是研究热点。根据犁耕作用会引起工件材料挤压从而产生弹塑性变形的特点,在对犁耕力进行分析时多应用滑移线场理论。而当接触边界为非直线时,滑移线场异常复杂。针对刀具刃口形貌的复杂性和非直线接触边界的特点,研究者均将接触边界转化或简化为直线接触。Waldorf等[15]在计算刃口钝圆半径产生的犁耕力时,以刃口前端形成的金属死区边界直线作为滑移线场边界作用线,建立了犁耕力模型;Jun等[16]在计算刀具刃口产生的犁耕力时,将产生犁耕作用的弧形刀面投影为直线作用面,并建立相应模型。
以上研究都是针对刀具刃口为标准圆弧的情况,而实际生产中使用的刀具,特别是经过钝化处理的刀具刃口大多为非对称的圆弧。因此,本研究针对刀具钝化非对称刃口,结合微元铣削力模型,将刃口尺寸效应反映在切削力系数中,建立了刀具非对称刃口瞬时铣削力模型。
1 刀具非对称刃口瞬时铣削力模型
1.1 刀具钝化非对称刃口表征
刀具钝化非对称刃口表征如图1所示,常用形状因子k(k=Sγ/Sα)来表示刀具钝化非对称刃口。假设刀具非对称刃口前、后刀面相切于刀尖角的角平分线上,切点为C,所包含的前、后刀面分别为标准圆弧的一部分,圆弧半径分别为r1和r2。由几何关系,已知前、后刀面钝化值Sγ、Sα,即可
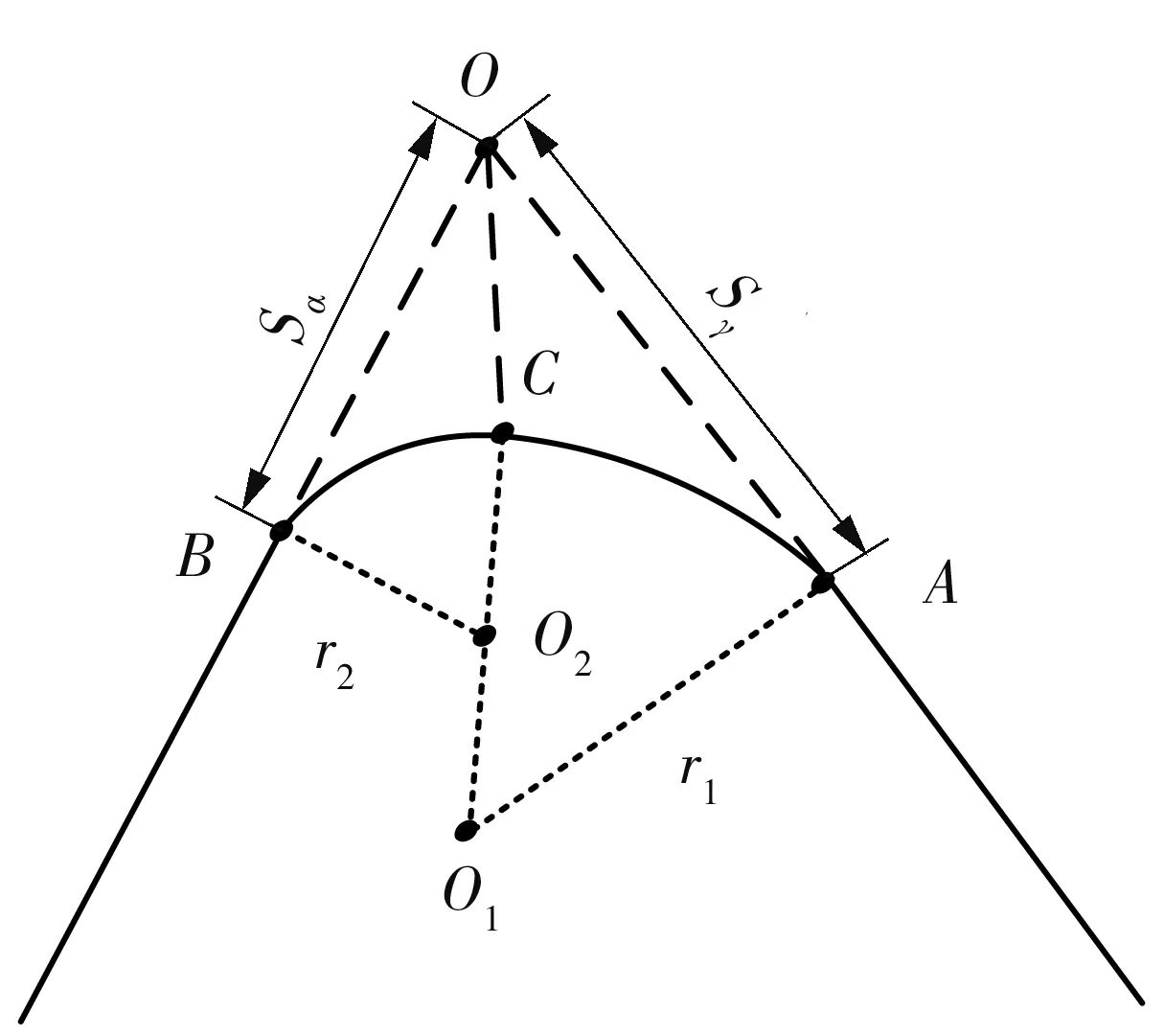
图1 刀具钝化非对称刃口示意图Fig.1 Schematic diagram of asymmetric edge of cutter passivation
求得相应的r1和r2,为后面根据瞬时切削厚度对切削阶段的划分提供依据。
1.2 等效犁耕作用刀面
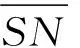
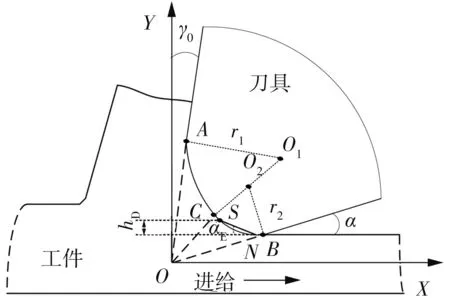
图2 等效犁耕作用刀面示意图Fig.2 Schematic diagram of equivalent ploughing action cutter surface
1.3 刀具非对称刃口瞬时铣削力模型
为模拟铣削过程中的切削力,将刀具沿轴向离散为一定数量的微元切削刃,对应于工件的切削单元。对于整个刀齿受到的切削力,由该齿参与切削的微元切削刃受到的切削力在切削区间内进行数值积分获得。如图3所示,建立与工件联接的直角坐标系X-Y-Z以及与刀具联接的圆柱坐标系r-θ-h,其中dFt、dFr、dFa分别为刀具受到的切向力、径向力、轴向力,ap、ae分别为切削深度与宽度,n为刀具转速。则第i个刀齿的任意瞬时齿位置角θi处(位置角θ可由时间t求得)的微元切向、径向、轴向力分别为dFt,i(t)、dFr,i(t)、dFa,i(t),其中i=1,2,3,…,N,N为铣刀齿数。在X方向的切向力dFx,i(t)与Y方向的法向力dFy,i(t)可通过位置角θi经过角度变换获得,切削力Fx、Fy、Fz为所有切削微元在X、Y、Z方向上切削力的总和。
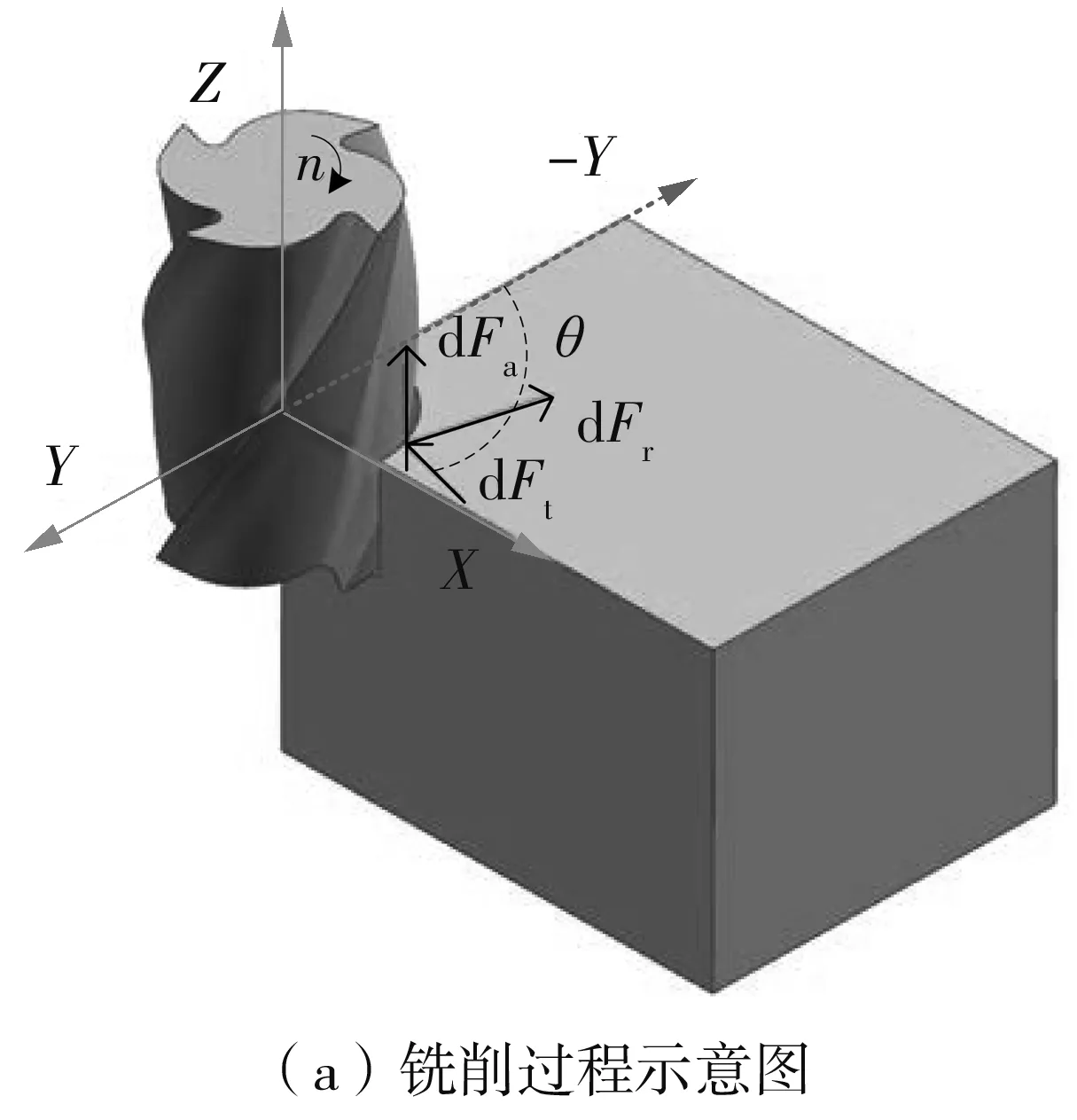
图3 整齿铣削与微元铣削示意图Fig.3 Schematic diagram of whole tooth milling and micro element milling
由Altintas等[17]提出的动态铣削力模型可得微元切削力dFt,i(t)、dFr,i(t)、dFa,i(t)分别为
(1)
式中:Kt,剪切、Kr,剪切、Ka,剪切分别为剪切作用在切向、径向、轴向的切削力系数;Kt,犁耕、Kr,犁耕、Ka,犁耕分别为犁耕作用在切向、径向、轴向的切削力系数;dz为微元切削刃轴向厚度;h(θi)为微元切削刃的瞬时切削厚度;S(h)为微元切削刃产生犁耕效应的刀面作用长度。
刀刃i在轴向高度Z处切削微元的展开如图4所示,其中hD为最小切削厚度,fz为每齿进给量,h为实际切削厚度。由图4(b)中所示的微元切削力与直角坐标系之间的关系,可将dFt,i(t)、dFr,i(t)、dFa,i(t)通过微元切削刃位置角θi,经过角度变换,获得在工件坐标系X、Y、Z方向上的微元切削力dFx,i(t)、dFy,i(t)、dFz,i(t):
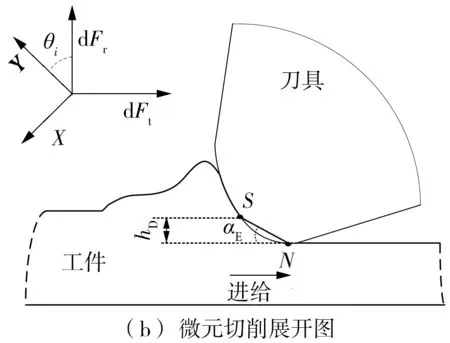
图4 刀刃i在轴向高度Z处切削微元展开示意图Fig.4 Expanded schematic diagram of cutting micro element of blade i at axial height Z
(2)
对于整个刀齿i的切削力可由该刃上所有参与切削的微元切削力沿Z轴积分得到:
(3)
式中,积分上、下限zj、zi由切削微元所处的不同切削阶段确定。
1.4 瞬时切削厚度
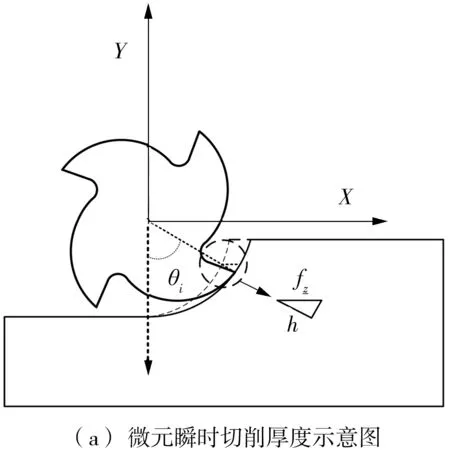
微元切削刃的瞬时切削厚h(θi)与其位置角θi有关。由图3可知,第i条切削刃上任意轴向高度Z处的微元切削刃在t时刻的位置角为

(4)
式中,θi,0为第i条切削刃上Z=0处的微元切削刃转角,φ(z)为滞后角。
其中

(5)
式中,n为刀具转速,N为刀具齿数。
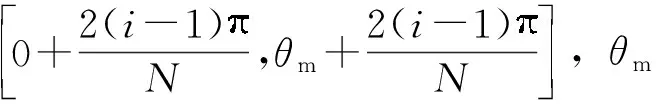
(6)
由于刀具螺旋角的存在,使得在切削中每一处微元切削刃相对于其最底边切削刃都存在不同程度的滞后现象,该现象可通过滞后角φ(z)进行描述。根据几何关系可知:
(7)
式中,z为微元切削刃轴向高度,β为刀具螺旋角。
由图4可知:
(8)
(9)
1.5 剪切作用系数
剪切作用系数Kt,剪切、Kr,剪切、Ka,剪切与工件、刀具材料以及铣削参数有关,计算公式如式(10)所示。Budak等[11]对比分析了机械力学与统一力学方法,提出以下模型,该模型不需要对每个铣刀的几何形状进行实验校准便可用于机械力的预测,并可应用于复杂的刀具。
(10)
式中,γ0为刀具前角,s为剪切屈服应力,βn为平均摩擦角,ηc为切屑流动角,φc为剪切角。
对于式(10)中刀具前角γ0的选择为:刃口处采用有效前角γi作为刀具前角[18],其余部分为刀具实际前角。
(11)
式中,ri为刃口钝圆半径。
对于刀具钝化非对称刃口,分离点S的位置如图5所示。
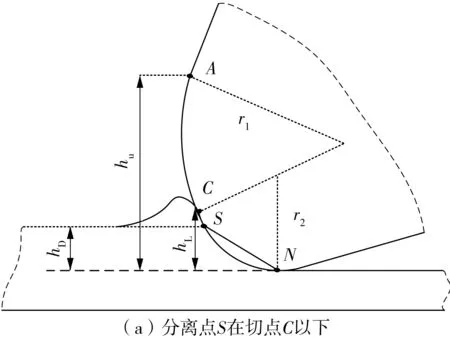
图5 分离点S与切点C的相对位置示意图Fig.5 Schematic diagram of relative position of separation point S and tangent point C
由图5可知,hL为刃口处前、后刀面切点C到已加工表面的距离,hU为刃口处前刀面与刀具初始前刀面的切点A到已加工表面的距离。当切屑在不同刃口圆弧面上产生时,有效前角如下。
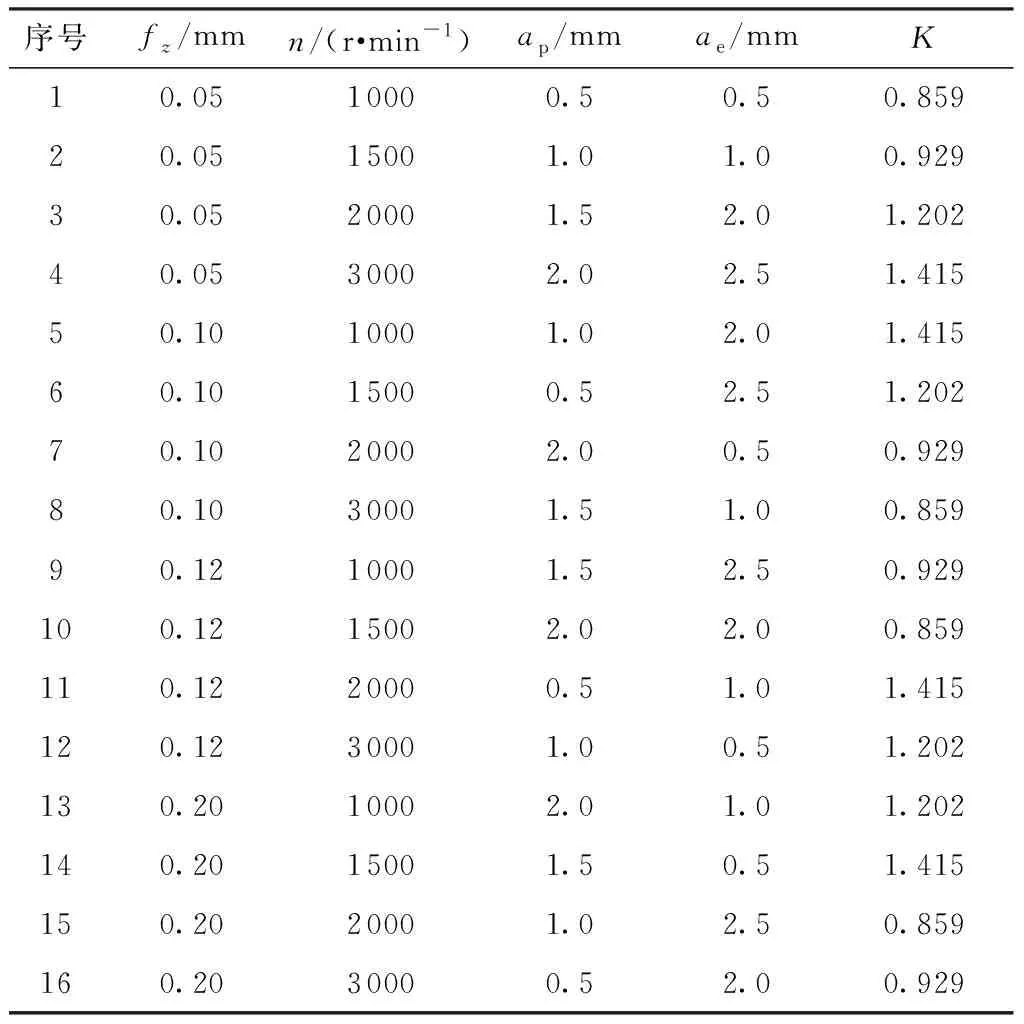
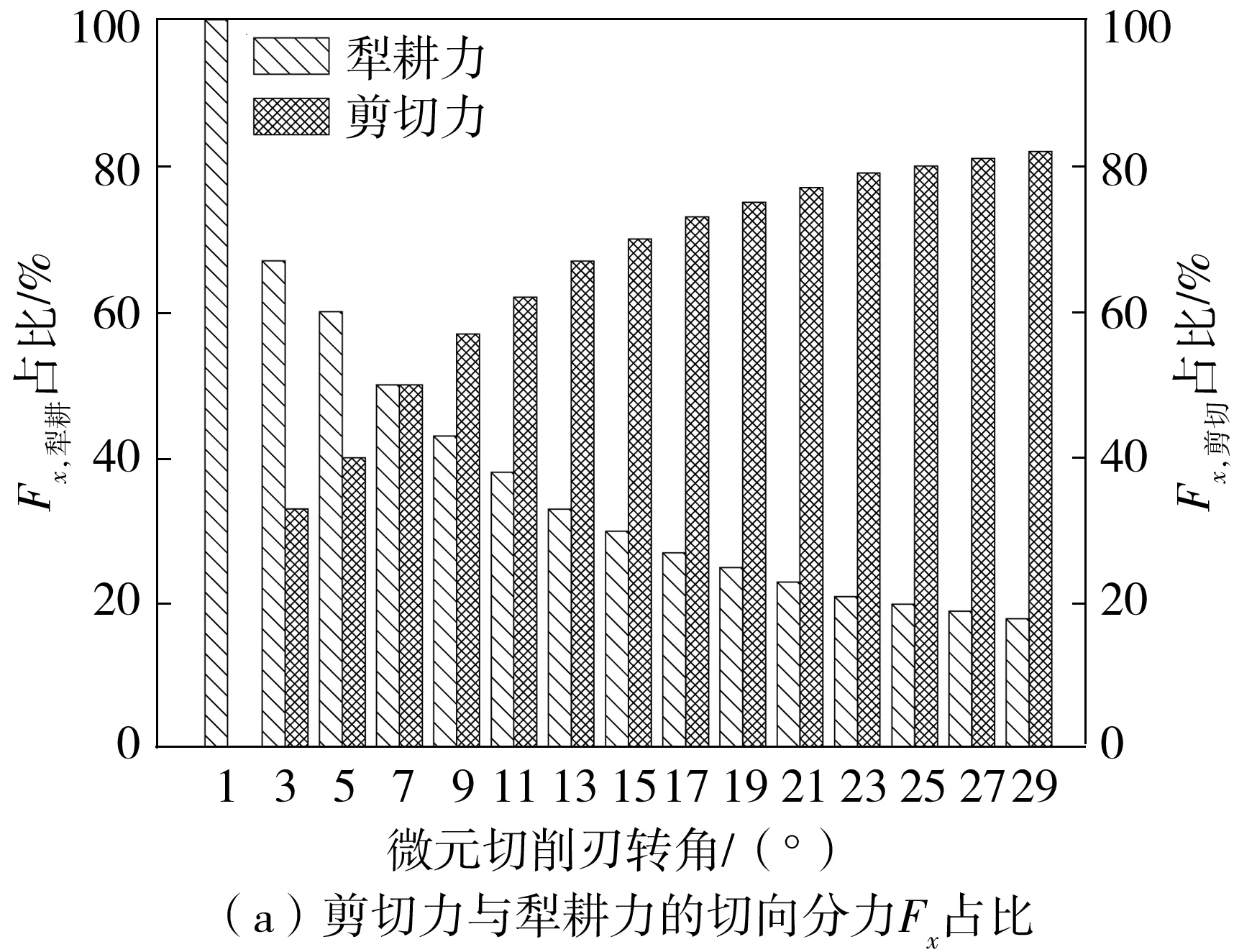
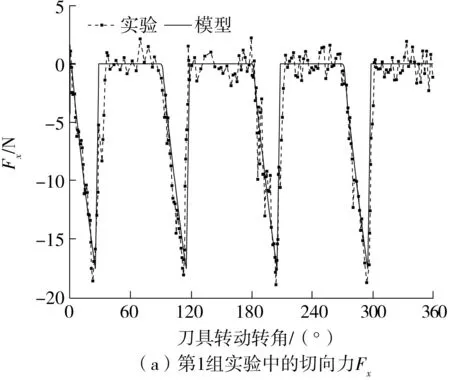
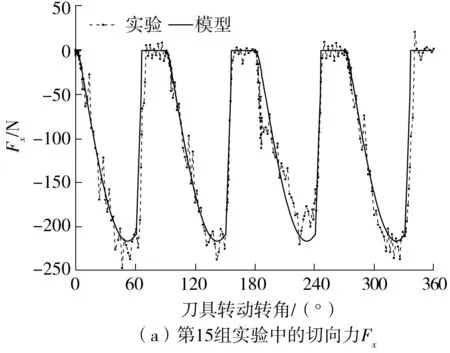
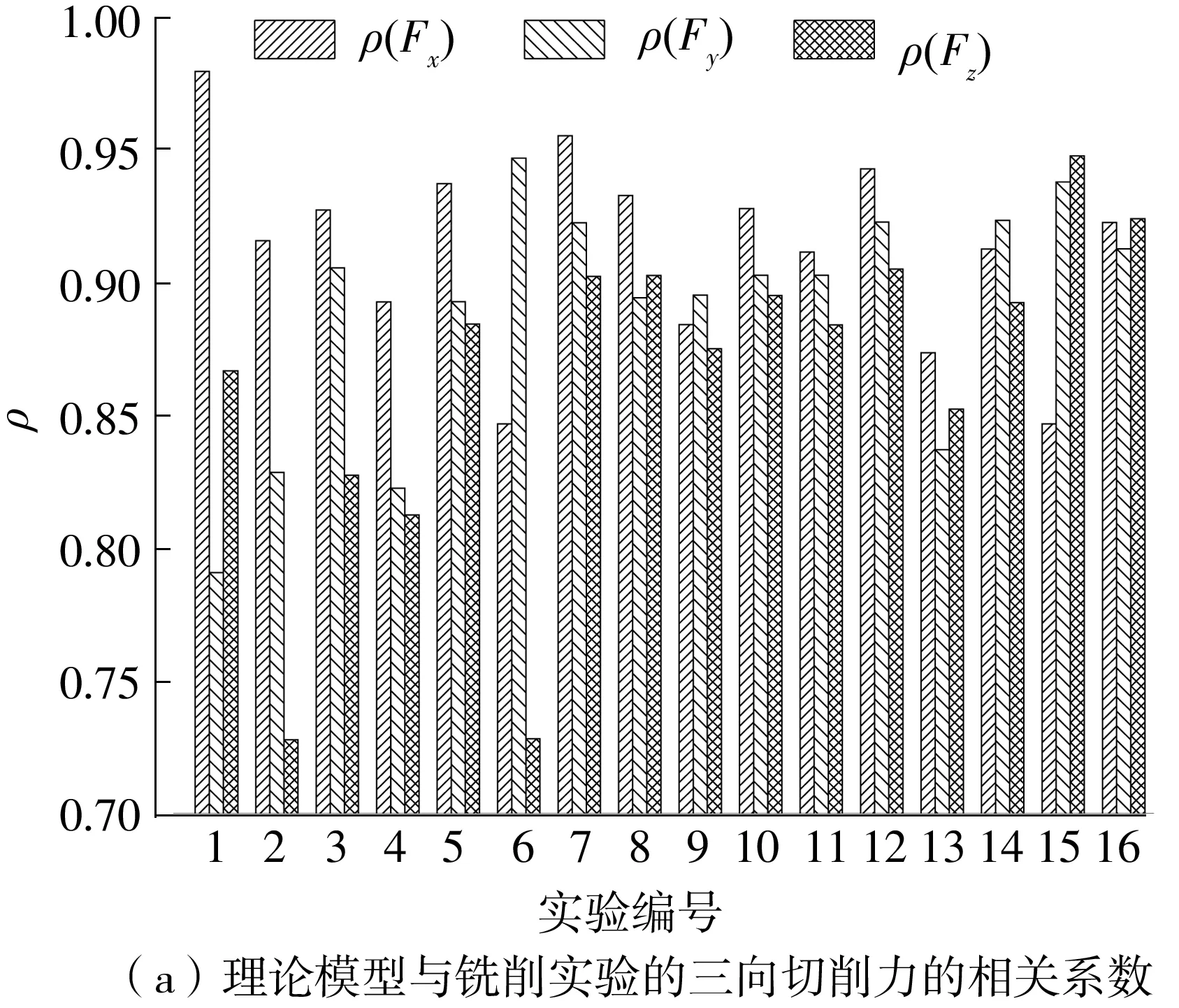
(1)当分离点S在前、后刀面切点C以下时(如图5(a)所示),即hD (12) (2)当分离点S在前后刀面切点C以上时(如图5(b)所示),即hD>hL,式(11)中半径ri的取值为 ri=r1,hL (13) (14) 采用硬质合金刀具铣削AISI 1045钢,材料的Johnson-Cook本构参数如表1所示。 表1 AISI 1045 钢的Johnson-Cook本构参数[19]Table 1 Johnson cook constitutive parameters of AISI 1045 steel 平均摩擦角βn与刀屑平均摩擦系数μ的关系为[20] (15) 式中:f0取常数0.704;p取常数-0.248;V为切削速度,m/min。 切屑流动角ηc与切削角度参数之间关系为[21] (16) 根据Merchant[22]的剪切理论,剪切角φn为 (17) 基于刀具非对称刃口的等效犁耕作用刀面的特点,以及滑移线场基本理论,建立刀具非对称刃口犁耕力滑移线场模型,如图6所示。线场中各个区域的定义及划分原则可参考文献[23- 24]。 滑移线为塑性平面应变状态下变形体内各质点最大切应力的迹线。根据平面塑性应变的特点,Hencky提出各质点应力分量可由平均应力σm和最大切应力K表示,并给出关系式,即Hencky应力方程: (18) 式中,ξ、v为积分常数,ω为α滑移线在任意点P的切线正方向与Ox轴的夹角。 根据式(18)对图6所示的滑移线场进行求解: σm,H-2KωH=σm,N-2KωN (19) 式中,σm,H为H点平均应力,由于H点在自由边界HI上,故σm,H=-K,同时可知角∠GHI为45°。 根据几何关系可知 (20) 则N点平均应力为 σm,N=-K-2K(ωH-ωN) (21) 由应力状态和应力莫尔圆可知,N点正应力、切应力分别为 (22) 根据滑移线场的性质可知,N点处的正应力σ和切应力与整个SN面上相同,于是由图4(b)所示的几何关系可得微元切削刃SN面上所受犁耕力在切向、径向分力分别为 (23) 由式(23)可知犁耕作用系数Kt,犁耕、Kr,犁耕分别为 (24) 由于滑移线场理论主要适用于平面应变状态下,而轴向力与切向、径向力处于三维空间中,故将犁耕作用产生的轴向力认为是由切向力通过刀具螺旋角作用产生的,即: Ka,犁耕=Kt,犁耕tanβ (25) 由于铣刀螺旋角的存在,每个刀刃在切削过程中为逐渐切入、切出,因此会经历3个不同的切削过程,即切入过程、持续切削过程、切出过程。对于每个微元切削刃,根据切削中瞬时切削厚度的不同,也会存在3种不同的切削阶段,如图7所示,即犁耕阶段、犁耕与刃口前刀面剪切同时作用阶段、犁耕-刃口前刀面剪切-刀具初始前刀面剪切同时作用阶段。由于随着瞬时切削厚度的不同,式(1)中矩阵元素也随之变化,因此在整个切削刃的不同切削过程中,微元切削刃所处的不同切削阶段将通过对积分限的再划分体现在积分区间中,极大地提高了计算效率。 (1)切入过程 从铣刀某一刀刃最底端微元切削刃开始接触工件到轴向高度为ap处的微元切削刃开始接触工件的这一过程为切入过程。这一过程刀具的转角φi,0可由轴向切深ap与刀具半径R求得: (26) 因此,由式(26)可得进入切削过程中参与切削的微元切削刃轴向区间为 (27) (2)持续切削过程 从铣刀某一刀刃轴向高度为ap处的微元切削刃开始接触工件到最底端切削刃开始脱离工件接触的这一过程为持续切削过程。由于这一过程切削刃所有微元均参与切削,故式(3)中积分限为 (28) (3)切出过程 铣刀某一刀刃最底端微元切削刃开始脱离工件接触到轴向高度为ap处的微元切削刃开始脱离工件接触的这一过程为退出切削过程。这一过程中式(3)的积分限为 (29) 在刀具钝化非对称刃口切削过程中,形状因子(K)、每齿进给量(fz)、主轴转速(n)、轴向切深(ap)和径向切深(ae)都对切削力具有重要的影响。为验证所提出的铣削力模型的正确性,设计正交实验方案,如表2所示。在数控铣床VCL850上进行铣削实验(如图8所示)。刀具为硬质合金刀具ZX04,直径10 mm,前角14°,后角15°,螺旋角30°。工件材料为45号钢,采用三通道压电式测力仪Kistler-9257B型进行铣削力信号采集,采样频率为5 kHz。 表2 铣削正交实验方案Table 2 Milling orthogonal experiment scheme 图8 铣削实验Fig.8 Milling experiment 为研究由非对称刃口作用产生的犁耕力在整个切削过程中的重要性,以第1组实验方案为例,对微元切削刃整个切削过程进行分析,犁耕力与剪切力随着切削厚度(切削厚度与切削刃转角成正比)的不同其各自在总切削力中的占比如图9所示。 图9 剪切力与犁耕力占比Fig.9 Proportion of shear force and ploughing force 由9图可知,在整个切削过程,随着切削厚度的增大,犁耕力所占比重逐渐减小,但其切向分力Fx,犁耕、径向力分Fy,犁耕的占比均在20%以上(这里的Fx、Fy分别为铣削力过程中的切向力与径向力,而不论是剪切力还是犁耕力都最终分解为切向力与径向力。因此,其分解在切向力方向的称为切向分力,分解在径向力方向的称为径向分力)。并且,在将要切出的过程中,犁耕力的径向分力Fy,犁耕所占比重有上升的趋势。因此,刀具非对称刃口作用产生的犁耕力在整个切削过程中至关重要。 第1组和第15组的铣削力理论模型结果与实验结果对比分析如图10、图11所示。 由图可知,各铣削分力的变化趋势,特别是曲线拐点位置基本符合。理论模型中由于4个刀齿间歇参与切削,因此各铣削分力曲线在一个铣削周期内有4个主峰,理论上这些峰值在一个周期内是相等的。但是,从图10和图11中铣削实验得到的铣削力曲线可以看出各峰值存在差异,其原因在于铣削过程中存在刀具跳动现象。由于实验15的切削深度与切削速度要远大于实验1,因此刀具跳动效应也随之增大,这也导致了图11各铣削分力峰值 图10 第1组实验中铣削力理论模型结果与实验结果的对比Fig.10 Comparison of milling force theoretical model results and experimental results in group 1 experiment 图11 第15组实验中铣削力理论模型结果与实验结果的对比Fig.11 Comparison of milling force theoretical model results and experimental results in group 15 experiment 波动大于图10。对于铣削过程力,可以看出模型与实验吻合较好,其中图10所示为每齿进给量为0.05 mm的切削过程,该过程中刀具的瞬时切削厚度较小,特别是切入、切出的过程中微元切削刃的瞬时切削厚度与刃口尺寸相当,此时,切削力主要由刃口作用产生,图10所示结果也进一步证明了本研究考虑刀具非对称刃口的铣削力模型的正确性。 为验证提出的模型对铣削力预测的可靠性,分别采用3种指标(皮尔逊相关系数ρ、平均误差η、峰值误差e)对模型进行评估。 (1)皮尔逊相关系数ρ (30) 式中,FS,i为理论模型中铣削分力在铣削周期中的过程力,FE,i为铣削实验中铣削分力在铣削周期中的过程力,N为一个铣削周期的切削力数据总数。 (2)平均误差η (31) (3)峰值误差e (32) 式中,maxFS为理论模型的铣削力峰值,maxFE为实验获得的铣削力峰值。 皮尔逊相关系数ρ,平均误差η和峰值误差e分别如图12所示。 由图12(a)可知,理论与实验的各组分力数据相关系数均大于0.7,表明理论与实验具有高度的相关性;由图12(b)可知,整个铣削周期中由理论所得的各铣削分力与相对应的铣削实验的平均误差均小于5%;由图12(c)可知,最大峰值误差小于15%。因此,所建立的理论模型是可靠的。 图12 理论与实验结果相关性及误差分析Fig.12 Correlation and error analysis of theoretical and experimental results 基于刀具钝化特点、金属切削理论和滑移线理论建立了刀具非对称刃口的瞬时铣削力模型,并通过铣削正交实验对模型进行验证。主要结论如下。 (1)随着微元瞬时切削厚度的不同,在刀具刃口处会经历3个不同的切削阶段:犁耕阶段、犁耕与刃口前刀面剪切同时作用阶段、犁耕-刃口前刀面剪切-刀具初始前刀面剪切同时作用阶段。 (2)在整个切削过程,随着切削厚度的增大,犁耕力所占比重逐渐减小,当进给较小时犁耕力不可忽略;在本研究设定的第1组切削参数下犁耕力的切向分力Fx、径向力分Fy的比重均在20%以上。并且,在将要切出的过程中,犁耕力的径向分力Fy所占比重具有上升的趋势。 (3)瞬时铣削力理论模型与实验数据吻合较好,并且皮尔逊相关系数均大于0.7,均值误差小于5%,峰值误差小于15%,验证了模型的有效性。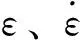

1.6 犁耕作用系数

1.7 积分区间
2 铣削力实验结果分析
2.1 铣削实验方案及实验装置

2.2 剪切力与犁耕力占比分析
2.3 理论模型与实验结果分析
2.4 模型与实验相关性及误差分析
3 结论
