基于贝叶斯BiLSTM模型的核电阀位传感器故障预警方法

游东东 黎家良 刘高俊 杨汕

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.中广核工程有限公司 核电安全监控技术与装备国家重点实验室，广东 深圳 518172)

核电是清洁、高效的能源[1]，对核电厂机械设备的运行状态进行实时监测，在设备发生故障的早期进行预警有利于及时排除故障、避免重大安全事故，而且还可以缩减设备运行成本，减少非计划性停机。

近年来，深度学习以其在特征提取与模式识别方面独特的优势与潜力，被广泛用于机械设备故障预警诊断及其它众多领域[2]。循环神经网络(Recurrent Neural Network,RNN)能够充分挖掘时间序列数据中的时序信息以及语义信息，在处理时序数据时比全连接神经网络和卷积神经网络更具深度表达能力[3]。Hadi[4]提出了一个故障检测和隔离(FDI)方法，该方法基于RNN对非线性系统进行建模和反演，建立了一个工厂预测模型，利用从模型中生成的残差来进行故障预警。Huang等[5]在他们提出的两阶段机器学习分析架构中，第一阶段运用了RNN的变分自编码器(Variational Auto Encoding,VAE)方法，提高了几种分类算法的预测精度。然而，传统的RNN在处理长时间序列的预测时，由于连乘的存在，导致梯度范数很小，常常出现梯度消失现象，当梯度范数很大时，会出现梯度爆炸现象[6]，从而削弱了训练长时间序列的记忆能力。长短时记忆网络(Long Short-Term Memory,LSTM)相比于RNN，它的整体结构没有发生太大的变化，改进之处在于隐含层，使用含有门结构的记忆单元代替隐含层中的神经元，缓解了RNN梯度消失的现象，适用于创建复杂时间序列模型[7]。Zhang等[8]提出了一种基于LSTM的轴承性能退化评估方法，综合利用了故障传播信息，最后该方法可有效地识别轴承的退化状态，准确预测轴承的剩余使用寿命。魏书荣等[9]运用LSTM预测正常工况下双馈风力发电机(DFlG)的运行温度，结果表明，该方法能提前29～72 h识别海上DFIG的早期故障。Wang 等[10]利用LSTM网络对核电厂电动阀门剩余使用寿命进行预测，结果表明，与其他典型的机器学习和深度学习方法相比，该方法能够更准确地预测剩余使用寿命。Choi等[11]利用LSTM网络预测传感器状态，在紧急情况下核电厂参数发生剧烈变化时，该模型能够基于提出的一致性指数判断传感器是否出现错误。龚安等[12]将核电设备中的主泵电机绕组温度作为研究对象，利用LSTM对其状态进行预测；实验表明，相比门控循环单元(Gated Recurrent Unit,GRU)、RNN等预测模型，LSTM对核电设备的运行状态具有更高的预测精度。

然而，现有的文献大多是关于故障诊断方面的研究，针对核电厂设备的故障预警方法不多见。本研究针对设备或传感器故障蠕变期监测与预警以及评估预测模型的可靠性问题，提出了一种贝叶斯双向长短时记忆网络(Bi-directional Long Short-Term Memory,BiLSTM)模型预测方法，利用BiLSTM对信号值进行预测，通过拟合优度和均方误差对模型进行精度验证，并用贝叶斯假设检验方法[13]对其进行不确定性分析，配合历史数据集的先验信息，使模型能够及时在机组故障蠕变期发现故障。

1 贝叶斯BiLSTM模型

1.1 特征工程

从实时数据库中提取的运行数据并不能直接用于预测模型的输入，需要进行一系列的清洗工序，包括缺失值填补[14]、小波包降噪[15]、归一化(正态化)以及降维[16]等。对于网络传输或者传感器异常造成的缺失值，常采用回归法、平均法等算法进行填补；使用小波包阈值降噪法对数据进行降噪，对于不平稳的信号有较好的效果；通过归一化处理，将数据压缩到0到1区间内，消除量纲的影响，同时便于预测模型的收敛、加快计算速度。此外，当需要用较少的维度表征大量的传感器信号时，还需要对众多的信号进行降维，去除相关性较大的信息，进而减少计算量。

从实时数据库中抽取一段健康的信号，经过以上的工序处理后得到可用于预测模型的时间序列。按照嵌入理论，等间隔取一定长度的时间序列作为预测模型每个训练单元的输入，其中间隔值为延迟时间，时间序列长度为嵌入维数。整段的时间序列被分为若干个时间段，将每段时间序列作为样本输入，将每段序列的下一个间隔值作为样本输出。采用python语言基于Tensorflow搭建预测模型，将样本分为训练集和验证集，进行交叉验证，保证预测模型具有一定的泛化能力。

1.2 BiLSTM 预测模型

RNN具有记忆功能，能够发现样本之间的序列关系，是处理时间序列的首选模型。图1为RNN结构图，图中，U是输入层到隐藏层的权重矩阵；V是隐藏层到输出层的权重矩阵；W是隐藏层上一次的值作为这一次的输入的权重矩阵。从RNN结构可知，RNN某一时刻的输出值是由当前时刻输入值和前面多个时刻的输入值共同决定的。然而，RNN模型训练过程中较常出现梯度消失现象，当输入的序列数据长度过长时，距离当前时刻较远的数据对于当前时刻的作用被削弱甚至被覆盖，造成该网络结构无法学习较远时刻的序列数据。

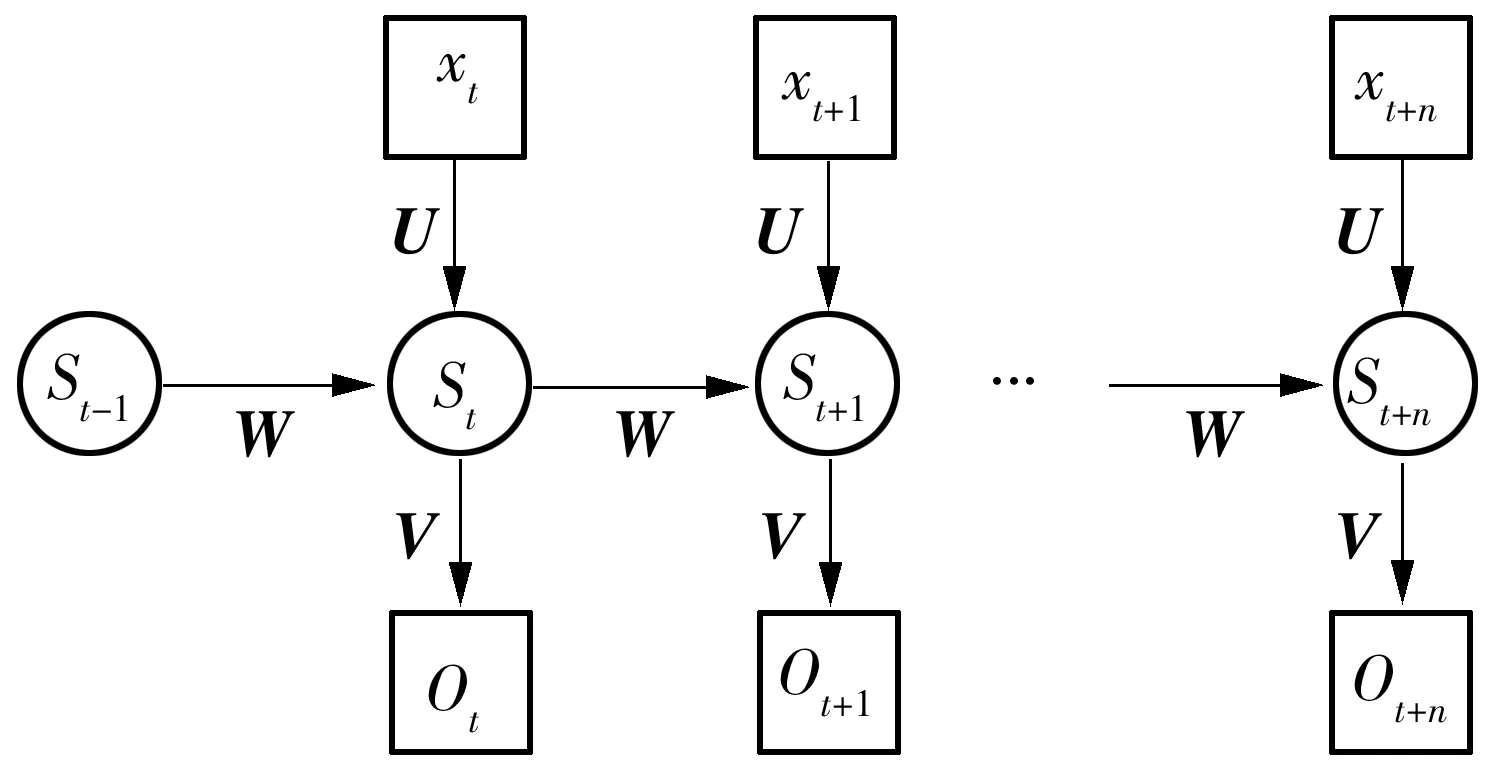
图1 RNN结构Fig.1 RNN structure

为了解决RNN结构出现的梯度消失问题，常采用RNN的改进模型中的LSTM模型，LSTM模型结构引入一种细胞状态的连接，通过引入门控单元和线性链接的方法解决梯度消失问题[17]，从而能够学习更长的时间序列。

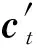
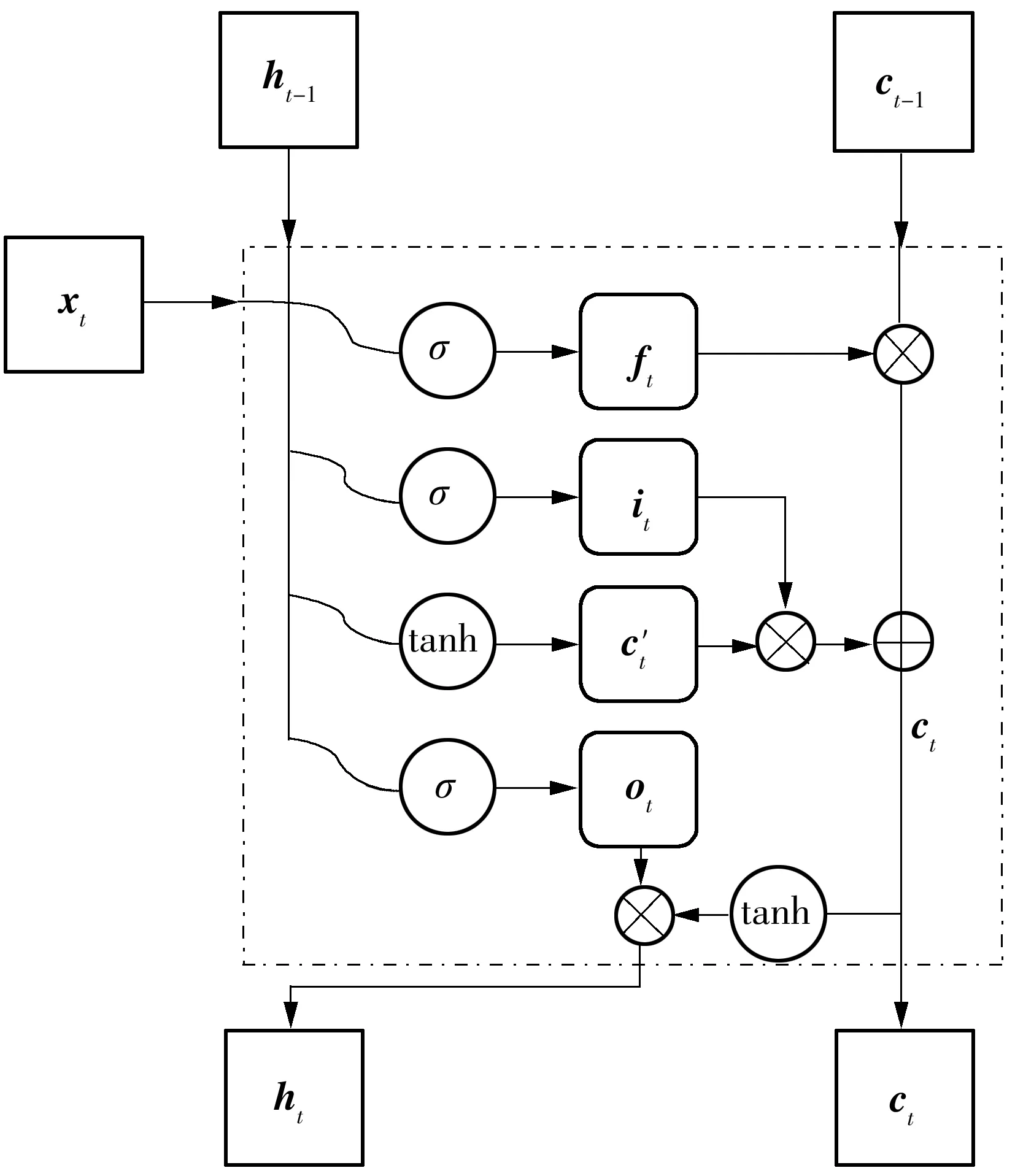
图2 典型LSTM单元结构Fig.2 Typical LSTM unit structure

ft=σ(Wf[ht-1,xt]+bf)

(1)

(2)

(3)

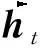
(4)

(5)

(6)

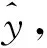
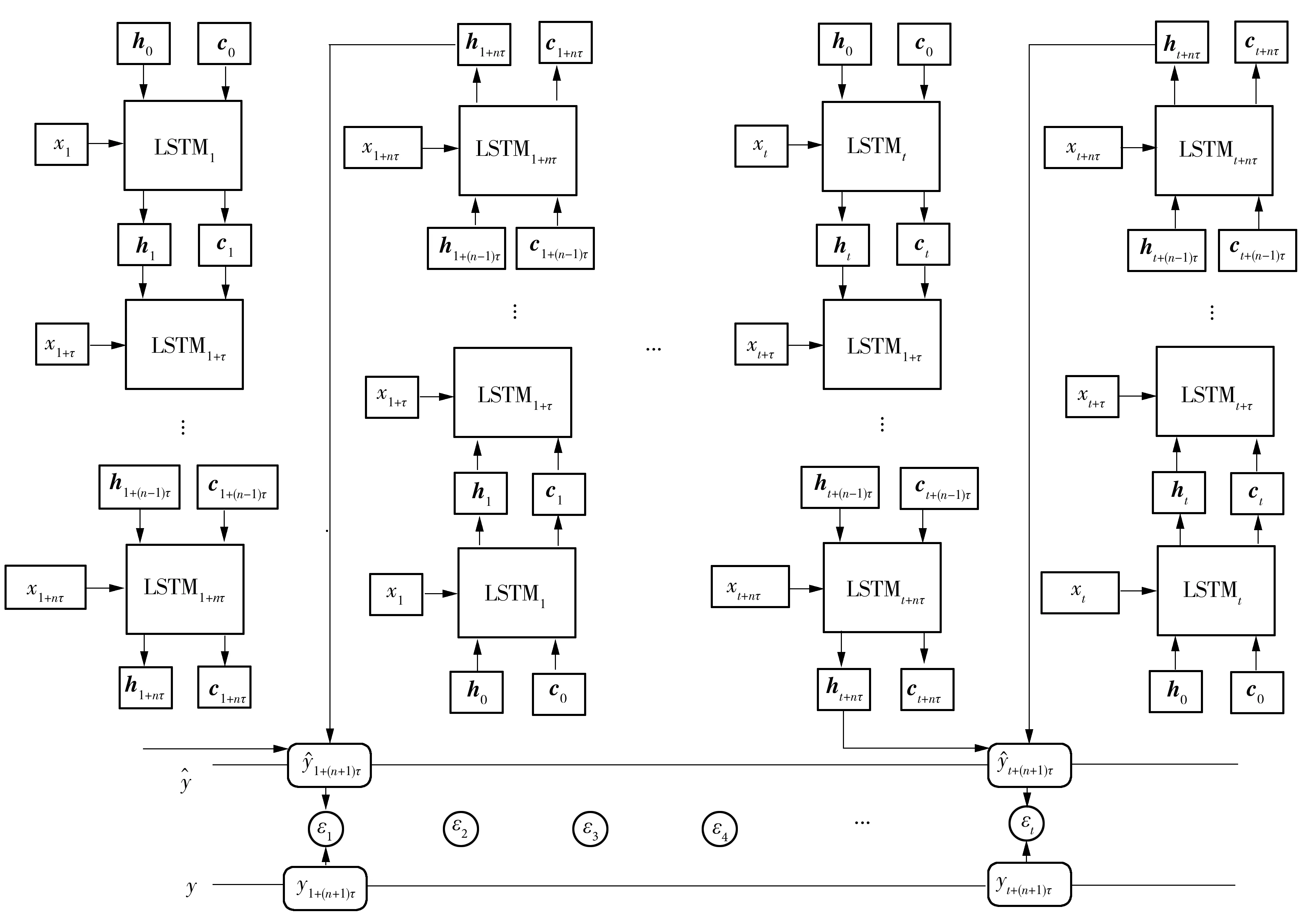
图3 BiLSTM预测模型Fig.3 BiLSTM prediction model

2 模型的验证——贝叶斯假设检验

本研究将数据集分为训练集、验证集和测试集，训练集用于搭建模型，验证集用来验证模型预测结果是否精确可靠。本研究采均方误差MSE、拟合优度R2、贝叶斯置信度这3个指标来验证模型的可靠性。对于前两个指标，当MSE的值越小、R2值越接近1时，模型的精度与可靠性就越高；然而，均方误差MSE虽然能够表明预测结果与实际结果的偏离程度，但是对于不同样本量纲的情况，其结果不具备可读性。拟合优度R2表示预测结果与实际结果的拟合程度，也表示模型相比于直接取均值的优势程度。贝叶斯假设检验方法考虑了数据的不确定性，在量化模型可靠性的同时充分考虑了训练集的先验信息。

(7)

建立待验假设H0:μ=0，备择假设H1:μ≠0。假设残差均值μ的先验概率密度服从正态分布

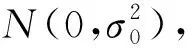
(8)

引入一个贝叶斯因子，该指标是贝叶斯假设检验的主要评价指标，它是先验概率和后验概率的比值。若贝叶斯因子显著大于1，则样本数据支持待验假设。具体公式表示为[19]

(9)

进而得到均值μ后验概率为

(10)

3 故障预警

通过设定阈值的方法来识别异常信号，达到故障预警的目的。取训练集中的最大正残差epos_max、最大负残差eneg_min记为α、β，分别为上极限阈值和下极限阈值。各时间节点的数据监测值与预测值之间的残差如(11)式所示，其中Zpos_test、Zneg_test分别为测试集的上、下残差的集合，当某时刻j的ej>α或ej<β，警报将会响起。在实时监测系统中，如果残差长时间超过所设阈值，则判断该监测对象有故障。

(11)

4 案例分析

4.1 数据采集

从国内某大型核电厂汽轮机组汽机调节系统(GRE)提取了中压缸调节阀的阀位温度传感器监测的实时温度数据用来解释整个算法流程，图4所示为BiLSTM算法流程。GRE通过调节汽轮机进汽阀开度对机组进行转速、功率、频率和压力控制，并对机组的负荷和转速实施超速、超加速、负荷速降和蒸汽需求限制，通过配套的监测系统来监视其运行，使机组安全和经济地运行与各种工况，满足运转要求。然而现有的GRE发出警报时，意味着该机组停机，这将会造成运行成本的增加。本研究将利用BiLSTM预警模型监视汽轮机调节阀温度信号，在系统故障蠕变期间预警。

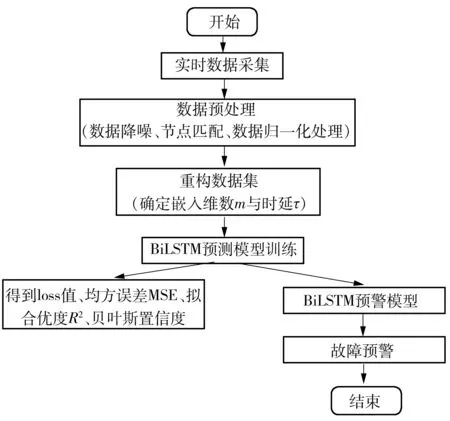
图4 BiLSTM算法流程Fig.4 Flow chart of BiLSTM algorithm

数据集跨度为2018年7月16日0:00至2018年10月1日0:00，将7月16日0:00至8月20日0:00作为训练集训练BiLSTM预测模型的各个超参数、权值与偏置，将8月20日0:00至8月30日0:00作为验证集验证模型可靠性，将8月30日0:00至10月1日0:00作为测试集预测故障节点。

4.2 重构数据集

采集的实时数据是一维的长序列数据集，如果直接将该数据集输入到BiLSTM预测模型进行训练，会严重影响预警精度，达不到理想的预警效果，所以需要对数据进行预处理。图4中，在进行预处理后，仍然是一维的长序列数据集。这时，对数据集进行重构，根据均方误差MSE和拟合优度R2确定嵌入维数m和时延，以得到精度最高的预警模型。

如图5所示，图5(a)、5(b)为不同时间延迟下训练集与验证集的拟合优度R2与均方误差MSE的值。由前文所述可知,R2越接近1、MSE越小，证明模型的精度越高，因此由图5(a)、5(b)可得，当=1,2,3时，模型精度较高，为了预测更远未来的时间节点，初步拟定=2，3。图5(c)、5(d)为=2条件下，不同嵌入维数的拟合优度R2和均方误差MSE的值，由图示结果可知，模型精度随着嵌入维数m的增加呈先增后减的趋势，在m=4,5时达到最优值。

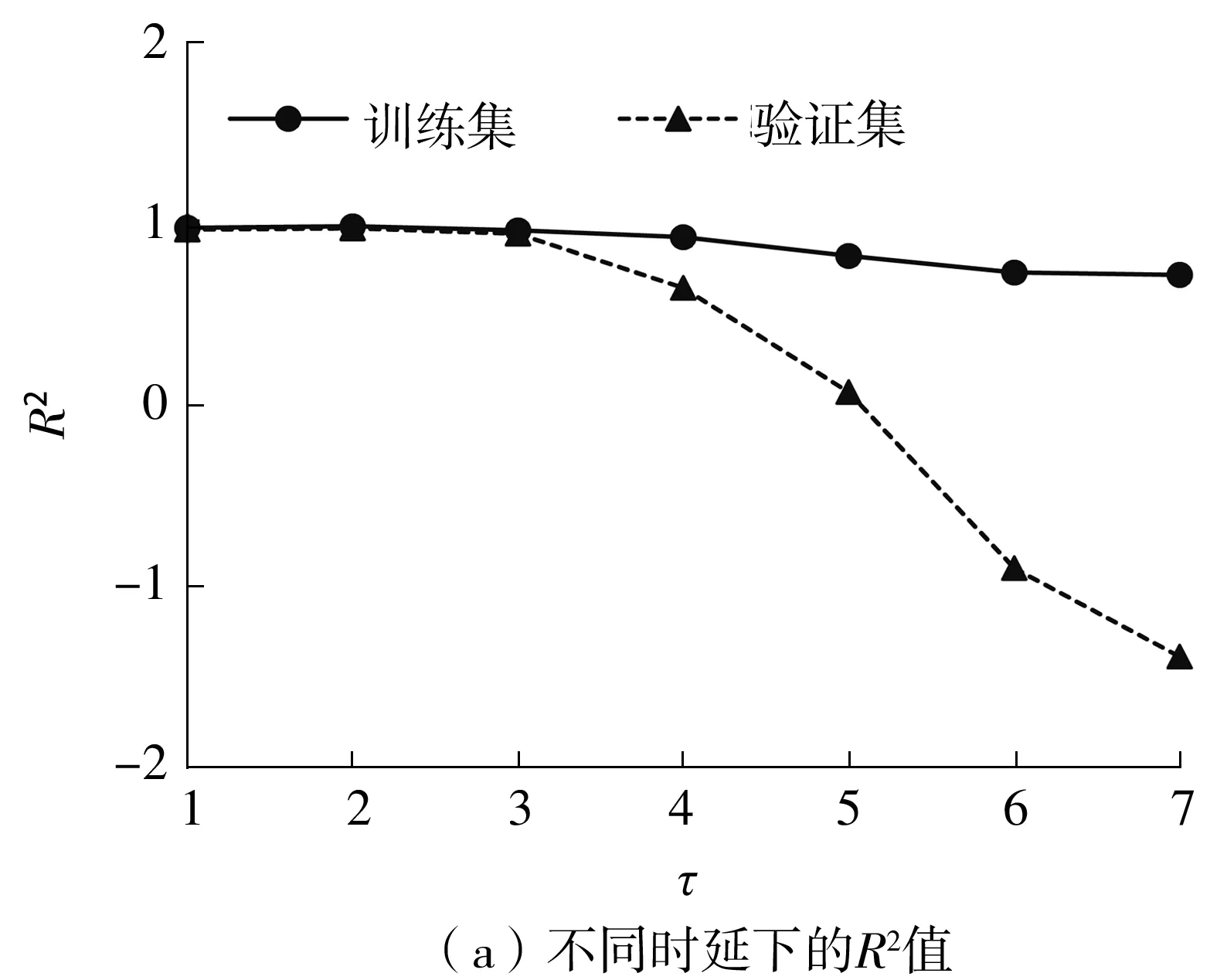
图5 不同嵌入维数与时延下的MSE与R2的值Fig.5 Values of MSE and R2 under different embedding dimension and delay

4.3 贝叶斯BiLSTM预警模型训练

温度源数据集中共有1 827个时间节点，其中训练集有833个时间节点，验证集有233个时间节点，测试集有761个时间节点。一般而言，预测模型能够预测多远的时间节点，取决于时延的大小。为了进一步确定m和，对BiLSTM和LSTM的预测模型进行不同嵌入维数与时延下的训练，其内部隐藏层的大小为49，权重初始化方法为均匀初始化器方法lecun_uniform，它是一种基于uniform的方法，从[-limit,limit]区间均匀采样作为权重初始化参数，其中limit=sqrt(3/fan_in)，fan_in是权重张量中的输入单位的数量。训练结果如表1所示，由表1可见，当m=4、=2时,BiLSTM模型与LSTM模型相差不大，然而=3时，前者精度均明显优于后者，为了预测更远的时间点，拟用m=4、=3这一组合。

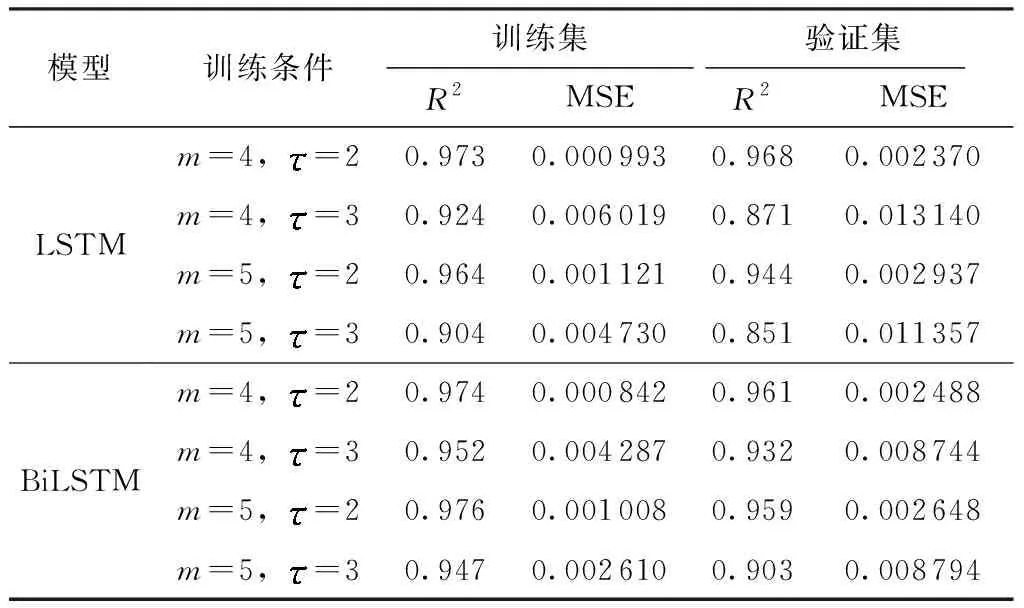
表1 BiLSTM和LSTM在不同嵌入维数与时延下，训练集和验证集的拟合优度R2和均方误差MSETable 1 Goodness of fit R2 and mean square error MSE of training set and verification set of BiLSTM and LSTM under different embedding dimensions and time delays

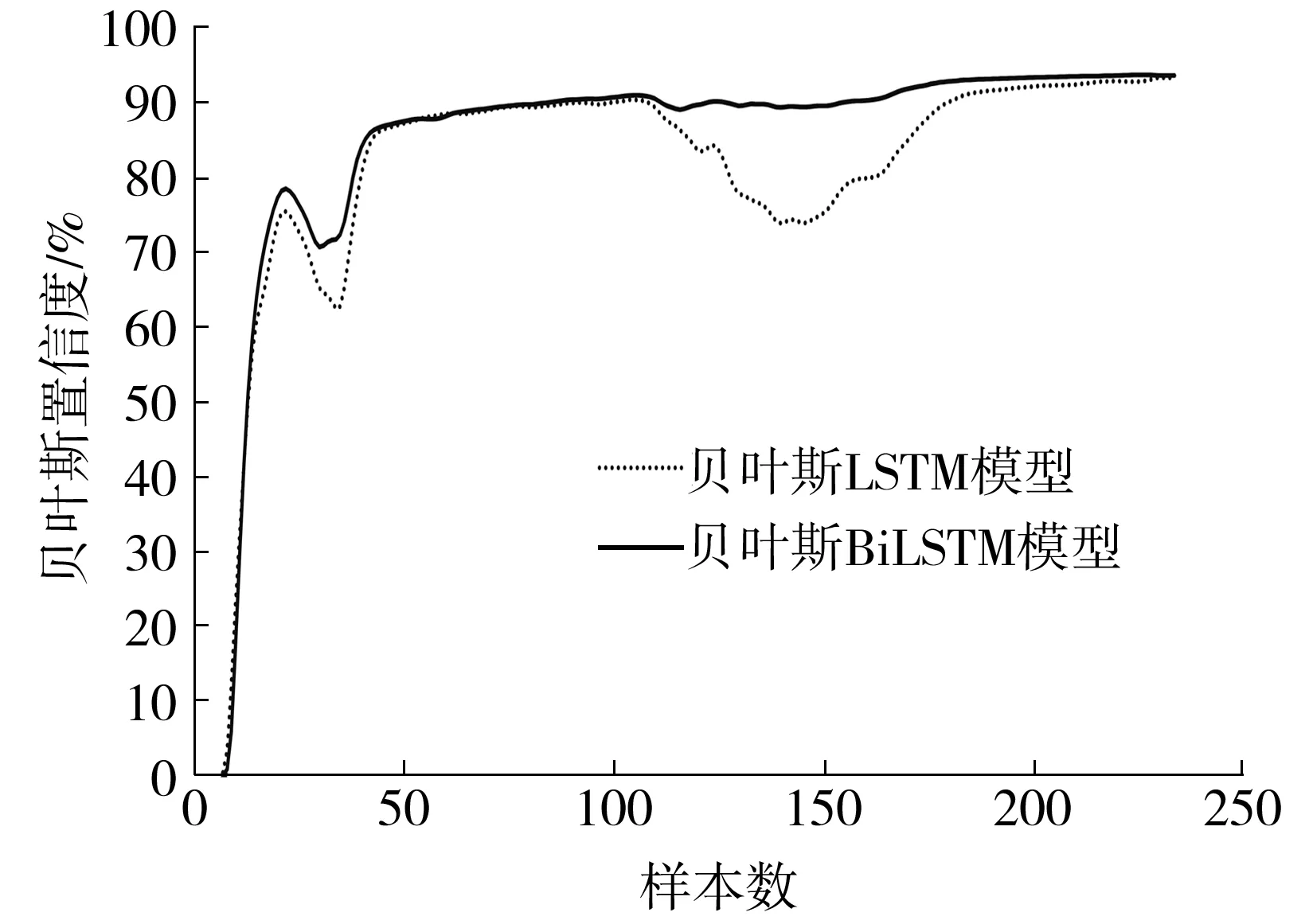
图6 验证集的贝叶斯置信度Fig.6 Bayesian confidence of verification set

图7所示为预测效果图，图中，纵坐标表示经归一化、无量纲化后的温度值，红线为贝叶斯BiLSTM模型，绿线为贝叶斯LSTM模型。由图7可见，在两个灰色框中，红线比起绿线更接近黑线，意味着贝叶斯BiLSTM的预测效果比贝叶斯LSTM的预测效果更好。综上所示，文中提出的贝叶斯BiLSTM在考虑数据不确定性的情况下，预测效果更优秀。

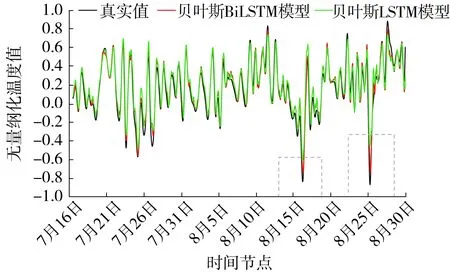
图7 训练集和验证集的预测效果图Fig.7 Prediction effect chart of training set and verification set

4.4 故障预警——案例1

为了验证预警模型的预警能力，用前文4.3节中创建的贝叶斯LSTM预警模型来预测测试集的数据，然后将预测值与真实值作残差，得到残差值。采用设定阈值的方法来识别异常信号，将训练集中的最大正残差和最大负残差作为识别异常信号的阈值。

测试集的预警效果如图8所示，其中红色实线为预警线，两条预警线之间的区域为安全区域，安全区域之外为警报区。由红色圆点得知，经贝叶斯BiLSTM预警模型得到的测试集有3个预警报点以及3段长警报区段。故障节点统计结果如表2所示，由表2可见，预报警点分别是8月30日13:00、9月8日11:00、9月23日12:00，均比实时监控系统提前15 h以上，而且结合图8可见，在每个预警点之后一段时间里，残差一直超过所设的预警线，由此可初步得到，汽轮机组阀位处存在安全隐患。查阅该数据集配套的资料确认故障点为阀位传感器故障，故障原因是该阀位传感器供电滤波电容故障，导致传感器的检测温度数据出现异常，使得该预测模型一段时间处于警报区，一段时间又回归正常；累积两次后，一次是①号警报点，另一次是②号警报点，最终在2018年9月24日02:04时，主控触发，阀位传感器异常关闭。上述证明，贝叶斯LSTM预警模型能提前预测实时监控系统的报警。

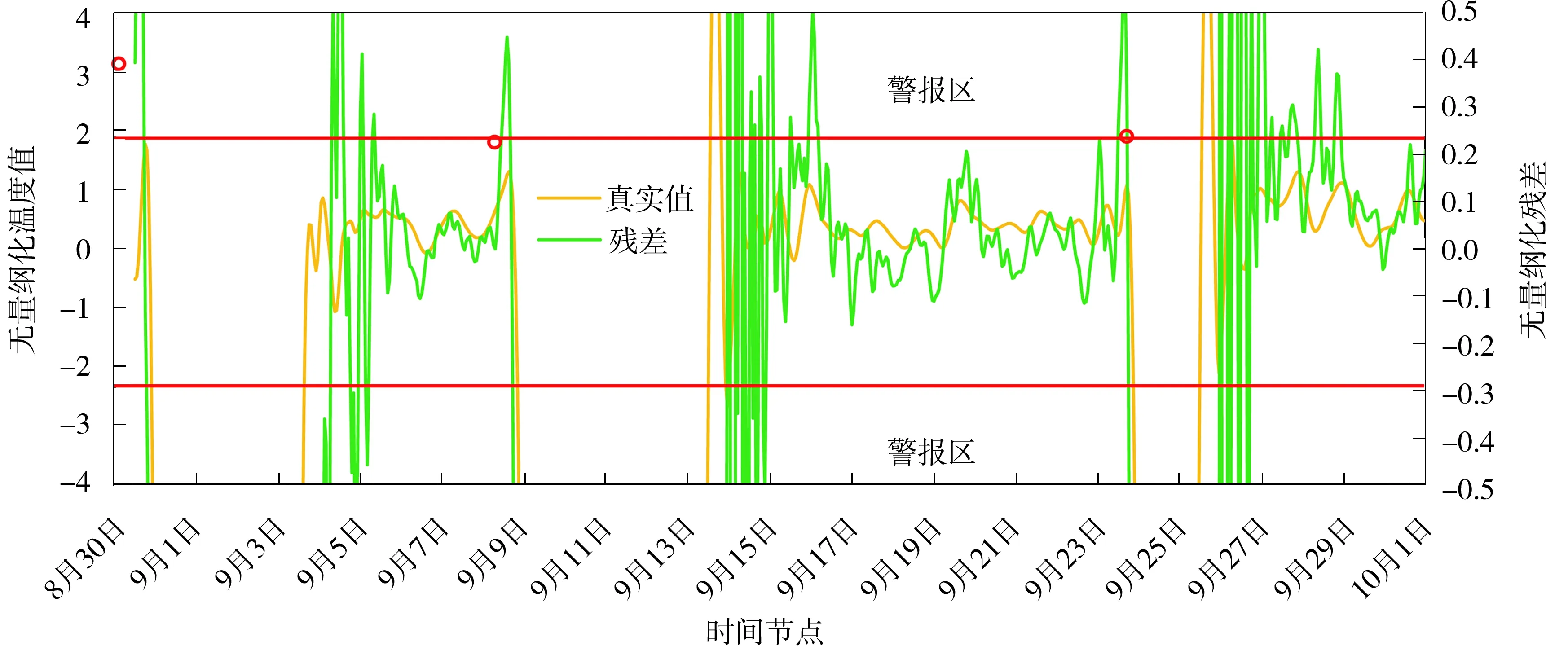
图8 “案例1”测试集的预警效果图Fig.8 Early warning effect diagram of “case 1” test set

表2 “案例1”故障节点统计表Table 2 Statistics of “case 1” fault nodes

4.5 故障预警——案例2

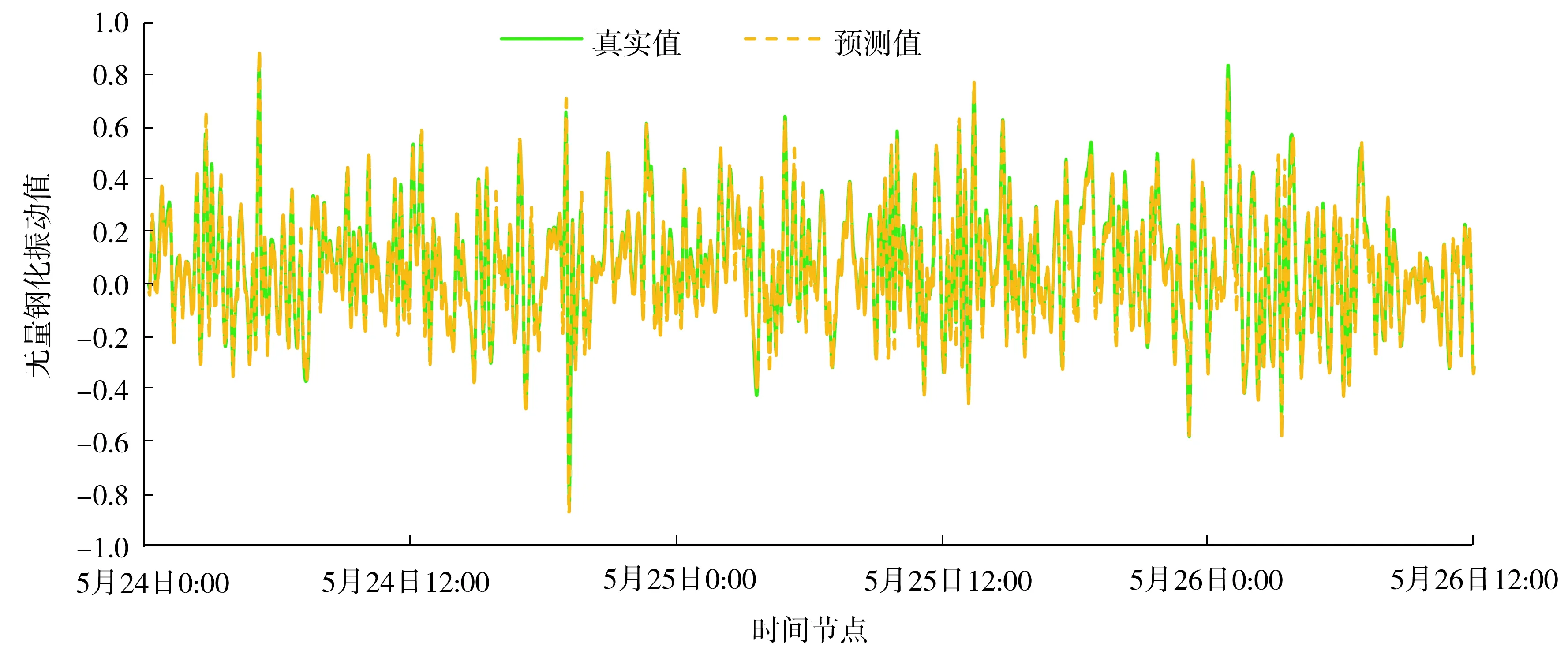
图9 “案例2”训练集与验证集的预测效果图Fig.9 Prediction effect diagram of “case 2” training set and verification set

“案例2”测试集的预警效果图如图10所示，红色为预警线，其值分别为α和β。经贝叶斯BiLSTM预警模型得到的测试集有2个预警报点以及2段长警报区段。如表3所示，它们分别是5月26日20:12、5月27日03:41，均比实时监控系统提前，并在报警后相当长的一段时间内持续发出警报，由此可初步得到，该机组泵驱动端轴承存在安全隐患。查阅该数据集配套的资料，在2018年8月29日13:31对该泵解体时发现故障原因为泵首级叶轮流道有一磨头遗留。上述证明，贝叶斯LSTM预警模型能提前预测实时监控系统的报警。

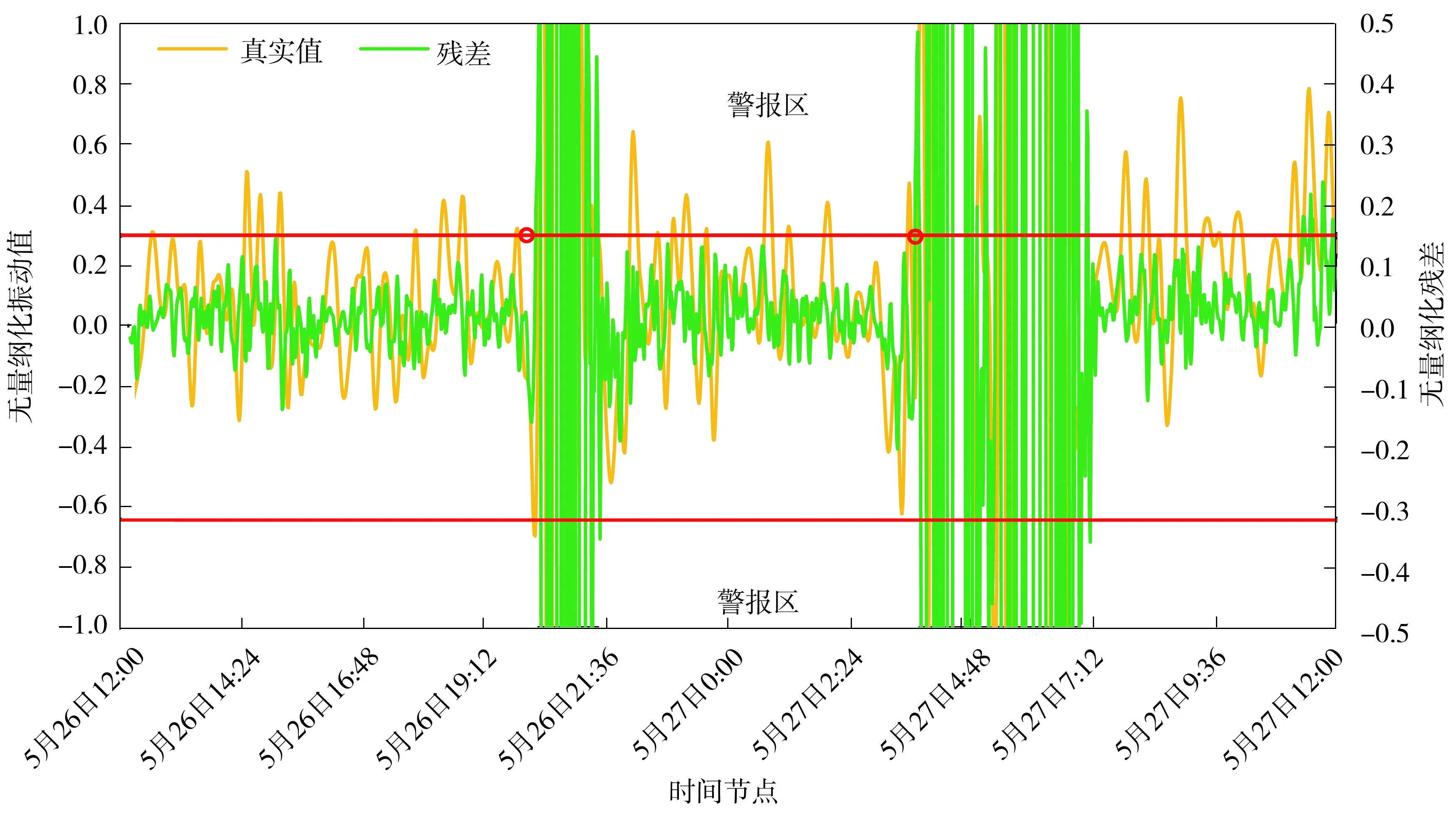
图10 “案例2”测试集的预警效果图Fig.10 Early warning effect diagram of “case 2” test set

表3 “案例2”故障节点统计表Table 3 Statistics of “case 2” fault nodes

5 结论

针对大型核电机械设备故障蠕变期监测与预警以及评估预测模型的可靠性问题上，提出了基于贝叶斯BiLSTM的故障预警方法。源数据集经过预处理、重构后，得到降噪重构的数据集。然后建立了BiLSTM预测模型，训练集与验证集的数据经过BiLSTM预测模型训练后，在嵌入维数m=4与时延=2时，拟合优度均大于0.96，均方误差在0.001这个数量级。值得注意的是，当m=4、=3时，BiLSTM模型的预测精度比LSTM更优，证明了BiLSTM预测模型具有更好的预测能力以及可靠性。此外，文中还提出了基于贝叶斯假设检验的方法，考虑数据不确定性和训练集的先验信息，对模型的置信度进行量化分析，结果表明贝叶斯置信度在93%以上，进一步验证了模型的可靠性。

在模型可靠的基础上，将此模型用于设备的故障预警，运用硬阈值预警法，将训练集的最大正残差和最大负残差作为报警阈值，当测试集某个时间节点超过该阈值时，贝叶斯LSTM预警系统会发出警报，经实验得知，文中提出的方法相比于现有的实时监测系统，其发出警报的时间均有提前，证明其具有良好的预警效果。