流延薄膜传热特性及冷却水量设计的仿真研究
2022-01-29殷术贵郭伟科黄栋张华伟吴后吉张春华
殷术贵 郭伟科† 黄栋 张华伟 吴后吉 张春华
(1.广东省科学院智能制造研究所 可靠性与装备技术中心,广东 广州 510650;2.广东仕诚塑料机械有限公司,广东 佛山 528225)
挤出流延是薄膜生产的主要方式,原料树脂热熔后从挤出机的模头挤出,熔融树脂经机头流延到表面光洁的冷却辊上迅速冷却成薄膜,经厚度测量、电晕处理、切边,牵引收卷成膜;因具有设备工艺简单、可连续生产、产品缺陷小、性能均一、生产效率高等优点,流延法生产的薄膜占薄膜总量的35%以上[1- 3]。随着新技术、新工艺、新设备、新材料的运用,流延薄膜产品越来越多样化,有高温蒸煮膜、低温热封膜、真空镀铝膜、高亮度热封膜、增韧膜、镀铝膜、易撕膜等,并广泛应用在食品包装、日用品包装、医药用品、纺织品等领域[4- 5]。
目前国外薄膜生产技术较为成熟,流延机组生产稳定可靠,利用现代挤出技术,流延线速度可达到600 m/min,薄膜宽幅达到7m[6],极限拉伸比超过400%,最小薄膜厚度12 μm;而在1985年,极限拉伸比仅为200%、最小薄膜厚度为25 μm[7]。早在19世纪80年代,W.米敏利等[8]就根据薄膜挤出流动规律,总结了各类流延模具结构尺寸的经验设计方法,并对比分析了其优缺点与适用场合。之后很多学者开始利用各种分析方法对流延生产设备进行设计优化。Smith等[9- 10]采用两种有限元算法(欧拉(E)法和校正拉格朗日(UL)法)对流延膜进行模拟对比分析,研究表明,对于一维简单流延膜仿真可以采用E算法,对于二维复杂问题应采用UL算法。Snigerey[11]采用柱型阶梯流道模型分析了塑料溶体喷出时的速度分布情况,研究了不同加热情况下出口位置的压力场、应力场和温度场分布。Ju等[12]联合随机拉格朗日欧拉法与脊柱法对薄膜自由表面进行追踪,通过对黏弹性流体流动过程的模拟,得到了二维流延薄膜动力学的瞬态解,成功地刻画了牵引共振、颈缩和边缘发展3种不稳定模式下的基本流动行为。Sollogoub等[13]为了获得薄膜自由表面,在聚合物熔体周围引入了一种虚构的流体,计算各种加工条件、传热条件和黏弹性下的颈缩和薄膜轮廓。Sanket等[14]基于单一模态和多模态PTT本构方程的线性稳定性分析方法,对流延薄膜挤出过程进行了稳定性分析,研究了单模态和多模态的弛豫效应。
早期国内流延薄膜全依赖引进设备进行生产,20世纪末逐步开展流延成型技术的研究,21世纪得到蓬勃发展,很多品种薄膜的生产都取得了长足进步[15]。李钢等[16]对双向回流式流延辊的换热过程进行了数值模拟,研究了流道结构、尺寸等参数对流延辊换热能力的影响。笔者所在课题组在前期研究中提出了在流延辊出水腔添加导流叶片的优化方案,提高了流延辊的送水能力[17]。 Zheng等[18- 19]主要对模唇到流延辊之间的薄膜形状进行研究。李晓伟等[20]认为塑料薄膜内温度均匀,是一个热量随时间变化的零维热源,对流延法生产塑料薄膜的传热过程进行了数值模拟,得到流延辊内壁温度分布及塑料薄膜温度随时间的变化曲线。李福森等[21]认为流延膜在宽度方向上的温度变化很小,可以认为宽度方向上温度分布一致,以此对双向回流式螺旋流道的流延辊的换热过程进行了数值模拟,得出了流延辊内部流道结构、冷却水流量对流延辊换热强度的影响趋势。吴哲浩等[22]认为流延膜和流延辊的传热过程是稳态传热,并对平行流道结构流延辊冷却薄膜的过程进行数值模拟,模拟的最小膜厚度为100 μm,得到了不同流延膜厚度和流延辊转速条件下流延膜的温度场分布;同时研究得出,薄膜沿宽度方向的温度分布为一平滑曲线,曲线中间高两端低。Li等[23- 24]对辊筒外表面热流采用二维模拟,随后将二维热量仿真结果带入三维结构再进行二次仿真。
从上述文献可知,国内学者对薄膜冷却传热仿真进行了许多简化,能仿真薄膜及辊筒大体温度分布情况,但微观信息特点难以捕捉。国外学者主要研究薄膜从上游模头出口被拉伸到流延辊表面之间的过程,而对薄膜与辊筒的传热模拟研究较少。由于薄膜流延过程成型机理较为复杂,采用理论分析、实验研究与数值模拟相结合的方法成为一种趋势,通过采用适当的研究方法,可以在流延产品的产量及质量方面获得大幅度提升,本研究提出了一种新的塑料薄膜与流延辊换热研究方法,并借助Fluent软件对薄膜冷却过程进行了仿真研究。
1 流延薄膜传热仿真模型
1.1 几何模型
流延膜的冷却成型过程主要发生在流延辊上,流延辊是直径较大的钢辊,内部中空设有内套,内套上焊有螺旋形的导流片,钢辊、内套、导流片之间的空间形成冷却水流道,冷却水从X正向流入、负向流出,如图1所示,其中薄膜宽度2.8 m,流延辊外筒直径0.6 m。
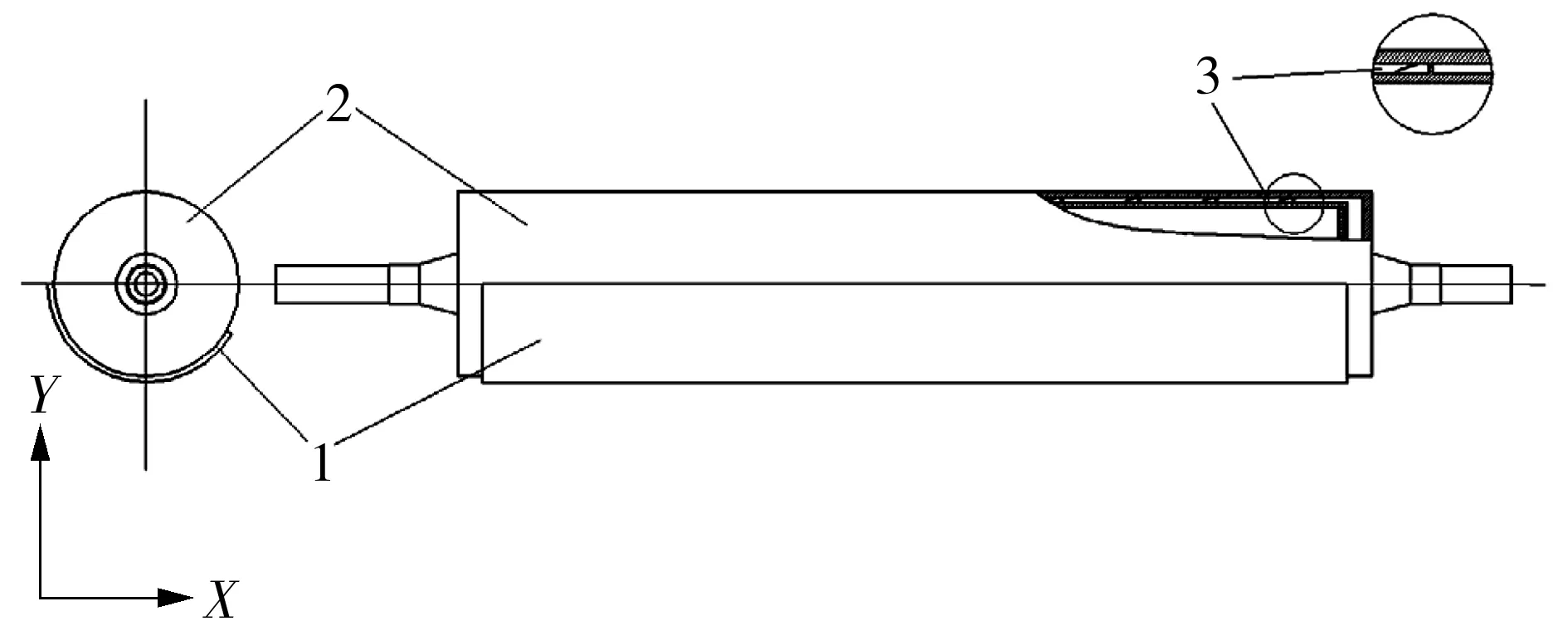
1—流延辊;2—流延薄;3—冷却水流道
1.2 数学模型
描述流体动力学控制方程的通用形式为

(1)
展开形式为
(2)
式中:φ是通用变量,可以代表u、v、w、T等求解变量;Γ是广义扩散系数;S为广义源项。
式(1)各项依次为瞬态项(Transient Term)、对流项(Convective Term)、扩散项(Diffusive Term)和源项(Source Term)[25]。本仿真模型采用标准的k-ε模型,对应的在三维直角坐标系下具体形式如表1所示。

表1 标准k-ε模型控制方程中各符号的具体形式[25]Table 1 Specific expressions of symbols in stand k-ε general control equations[25]
1.3 薄膜模型
流延薄膜在实际生产过程中,薄膜厚度为微米级,长度/宽度为米级,如果采用真实的几何模型,如流延薄膜尺寸宽幅为2.8 m、厚度20 μm、薄膜包角为150°时,流延辊面上薄膜长度约为0.8 m,取厚度方向划分5个网格,长宽比不超过20,则这一薄膜的网格数量为
(3)
上述网格数量还仅仅是薄膜的个数,其数量级达到十亿级别,再加上流延辊、冷却水流道部分的网格,网格数量将在此基础上成十倍、百倍量增加,网格数量巨大,数值计算非常困难。
为了规避上述由于网格数量巨大带来的问题,研究人员在对薄膜流动传热进行研究时,要么回避薄膜的仿真研究,要么进行一定的简化处理,如将瞬态问题转化为稳态进行模拟、将真实三维几何模型转换为二维甚至一维问题进行模拟、将薄膜的一维或二维仿真结果作为边界条件施加到三维模型上,然后再进行三维仿真模拟等,这些简化的处理方法对薄膜的仿真研究有一定的可取之处,能够大体模拟出流延膜、流延辊的温度场分布情况,但微观信息难以捕捉。此外,文献[23- 24,26- 27]有类似流延薄膜过程的非晶带材成形冷却模拟,但非晶带宽度远小于流延薄膜宽度,网格数量已然很小,但也会进行间接仿真,如用特定的热流密度,分步模拟等方式对非晶带冷却过程进行模拟。
本研究提出了一种流延膜与流延辊换热的仿真研究方法,即对薄膜进行加厚处理,增厚的薄膜,网格数量急剧降低,具体实现步骤如下。
1)分别建立流延膜、流延辊、冷却水流道三维几何模型。其中流延薄膜的厚度尺寸增大M倍,长度及宽度尺寸与实际尺寸按1∶1的比例建模,如图2所示。流延辊和冷却水流道与实际尺寸1∶1的比例建模。对于本流延薄膜模型,实际膜厚度为0.02 mm,增厚以后的薄膜厚度为20 mm。
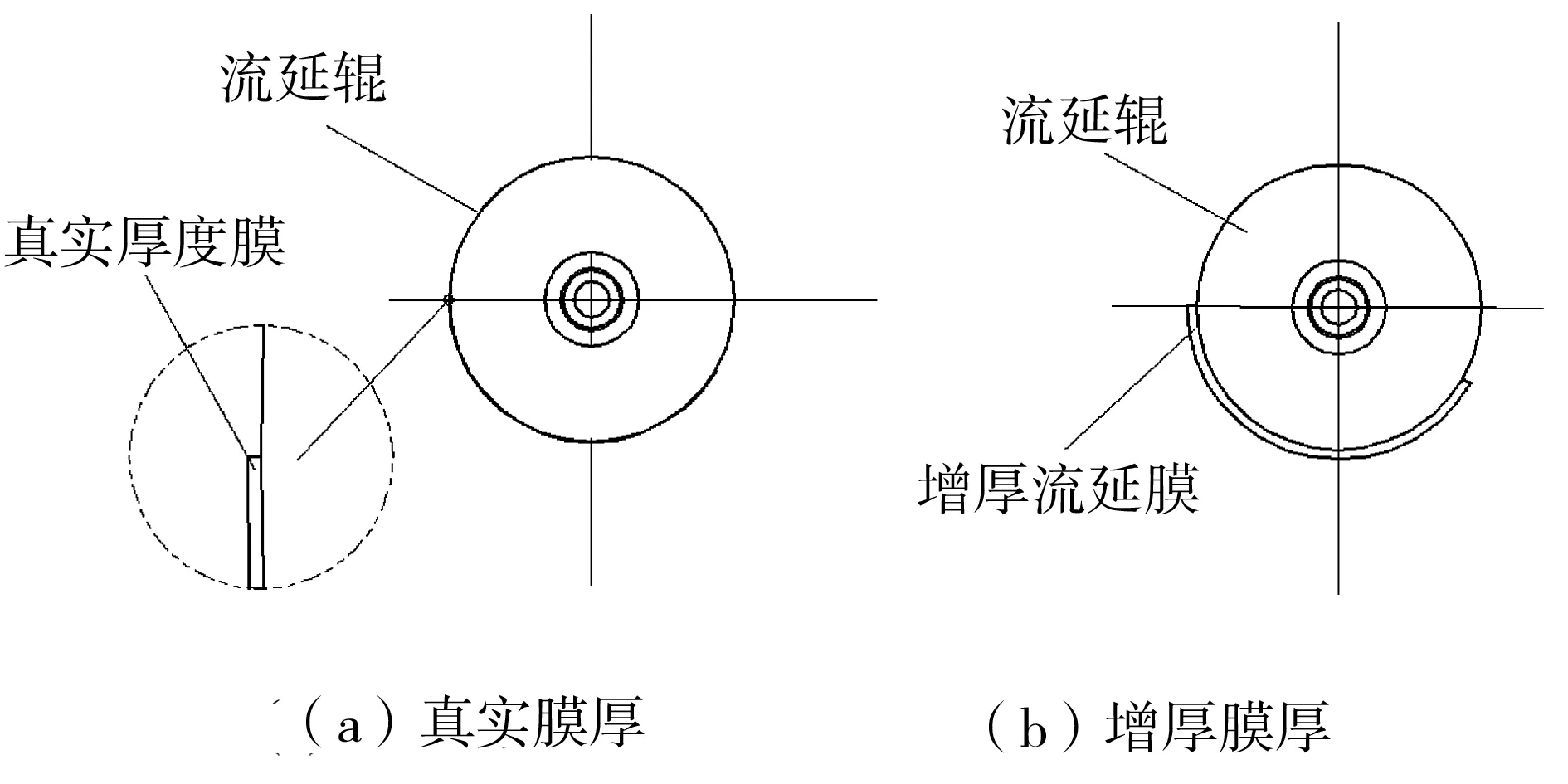
图2 薄膜增厚模型Fig.2 Film thickening model
2)分别对流延膜、流延辊、冷却水流道进行网格划分,由于流延薄膜进行了加厚处理,则流延膜长宽比得以降低,整体网格数量极大降低。
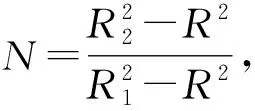
(4)


1.4 网格划分及网格独立性检查
对流延薄膜采用六面体网格划分,流延辊及冷却水流道采用四面体网格划分,网格划分结果如图3所示。网格独立性检查的目的是为了保证数值模型准确的前提下尽可能地减少计算量,起到节约计算资源的效果。本研究共选取了5组网格进行网格独立性验证,采用标准的k-ε模型,近壁区用标准壁面函数处理黏性底层问题,冷却水流道入口条件为速度入口,出口为压力出口,进口速度0.6 m/s,湍流强度4.2%,水力直径75 mm;出口压力0.1 MPa,湍流强度4.2%。以出口质量流量为参考指标进行比较,结果如表2所示。

图3 网格划分Fig.3 Mesh of the geometric
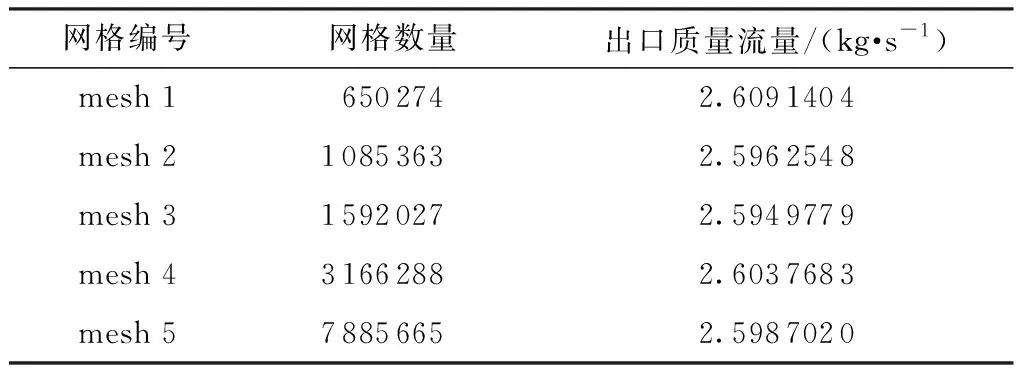
表2 不同网格数量下出口质量流量Table 2 Outlet mass flow under different grid numbers
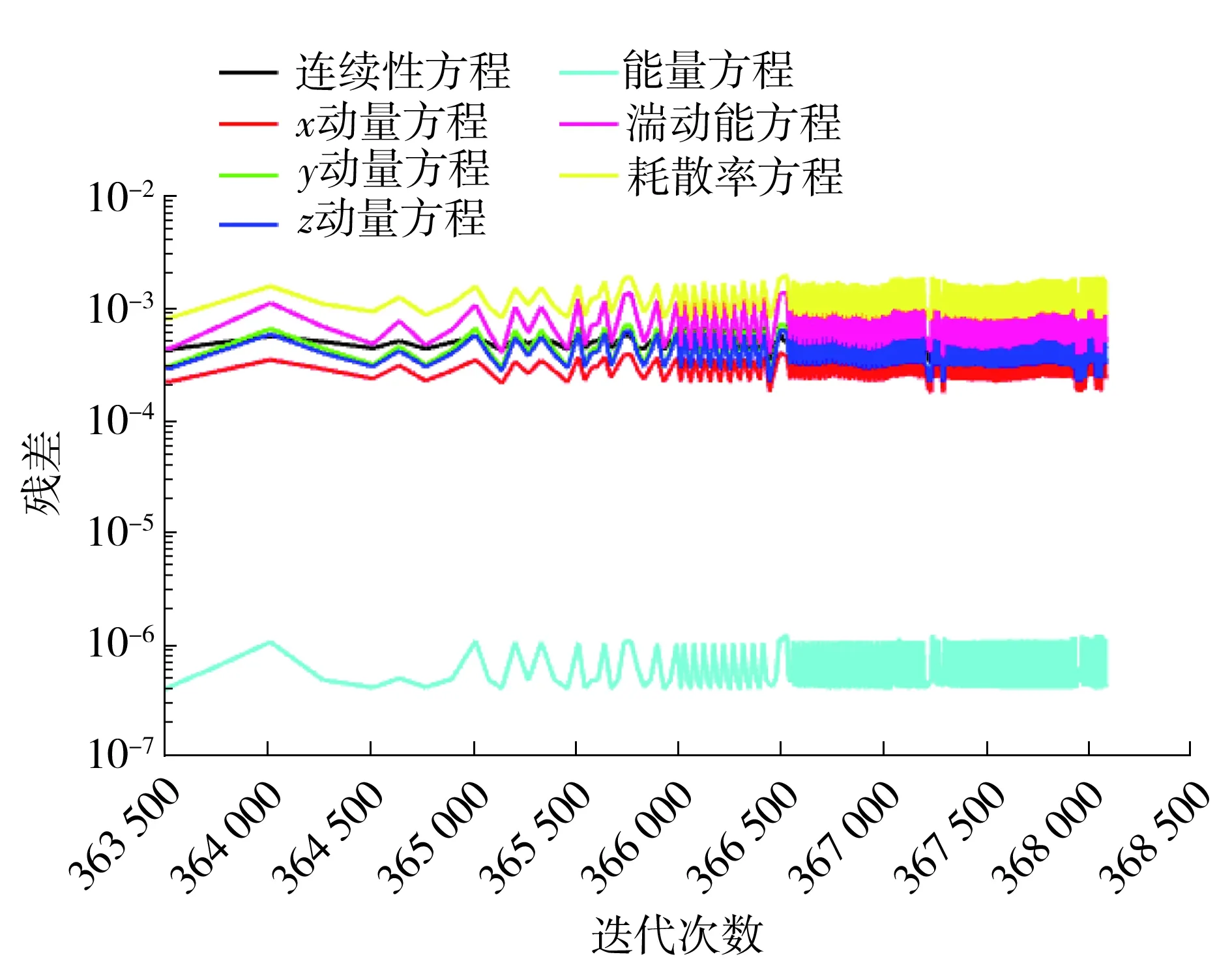
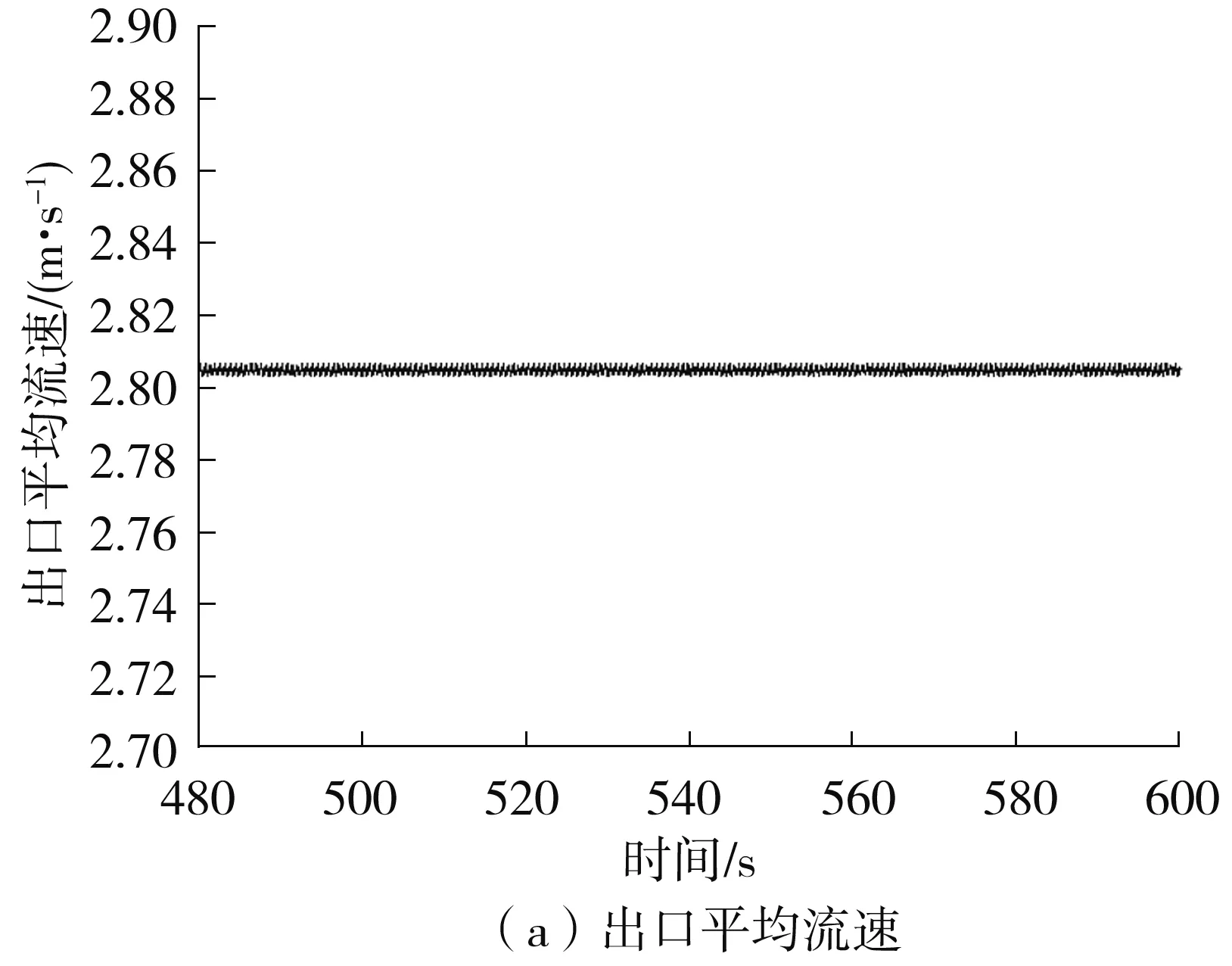
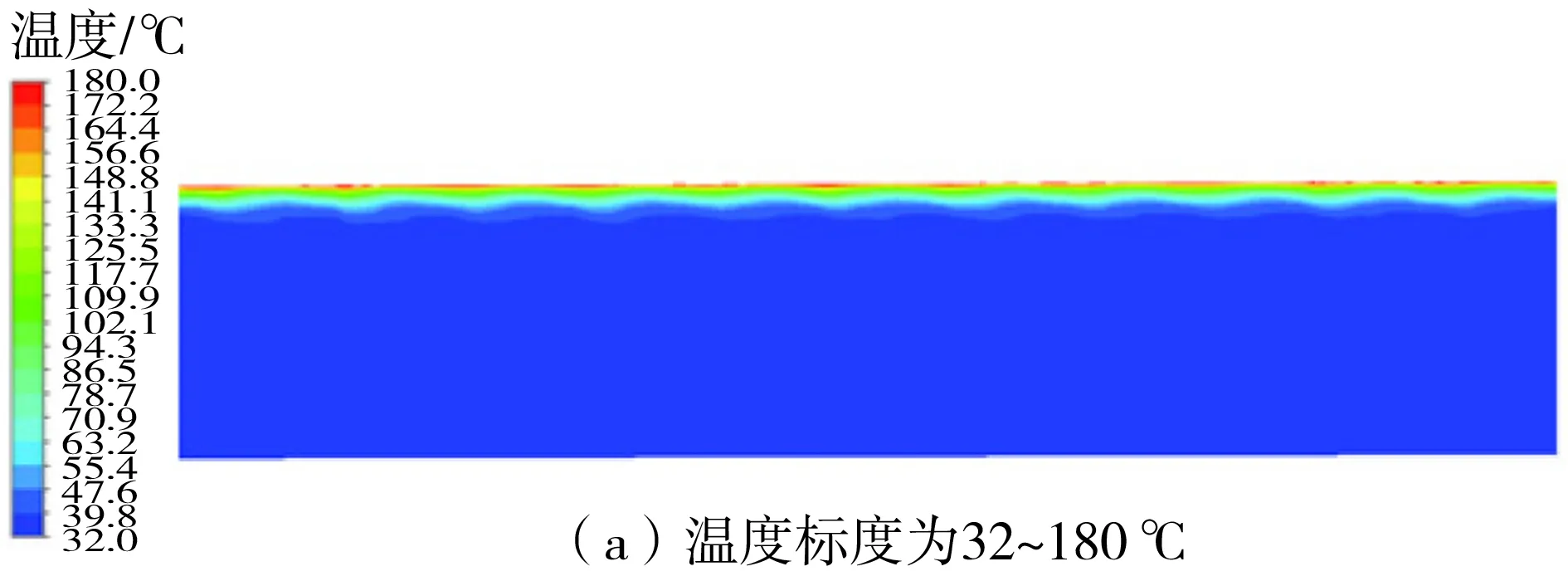
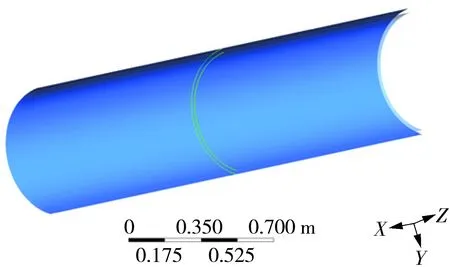
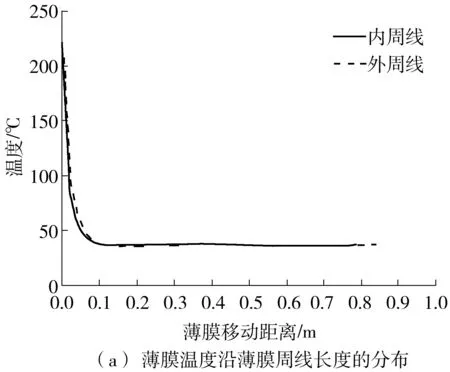
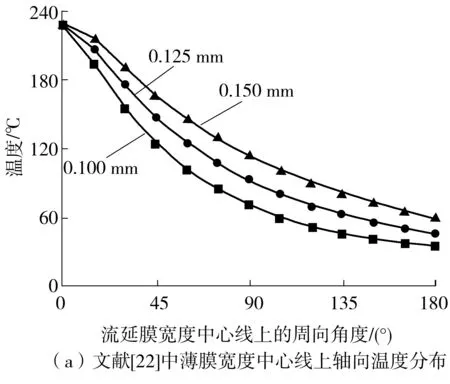
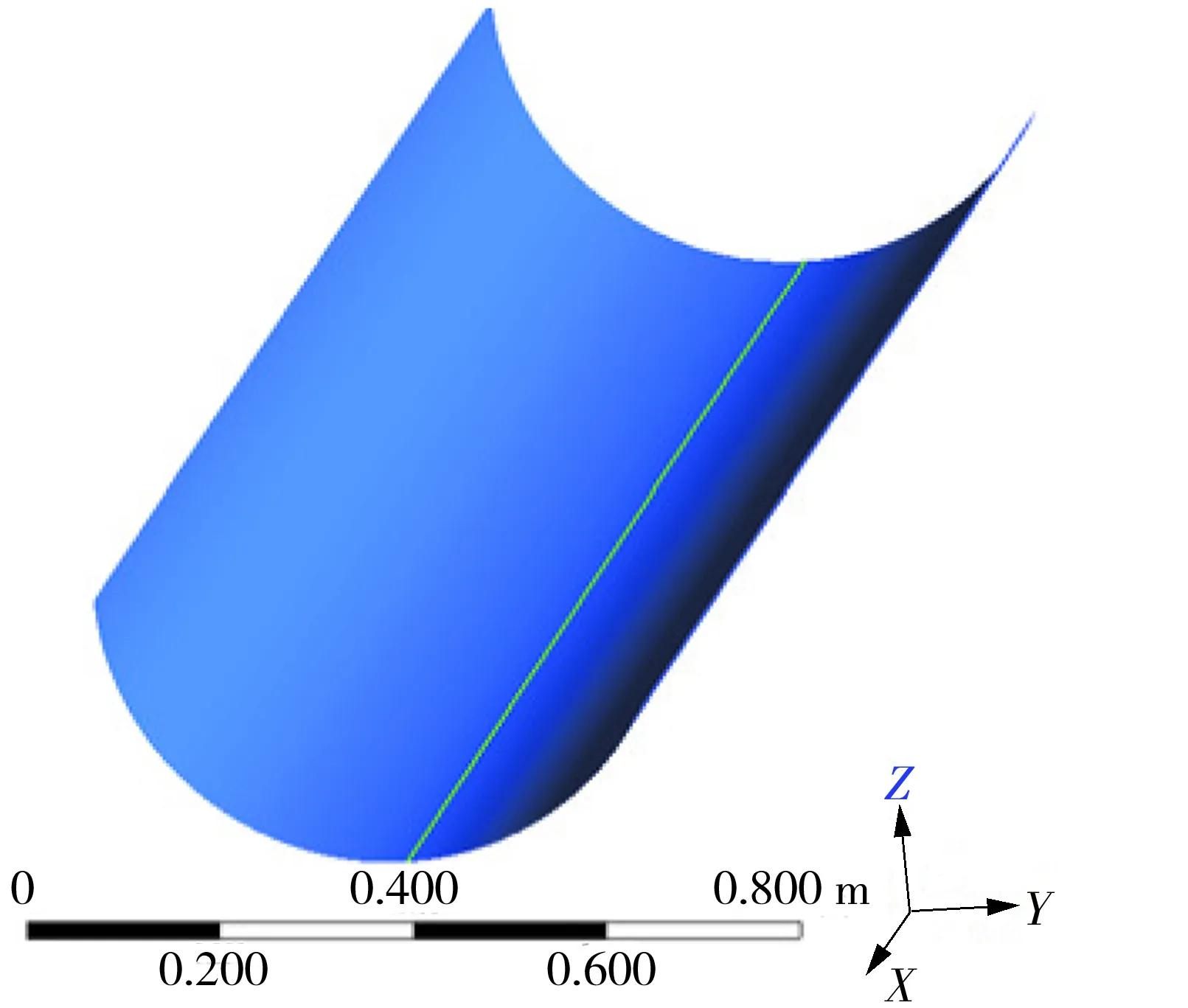
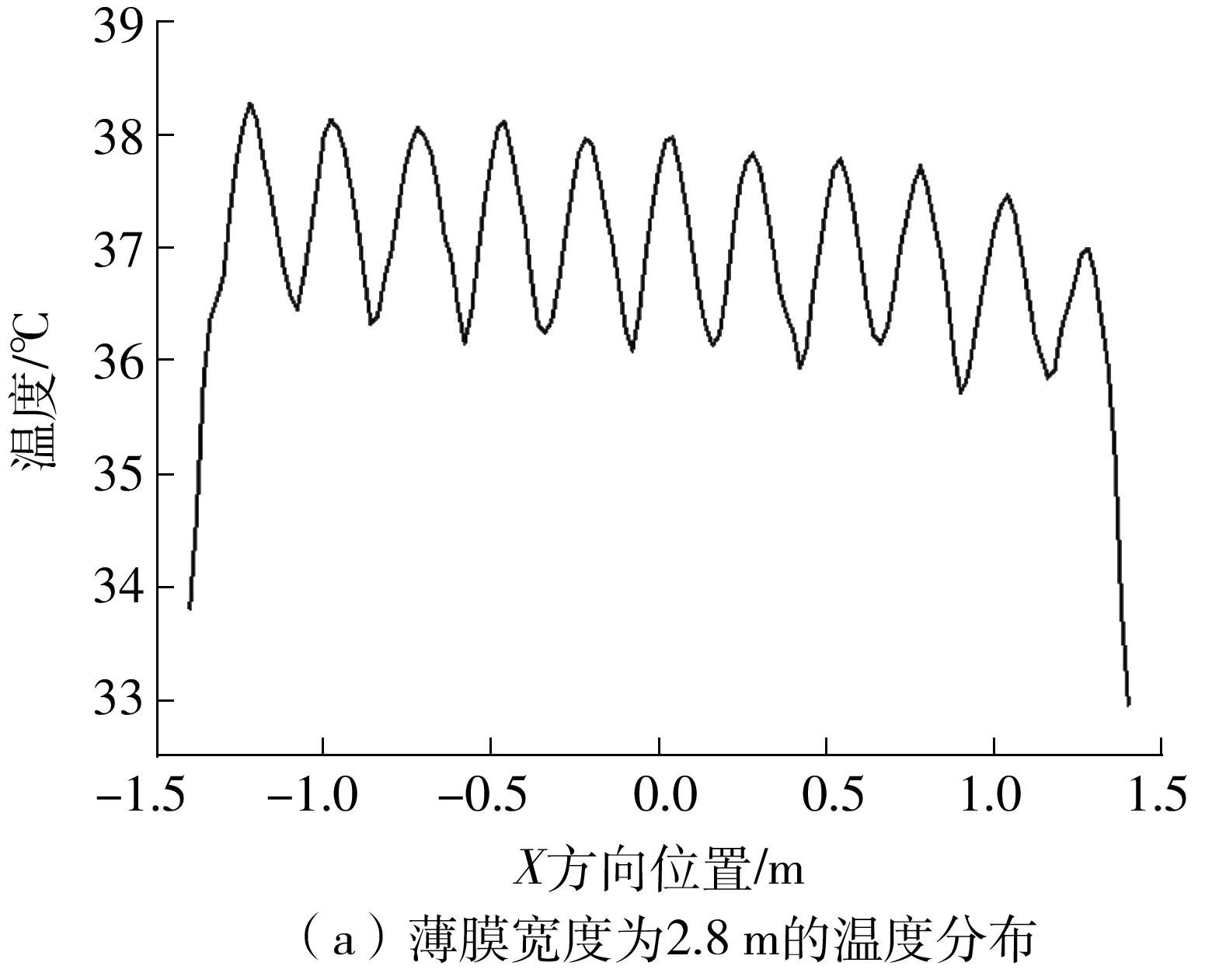
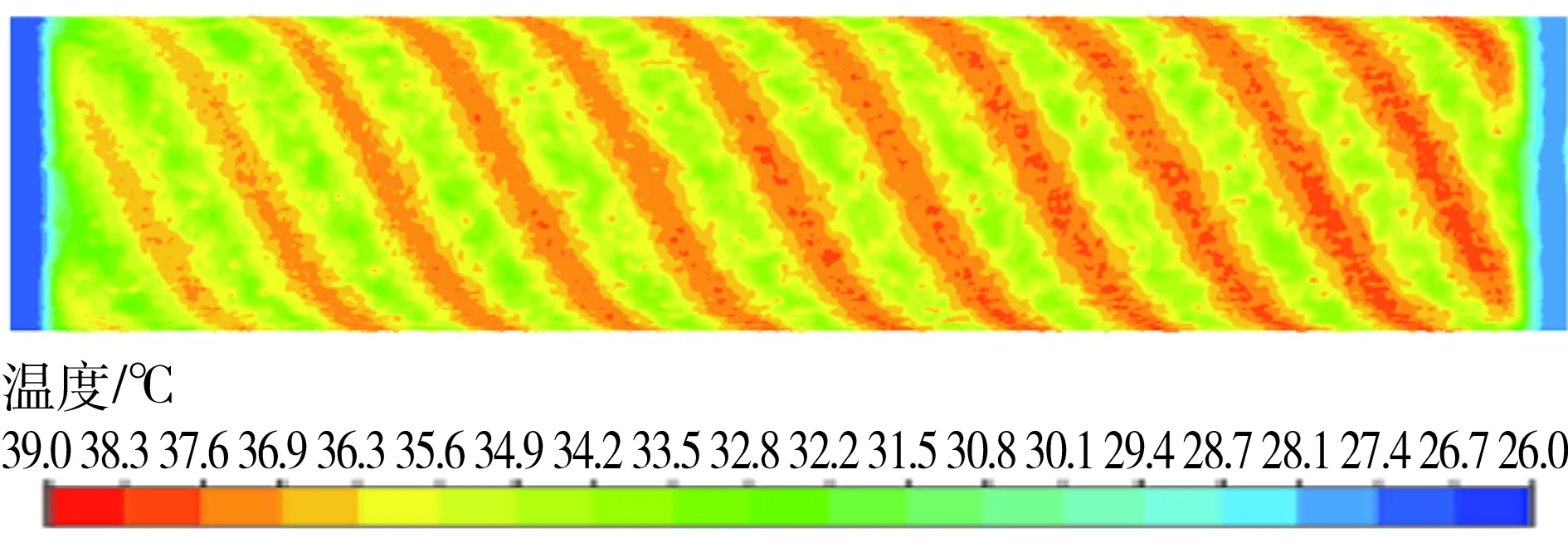
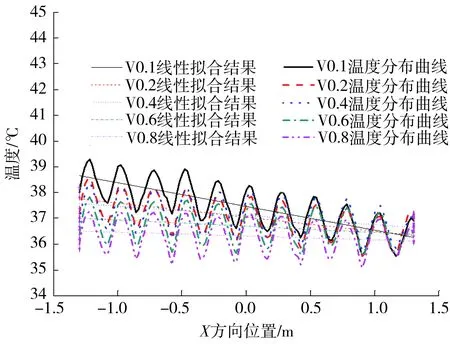
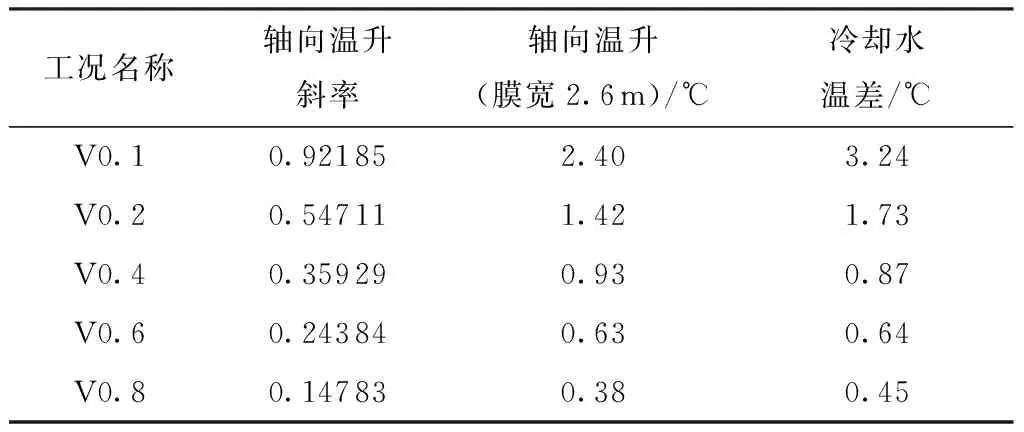
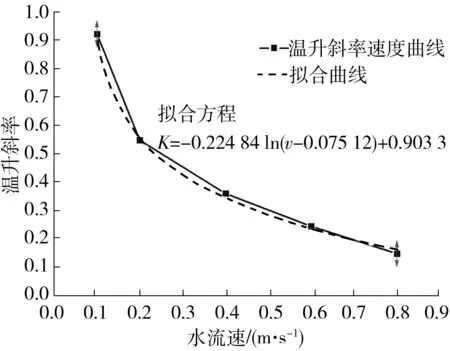
由表2可知mesh 1-mesh 3的质量流量逐渐减小,而mesh 4质量流量增加,随后mesh 5又开始降低,由此可知网格数量从mesh 3逐渐增大以后,质量流量仿真结果开上下始波动。本研究最后选用mesh 4对应的网格进行数值模拟。对于k-ε湍流模型,近壁区的处理一般采用壁面函数法或低Re数k-ε模型。根据文献[25]介绍,近壁区30 文中采用有限体积法对控制方程组进行离散,流动模型选用标准k-ε模型,添加能量方程,压力-速度耦合模型采用SIMPLE算法,湍动能及湍流耗散率采用一阶迎风格式,动量方程和能量方程采用二阶迎风格式。收敛标准方面要求能量方程残差小于e-6,其它计算变量残差小于e-3,此外监测冷却水出口流量及平均温度需要平稳。计算采用瞬态模拟,计算总时长10 min,前8 min时间步长为0.01s,后2 min更改时间步长为0.001 s。 流延薄膜传热过程仿真参数主要有边界条件、物性参数。 2.1.1 主要边界条件 薄膜、辊筒与周围空气的对流换热系数,设定为常数5 W/(m2·K),考虑到周围空气靠近模头处空气温度高,远离模头处空气温度低,因此设置周围空气温度为与模头距离有关的函数,如式(5)所示,表明在模头位置处空气温度大约为130 ℃,在远离模头最远处空气温度大约35 ℃。 (5) 辊筒外表面线速度为180 m/min。 冷却水流量42 m3/h,冷却水进口温度26 ℃,冷却水出口为压力出口,出口背压0.1 MPa,回流温度28 ℃。 薄膜从模唇流出温度220 ℃,即薄膜入口温度为220 ℃,薄膜厚度20 μm,薄膜流速与辊筒线速度相等即3 m/s。 冷却水与流延辊内侧相交处、流延辊外侧与薄膜相交处采用耦合交界处理。 2.1.2 有关的仿真物性参数 有关的仿真物性参数见表3所示。 表3 仿真有关物性参数Table 3 Physical parameters related to simulation 2.2.1 薄膜温度云图分布 仿真过程中对其残差曲线进行监控,残差曲线如图4所示。由图4可见,此时能量方程残差曲线已小于e-6,其它计算变量残差小于e-3,可认为计算达到收敛。此外,还对冷却水出口平均流速、冷却水出口平均温度进行监控,冷却水出口参数曲线如图5所示。由图5可知,在480~600 s(8~10 min)内,出口冷却水平均流速监控曲线平稳,其值大小基本不变;冷却水水温变化约为0.1 ℃,变化已经很小,可以认为计算到10 min以后整个系统达到平稳。 图4 仿真过程中的残差曲线截图Fig.4 Residual report during the simulation 图5 冷却水出口参数曲线Fig.5 Monitoring parameters curve of cooling water out 选取600 s时的结果进行分析,可知高温的流延膜经模头挤出以后,流延到流延辊表面,随着辊筒旋转的同时被辊筒内部冷却水迅速冷却。辊筒表面的薄膜温度分布云图如图6所示。由图6可知,在云图上方位置处,薄膜刚从模头挤出后流延到辊筒表面,其温度较高,随后跟着辊筒一起旋转,温度被辊筒内部冷却水迅速冷却而温度急剧降低。此外,由于流延辊冷却水流道采用了螺旋导流片,焊有导流片位置处没有冷却水的流动,导流片位置处换热量较小,表现为薄膜温度分布整体呈现“流道痕”现象,这与现场实际测试结果相吻合。图7所示为采用瑞典FLIT红外热像仪对流延膜温度分布的测试结果。FLIT热像仪型号为E40,设备像素160×120,热灵敏度<0.07 ℃,测温范围-20~+650 ℃,精度为±2 ℃或读数的±2%。 图6 流延膜温度云图分布Fig.6 Temperature distribution of casting film 图7 红外热像仪测试温度分布Fig.7 Temperature distribution measured by thermal imager 2.2.2 薄膜周线温度变化分析 图8 周线选取示意图Fig.8 Schematic diagram of perimeter line 由图9可知,薄膜温度主要分两个阶段:温度骤冷阶段和温度平稳阶段。在骤冷阶段(薄膜在辊筒上移动距离约0.1 m,停留时间在0.03 s以内),薄膜温度迅速冷却,温度从220 ℃迅速冷却到40 ℃以内;在温度平稳阶段,即停留时间大于0.03 s以后,薄膜温度趋于平稳,温度波动很小。此外,从图9还可以看出,薄膜内外表面温度分布大小基本一致,在温度骤冷阶段内外温差稍微较大(<5 ℃),在温度平稳阶段,薄膜内外温度几乎无变化。图10(a)为吴哲浩等[22]对薄膜宽度中心线上轴向温度的研究结果,由图示结果可知,该研究中薄膜厚度最小值为0.1 mm,薄膜冷却过程没有明显的骤冷阶段。图10(b)为李晓伟等[20]的研究中涉及到的一个旋转周期内薄膜和流延辊外壁面温度变化情况,该薄膜厚度为30 μm,采用Matlab编程计算,认为塑料薄膜的主要冷却过程发生在前0.5 s。 图9 薄膜温度沿周线长度及随停留时间的分布Fig.9 Temperature distribution of perimeter length/residence time 图10 已有文献中的相关研究结果Fig.10 Relevant research results in the existing literature 2.2.3 薄膜轴线方向温度分布 在距离薄膜入口约0.47 m,即薄膜转动角度90°处,沿X轴线方向在膜面表面选取一条直线,如图11所示(该位置处薄膜已经处于温度平稳阶段),考察薄膜温度沿轴线方向(即薄膜宽度方向)的分布。薄膜轴线方向温度分布如图12(a)、12(b)所示,图中横坐标为轴线方向。由图12(a)、12(b)可知,薄膜未切边时,即膜宽为2.8 m,薄膜两端分别有一小段的低温区,其余位置为温度波动的高温区,两端的最低温度比中部的高温区低了约有3 ℃,中部高温区温度上下波动,波动幅度在±1 ℃以内。图12(c)为吴哲浩等[22]对薄膜宽度方向温度分布情况的研究结果,由于为平行流道,薄膜温度未有上下波动情况。 图11 轴线选取示意图Fig.11 Schematic diagram of axis selection 图12 文中以及已有文献中薄膜沿轴线方向的温度分布Fig.12 Axial temperature distribution in this paper and in the existing literature 工程实际生产过程中,薄膜一般会对两边的低温区域进行切边处理,切边宽度一般大于10 cm,切边后的温度分布如图12(b)所示,此时薄膜宽度为2.6 m。对切边后的薄膜温度曲线进行线性拟合,拟合曲线方程斜率为-0.328 27,即薄膜进口端到出口端平均温升斜率为0.328 27,则可计算切边后的薄膜轴线平均温升为2.6×0.328 27≈0.85 ℃。 2.2.4 流延辊表面温度分布 图13为流延辊筒表面温度分布云图,由图可知,辊筒表面与薄膜接触处温度较高,辊筒两端由于没有与薄膜接触,因此两端各自留下一条狭窄的低温带。在与薄膜接触的区域,由于辊筒内的流道是螺旋型流道,导流片位置对应于辊筒表面呈现出一条条螺旋高温带,可见辊筒表面温度不均匀,有螺旋导流片处辊筒表面的温度高,各螺旋导流片之间辊筒表面温度低。 图13 流延辊筒表面温度分布Fig.13 Surface temperature distribution of the casting roller 2.2.5 冷却水流道温度分布 服务器系统软件采用Windows 2000 Professional作为网络服务器,它有良好的安全措施与先进的兼容能力,内置Internet/Intranet功能,实用的管理导向,同时支持TCP/IP协议,并有较高运行速度,系统发布则Microsoft的Internet信息服务(Internet Information Server 5.0,即IIS)。IIS是Windows组件,此组件可以很容易将信息和应用程序发布到Web。而使各个用户端则采用Windows XP、7操作系统,IE9.0以上的浏览器。 图14为流延辊筒内部冷却水温度分布,其中冷却水从左侧向右侧流动,冷却水流入螺旋流道以后,高温流延膜的热量通过辊筒传递给冷却水,使冷却水温度增高,整体上左侧流入段水温较低,右侧流出端水温较高,辊筒左右两侧水管的温差为0.8 ℃。 图14 冷却水温度分布Fig.14 Temperature distribution of cooling water 为了考察冷却水流速对薄膜冷却的影响,本研究选取流延辊螺旋流道内不同冷却水流速下的情况进行对比仿真分析,仿真时长600 s,仿真主要参数如表4所示。图15分别为中部螺旋流道内不同冷却水流速下薄膜及辊筒表面温度分布云图,由图可知,在大流速情况下,辊筒表面及薄膜温度较低,表明增大流量有助于薄膜的冷却。 图15 不同冷却水流速下薄膜及滚筒表面的温度分布Fig.15 Surface temperature distribution of casting film and casting roller under different cooling water flow velocities 表4 仿真有关物性参数Table 4 Physical parameters related to simulation 图16为不同工况下,薄膜中部位置处周线温度的分布情况。由图可知,不同流速下,薄膜温度骤冷阶段与温度平稳阶段分布趋势一致,在温度骤冷阶段,不同流速对薄膜的冷却效果几乎无差别,在温度平稳阶段,流速对薄膜温度的影响也较小,流速大时薄膜温度低,流速小时薄膜温度高,流速从0.1 m/s增加到0.8 m/s时,薄膜在平稳阶段的温度降低约1 ℃。 图16 不同工况下薄膜周线温度分布Fig.16 Film temperature distribution along the circumference length in different working conditions 图17为不同工况下切边后薄膜宽度为2.6 m时轴向温度分布曲线。由图可知,不同工况下,薄膜轴向温度均上下波动,波动幅度在±1 ℃范围内。对不同工况下温度曲线进行线性拟合(V0.1、V0.2、V0.4、V0.6、V0.8对应的拟合方程分别为 图17 不同工况下薄膜轴线温度分布Fig.17 Film temperature distribution in axial direction in different working conditions y=0.921 85x+37.472 59、y=0.547 11x+37.057 6、y=0.359 29x+37.124 37、y=0.243 84x+36.710 04、y=0.147 83x+36.330 41),发现薄膜从进口端到出口端温度逐渐升高,流量越低,薄膜温升越大。表5为不同流速条件下有关仿真结果对比,可见流速越低,薄膜轴向温升曲线斜率越大,冷却水出口温度越高,冷却水流速对薄膜轴向方向影响较大。 表5 不同流速下仿真结果Table 5 Simulation results in different velocities 图18为不同平均流速条件下薄膜厚度为20 μm时轴向温升斜率情况,可根据薄膜温升斜率对流延薄膜流量设计提供技术指导。如薄膜切边后宽度为D,流延辊冷却水水道内外径分别为r1、r2,流延辊螺旋导流条个数为n,螺旋角度为θ。现假定宽度为D的薄膜要求轴向温升小于W(℃),则流量可进行如下评估设计。 1)根据要求,轴向温升 2)根据斜率K,从图18中查询斜率为K时螺旋流道内冷却水流速v,为了便于查询,将斜率与水流速度进行对数拟合,拟合方程为: 图18 不同流速薄膜轴线温升斜率Fig.18 Temperature rise slope along the axis under different flow velocity K=0.090 33-0.224 84ln(v-0.075 12) (6) 3)根据流速v,可进行流量Q计算, Q=A·B·sinθ·v·n (7) 将式(7)进行整理后为 (8) 针对流延薄膜传热过程中,薄膜厚度很薄,直接进行传热模拟时网格数量巨大、无法有效模拟冷却过程的问题,提出了将薄膜进行加厚的薄膜传热仿真模型,最后顺利实现对薄膜传热过程的模拟,有关的仿真结论如下。 (1)文中提出的用于模拟流延薄膜的传热模型,对薄膜进行增厚处理,极大降低模型网格数量,加快数值计算速度,实现了流延薄膜冷却过程的仿真模拟,得到了薄膜温度分布云图,轴向温升大小等信息,与现场实际测验结果相符。 (2)由于流延辊内部焊有螺旋导流片,导致辊筒表面与薄膜温度场出现螺旋型分布,呈现“流道痕”现象,在有螺旋导流片位置处薄膜及辊筒表面温度高,冷却水流道对应位置温度低;薄膜轴向方向上薄膜温度上下波动,温度波动幅度在±1 ℃以内,且从冷却水进口端到出口端,薄膜温度波动上升。 (3)薄膜在流延辊上冷却主要分为两个阶段,即温度骤冷阶段和温度平稳阶段,薄膜的冷却主要发生在骤冷阶段;薄膜在辊筒表面停留时间在0.03 s内、移动距离约0.1 m,温度从220 ℃迅速冷却到40 ℃以内;在温度平稳阶段,薄膜温度趋于稳定,波动很小;薄膜厚度方向的温差在骤冷阶段稍大(<5 ℃),在平稳阶段厚度方向几乎无温差。 (4)提高螺旋流道内冷却水平均流速时,薄膜在周线方向的温度变化较小,流速从0.1 m/s增加到0.8 m/s时,薄膜温度平稳阶段的温度降低仅约1 ℃;在轴线方向,薄膜平均温升斜率受流速影响较大,流速从0.1 m/s增加到0.8 m/s时,轴向温升斜率从约0.15增大到约0.92,对于切边后宽度为2.6 m的薄膜,轴向温升从0.38 ℃增加到2.40 ℃。 (5)文中给出了薄膜厚度20 μm时流延辊螺旋流道水道平均流速与薄膜轴向温升斜率关系,据此可对流延辊流量设计提供技术参考。1.5 仿真计算方法
2 流延薄膜传热特性仿真
2.1 仿真参数
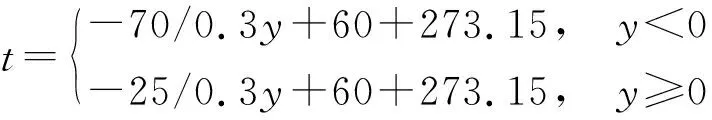

2.2 仿真结果


3 不同流速下的仿真分析
3.1 不同流速下的温度云图分布

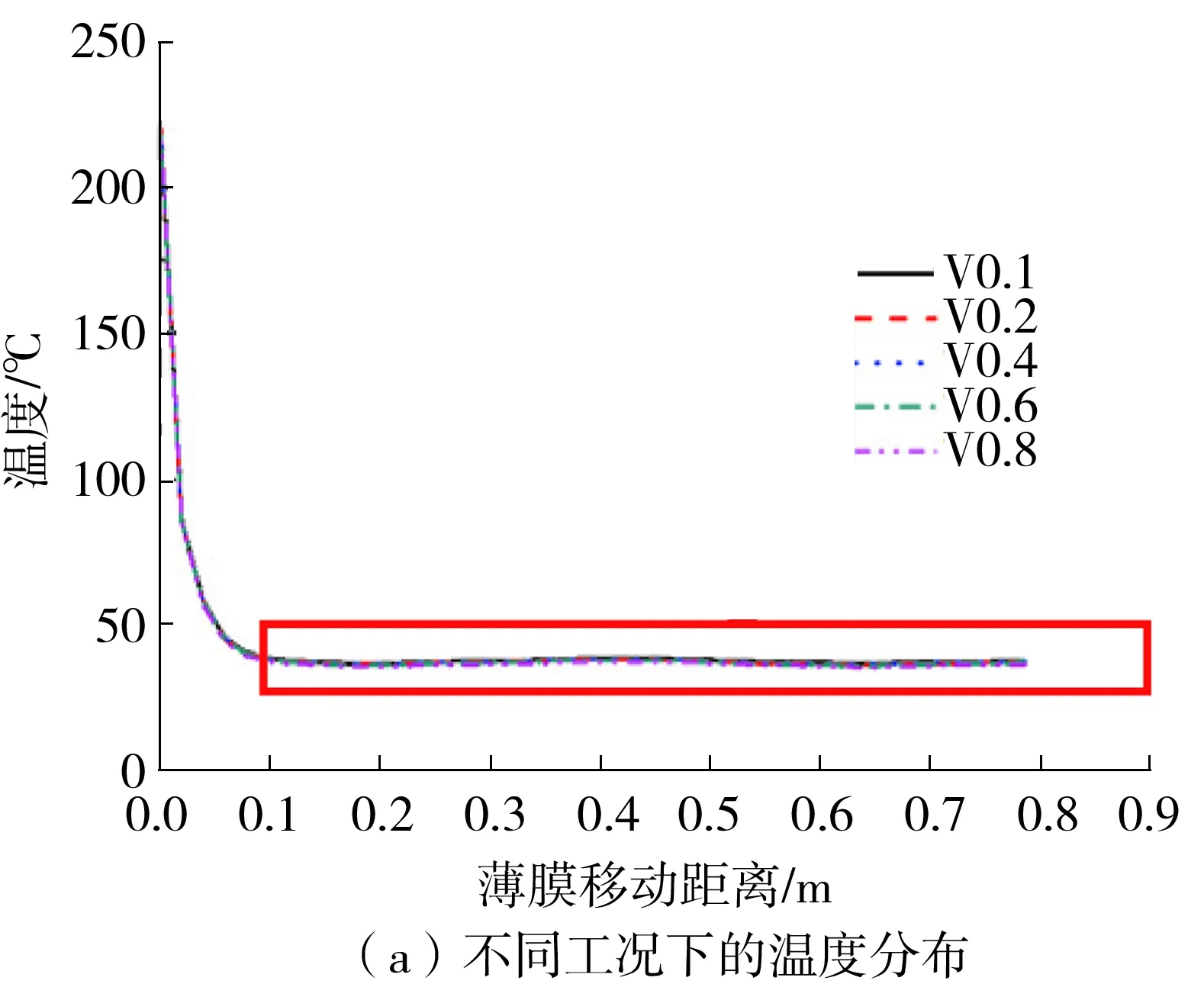
3.2 不同工况下薄膜周线的温度变化
3.3 不同工况下薄膜轴线方向温度分布
4 流延辊筒流量设计方案


5 结论
