液晶光波导中本征模内场分量间的关系

查正桃，张谦述

(1.西华师范大学 物理与天文学院，四川 南充 637009;2.西华师范大学 电子信息工程学院，四川 南充 637009)

1 引 言

向列相液晶的大双折射[1]和易被低电压调节[2]特性，有助于改善光波导的光学性能。因此，近年来向列相液晶光波导的研究引起了国内外研究人员的兴趣。例如，向列相液晶光波导在光开关[3-5]、光衰减器[6]、光学滤波器[7]、可调光分束器[8]、偏振旋转器[9-10]等器件中的应用研究被广泛开展。

在以上研究中，液晶光波导的模场分析是最基本、最重要的步骤。自20世纪80年代以来，大量数值方法被相继提出，主要包括变分法[11-12]、有限差分法[13]、矢量伪谱法[14]、有限元法[15-16]等，但这些数值方法仅适用于均匀各向异性光波导。然而，一般情况下液晶光波导都具有锚定层，根据Freedericksz转变[17]，当外加电压使液晶分子指向矢旋转时，其旋转角是沿外加电场方向渐变的，因此并不能通过上述数值方法分析液晶光波导的模场分布。至今，横向各向异性液晶光波导中的场分量间关系仍不清晰。此外，参考文献[14]推测出液晶光波导中本征模场的模内场分量间存在相关性，但并未给出相应的定量关系。因此，为了得到液晶光波导中的模内场分量间的定量关系，本文首先从麦克斯韦方程组推导出向列相液晶的各向异性电磁场耦合方程，并得出非寻常光本征模式的场分量间比值与指向矢旋转角间的定量变化规律。考虑到液晶指向矢旋转角由外加电压确定，因此，可进一步得出本征模内场分量之间的振幅、相位的定量关系受外加电压调控的规律，并使用光学软件OptiBPM13.1进行数值仿真验证。

2 模内场分量间关系的理论分析

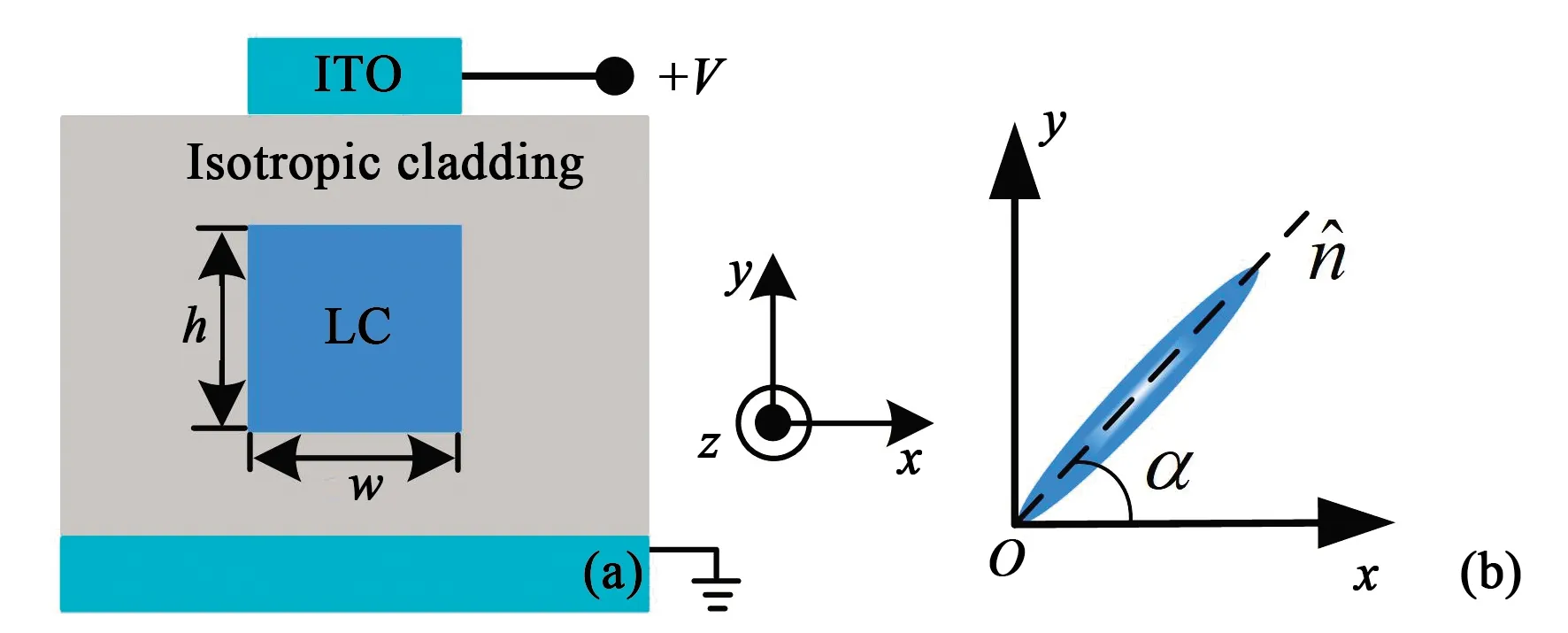
图1 (a)液晶光波导横截面示意图；(b)液晶分子旋转示意图。

(1)

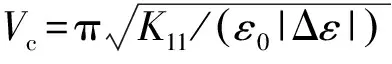
(2)

式中，

(3)

其中：ε‖、ε⊥分别表示光学频率下平行和垂直液晶分子长轴的相对介电常数。联合式(1)～(3)即可得到任意外加电压下的液晶介电张量分布。

另一方面，根据麦克斯韦方程组，非磁各向异性电介质的磁场矢量波动方程为[21]

(4)

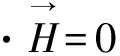
(5)

(6)

将式(6)乘tanα(y)后与式(5)相加并整理可得：

(7)

根据本征模场理论[22]可将式(7)改写为：

(8)

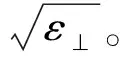
(9)

成立。将式(9)代入式(8)可得:

Hxe=-tanα(y)Hye，

(10)

式(10)表明在液晶光波导的芯区，非寻常光波所激励的本征模场的横向磁场分量之间存在如下关系：

(1)模场振幅的比值为当前液晶分子旋转角的正切函数；

(2)当液晶分子旋转角的正切函数不恒等于零时，模场之间的相位差恒为π。

而根据式(1)可知，液晶分子旋转角由外加电压确定，因此，非寻常光波本征模式的横向磁场分量的场间关系可被外加电压定量调控。

3 仿真实验

以液晶5CB(4′-n-pentyl-4-cyano-biphenyl)为例，真空波长λ0设为1.5 μm，在室温25.1 ℃下5CB为单轴、正性液晶，其Frank弹性常数K11、K33分别为6.4 pN、10 pN[17]，根据双系数柯西模型[17]可知，液晶分子的主轴介电常数为ε‖=2.829 1,ε⊥=2.309 2，包层折射率选择nc=1.48，液晶芯区的尺寸w、h均为6 μm。根据式(1)可得不同外加电压下液晶分子旋转角渐变曲线如图2所示。

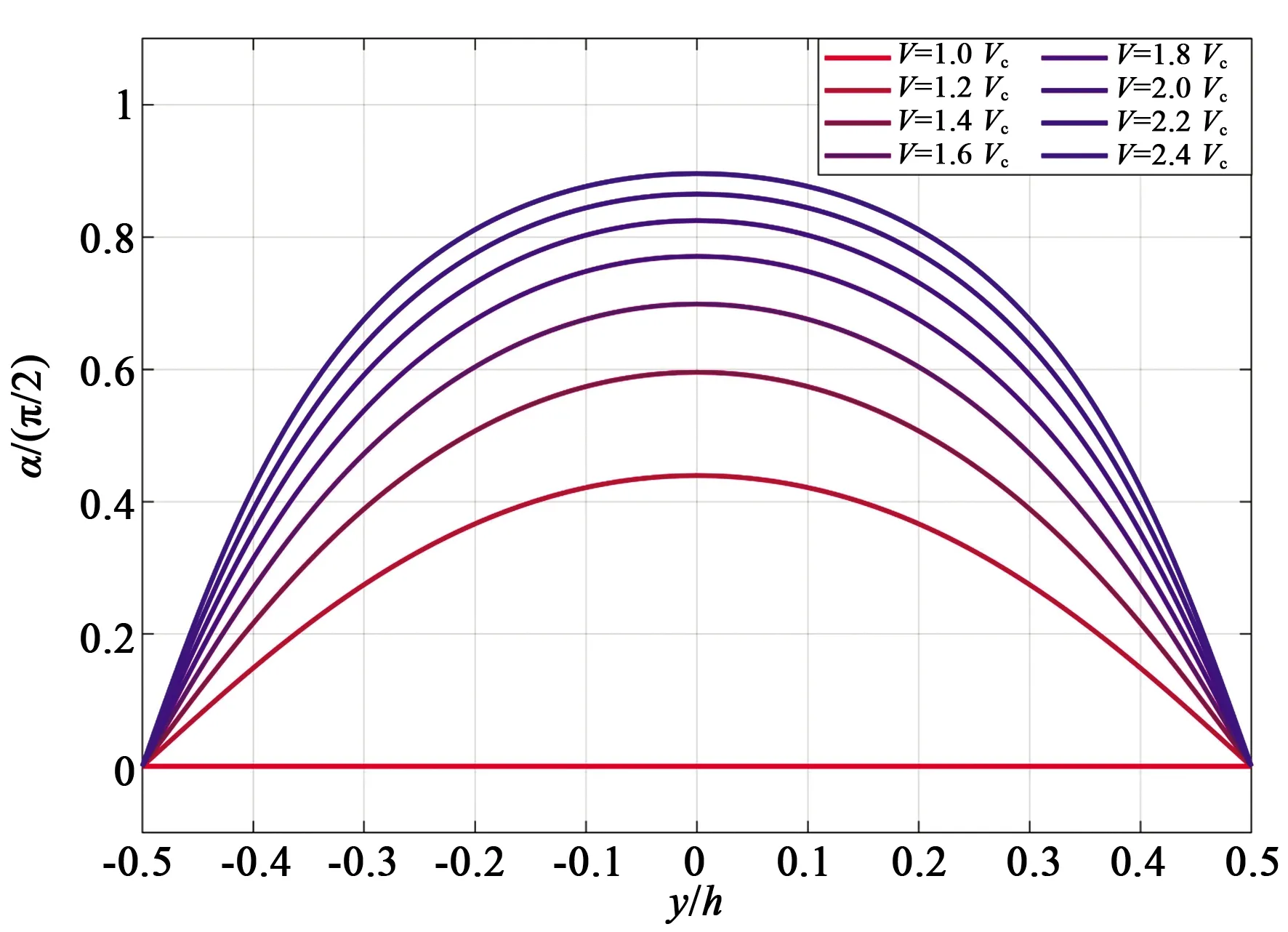
图2 液晶分子旋转角在不同外加电压下的分布曲线

从图2可见，当外加电压超过阈值以后，液晶分子指向矢的旋转在y方向是渐变的，为了能够使用软件OptiBPM13.1中适用于均匀各向异性光波导的算法进行求解，将渐变的液晶芯区用多层均匀的液晶层近似代替，等效模型如图3所示。

图3中，第i层均匀液晶层的位置yi由式(11)确定。

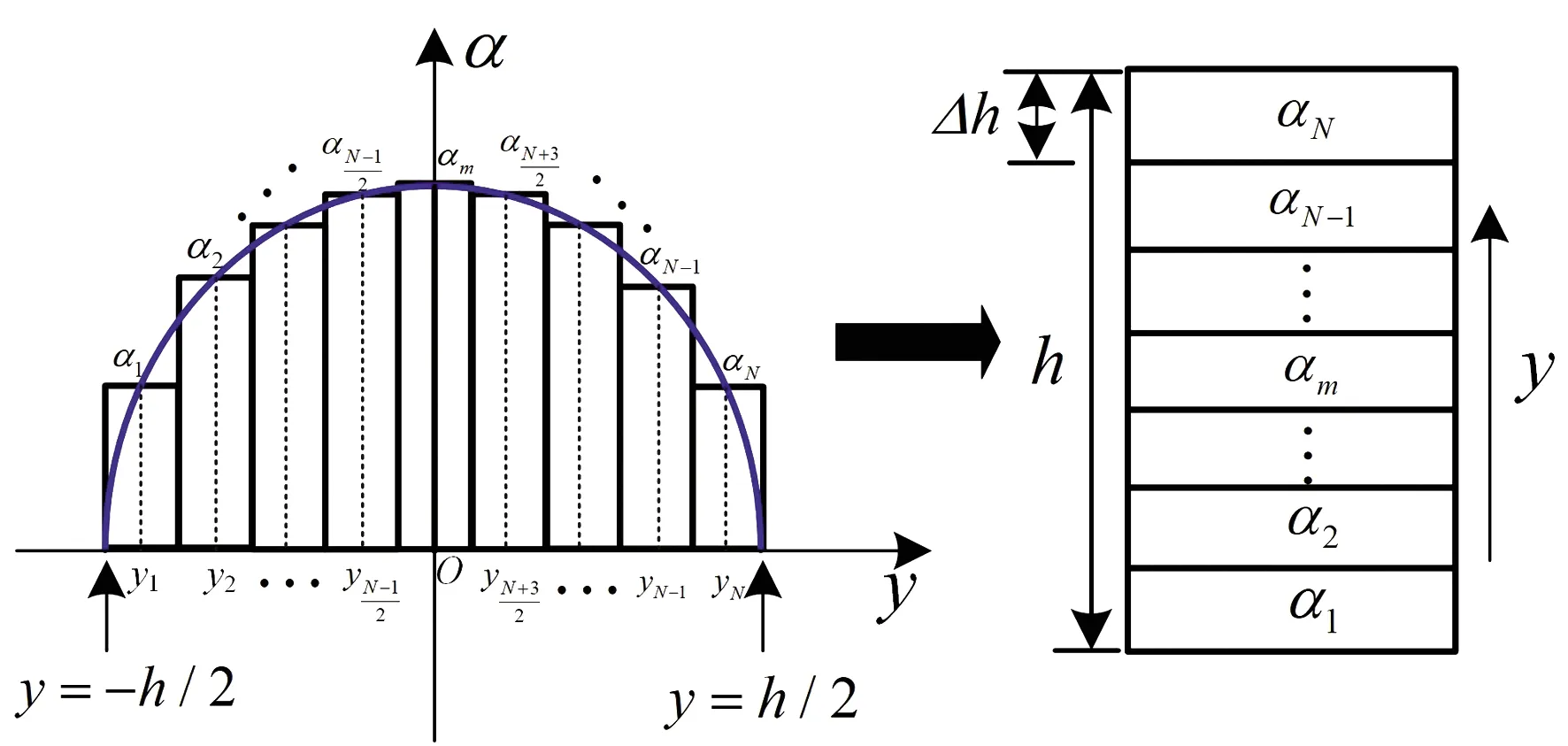
图3 液晶芯区的多层近似模型示意图

yi=-h/2+(2i-1)Δh/2,i=1,2,…N，

(11)

式中，Δh=h/N为每一层的厚度，N为层数。考虑到对称性，N应为奇数。显然，N取值越大，这种等效模型的准确度越高。只要液晶芯区的厚度和层数确定，即可通过式(11)和上述各式得到每一层液晶分子的介电张量。这里选择液晶层数N=301，计算窗口为9 μm的正方形区域。当外加电压分别为阈值电压的1.2倍和2倍时，波导横截面的介电张量分布如图4所示。

从图4(a)～(c)和图4(e)～(g)可见，液晶介电张量在y方向是渐变的，但在x方向却是均匀的。对于正性液晶，非寻常光所激励的本征模式为低阶模式，利用OptiBPM13.1软件求解这两个外加电压下液晶光波导中的本征模场，图5和图6展示了外加电压分别为阈值电压的1.2倍和2倍时，非寻常光波所激励的前4个模式的Hx,tanα(y)Hy的振幅以及横向磁场分量的相位在液晶光波导芯区的分布情况。

图4 (a)～(d)外加电压为1.2倍阈值时液晶介电张量的横截面分布；(e)～(h)外加电压为2倍阈值时液晶介电张量的横截面分布。

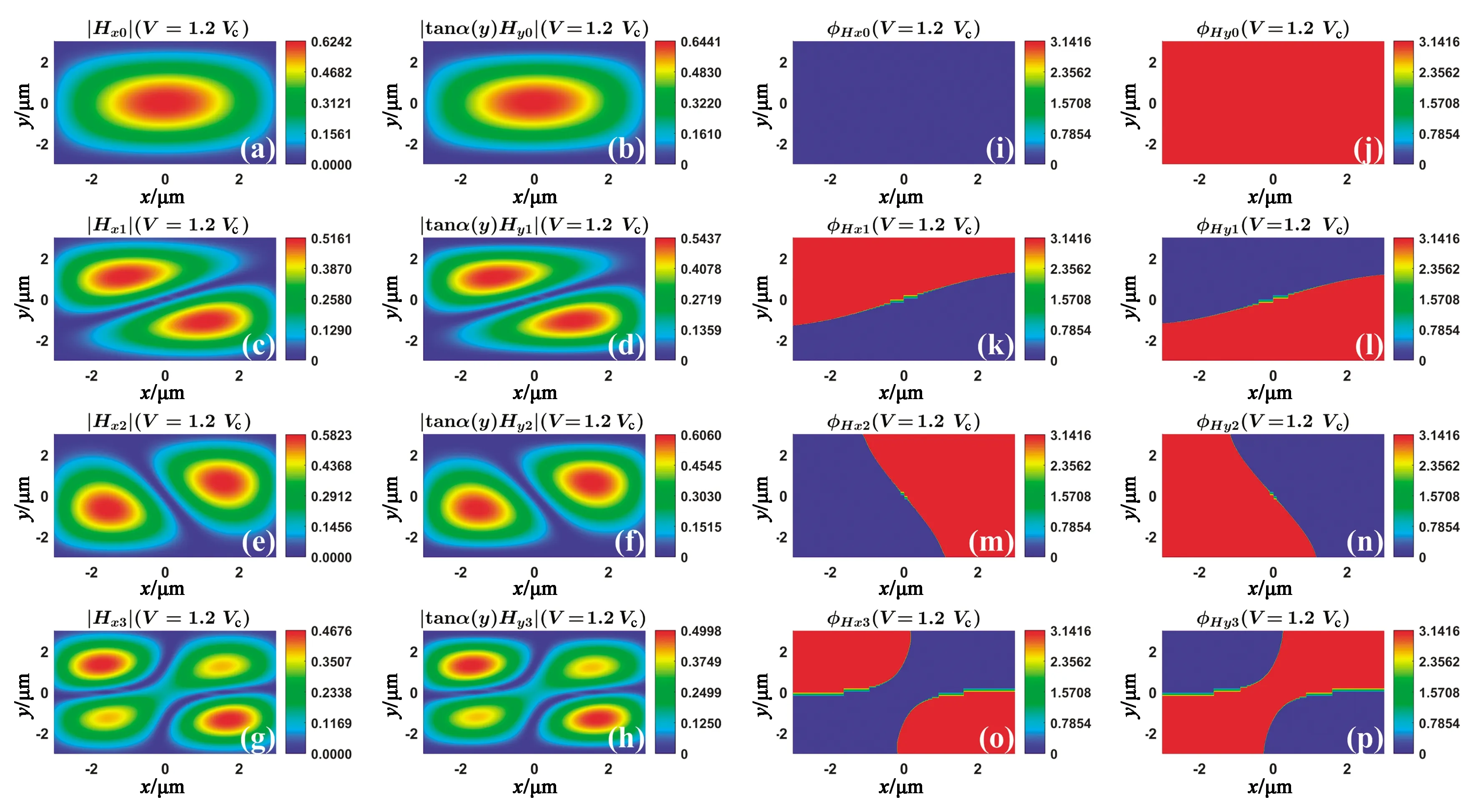
图5 外加电压为1.2倍阈值时，前4个模式横向磁场分量在液晶光波导芯区的分布情况。(a)～(h)振幅分布；(i)～(p)相位分布。

图6 外加电压为2倍阈值时，前4个模式横向磁场分量在液晶光波导芯区的分布情况。(a)～(h)振幅分布；(i)～(p)相位分布。

从图5(a)～(h)和图6(a)～(h)可以看到，对于非寻常光波所激励本征模场，|Hx|与|tanα(y)Hy|的图案形状几乎是完全相同的，而且根据彩色条注的数值可以看到它们的数值也非常接近，考虑到数值算法以及液晶芯的多层划分存在一定的误差，因此二者并不是完美地相等。而且从图5(i)～(p)和图6(i)～(p)可见，各阶模式的横向磁场分量在整个波导芯区上的任意一个位置上相位差几乎都为π。因此，式(10)所表征的横向磁场分量场间关系受液晶分子旋转角(或外加电压)调控的定量关系式是成立的。应当指出的是，尽管这里仅展示了前4个模式，但根据仿真实验结果发现，非寻常光波所激励的更高阶模仍然满足该规律。通过改变波导的宽厚比、入射波长以及材料的折射率等参数进行多次仿真实验，发现非寻常光波激励的本征模场的模内横向磁场分量之间仍然满足式(10)。

此外，将图5(a),(c),(e),(g)和图6中与之对应的子图进行比较还可以看到当外加电压更大时，Hx的振幅也更大。这是因为随着外加电压增加，液晶分子的旋转角也增加(图2)，根据式(10)可知Hx相对于Hy的振幅也随之增加。当外加电压非常接近于阈值电压或者更小的情况，Hx相对于Hy的振幅非常小，此时非寻常光波所激励的本征模非常接近准横电(Transverse Electric, TE)模；随着外加电压的增加，Hx相对于Hy的振幅逐渐增加，非寻常光波所激励的本征模式逐渐接近于准横磁(Transverse Magnetic, TM)模。因此，可以通过改变外加电压来实现非寻常光波所激励的偏振模式的转换，即根据式(10)所示的调控规律能够实现基于液晶光波导的电控偏振旋转器以及模式转换器。

从式(10)还可以看到当外加电压超过阈值以后，非寻常光波所激励的横向磁场分量之间的比值不仅与当前外加电压有关，而且该比值与空间变量y也有关系，这将导致横向磁场分量在y方向上的模场直径并不相等。这一现象与文献[14]中横向磁场分量间模场直径相等的结论有所不同，这是因为文献[14]中是假设所有液晶分子的场致重新取向是一致的，即并未考虑液晶指向矢的旋转是一维渐变的(本文中渐变方向为y方向)。

总之，在外加电压下，液晶指向矢的渐变旋转对液晶光波导的模场分布有较大的影响，适用于常规均匀各向异性光波导的数值算法并不能直接有效地分析液晶光波导中的模场分布和场间关系。

4 结 论

针对横向各向异性液晶光波导中模内场间关系并不清晰以及传统数值算法并不能直接分析具有锚定层的液晶光波导模场的情况，本文从解析上根据麦克斯韦方程组推导出液晶各向异性磁场耦合本征方程，并得出非寻常光的本征模场分量间关系受外加电压调控的定量关系式,并使用光学软件OptiBPM13.1进行仿真验证。结果表明，本文得出的可通过改变外加电压来定量调控液晶光波导中非寻常光波激励的偏振模式的物理规律是有效的，这一规律有助于推动基于液晶光波导的偏振旋转器和模式转换器的研究。