随机开放量子系统的纯态开关反馈控制

董智翔,丛 爽

（中国科学技术大学自动化系,安徽合肥 230027）

1 引言

根据系统是否与环境有相互作用,量子系统可分为封闭量子系统和开放量子系统,封闭量子系统是一个孤立的、与外界没有相互作用或能量交换的系统,这类系统的状态演化是确定的.在实际的量子信息处理和量子计算中,系统往往由于自身或外界情况的不同而成为开放量子系统[1].在量子领域的各类研究中,量子系统的状态转移对量子化学和原子物理学等应用具有重要意义[2—3],为了控制量子系统状态转移至目标态,许多经典的控制策略已经应用于量子系统,例如:最优控制[4]、滑模控制[5]、H∞控制[6]及李雅普诺夫控制[7—8]等,其中,量子系统的反馈控制可以获得更高的控制精度.然而,当反馈控制技术应用于量子系统时,需要考虑测量对量子系统的影响,而量子系统的测量将导致系统状态不可避免地以一种概率的方式发生变化[9].考虑到量子系统测量的特殊性,Belavkin等人将连续测量和反馈控制相结合,提出了基于量子系统测量的反馈控制,系统信息可以通过量子滤波器获得[10].连续测量的量子滤波器的数学模型是一个随机微分方程,称为随机主方程（stochastic master equation,SME）.基于SME,van Handel等人研究了二维随机量子系统本征态的反馈控制[11].针对角动量系统,Mirrahimi等人提出了一种开关反馈控制律,首次实现了量子系统状态从任意初始态到任意本征态的全局稳定的状态转移[12];Tsumura在Mirrahimi所提出控制律的基础上提出一类连续控制律实现任意初始态到某个本征态的转移[13].为了将受控量子系统扩展到更一般的有限维随机量子系统,Ge等人设计了一种非光滑状态反馈控制,实现了本征态的状态转移[2].对于随机开放量子系统的状态转移,系统除有限个目标态以外,往往还存在着多个平衡点,如何控制系统状态收敛到目标态而不是其他平衡点是难点之一,为此,利用李雅普诺夫稳定性定理和拉塞尔不变集原理,Cong等人实现了随机开放量子系统一类特殊本征态和任意本征态的状态转移[14—15];Wen等人实现了一类具有简并测量算子的有限维随机量子系统的混合态的全局稳定和状态转移[16].到目前为止,还没有随机开放量子系统叠加态开关控制研究成果的相关报道.

本文通过开关控制律的设计,实现对随机开放量子系统状态的状态转移和收敛控制,目标态为同时包括本征态和叠加态的纯态,通过设计控制律,使得系统状态可以从状态空间的任意初态收敛到目标态.为此,设计的控制律包含两部分,一是常量控制,用于将系统状态从收敛域之外驱动到收敛域;二是基于李雅普诺夫稳定性定理和拉塞尔不变集原理设计的控制律,使通过第一步控制进入到系统收敛域中的系统状态收敛到目标状态.当目标态为本征态时,该状态是任意选取的.当目标态为叠加态时,对于单比特量子系统,该状态也是任意选取的;对于2比特或多比特量子系统,该状态需要通过单量子位张量积的形式获得,这是为了保证系统的平衡点是可数个.在系统数值仿真实验中,笔者将所设计的控制律与文献[15]中设计的控制律应用于2比特量子系统的状态转移中,目标态分别为本征态和叠加态,并将对状态转移的结果进行性能对比和分析.

本文的结构安排如下:第2节为随机开放量子系统的数学模型及控制任务描述;第3节为李雅普诺夫方法设计的控制律和常量控制组成的开关控制律及其特性分析;第4节为基于上述开关控制律的系统数值仿真实验及其性能分析;最后第5节为全文总结.

2 被控系统及其任务描述

2.1 被控系统描述

有限维量子滤波器的状态可以用密度矩阵ρt表示,状态的演化为非线性随机微分方程,即随机主方程（SME）:

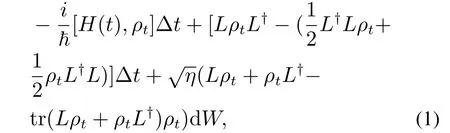
其中:量子状态密度矩阵ρt ∈S=:ρt=≽0,tr(ρt)=1},n为系统量子比特数,表示ρt的共轭转置,tr(ρt)表示ρt的迹,C表示复数集,S表示状态空间;ℏ为普朗克常量,通常设置为1;H(t)=H0+utH1为系统总哈密顿量,H0为自由哈密顿量,H1为控制哈密顿量,ut ∈R为外加控制,R代表实数集;L ∈为测量算符,确定系统和测量装置之间的相互作用;Δt为相互作用时间;η ∈(0,1]为测量效 率;令表示测量过程带来的确定性退相干作用,表现为Lindblad形式的漂移项;令表示测量过程带来的随机扩散项,表现为对量子系统状态产生的干扰.dW是零差测量时产生的随机噪声,满足E(dW)=0,E[(dW)2]=Δt的Wiener过程,E(·)表示随机变量的期望值.

2.2 控制任务和控制思路

对于一个n比特随机开放量子系统,本文所控制的目标态ρf为纯态,即本征态和叠加态.当目标态为本征态时,ρf是任意的;当目标态为叠加态时,ρf可由n个单比特叠加态ρf1的张量积计算为

其中:a(1-a)=bb*,b*表示b的共轭复数.

针对目标态为纯态的情况,本文设计一个开关反馈控制（switching feedback control,SFC）,来实现系统状态可以从状态空间的任意初态收敛到目标态.具体控制思路为首先,根据李雅普诺夫定理,构造一个合适的李雅普诺夫函数V,通过设计控制律u(ρt)使V的无穷小算子LV≤0,并且在目标态时V(ρf)=0,从而目标态是概率稳定的;然后,根据拉塞尔不变集原理,分析系统的不变集,并通过参数设置确定系统状态的收敛域,使得该收敛域中只包含目标态,则位于收敛域中的系统状态在控制律u(ρt)的作用下可以唯一地收敛到目标态.为了使不在收敛域中的系统状态也能收敛到目标态,设计了常量控制uc,在此控制律作用下,系统状态可以在有限时间内进入收敛域中.通过这样的方式,将控制律u(ρt)和常量控制uc组合成开关控制律ut,在ut的作用下,系统状态就可以从状态空间的任意初态收敛到目标态.

3 控制律设计及其特性分析

本小节中,首先基于李雅普诺夫稳定性定理设计控制律u(ρt);再基于拉塞尔不变集原理确定系统的收敛域,并给出参数取值的条件;最后给出开关控制律ut的具体表达式.

3.1 控制律u(ρt)的设计

构造一个李雅普诺夫函数:

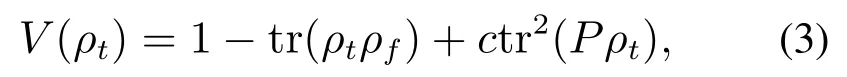
其中:c ∈R且c≥0,P ∈,满足tr显然V≥0且=0,满足李雅普诺夫函数设计要求.需要注意的是,在后面的工作中,通过设计（3）中的参数P和c,可以确定系统的收敛域,并使得收敛域中只包含目标态.

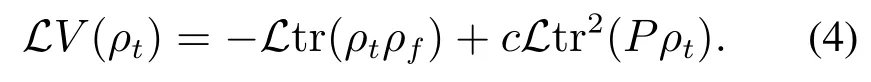
根据随机开放量子系统随机主方程（1）,有

因此,

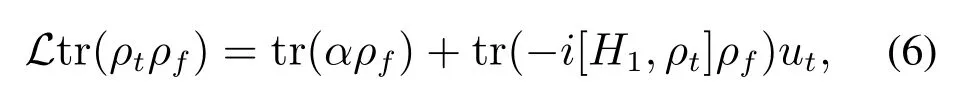
其中

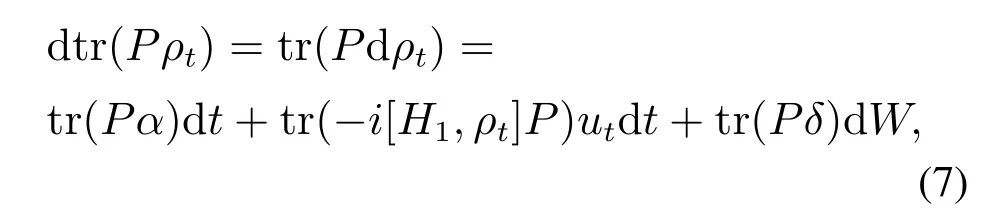
其中δ=利用伊藤引理（Ito lemma）[17],dtr2()可计算为

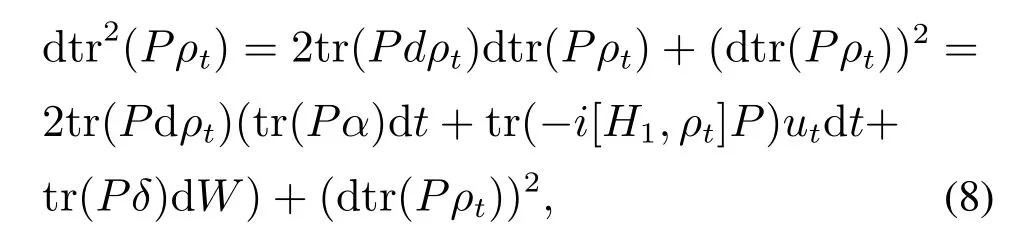
根据式（7）—（8）,有

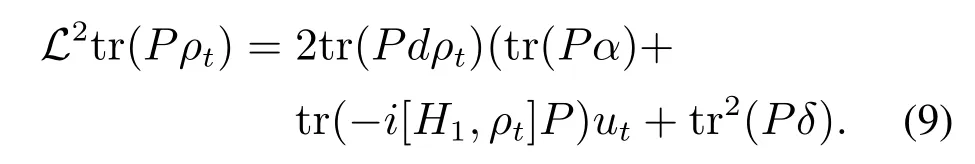
将式（6）和式（9）代入式（4）可得

其中:

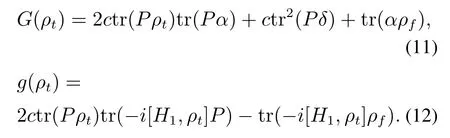
设计控制律为

其中kv ∈R且kv ＞0.将式（13）代入式（10）,可得

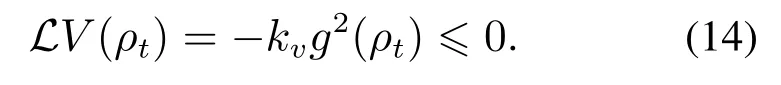
故控制律u(ρt)满足李雅普诺夫设计原理.

3.2 系统不变集分析及参数设计

根据拉塞尔不变集原理,对于任意初态,在控制律u(ρt)的作用下,系统状态会依概率收敛于不变集

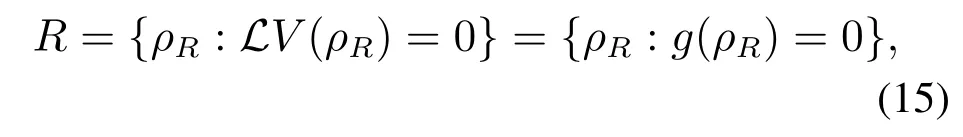
其中ρR为不变集R中的状态,即系统的平衡点.

对于目标态ρf,易知g(ρf)=0,因此ρf ∈R.根据李雅普诺夫定理和拉塞尔不变集原理,如果不变集R中只包含目标态ρf,控制律u(ρt)可以使系统状态从任意初态收敛到目标态.然而,不变集R中可能包含除目标态以外的其他状态,系统状态也会依概率收敛到这些状态.为了解决此问题,本文通过参数P和c的设计,确定系统的收敛域,使得此收敛域中只包含目标态,即系统状态在此收敛域中可以在控制律的作用下唯一地收敛到目标态.

根据设计需求,参数P和c的设计需满足两个条件:

1）使得目标态的李雅普诺夫函数值V(ρf）为0;

2）保证系统收敛域中的平衡点只包含目标态ρf.

为了满足要求1）,令:

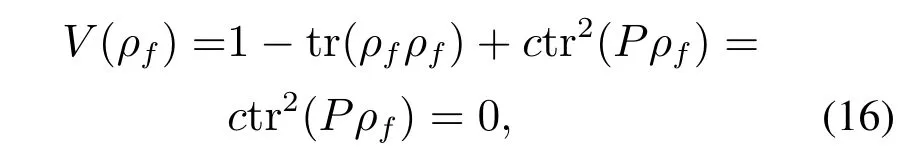
可得

为了满足要求2）,首先需分析不变集R中除目标态外的其他状态.当ρR/ρf时,系统的所有平衡点ρR满足条件

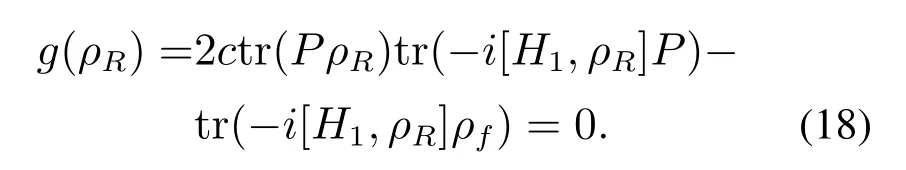
当系统的控制哈密顿量H1和目标态ρf确定时,方程（18）的解仅和参数P和c有关,即通过参数P和c的选取可以确定系统不变集中的平衡点,从而确定系统的收敛域.在第2.2节中,给出了本文控制的目标态形式,目的是为了保证方程（18）有可数个解,假设该方程除目标态ρf外还有m个解:{ρR1,ρR2,···,ρRm},则不变集R中的状态为R={ρR1,ρR2,···,ρRm,ρf}.

为了便于描述,定义:Vmax:=表示位于状态空间S中的状态ρ的李雅普诺夫函数最大值;Q＞θ:={ρ ∈S:θ ＜V(ρ)＜Vmax},Q≤θ:={ρ∈S:0 ≤V(ρ)≤θ},表示两类区域.令

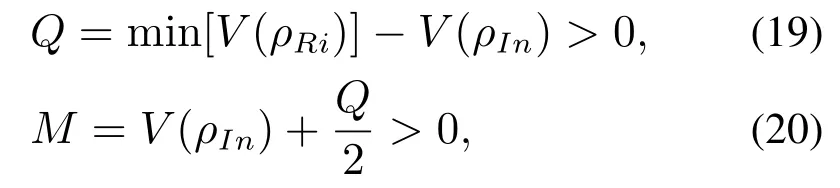
其中:ρIn=型单位矩阵,n为量子比特数;ρRi/=ρf,i=1,2,···,m为系统的i个平衡点.Q≤M即为所设计的收敛域,显然,0=V(ρf)＜M ＜min[V(ρRi)],即收敛域Q≤M中只包含目标态ρf.P和c的选取需使得式（19）和式（20）成立,即

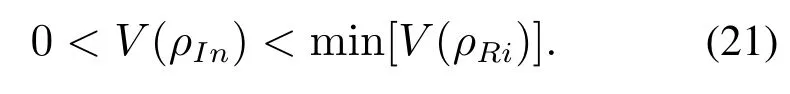
由此,式（17）和式（21）即为参数P和c的两个选取要求.

3.3 开关控制策略

由第3.2节分析可知,在系统的收敛域Q≤M中,系统状态可以在控制律u(ρt)的作用下收敛到目标态,为了使目标态可以从状态空间的任意初态收敛到目标态,设计了一个常量控制uc=1,用来驱动位于系统收敛域外的系统状态进入收敛域中,从而形成开关控制律ut,设计原理如图1所示.图中,状态空间S被分为3个区域:最外层的白色区域中间蓝色区域Φ和内层黄色区域Q≤M.

结合图1,本文设计的开关控制律ut的表达式为

对于系统不变集中的状态R={ρR1,ρR2,···,ρRm,ρf},只有目标态ρf位于收敛域Q≤M内,其他状态位于区域内（图1中假设系统不变集中有4个状态,且min[V(ρRi)]=V(ρR1)）.Φ是一缓冲区域,其作用是让位于边界附近的系统状态不会因为微小的扰动而使系统频繁切换控制律.系统的状态转移过程可依据状态所处区域的不同分为以下两种情况:

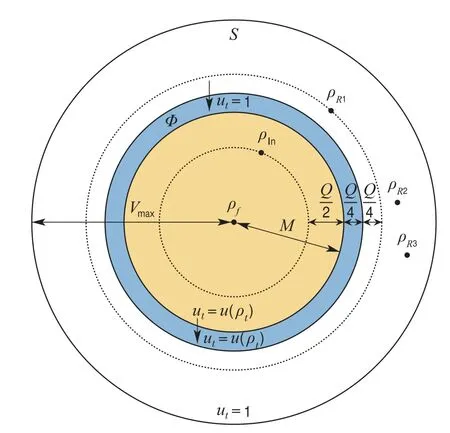
图1 开关控制律设计原理图Fig.1 Design principle of the switch control law

1）若系统状态一直处于Q≤M内,则控制律一直是u(ρt),由于Q≤M中只包含目标态ρf这一个平衡点,因此,系统状态会唯一地转移至目标态.

2）当只有常量控制uc=1时,系统状态会在有限时间内收敛到ρIn[15],因此,若系统状态在某一时刻位于Q≤M之外,则该状态在常量控制uc=1的作用下,一定可以转移至Q≤M内,并最终在控制律u(ρt)的作用下转移至目标态.

4 系统数值仿真实验及其结果分析

本节将所提出的控制方法（SFC）与文献[15]中的全局稳定控制方法（global stabilization control,GSC）进行性能对比的数值仿真实验,比较在不同目标态情况下的状态转移效果.笔者选取了2比特量子系统作为实验对象,进行两组实验:1）本征态到本征态的状态转移实验;2）叠加态到叠加态的状态转移实验.

在所有仿真实验中,系统参数设置为测量算符L=σz⊗I+I ⊗σz,相互作用时间Δt=0.01,测量效率η=0.5,随机噪声dW的幅值为0.05,采样总次数N=600,系统自由哈密顿量H0和控制哈密顿量H1分别为

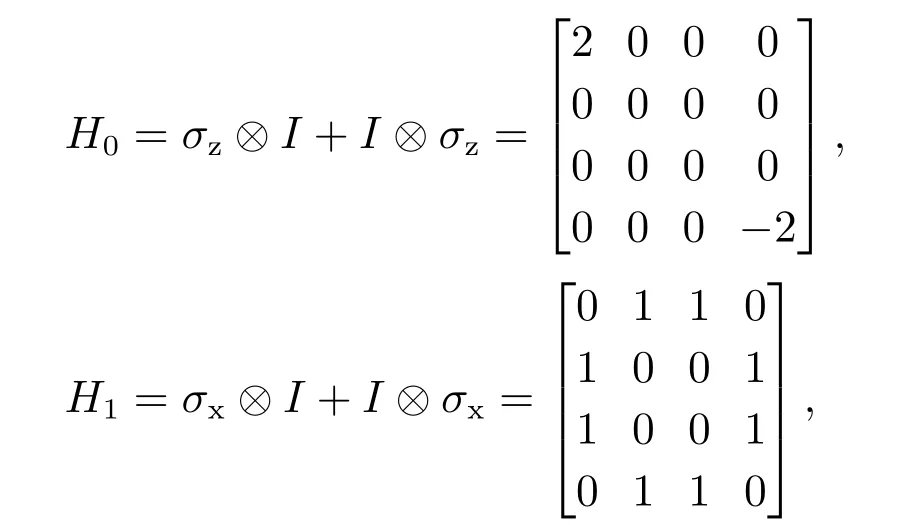
其中σx=和2×2型单位矩阵I为Pauli算符.对于状态转移效果的衡量,本文采用保真度指标Fidelity(ρt,ρf),其定义为

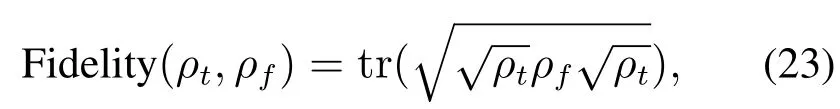
其中:ρt为系统的演化状态,ρf为状态转移的目标态.

4.1 本征态到本征态的状态转移实验

在本实验中,状态转移的初态设置为ρ0=diag{[1,0,0,0]},将目标态设置为ρf=diag{[0,0,0,1]},其中diag{[a,b,c,d]}表示对角元素分别为a,b,c,d的对角矩阵.结合参数P和c的选取条件式（17）和式（21）,选取

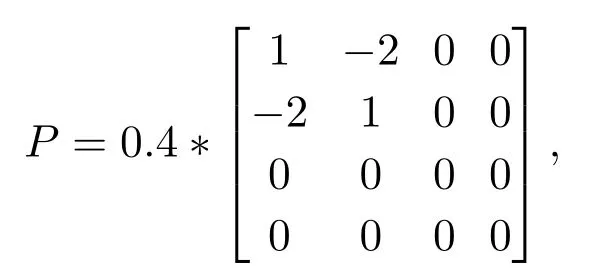
c=2,控制参数kv=2.

根据上述参数,通过式（18）计算,可以得到系统的4个平衡点分别为

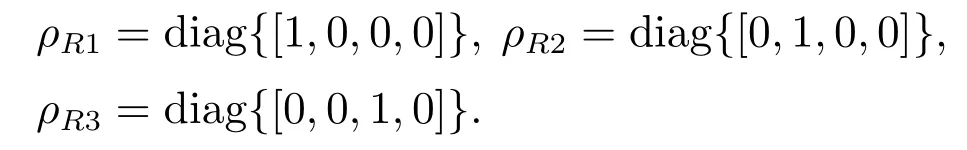
则根据式（19）和式（20）,可以计算出参数

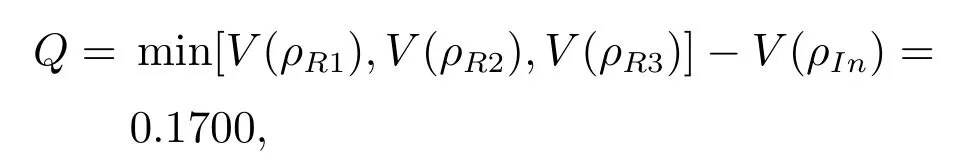
以及M==0.9150.所需要的控制律根据式（22）可以设计为

1）当V(ρt)＞0.9575时,ut=1;

2）当V(ρt)≤0.9150时,ut=u(ρt);

3）当0.9150＜V(ρt)≤0.9575时,若ρt是从区域Q≤0.9150进入Φ,则ut=u(ρt),否则ut=1.

数值实验结果如图2所示,其中:图2（a）为李雅普诺夫函数V(ρt)变化曲线;图2（b）为控制律变化曲线;图2（c）为无穷小算子LV(ρt)变化曲线;图2（d）为保真度变化曲线;图2（e）为利用SFC方法ρt中各对角元素变化曲线;图2（f）为利用GSC方法ρt中各对角元素变化曲线.图中,SFC为本文的控制方法,GSC为文献[15]中的控制方法.

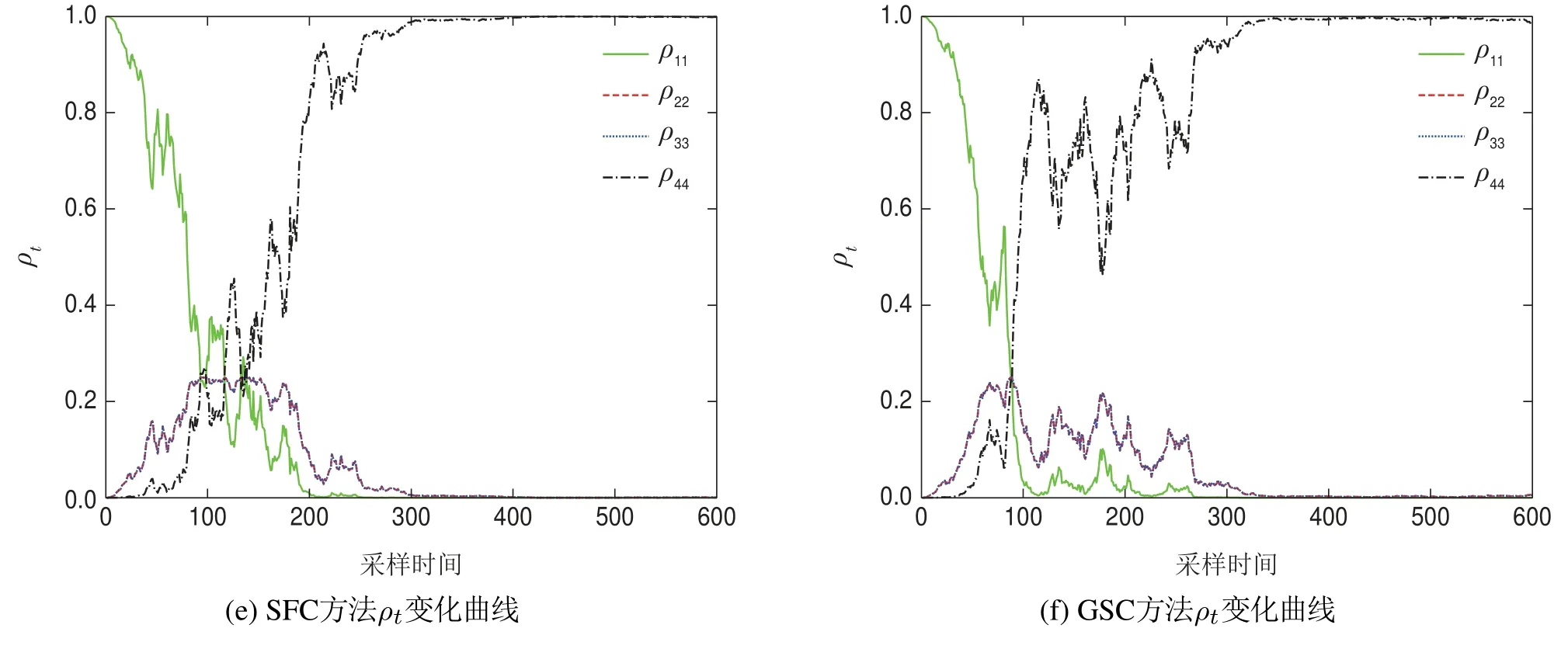
图2 本征态到本征态状态转移实验结果Fig.2 Experiment results from the eigenstate to the eigenstate

从图2中可以看出,SFC方法在65次演化之前,V(ρt)大于0.9150,因此控制为常量控制ut=1,在此控制下,状态ρt的变化最为迅速,即系统状态会迅速转移到Q≤0.9150区域内;此后的V(ρt)一直小于0.9150,故系统状态一直处于Q≤0.9150区域内,系统的控制一直为ut=u(ρt),在此控制下,系统状态缓慢变化并不断趋向目标态,状态转移的保真度可达到99%.实验的总体结论是:当状态转移的目标态是本征态时,虽然随机噪声给实验结果带来一定的不确定性,不过采用SFC方法和GSC方法都能实现控制任务,且控制效果大致相同.

4.2 叠加态到叠加态的状态转移实验

本实验中,状态转移的初态ρ0和目标态ρf均为叠加态

同样结合参数P和c的选取条件式（17）和式（21）,选取

c=2,控制参数kv=20.

根据上述参数,通过计算式（18）,可以得到系统的4个平衡点分别为

则参数

故本文设计的控制律（22）可写为

1）当V(ρt)＞0.8915时,ut=1;

2）当V(ρt)≤0.8832时,ut=u(ρt);

3）当0.8832＜V(ρt)≤0.8915时,若ρt是从区域Q≤0.8832进入Φ,则ut=u(ρt),否则ut=1.

数值实验结果如图3所示,其中:图3（a）为李雅普诺夫函数V(ρt)变化曲线;图3（b）为控制律变化曲线;图3（c）为无穷小算子LV(ρt)变化曲线;图3（d）为保真度变化曲线;图3（e）为利用SFC方法ρt中各对角元素变化曲线;图3（f）为利用GSC方法ρt中各对角元素变化曲线.图中,SFC为本文的控制方法,GSC为文献[15]中的本征态控制方法.

由图3可以看出,当状态转移的目标态是叠加态时,利用GSC方法无法从系统初态转移至目标态,不能完成控制任务.而本文提出的SFC方法是针对目标态为纯态的情况,可以完成控制任务.具体来看,系统状态的李亚普诺夫函数值V(ρt)一直小于0.8832,故系统状态一直处于Q≤0.8832区域内,系统的控制一直为ut=u(ρt),在此控制作用下,V(ρt)逐渐下降,状态转移的保真度逐渐上升并最终可达99%,实现了系统目标态的转移任务.

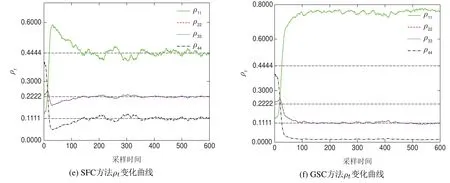
图3 叠加态到叠加态状态转移实验结果Fig.3 Experiment results from the the superposition state to the superposition state

5 结论

本文首次提出了一种对随机开放量子系统纯态的开关反馈控制方法.在此之前,人们仅可实现对随机开放量子系统的本征态或特殊混合态的控制.本文给出了有关随机开放量子系统纯态开关反馈控制方法的完整设计过程,下一步将把在线量子态估计应用其中,开发可应用于实际实验中的随机开放量子系统纯态开关反馈控制技术.