PMSM伺服系统线性自抗扰控制器的参数整定

许文波 魏泽宇 孔 伟潘 龙刘伟奇

（1.北京精密机电控制设备研究所,北京 100076;2.火箭军装备部驻北京地区第三军事代表室,北京 100076;3.航天伺服驱动与传动技术实验室,北京 100076）

1 引言

工程中伺服控制系统（permanent magnet synchronous motor,PMSM）多采用结构简单、易于实现、性能良好、对控制对象参数变化不敏感的PI控制器.为了提高和改善PMSM控制系统的跟踪性能及鲁棒性,近年来,国内外学者提出了多种先进的控制方式,如自适应控制、滑模变结构控制、自抗扰控制（active disturbance rejection control,ADRC）、神经网络控制、内模控制、二自由度控制等[1—10].其中ADRC于1998年由韩京清研究员正式提出,它将作用于被控对象的所有不确定因素均视为“未知扰动”,并利用对象的输入输出信息对其进行实时估计并给予补偿[11],使得ADRC不依赖于系统精确数学模型,具有很强的鲁棒性和实用性[12—13].特别是美国克利夫兰州立大学的高志强教授将非线性自抗扰控制器中的非线性环节线性化处理[14—15],提出了线性自抗扰控制（linear active disturbance rejection control,LADRC）,采用极点配置的思想将LADRC参数与带宽联系起来,极大简化了ADRC的参数整定方法,推动了自抗扰控制的工程实际应用发展[16—17].

后续有不少学者对LADRC的参数整定进行了研究.文献[18]将参数整定看做一个存在不确定性的闭环极点配置问题,并用根轨迹法对该问题进行了研究.文献[19]采用基于高阶控制器近似拟合的措施来获得LADRC的控制参数.由于此种方法并不局限于带宽法调参需使反馈控制器及扩张观测器极点配置在同一位置的限制,因此可以期望获得比带宽法更好的性能.文献[20]提出将PID参数转化为二阶LADRC参数的方法.该方法转化的LADRC参数以带宽形式表示,从而保留了传统LADRC简单易调的特性.文献[21]针对二阶ESO利用观测器带宽和控制器带宽给出了观测器和控制器的参数整定方法,但是文中参数整定方法只考虑了系统抗扰能力,未考虑系统的跟随性.文献[22]对于多输入—多输出系统研究了基于PID控制参数设计ADRC控制器的方法.

本文在文献[23]的基础上,以PMSM航天机电伺服系统为实例,给出了“位置—速度—电流”三闭环LADRC控制器的参数整定方法,思路为将PID控制器转换为自抗扰控制器,这样简化了自抗扰控制器的设计,将7个待整定参数减少为3个物理意义明确的待整定参数.首先利用极点配置的方法进行“P+P/I+P/I”控制器参数的设计.在此基础上,由于文献[24]证明了（extended state observer,ESO）的扰动观测中含有输出的积分项,从而说明使用ESO的控制器其整个控制的积分作用包含在扰动的估计及补偿里.因此将“P+P/I+P/I”控制器的速度环和电流环积分（I）环节替换为速度环线性扩张状态观测器（speed linear extended state observer,SLESO）和电流环线性扩张状态观测器（current linear extended state observer,CLESO）对扰动补偿.将原控制器改造为“P+P/SLESO+P/CLESO”结构的自抗扰控制器.ESO比I具有更好的性能,通过ESO将系统中的非线性扰动进行观测和补偿,将被控对象改造为近似线性的系统,可以降低控制器的控制难度,提升控制品质.仿真和实验证明了使用LADRC控制器的系统具有良好的鲁棒性,并最终在工程应用中取得了良好的效果.

扰动补偿是一把双刃剑,在提升系统抗扰能力的同时,也会将噪声补偿到控制指令中从而提升系统的噪声等级,这在一些特殊的应用领域无法满足指标.对于双惯量系统,扰动补偿也会诱发由负载惯量和轴弹性引起的较大振动.对此可以设计增益为1以下的观测器（谐振比控制）或者控制观测器的带宽[25].PMSM机电伺服系统由于电机转速一般由电机转角差分得到,噪声较大.所以本文对速度环外扰力矩和电流环反电动势两种扰动单独设计观测器并设置不同观测器带宽.这样对于使用转速信号的SLESO可以降低对外扰力矩观测的带宽,从而降低系统噪声.

2 问题描述

文献[23]中对如图1所示的航天机电伺服系统带动空气舵或喷管负载进行了建模,建立了非线性自抗扰模型.但是在实际工程应用中,非线性自抗扰控制方法参数难以整定,所以本文在文献[23]的基础上设计了“P+P/SLESO+P/CLESO”结构的线性自抗扰控制器.

图1 航天机电作动器带动空气舵和喷管的示意图Fig.1 Schematic diagram of aerospace electromechanical actuator driving air rudder and nozzle

在d-q旋转坐标系下,Ld=Lq=L,采用id=0控制,PMSM的电压方程、转矩方程、机械运动方程可分别表示如下

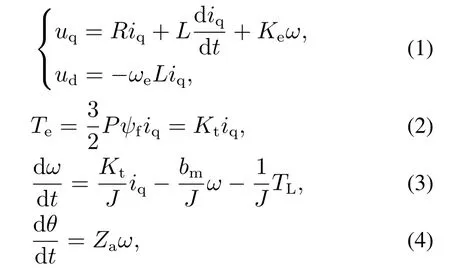
式中:uq,ud为d,q轴电压;iq为q轴电流;ψf为永磁体磁链;R,L为定子绕组电阻和电感;Ke为电机的反电动势常数;ωe为电机的电角速度;ω为电机的机械角速度;Kt为转矩常数;J为转动惯量;bm为电机粘滞摩擦系数;TL为负载转矩;Za为机电作动器电机转动角度到位置环反馈的减速比.

作为数字控制系统内环的电流环,主要实现d,q轴电流的快速跟随及电流限幅,其采样频率远高于位置环和速度环采样频率,具有较高的控制环路带宽,在本文中设逆变器的电压增益为Kinv,忽略滤波器及逆变器动态性能对电机转速特性的影响,电流和速度控制器均采用PI结构,位置环采用P结构,即

综合式（1）—（7）建立如图2所示的“P+P/I+P/I”控制器.图中Kinv为逆变器的电压增益.

图2 PMSM三闭环PI控制框图Fig.2 Block diagram of PMSM triple closed-loop PI controller

然后将速度环和电流环的积分环节（I）替换为ESO,改造为如图3所示的“P+P/SLESO+P/CLESO”结构的自抗扰控制器.

图3 PMSM三闭环线性自抗扰控制框图Fig.3 Block diagram of PMSM triple closed-loop LADRC controller

3 控制系统极点配置

3.1 电流环的零极点分析

电流环作为PMSM转速控制系统的内环,其动态响应特性直接关系到整个系统的动态性能.由图4可知,电流环中不仅存在电流反馈,还包括反电动势反馈,由于电流环的调节过程比速度环的变化过程快得多,所以研究对的作用时,可忽略反电动势的变化.因此到iq的控制框图和状态方程、输出方程如下:

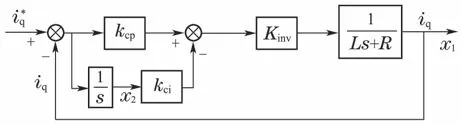
图4 PMSM电流环PI控制框图Fig.4 Block diagram of PMSM current PI controller

该系统完全可控.其零、极点特征方程分别为

由式（9）和式（10）,得电流环的零、极点如下:

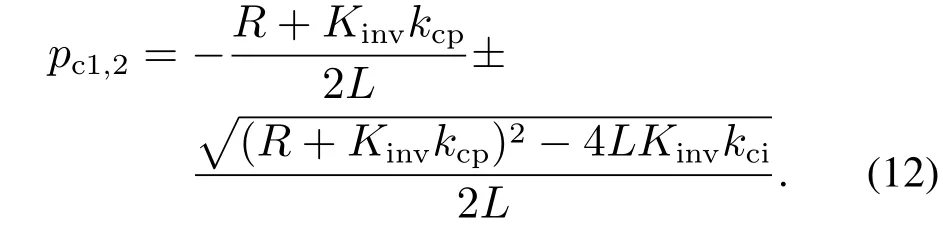
由式（12）可知,PI控制器的比例增益kcp决定了电流环极点与虚轴的距离,即决定了电流环的快速性;积分增益kci决定了电流环极点的虚部和闭环零点,极点虚部的影响系统的超调和振荡;电流环闭环零点的存在会缩短电流环的调节时间和增大其超调.

可以证明,当式（8）所示的PMSM电流环PI控制系统的一对极点为pc1=-a和pc2=-b,其中a,b均为正实数,且a ＞b时,可以通过极点配置来抵消或减小式（11）所示的系统零点对系统超调的影响.电流环的性能取决于极点pc1=-a,在研究速度环时,若把电流环等效为一阶惯性环节,其闭环带宽ωcb=a（rad/s）.

3.2 电流环的结构重构

由于电流环的调节过程比速度环的变化过程快得多,在分析设计速度环时可将电流环的闭环传函近似看成1或将其等效为一阶惯性环节.

若将电流环等效为一阶惯性环节式,为了保持速度环为全状态反馈,本文提出一种对电流环控制框图进行重构的方法,重构后的电流环控制框图见图5.

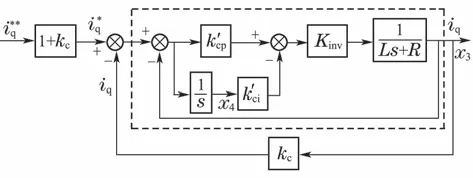
图5 PMSM电流环PI控制结构重构Fig.5 Block diagram of restructure for PMSM current PI controller

3.3 速度环的极点配置

将电流环内环用式（13）所示的一阶惯性环节替代,构成全状态反馈PMSM速度环控制框图,见图6.

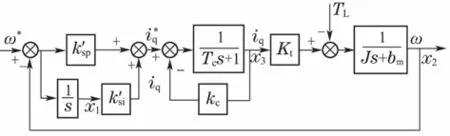
图6 全状态反馈PMSM速度环PI控制框图Fig.6 Block diagram of PMSM speed PI controller with full-state feedback

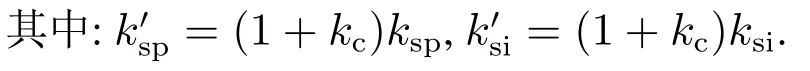
由图4可写出速度环状态方程和输出方程如下:

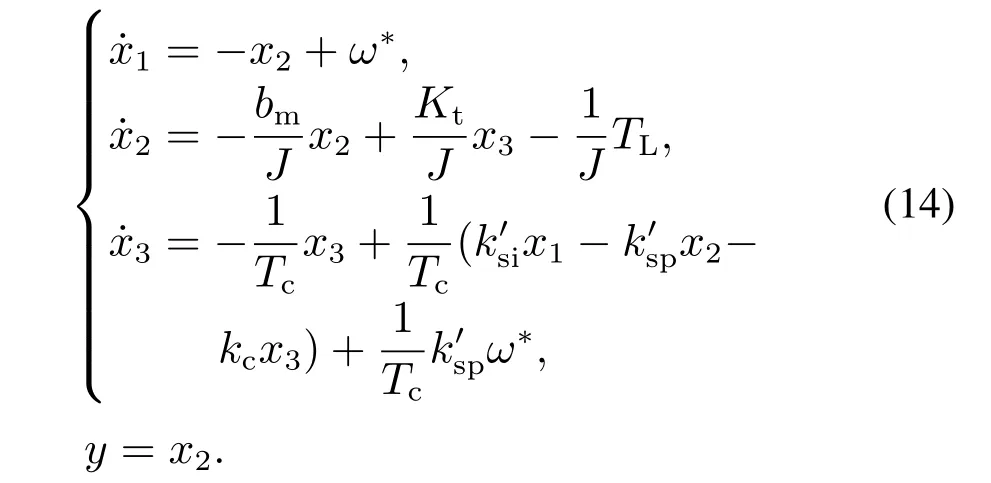
速度环零、极点特征方程分别为

速度环PI控制器将引入一负实闭环零点,如下:

假设该系统的3个极点分别为ps1,ps2和ps3,且ps1与虚轴的距离远小于ps2和ps3与虚轴的距离.可以证明,对于式（14）所示的PMSM转速PI控制系统,若该系统存在一负实极点与虚轴的距离远小于其它两极点与虚轴的距离,则该极点与式（17）所示的系统零点能够基本抵消,即通过对速度环极点配置,可以通过选取靠近虚轴的负实极点ps1来抵消闭环零点对速度环性能的影响,速度环的性能主要取决于极点ps2和ps3.

3.4 结构重构-还原

kc的引入改变了PMSM机电系统原PI控制的结构和参数,为保持原控制结构的不变性,需要根据整定的参数及系统重构关系,对系统原PI控制参数按式（18）进行还原

根据式（16）,有

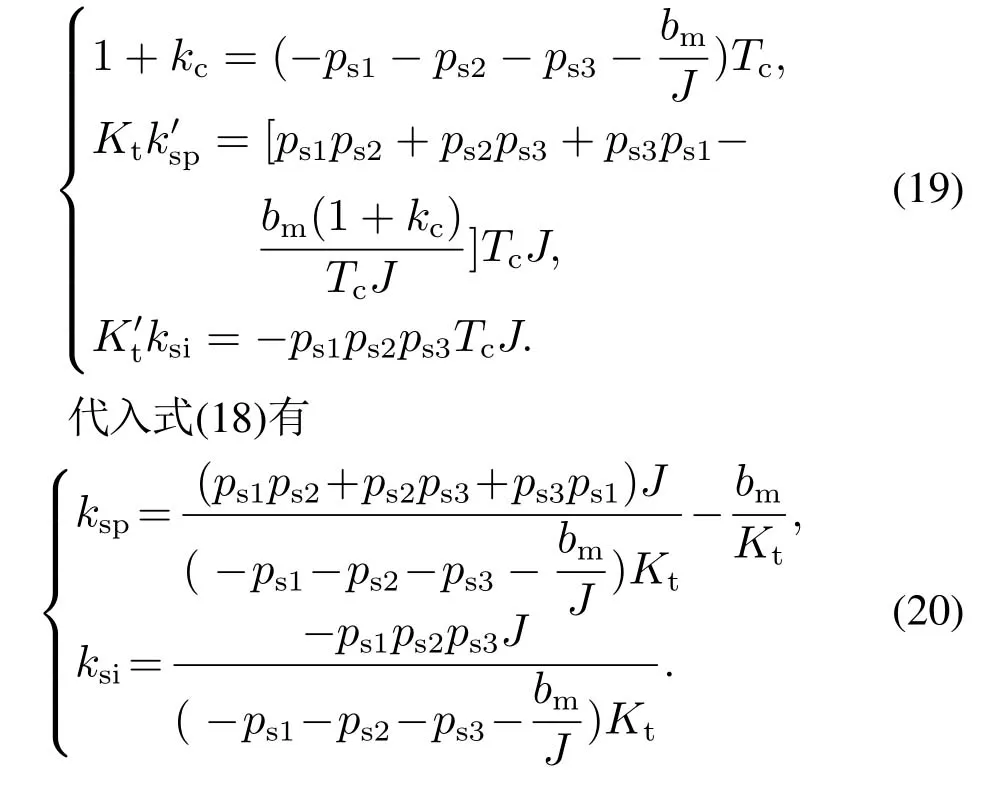
由式（19）和式（20）可知,经过电流环结构重构,速度环控制参数ksp和ksi只与其期望极点及电机、负载的机械参数相关,与其电流环及电气参数无关.

由式（21）可知,经过结构重构—还原后,电流环控制参数kcp和kci取决于速度环期望极点及产品固有参数,与预置极点基本无关,但预置极点影响电流环的快速性及超调.

经过结构重构—还原,双闭环PMSM速度环PI控制框图仍如图2所示中速度环控制.控制参数ksp,ksi,kcp和kci仅与速度环期望极点ps1,ps2,ps3及电流环极点相关,且ps2,ps3决定了速度环的主要性能,和pc2的选取可以分别用来调节速度环及电流环的跟踪速度和超调量.

3.5 位置环的极点配置

分析位置环极点时将速度环和电流环简化为比例为1的环节,其控制框图如图7.

图7 位置环框图Fig.7 Block diagram of position control

位置环传递函数

可求得位置环极点为

其闭环带宽ωpb=Zakpp（rad/s）.

4 线性扩张状态观测器的设计

4.1 速度环观测器设计

根据式（3）,PMSM速度环动态方程

设计如下速度环线性扩张状态观测器（SLESO）:

SLESO增益[βs1βs2]的选取可以采用极点配置来确定.

此时,速度环控制律可设计为

根据式（13）将电流环简化为一阶惯性环节,结合式（1）—（2）（13）（24）—（25）,可得到速度环观测器对外扰力矩的观测和外扰力矩的传递函数为

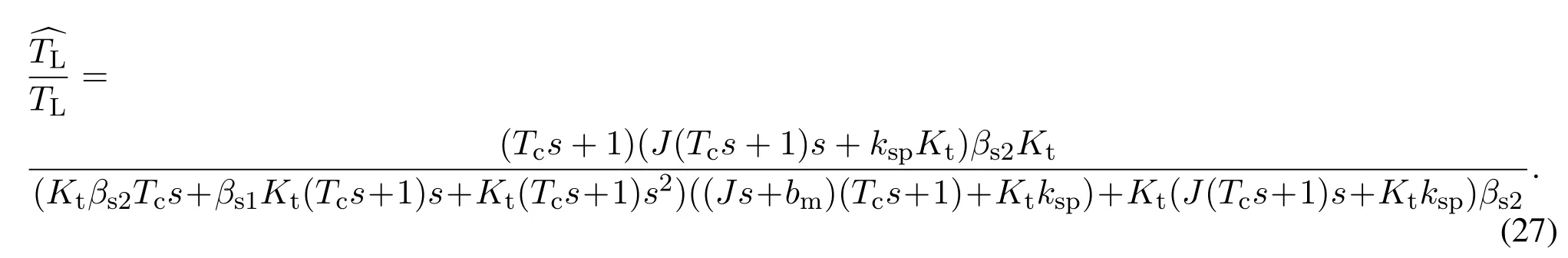
由于电流环带宽远高于速度环带宽,故令Tc≈0.则式（27）可写为

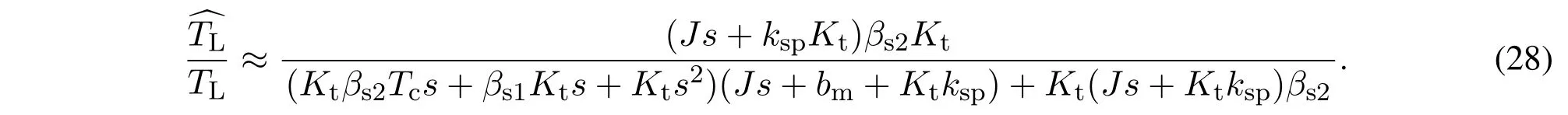
通过MATLAB进行频率特性分析可以得到其带宽为ωso.

4.2 电流环观测器设计

同样根据式（1）,可对q轴电流环控制器设计扩张状态观测器（CLESO）和控制律.

式中Ω=ωKe为反电动势.

设计如下电流环线性扩张状态观测器（CLESO）:

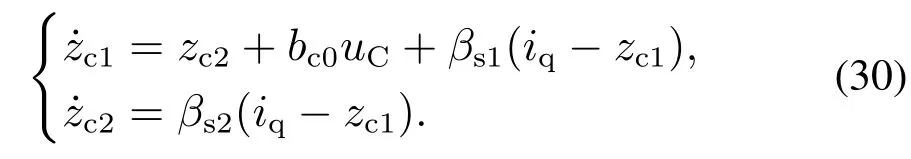
CLESO增益[βc1βc2]的选取同样采用极点配置来确定.

电流环控制律可设计为

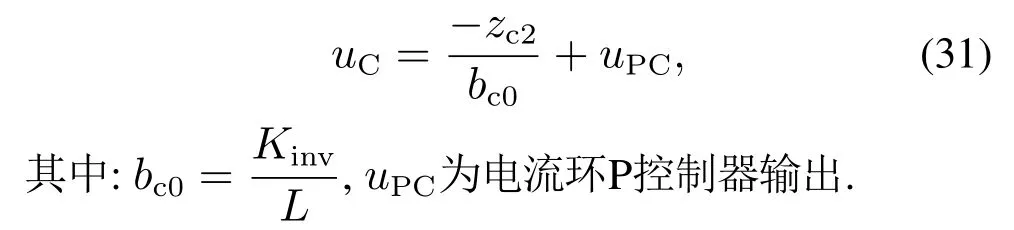
结合式（29）（30）,可得到电流环观测器对反电动势的观测和反电动势的传递函数为

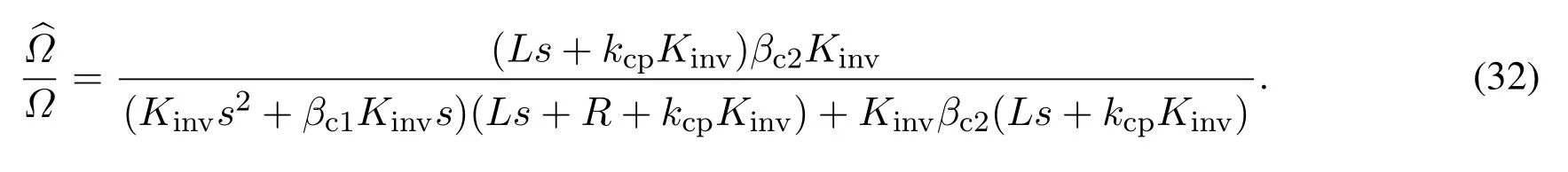
通过MATLAB进行频率特性分析可以得到其带宽为ωco.

PMSM速度环LADRC控制框图如图8所示.

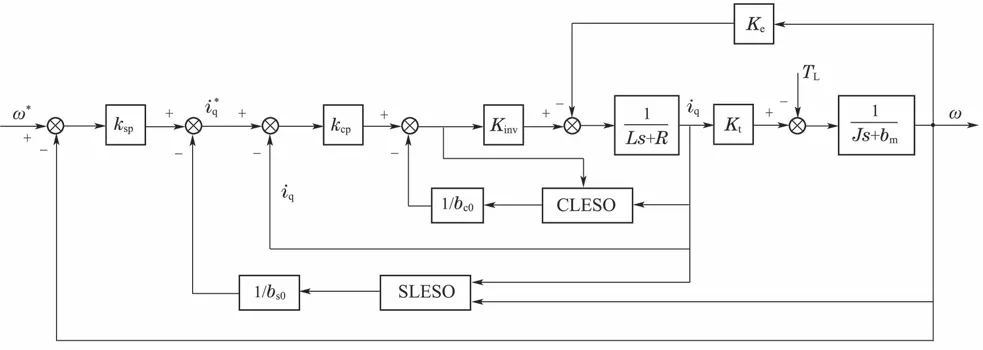
图8 PMSM速度环LADRC控制框图Fig.8 Block diagram of PMSM speed controller with LADRC

4.3 小结

综合第3,4节所述,控制系统7个待调参数kpp,kcp,ksp,βs1,βs2,βc1,βc2的配置可以转化为pp,ps1,ps2,ps3,ωso,ωco的参数配置,其中ps1,ps2,ps3的主导极点为ps2,ps3,且可以配置为对偶极点,ωco按实际调试的经验一般取2～3倍ωso,ωso由速度环观测器增益[βs1βs2]决定,而[βs1βs2]可先配置好极点然后用Acker—mann公式求解,电流环观测器同理.所以最终只需要配置pp,ps2,ωso,如表1中所示.这3个参数均有明确物理意义,易于调节.值得注意的是,控制器中在输入输出处要设置限幅,这些限幅参数需要与系统性能要求和硬件自身能力匹配,否则会影响系统性能甚至损坏功率器件.

表1 参数整定方法Table 1 Parameters tuning method

参数整定流程如图9所示.

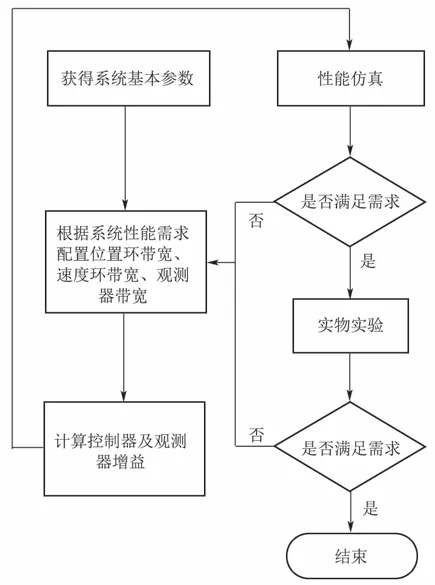
图9 参数整定流程图Fig.9 Flow chart of parameter setting

5 稳定性分析

系统的状态方程为

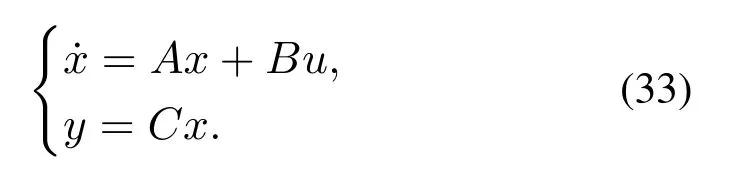
式（33）中

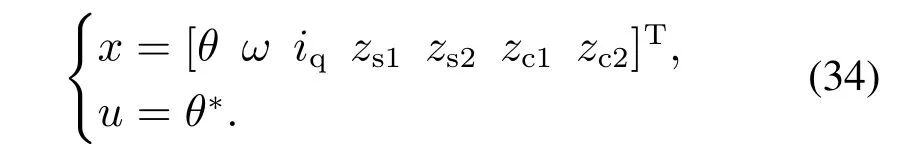
综合式（1）—（4）（25）（30）可得

根据李雅普诺夫稳定性,如果系统特征矩阵的特征值均出现在s平面的左侧（含虚轴）,则可认为闭环系统是稳定的.在该系统中,系统给定输入信号θ*总是有界的,而在实际系统中扰动量不能无限增大,所以可以认为是可微且有界的,则该系统的稳定性就取决于状态矩阵A的特征值大小.通过配置kpp,kcp,ksp,βs1,βs2,βc1,βc2参数的大小可以保证闭环系统稳定,具体分析过程在第6.1节阐述.

6 仿真分析与实验验证

利用MATLAB中的SIMULINK模块进行仿真,PMSM机电伺服参数具体如下:

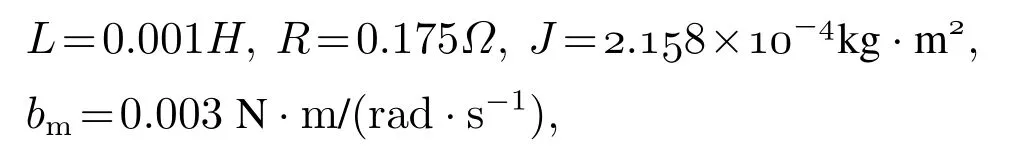
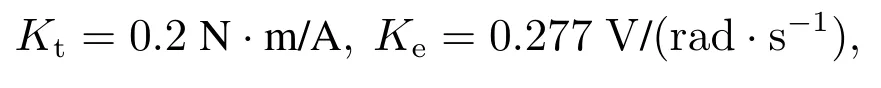
取逆变器放大系数Kinv=158.4 V.

6.1 系统参数设计

仿真时取系统希望极点（pp,,ps1,ps2,ps3）为（-82.5,-1.25,-150,-800+600i,-800—600i）,可求得系统控制参数为kpp=140,ksp=0.6752,ksi=0.8423,kcp=0.0101,kci=1.5163.调整CLESO和SLESO极点位置使其对外扰观测的带宽分别为ωco=251.3 rad/s（40 Hz）和ωso=125.7 rad/s（20 Hz）,对 应的极点分别取（-263.2±197.4i）（-120±90i）.此时βc1=526.4,βc2= 108241;βs1=240,βs2=22500.观测器对外扰的频率特性见图10和图11.

图10 速度环观测器对外扰力矩观测伯德图Fig.10 Bode diagram of external disturbance moment observation of SLESO

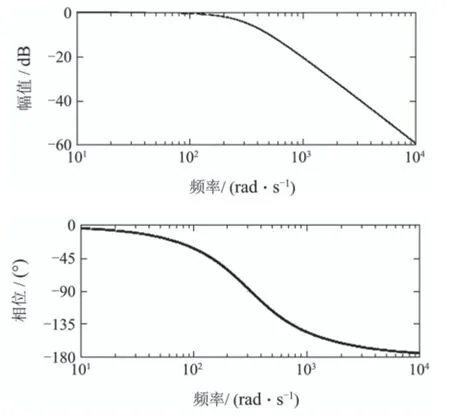
图11 电流环观测器对反电动势观测伯德图Fig.11 Bode diagram of back electromotive force observation of CLESO

将实例中的系统各参数代入式（33）中求解系统特征矩阵A的特征值为

由特征矩阵A的特征值可以认为闭环系统是内部稳定的.

为了进一步分析系统的稳定裕度,由式（33）求得系统开环特性并作伯德图,如图12所示.可以到系统的幅值裕度为28.8 dB,相角裕度为77.5°.可见系统有足够的稳定裕度.

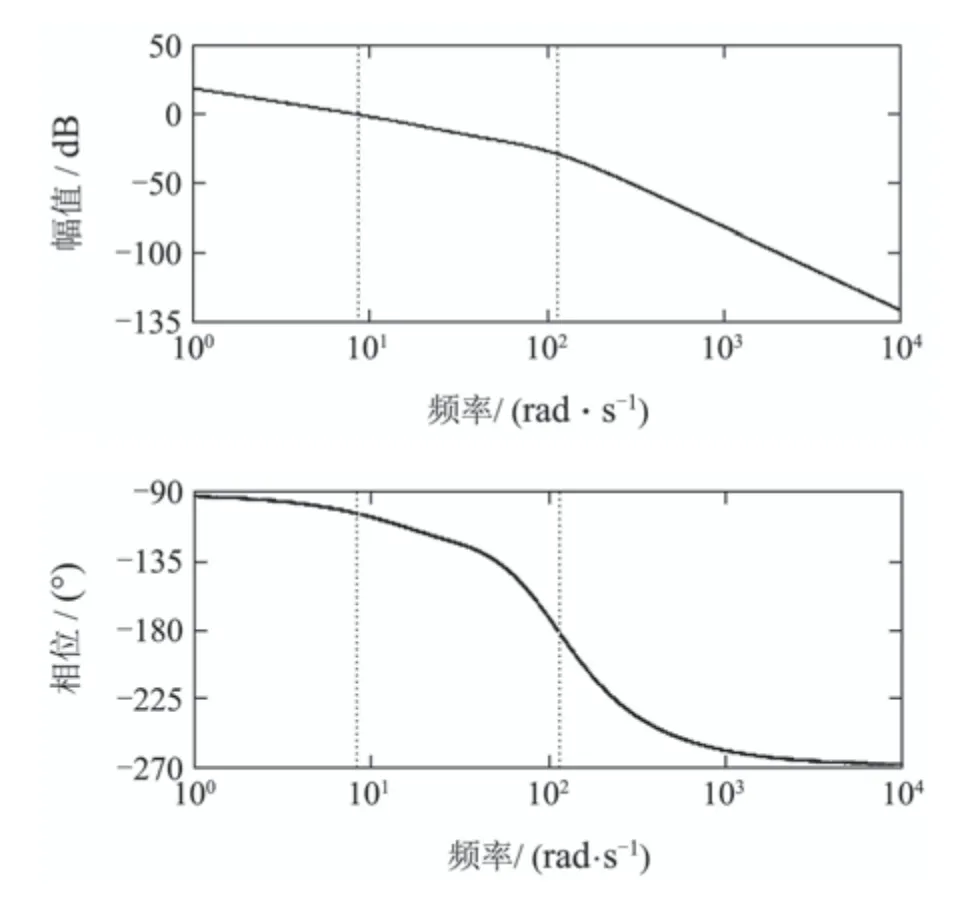
图12 系统开环特性伯德图Fig.12 Bode diagram of system open-loop characteristics

6.2 速度环阶跃响应及抗扰仿真分析

给定转速为1000 r/min,系统采用不同控制策略时的阶跃响应如图13所示.仿真结果表明,单独使用CLESO与同时使用SLESO和CLESO结果接近,能够补偿反电动势造成的跟随静差.单独使用SLESO由于无法补偿反电动势所以跟随存在静差.“P/SLESO+P/CLESO”控制器与“P/I+P/I”控制器其相比,上升时间由36 ms提高到了24 ms.

图13 速度环阶跃响应Fig.13 Step response of speed loop

ps2,ps3极点的虚部与实部的比值为0.75,接近最佳阻尼比系数,但是由于反电动势的存在,系统并未出现较大的超调.“P/I+P/I”控制器超调量为0.4%,“P/SLESO+P/CLESO”控制器超调为0%.

在系统进入稳态后对电机突加1 Nm负载力矩时电机速度环的阶跃响应如图14.“P/I+P/I”控制器在3 s后才回归稳态,若加大速度环的积分增益kci能够提高系统抗负载扰动的能力,但会加大系统的超调;“P/SLESO+P/CLESO”控制器仅在0.032 s后就快速回归稳态.

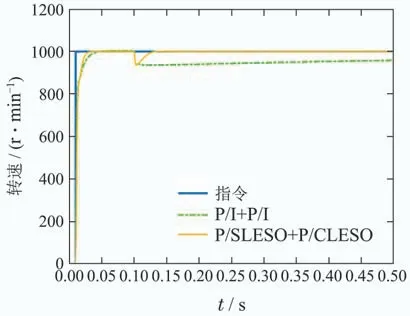
图14 动态跟踪过程中突加1 Nm负载速度环阶跃响应Fig.14 Step response with suddenly increase 1 Nm load during dynamic tracking of speed loop

图15为系统零—极点分布图,在进行系统零极点配置时未考虑反电动势对系统的影响,并对控制参数求解算式进行了简化,系统的极点并不能与期望理想极点完全重合.仿真结果表明,仅对速度环的抗扰控制（SLESO）不影响系统零—极点分布,其零—极点分布与无抗扰控制时重合;电流环的抗扰控制（CLESO）能够影响系统零—极点分布,并将系统的零点与极点基本对消,仅对电流环抗扰控制系统与电流环和速度环双抗扰控制系统的零—极点重合.

图15 双闭环PMSM转速系统零—极点分布图Fig.15 Pole-zero map of PMSM driving system

通过仿真可以得出以下结论:

1）电流环的自抗扰控制能够观测和补偿反电动势等因素对电流环的影响,大幅提高电机转速的响应速度,但是无法克服负载力矩的扰动;

2）速度环的自抗扰控制能够有效克服负载力矩扰动对电机转速的影响,但无法改变电机转速的响应速度;

3）采用“P/SLESO+P/CLESO”结构线性自抗扰控制的电机转速系统的零—极点更能接近期望零—极点,系统响应能够跟随期望输出.

6.3 位置环阶跃响应及抗扰仿真分析

利用文献[23]中的仿真系统,在0.1 s处给系统输入5°幅值的阶跃响应,对负载在1 s处加入1000 N·m（折合到电机轴上约1.85 N·m）的外扰力矩,“P+P/SLESO+P/CLESO”结构的LADRC控制器最大扰动角度变化为输入角度的0.22%,在0.027 s后扰动角度缩小到输入角度的0.1%以下,而“P+P/I+P/I”结构的PI控制器最大扰动角度变化为输入角度的0.42%,在1.11 s后扰动角度缩小到输入角度的0.1%以下.结合图6和式（20）可知,提高速度环积分ksi可以提高系统抵抗外扰力矩的能力,所以将ksi分别乘系数2和3,即ksi=1.685,ksi=2.527.扰动角度缩小到输入角度0.1%以下的时间分别缩短到0.55 s和0.38 s,但是系统超调由0.14%变至0.36%和0.47%,说明LADRC控制器效果相较PI控制器具有对外扰鲁棒性好且无超调的优势.结果如图16所示.

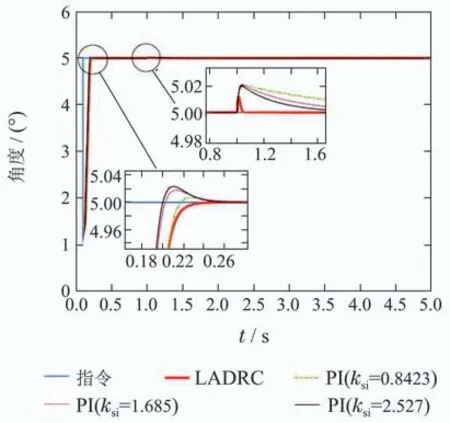
图16 动态跟踪过程中突加1000 N·m负载位置环阶跃响应Fig.16 Step response with suddenly increase 1000 N·m load during dynamic tracking of position loop

6.4 蒙特卡洛分析

利用文献[23]中的仿真系统,同样给系统输入5°幅值的阶跃响应,同时对电机力矩系数、电机电阻、电机电感、电源电压、机电作动器支撑刚度等13个系统运行中容易变化的参数进行150组±20%的随机拉偏.对比ADRC控制器和PI控制器的超调、上升时间和ITAE（误差绝对值对时间的积分）指标.图17所示为ITAE指标全行程统计,可以看出LADRC控制器在系统参数摄动时,3个指标的散差明显小于PI控制器.

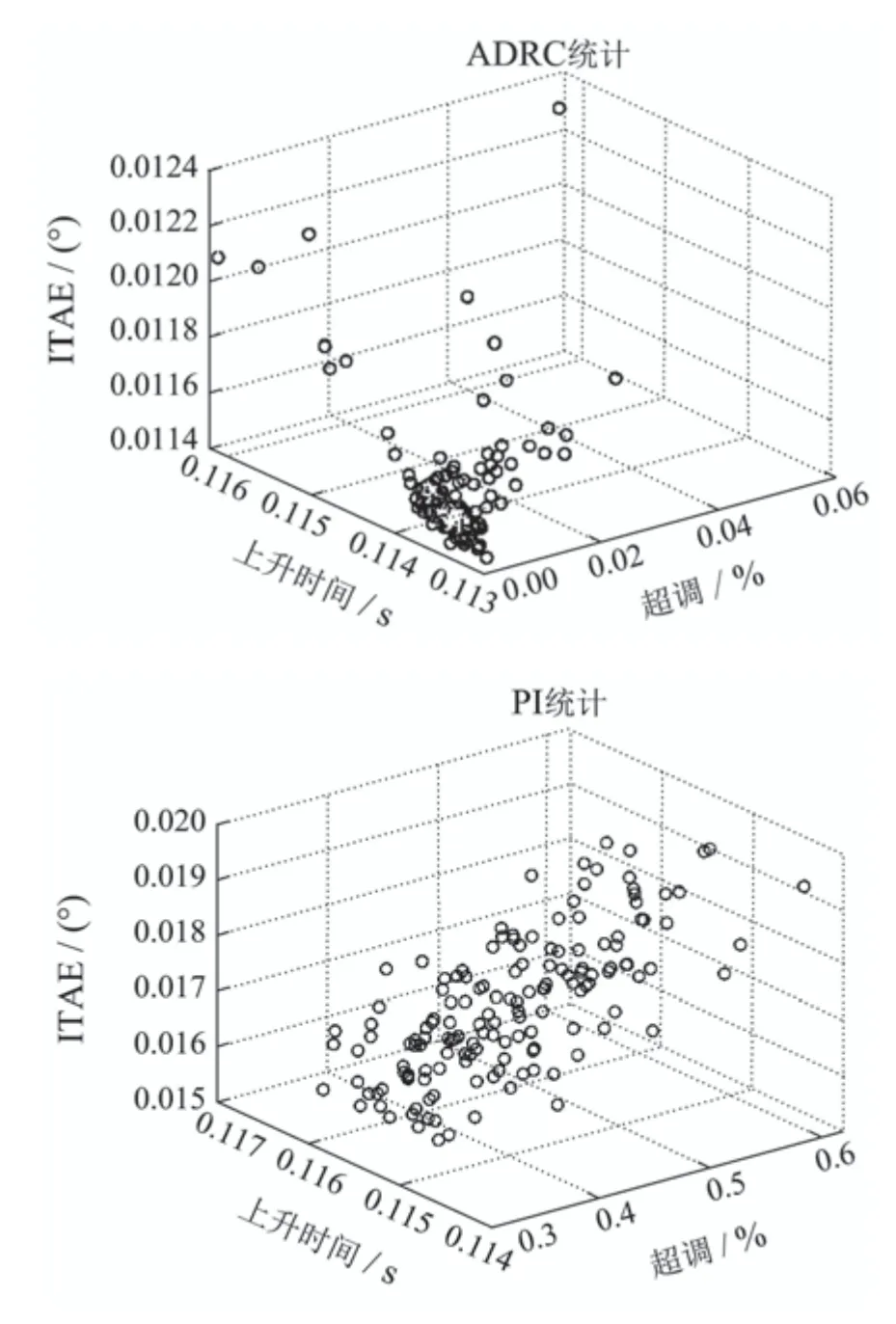
图17 LADRC控制器和PI控制器的超调、上升时间和ITAE（全程）Fig.17 Overshoot,rise time and ITAE of LADRC controller and PI controller（full range）

图18所示为ITAE指标只统计稳态值,可以看出PI控制器ITAE为10-3量级,而LADRC控制器ITAE为10-5量级.

图18 LADRC控制器和PI控制器的超调、上升时间和ITAE（稳态）Fig.18 Overshoot,rise time and ITAE of LADRC controller and PI controller（steady state）

6.5 实验验证

本文实验使用的PMSM机电伺服系统（图19）与文献[23]中使用的相似,由控制驱动器、机电作动器、测试仪、电源和负载组成,不同的是:a）在电机轴端增加了可以提供2.8 N·m 的摩擦式电磁锁用来在非工作状态下锁紧机电作动器;b）负载是纯摩擦负载,无弹性负载.控制器参数与仿真分析所用参数保持一致.

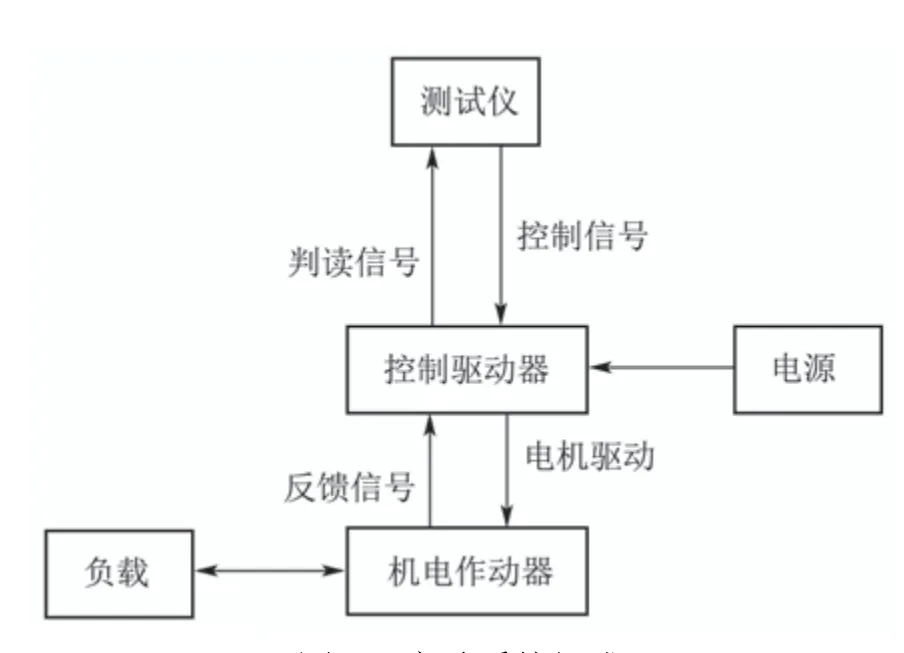
图19 实验系统组成Fig.19 Experimental system composition

如图20所示,在负载摩擦力矩400 N·m（折算到电机轴端为0.74 N·m）的条件下在1 s处给系统输入4.8°的阶跃信号,可以看到系统对指令进行了无超调的跟随.图20实验系统的上升时间和超调量与图16仿真系统接近,证明了仿真模型有效.

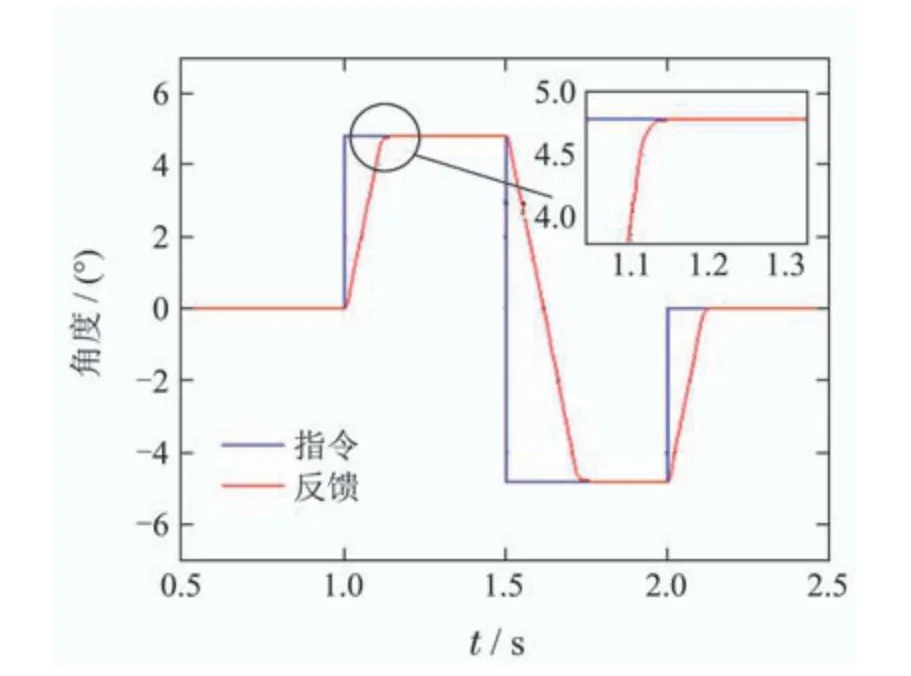
图20 PMSM机电伺服系统阶跃响应Fig.20 Step response of PMSM electromechanical servo system

图21和图22分别是系统响应阶跃信号时SLESO对外扰力矩和CLESO对反电动势的观测曲线.图22中反电动势观测值在±95 V处进行了限幅,防止系统在控制电路通电工作而功率电路未通电工作的情况下（功率逆变器有控制输入却无电压输出）,反电动势观测值无限增大（相当于PI控制中积分环节限幅）.

图21 速度环扩张状态观测器对外扰力矩观测曲线Fig.21 External disturbance torque observation curve of the SLESO

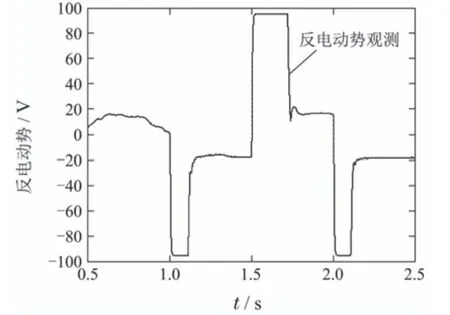
图22 电流环扩张状态观测器对反电动势观测曲线Fig.22 Back-electromotive force observation curve of CLESO

为了验证速度环观测器对外扰力矩观测的有效性,本文分别在电磁锁解锁和落锁状态下向机电作动器发送2°幅值,0.159 Hz（1 rad/s）,1.5周期的正弦波指令,同时读取速度环观测器观测值,如图23、图24所示.电磁锁解锁状态测量外扰力矩峰值为1.148 N·m,电磁锁落锁状态测量外扰力矩峰值为3.908 N·m.可以得到电磁锁力矩为3.908—1.148=2.76 N·m,与机电作动器装配时力矩扳手测量值一致,说明速度环观测器对外扰力矩进行了有效观测.

图23 PMSM机电伺服系统正弦波响应Fig.23 Sine wave response of PMSM electromechanical servo system

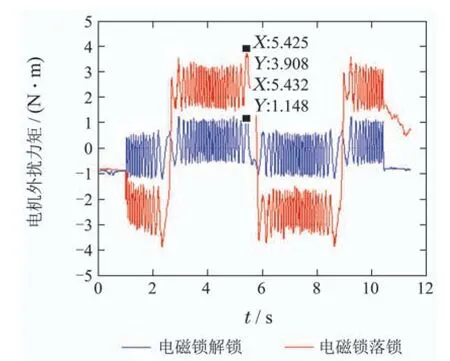
图24 速度环观测器对外扰力矩的观测值Fig.24 The observed value of external disturbance moment of SLESO

为了验证LADRC控制器相较于PI控制器有更好的动态性能,本文在无外部负载条件下分别对PI控制器和LADRC控制器在电磁锁解锁和落锁状态下进行以0°为中心幅值为1°的扫频实验,实验结果见表2和表3.从表2可以看出,PI控制器在落锁状态下动态性能变差.从表3可以看出,LADRC控制器在落锁后动态性能未变差,而且跟随性反而有提高,说明基于LESO的扰动补偿对相位有补偿作用.

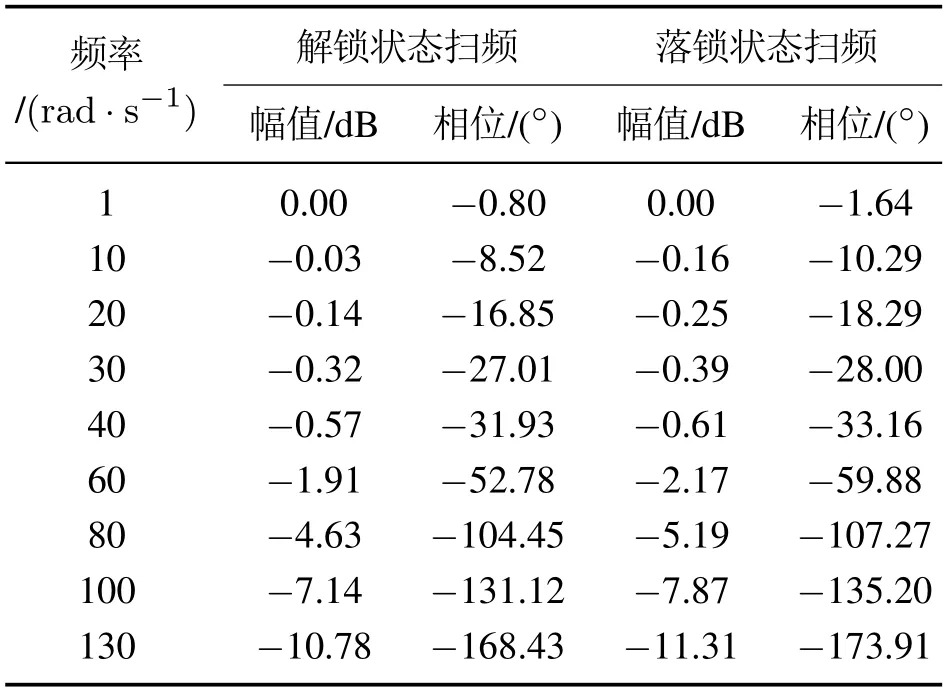
表2 PI控制器电磁锁解锁—落锁状态扫频对比Table 2 Comparison of PI controller’s scanning frequency for electromagnetic lock unlocking and locking state

表3 LADRC控制器电磁锁解锁-落锁状态扫频对比Table 3 Comparison of LADRC controller’s scanning frequency for electromagnetic lock unlocking and locking state

本文使用的机电作动器电机最大输出力矩为17.5 N·m,电磁锁摩擦力矩为2.76 N·m,电磁锁摩擦力矩为电机最大输出力矩的15.7%,在这样的摩擦负载扰动情况下,使用LADRC控制器的机电伺服系统仍然能够保证动态性能稳定,证明了LADRC控制器优异的鲁棒性.

为了进一步验证LADRC作动器对扰动的鲁棒性,文本调整CLESO和SLESO极点位置使其对外扰观测的带宽分别为ωco=754.0 rad/s（120 Hz）和ωso=377.0 rad/s（60 Hz）,并在不同外部摩擦负载力矩下对PMSM机电伺服系统进行扫频实验,实验结果如表4.可以看出:a）使用LADRC控制器的伺服系统同样保持了动态性能的稳定;b）提高观测器带宽后,系统相位超前于表3,但是实验现场伺服系统噪声要高于ωco=251.3 rad/s（40 Hz）和ωso=125.7 rad/s（20 Hz）的情况,在对观测器带宽进行整定时要考虑到此因素.

表4 LADRC控制器对不同摩擦负载的扫频对比Table 4 Comparison of LADRC controller’s scanning frequency for different friction loads

6.6 力矩波纹分析

由图24可以看出,速度环观测器对外扰力矩的观测值存在明显的力矩波纹,对U相电流、iq电流、转速的实测值和频谱进行分析得到图25、图26和表5所示结果,结果显示U相电流在5～15 Hz内的频点在iq电流和转速频谱中均可找到对应的频点,且能量最高频点均为11.78 Hz,表明相电流频率以谐波的形式加在了iq电流和电机转速频谱的基频上,原理可参考文献[26]对相电流谐波引起力矩波纹的分析,主要原因有相电流反馈系统中的失调和增益误差等.此外,图21中伺服对阶跃信号响应观测到的力矩没有力矩波纹,原因是阶跃信号的相电流谐波幅值与iq电流和电机转速基频幅值相比很小,所以力矩波纹现象不明显,限于篇幅限制,此处本文不作过多分析.

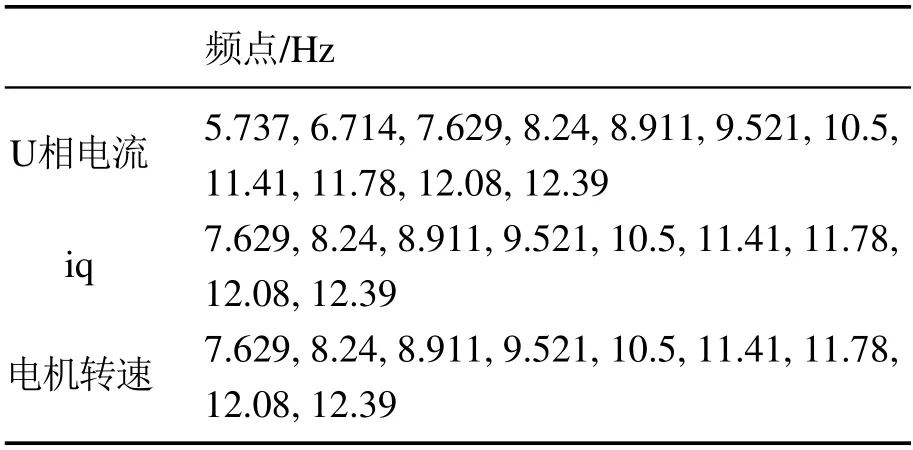
表5 U相电流、iq电流、转速在5～15 Hz的频点Table 5 Frequency points of U phase current,iq current and speed between 5～15 Hz

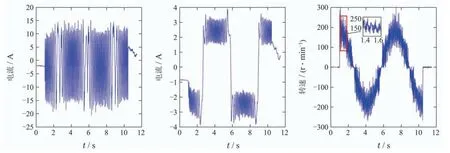
图25 U相电流、iq电流、转速实测值Fig.25 Measured values of U phase current,iq current and speed

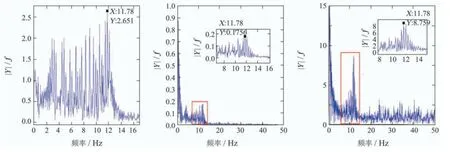
图26 U相电流、iq电流、转速频谱分析图Fig.26 Spectrum analysis diagram of U phase current,iq current and speed

7 结论

首先,本文以PMSM航天机电伺服系统为实例提出了一种将“P+P/I+P/I”结构的PI控制器改造为“P+P/SLESO+P/CLESO”结构LADRC控制器的方法,并且通过极点配置给出了参数整定规则,将LADRC控制器中的7个待整定参数转换为3个物理意义明确的待整定参数,降低了参数整定难度.其次,文本对研究对象进行了状态空间描述并给出了闭环系统稳定的条件.最后通过仿真和实验的方法对LADRC控制器的快速性和鲁棒性进行了验证,并在实验中发现基于ESO的扰动补偿可以改善被控对象频率特性的相位.