基于低差异序列与快速扩展随机树融合算法的机械臂路径规划

代 伟 李创业 杨春雨 马小平

（1.中国矿业大学信息与控制工程学院,江苏徐州 221116;2.中国矿业大学地下空间智能控制教育部工程研究中心,江苏徐州 221116）

1 引言

机器人路径规划自20世纪70年代提出以来,逐渐成为机器人学的重要研究领域.而机械臂路径规划问题是其重要内容.传统工业生产中机械臂主要用于单一流水线任务,其运行操作依赖于操作工人的示教编程,效率低且适应性差.而随着工业生产环境变得越来越复杂,就更需要机械臂能够自主规划出一条无碰撞路径以适应不同的环境.针对这一问题国内外学者提出了一些可用于机械臂路径规划的方法,主要有人工势场法[1]（artificial potential field,APF）,A*算法[2],遗传算法[3]（genetic algorithm,GA）,快速扩展随机树[4—5]（rapidly-exploring random tree,RRT）等.人工势场法和A*算法在路径规划时虽然能够满足最优性和实时性要求,但人工势场法极易陷入局部极小值点[6],A*算法存在内存开销大,运行时间长,累计转折角度大等问题[7].遗传算法具有很强的自适应性和学习性,但其进化速度容易受到参数的影响,且运算时需要占用大量的存储空间[8].RRT算法是一种基于随机采样的路径规划方法,其不需要对状态空间进行预处理,具有搜索速度快,便于处理约束等特性,能有效解决复杂环境下路径规划的问题,近年来被广泛应用于机器人路径规划领域.但标准RRT存在一些固有的缺陷[9]:1）盲目的随机采样导致算法无谓地耗费较大代价,使得收敛速度变慢;2）算法的随机性导致生成的路径不平滑,难以被机械臂直接执行.

针对标准RRT算法的上述不足,改进算法不断被提出以适应不同的应用环境.其中,文献[10]提出了RRT*算法,在RRT节点扩展基础上添加随机几何图与剪枝优化理论,确保随机树的节点都能收敛到当前最优值.文献[11]将双向人工势场与RRT*相结合,提出了PRRT*算法,减少了迭代次数并提高了算法的实时性.文献[12]在RRT*的基础上引入双树扩展策略,提出了RRT*—Connect算法,通过两树同时扩展提高了算法搜索速度,并在状态空间中不断寻找比当前树更好的解决方案,提高了路径质量.文献[13]将目标偏向思想引入RRT算法（Biased—RRT）,通过使采样点以一定的概率等于目标点,引导节点向目标点扩展,减小了在全局状态空间随机采样耗费的代价.该思想是一种经典的RRT改进思想,在众多RRT相关论文中都有体现,如文献[14]在节点扩展时考虑了目标偏向思想并应用于荔枝采摘机器人上.文献[15]等将回归机制引入RRT算法,防止了对配置空间的过度搜索.此外,采用自适应扩展机制,不断改善可达空间信息,避免重复搜索扩展节点,提高了路径规划效率.文献[16]等通过人工引导的方法生成随机点,获得了更高的搜索速度,且引入并改进了逆运动学算法,降低了算法的计算成本.文献[17]等提出一种基于贪婪策略的双向快速探索随机树算法,通过对节点的扩展策略进行改进,提高了求解效率,并节省了存储空间;此外,采用自适应步长滚动检测方法,提高对环境突发威胁的灵敏度.文献[18]引入了人工势场法思想,提出基于RRT的变步长搜索,通过自主地调整步长以提高搜索效率.针对规划路径不平滑的问题,文献[19]提出一种基于最大曲率约束的后处理方法用于生成光滑的可执行轨迹.文献[20]引入了强化学习思想,通过设定扩展结点的多种目标函数,以实现路径规划多目标决策优化的目的.

以上研究通过对算法步长和节点扩展策略进行优化,使得算法搜索效率得以提高.但由于其采样过程大多采用伪随机序列生成单个采样点,会使各采样点之间分布不均匀,可能导致采样点聚集,徒增采样频次.因此采样效率低,采样点质量不高是RRT算法亟待需要解决的问题.此外机械臂路径规划一般是在高维的关节空间中进行,随着维度的增加,空间复杂度也极大的提升,导致传统RRT算法效率低,而不再适用.针对上述问题,本文提出了一种基于Sobol序列[21]采样与目标偏置RRT融合的路径规划算法（Sobol—RRT）.并将Sobol—RRT与传统的RRT算法进行了对比分析,验证了Sobol—RRT规划出的路径更短,效率更高.最后以AUBO—i5机械臂为原型,在MATLAB中建立机械臂模型,验证了算法在机械臂上应用的优势.相比标准RRT 算法,本文的主要贡献在于:

1）为避免RRT全空间盲目随机采样以及采样点聚集问题,在目标偏置RRT算法基础上,引入Sobol序列采样方法,增强了目标搜索方向上的采样均匀性,有效避免了冗余、重复的采样点,提高了算法的快速性以及空间探索能力.

2）建立了基于采样池策略的采样点优选方法,其采用并发采样策略,构建采样池,从中挑选出距离目标点最近且生成节点不与障碍物交涉的采样点作为最优采样点,进一步提高了算法的搜索性能.

2 机械臂路径规划问题描述

机械臂路径规划的研究,主要是实现机械臂在障碍物环境下自主寻找出一条从给定起点到目标点的无碰撞路径.为减轻算法的计算压力,本文在关节空间中对机械臂的各关节角进行路径规划,这避免了机械臂逆运动学的求解,减轻了计算压力.本文以AUBO—i5机械臂为研究对象,该机械臂的机械结构图如图1所示.通常情况下,采用D—H法建立机械臂模型,AUBO—i5机械臂对应的D—H参数如表1e所示.通过该方法可以得出第i-1关节坐标系到第i关节坐标系的变换矩阵,进而得出基坐标变换矩阵到各个关节的坐标关系.由此可以计算出各关节末端执行器的位姿矩阵,进而执行与障碍物的碰撞检测.对于通用的六自由度机械臂而言,由于第6关节对于末端位置影响很小,因此可以将六自由度结构的机械臂进行合理简化,先规划第1—5个关节角,当前5个关节角都到达目标位置时再使第六关节角执行到目标点.

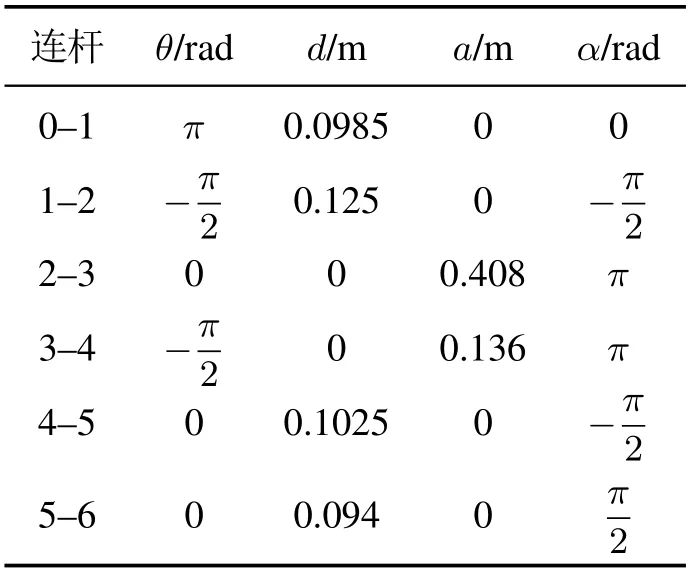
表1 机械臂D—H参数表Table 1 D—H parameter table of manipulator

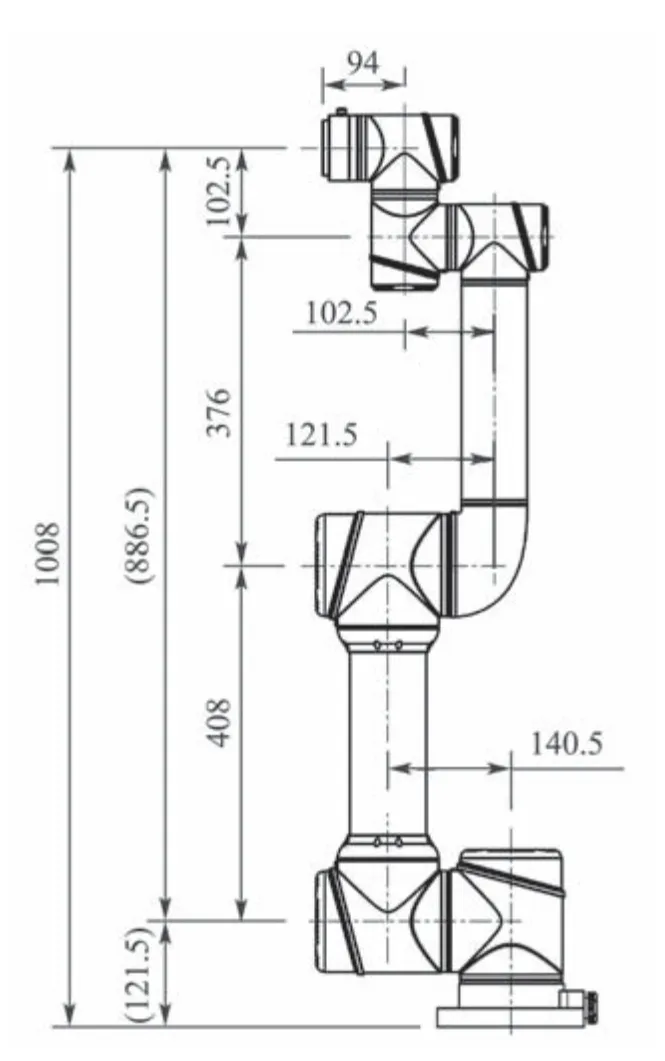
图1 机械臂机械结构图Fig.1 Mechanical structure of manipulator

由于在实际应用环境中机械臂和障碍物都是不规则的物体,很难设定它们之间的碰撞条件.因此需要将机械臂和障碍物进行简化,研究他们之间的碰撞条件,本文使用几何包络法简化机械臂与障碍物的碰撞模型[22].如图2所示,机械臂连杆由圆柱体完全包裹,障碍物可以由球体或矩形包裹,最终机械臂与障碍物的碰撞检测就变成了一系列判断规则几何体交涉的问题.该模型简化方法虽然会损失一部分机械臂运动的自由空间,但简化了碰撞模型,提高了计算效率.

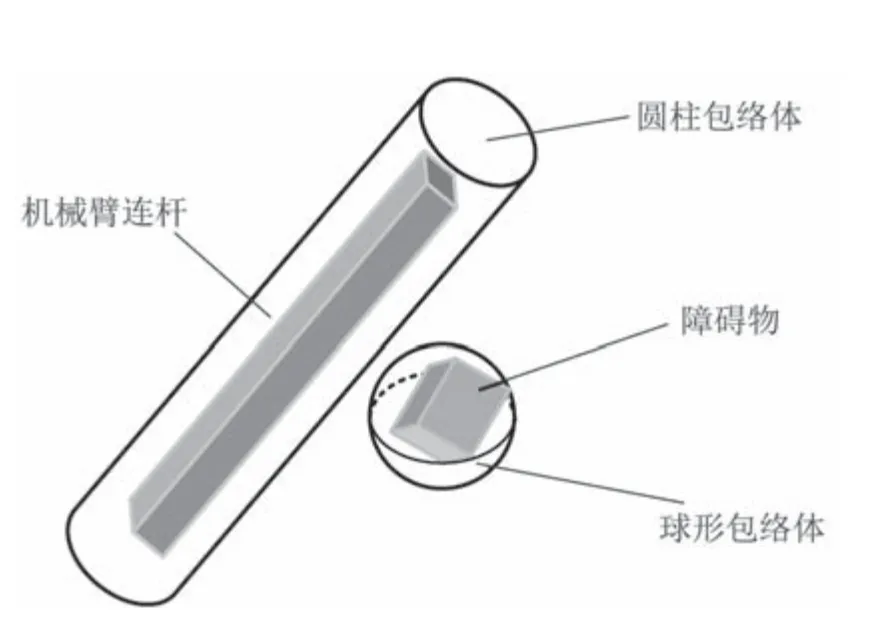
图2 模型简化示意图Fig.2 Simplified model diagram

3 路径规划算法

3.1 RRT算法基本原理

RRT是一种基于随机采样的快速搜索方法,它在进行路径搜索时,把扩展得到的随机节点存储于一个树状结构中,并继续向未知空间探索,直到接触目标点为止.

图3为标准RRT原理示意图.其中Obstacle为障碍物空间,空白区域为Cfree空间.以初始节点xinit作为树根开始扩展,黑色球体为逐步扩展增加到随机树上的节点,xnew为当前随机树扩展的新节点.新节点的扩展策略为:首先通过随机采样得到采样点xsample;然后找到随机树中离xsample最近的节点xnearest,在方向上以一定的步长step生成xnew;判断xnearest,xnew两点间连线是否与障碍物发生碰撞,若否,则将xnew加入随机树中,并定义xnearest为xnew的父节点;若类似节点1发生碰撞,则重新进行采样.接着,判断随机树是否生长至目标节点xgoal附近处,若是,则算法结束,反之,则继续生长直至到达距离目标点允许的误差范围之内;最后回溯父子关系得到规划出的路径.

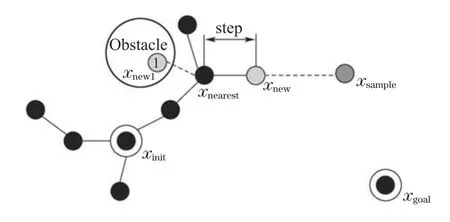
图3 标准RRT原理示意图Fig.3 Schematic diagram of standard RRT

标准RRT算法的实现过程算法1描述:给定路径起始点xinit,目标点xgoal,设置步长为step,允许误差为error,随机树上节点集合为T.

算法1标准RRT算法实现.

步骤1初始化随机树节点集合T,将初始点xinit加入T中;

步骤2在搜索空间中随机采样生成采样点xsample;

步骤3在随机树T中选择距离采样点xsample最近的点作为最近节点xnearest;

步骤4以一定的步长step在xnearest与xsample方向上扩展新节点

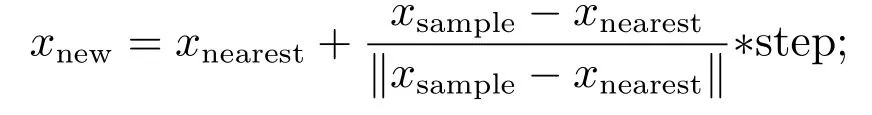
步骤5判断xnew是否与障碍物交涉,若否,将其加入随机树中且定义xnearest为xnew的父节点,若是,舍弃该节点返回步骤2重新进行本次节点扩展;

步骤6判断当前节点xnew与目标点xgoal之间的距离是否小于或等于误差error.若是,停止迭代搜索将目标点加入T中,否则,重复上述步骤直到满足条件;

步骤7回溯父子关系得到规划路径.

3.2 基于Sobol-RRT的路径规划算法

本文首先在采样过程中使用低差异的Sobol序列代替伪随机序列生成新的采样点,增强算法对未知空间的探索能力,避免采样点聚集,提高采样效率,加快算法收敛.其次将目标偏置策略引入RRT算法,使随机树以一定的概率向目标点方向生长,减小了随机的盲目性.同时在采样时建立采样池,每次选取多个采样点存入采样池中,从中挑选出距离目标点最近且生成节点不与障碍物交涉的采样点作为最优采样点,以达到对采样点进行优选的目的.

3.2.1 基于Sobol序列的采样策略

标准RRT算法的采样点是采用随机数生成算法在采样空间中随机得到的,而所有基于现代CPU的随机数生成算法都是伪随机的,会产生重复和聚集现象,造成一些无效采样.低差异序列是一种在给定空间内比伪随机序列分布更加均匀的序列,其具有这样的性质,即任意长度的子序列都能均匀的填充整个函数空间[21].图4所示为使用伪随机序列和低差异的Sobol序列在二维空间中采样得到的采样点分布对比图.其中图4（a）为使用伪随机序列生成的采样点,可以看出在该图中发生了多处采样点聚集（如实线标注）,也有一些区域未被采样到（如虚线标注）.图4（b）为使用Sobol序列生成的采样点,可以看出在该图中的任何特定区域的采样点都能够均匀分布,具有一定的均匀差异性.这种均匀差异性可以避免产生重复或相似采样点,提高采样点的分布质量,并且当RRT算法节点扩展遇到障碍物时,需要采样点之间具有的一定的差异性,使得由下一采样点生成的新节点尽可能地避开障碍物,以节省算法时间.此外Sobol序列是一组确定有序的数字排列,而节点扩展时RRT按序选取Sobol序列中相应维度的数字生成采样点,这使得每次在相同环境下使用Sobol序列采样的RRT算法,路径规划差异不大,因此具有更好的稳定性.

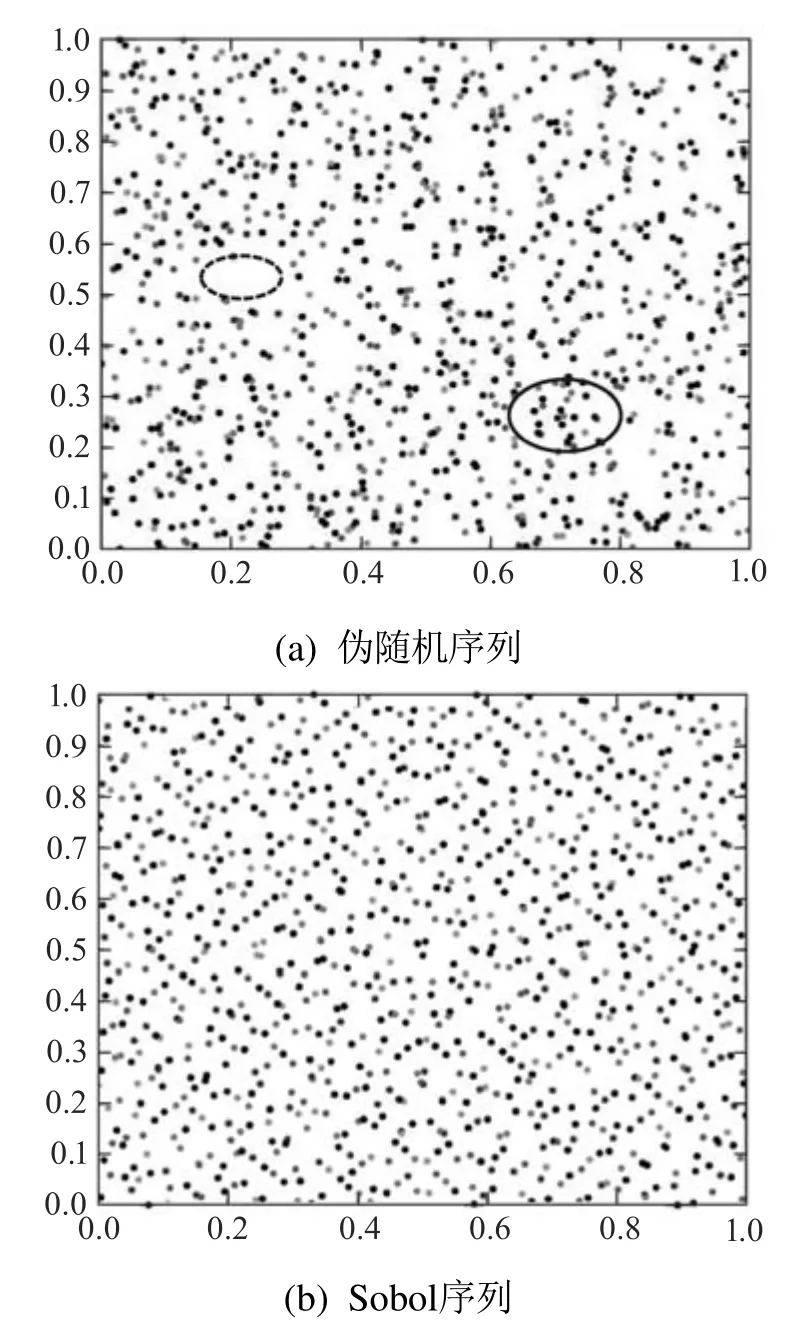
图4 采样点分布对比图Fig.4 Sampling point distribution comparison chart

低差异的Sobol序列是一组基于“方向数”vi所形成的序列（i=1,2,3,···,表示“方向数”的序号）,vi满足vi=其中mi为小于2i的正奇数,其生成依赖于如下简单多项式:

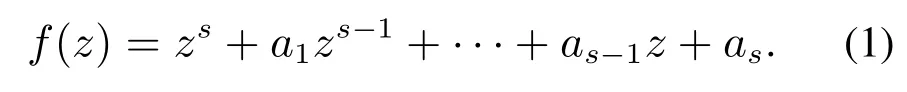
当i ＜s时需要指定mi的值,而当i ＞s时,mi递推式为

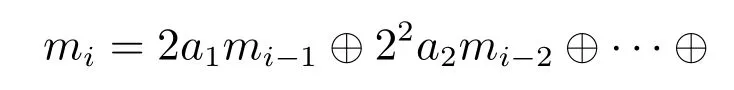
其中:···b3b2b1是i的二进制表示,⊕表示二进制按位异或,表示向下取整.上述所需的参数s,mi,a可以由生成矩阵C得到,C=(d,s,a,mi),其中d表示C的维度.Sobol序列的每一个维度都有不同的生成矩阵C,通过改变生成矩阵C可以得到不同维度的Sobol序列.目前经过Joe S和Kuo F Y等[23—24]学者的研究,可以找到最高为21201维度的生成矩阵C,用于生成高质量分布的Sobol序列.但实际应用中,考虑到时间效率和程序存储空间等因素,本文使用5000维的生成矩阵C,这远远能够满足RRT算法的采样次数需求.

3.2.2 目标偏置策略

针对RRT算法的盲目性问题,引入文献[14]提到的目标偏置采样策略,该方法的核心思想是在随机树生长过程中以p为目标偏置概率使得xsample=xgoal,以(1-p)的概率随机采样获得xsample.该方法使得算法在节点扩展时具有一定的目标导向性,平衡了算法对未知空间的探索能力和算法运行的时间.p值的选取影响着搜索过程和搜索结果,一般规律为,当环境障碍物密集时应使p值较小,保持算法对未知空间的探索能力,反之应使p值较大,使节点以较大的概率向着目标点扩展,以节省算法时间.以图5为例,图5（a）为标准RRT在二维空间中的扩展过程,图5（b）所示为二维空间中加入目标偏置策略的RRT算法（Biased—RRT）.可以看出相较于图5（a）,图5（b）中树枝明显更少,节点扩展中减少了不必要区域的搜索,路径搜索时具有更好的目标性,因而提高了搜索效率使得收敛速度变快.

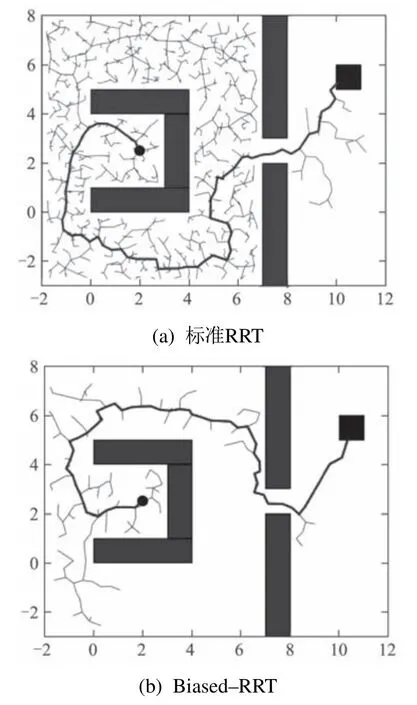
图5 标准RRT与Biased—RRT仿真对比图Fig.5 Simulation comparison between standard RRT and Biased—RRT

3.2.3 基于采样池策略的采样点优选

为了对采样点进行优选,在采样过程中建立采样池.即每次采样时选取多组采样点放入采样池中,定义采样池中距离目标点最近且生成的节点不与障碍物交涉的采样点作为最优采样点.建立采样池后的RRT算法示意图如图6所示,黑色球为已加入随机树的节点,xsample1,xsample2,···,xsampleN为本次节点扩展时采样池中的采样点.图中按采样点与目标点的欧式距离大小对采样池中的采样点从小到大进行排序,xsample1＜xsample2＜···＜xsampleN.优先选取距离目标点最近的采样点,但由xsample1生成的节点xnew1与障碍物交涉因此不可用,接着按序选取采样池中的下一采样点xsample2生成新节点xnew2,xnew2不与障碍物交涉,因此可将xsample2作为本次采样的最优采样点.若当前采样池中没有满足要求的采样点,则重新采样填充采样池.按此方法每次选取采样过程中的最优采样点,用于生成新节点加入随机树中,直到新节点到达目标点附近.

图6 建立采样池的RRT算法示意图Fig.6 Schematic diagram of RRT algorithm with sampling pool

在不同的环境中采样池容量n的大小也会影响最优采样点的选取,n值过小时,对新节点的扩展达不到较好的目标牵引性,从而导致对无效区域的过多搜索;而当n值较大时,目标性太强,当遇到凹形障碍物或其它复杂障碍物时,为求得最优采样点会增加碰撞检测次数,这消耗了路径规划时间.因此对于障碍物相对简单的环境,n值应适当取大增强目标牵引性,反之则应适当取小,增强避障能力.在同一幅地图中,使n取5,10,15,20,25,30分别进行20次实验,得到结果如表2所示.可以看出,在该地图中采样池容量最优设置范围为10～20,经过多次实验得到使平均时间最少的最优采样池容量值为18,此时平均时间为3.58 s,平均路径长度为26.17 m,平均节点数为356个,其规划出的路径如图7所示.需要说明的是在下文实验部分进行的对比实验中,本文所提Sobol—RRT算法都是在最优采样池容量值下进行的.

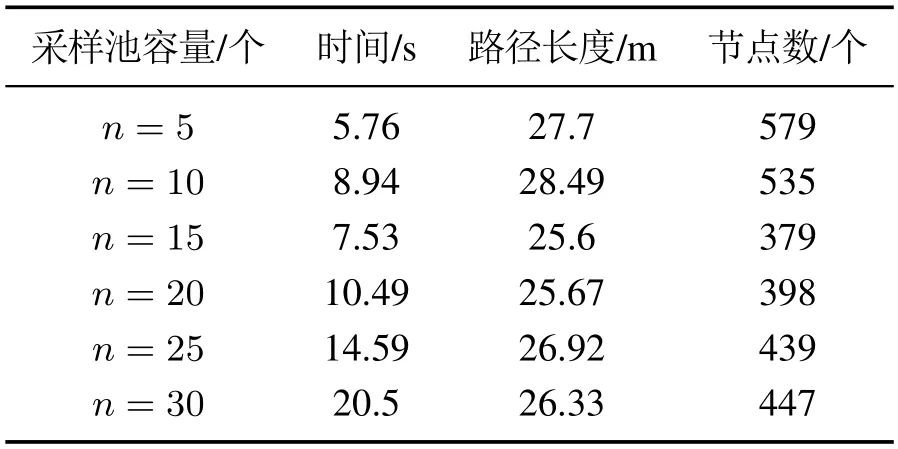
表2 采样池容量值最优设置实验结果Table 2 Experimental results of optimal setting of sampling pool capacity value

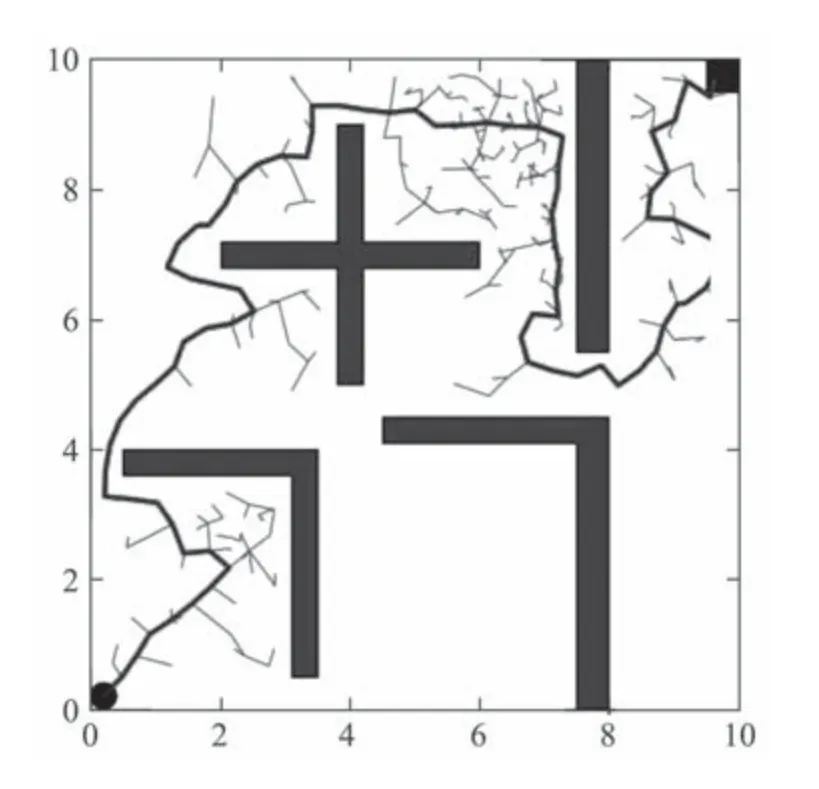
图7 采样池容量最优值设置结果图Fig.7 Result of setting the optimal value of the sampling pool capacity

3.2.4 算法实现

Sobol—RRT算法的一般实现步骤如算法2描述:给定路径起始点xinit,目标点xgoal,设置步长为step,偏置概率为p,允许误差为error,采样池中采样点个数为n,随机树上节点集合为T.

算法2Sobol—RRT算法实现.

步骤1初始化随机树节点集合T,将初始点xinit加入T中.

步骤2在区间范围(0,1)之间生成一个随机数rand比较该随机数与偏置概率p的大小.

当rand≤p时,

1）令采样点xsample=xgoal;

2）在随机树T中选择距离采样点xsample最近的点作为最近节点xnearest;

3）以一定的步长step在xnearest与xsample连线方向上扩展新节点

4）判断xnew是否与障碍物交涉,若否,将xnew加入T中且定义xnearest为xnew的父节点,否则,舍弃该节点.

当rand＞p时,

1）使用Sobol序列生成n个具有均匀差异特性的采样点按与目标点距离的远近,从小到大排列放入采样池;

2）令采样点xsample等于采样池中第1个采样点,在随机树T中选择距离xsample最近的点作为最近节点xnearest;

3）以一定的步长step在xnearest与xsample连线方向上扩展新节点

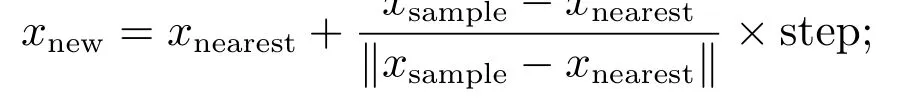
4）判断新节点是否与障碍物交涉,若否,将xnew加入随机树T中且定义xnearest为xnew的父节点,否则,舍弃该节点,按顺序选取采样池中的下一个采样点用于生成xnew,直到生成不与障碍物交涉的xnew,若当前采样池中采样点都不满足,则重新进行采样填充采样池,并重复上述步骤.

步骤3判断xnew与xgoal之间的距离是否小于等于误差error.若是,停止搜索将目标点加入T中,否则,重复上述步骤直到满足条件.

步骤4回溯父子关系得到规划路径.

以上为Sobol—RRT算法的一般实现方法,而在机械臂上应用时,由于算法是在关节空间中进行的路径规划,而障碍物是处于笛卡尔空间内,因此需要通过正运动学实现新节点由关节空间向笛卡尔空间的转换,进而得到机械臂的位姿,再与障碍物进行碰撞检测.因此Sobol—RRT算法在机械臂上的实现步骤如下.

步骤1初始化随机树数据集合,确定初始关节角度xinit和目标关节角度xgoal,把xinit加入随机树中;

步骤2以目标偏置策略采集样本,以概率p使采样点xsample等于目标节点xgoal,以概率(1-p)通过Sobol序列产生n组采样点并放入采样池中,选取离目标点最近且满足3）的采样点;

步骤3搜索随机树中与xsample距离最近的点作为最近节点xnearest,在---------→xnearestxsample方向上以一定步长生成新节点,利用正向运动学计算机械臂连杆位姿并进行碰撞检测,若未碰撞,把xnew加入树中,否则,返回2）重新采样;

步骤4判断xnew与xgoal的距离,若小于误差允许范围error,则认为随机树已经扩展至xgoal,把xgoal加入树中,回溯父子节点关系,返回随机树和规划路径,否则转到2）,树继续生长.

3.2.5 路径优化

RRT搜索得到的路径是由一些离散点组成的连续线段,路径的形状是锯齿状的,并不平滑.这不仅降低了机械臂运动的平稳性,而且会引起电机的冲击和振动,加速机械零件的磨损.因此有必要对RRT算法规划出的路径进行平滑处理,这样才能保证机械臂平稳地运动.本文采用基于最小二乘法的五次多项式拟合出光滑曲线.最小二乘法的原理是通过最小化误差的平方和寻找数据的最佳函数匹配.该方法并不要求拟合出的曲线完全经过所有的点,而是找到一条曲线使得各点到这条曲线的距离之和最小.其推导过程如下.

给定离散点(x1,y1),(x2,y2),(x3,y3),···,(xn,yn)求多项式:

的表达式,并使得

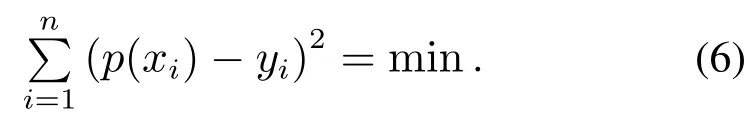
为了求得多项式（5）的系数值,对等式（6）求关于ai(i=0,1,2,···,n)的偏导,可以得到k+1个等式,如式（7）所示:

整理可得

为了便于求解,将等式（8）转换成矩阵形式可以得到

将离散点代入等式（9）中即可求出a,进而得到多项式p(x)的表达式.

本文是在关节空间中进行的关节角度路径规划,因此是对机械臂各关节角度的离散点进行拟合.图8（a）为各关节角离散点连接起来的曲线,图8（b）为使用基于最小二乘法的五次多项式拟合方法拟合出的曲线.可以看出图8（b）中关节角度曲线明显更加平滑.

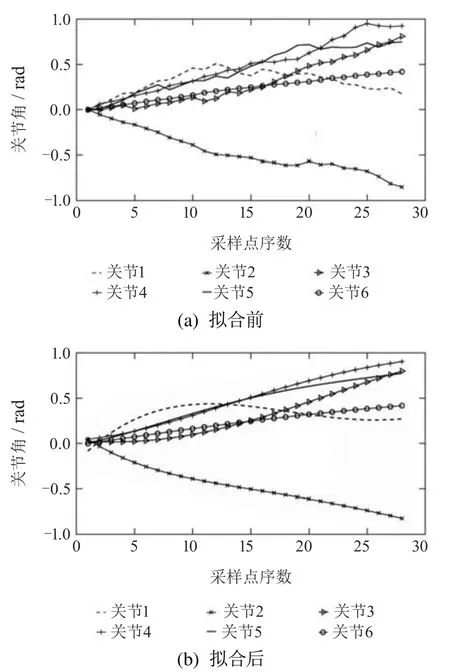
图8 基于最小二乘法多项式拟合的关节角对比图Fig.8 Comparison graph of joint angle based on least squares polynomial fitting

4 算法验证实验

4.1 二维空间下复杂路径仿真

本文首先在二维空间下选择两幅复杂度较高且具有代表性的地图进行测试,地图范围为10×10,采样点不能超过地图范围,因此横向和纵向的采样范围都是[0,10].地图中的条框为模拟的障碍物,起点坐标（1,1）,目标坐标（8.7,8.7）.其中经过多次实验设置环境1—2下目标偏置概率最优值分别为0.3和0.5;采样池容量最优值分别为12和13.并在此参数下对Sobol—RRT与Biased—RRT和标准RRT均做了20次实验,得到了不同规划时间的结果,图9—10给出的是平均时间下的一次实验结果.通过3种算法在不同地图中的对比,可以看出Sobol—RRT算法在两个复杂环境中规划出的路径长度更短,同时减少了无效区域搜索,节省了搜索时间,使得搜索更加高效,目的性更强.

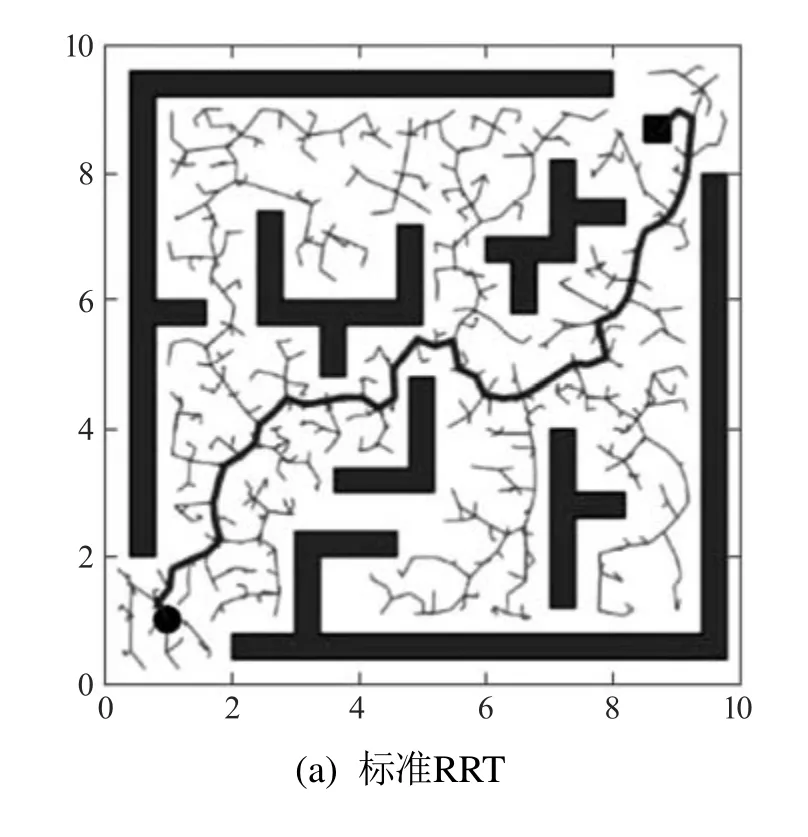
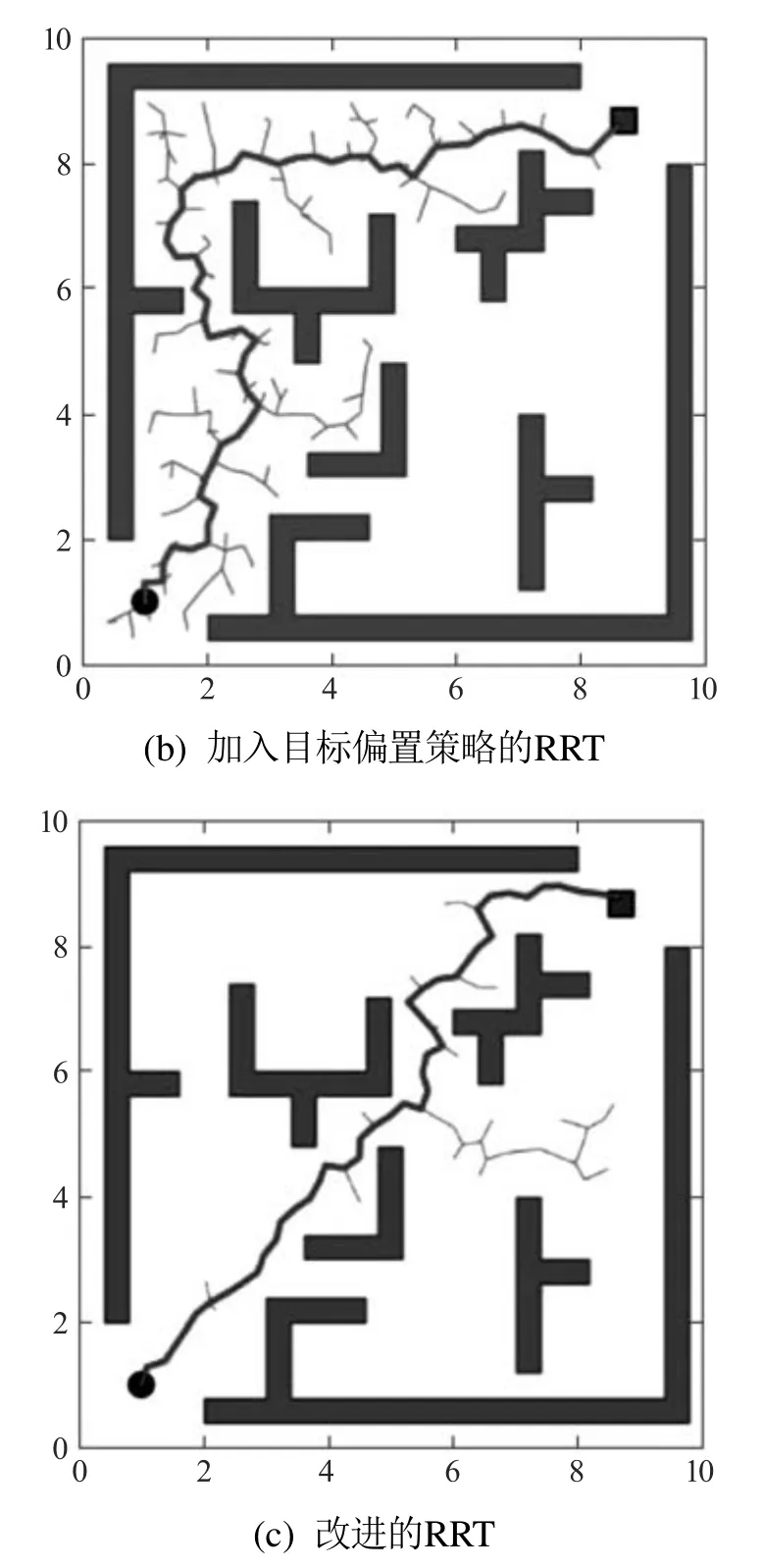
图9 测试环境1下3种算法对比图Fig.9 Comparison of three algorithms in test environment 1

为了客观评价3种RRT算法,将20次实验结果进行统计分析.需要说明的是本文所有的仿真实验都是在配置为:AMD Ryzen 5 4600U with Radeon Graphics 2.1 GHz,RAM 16 GB的计算机中完成的.

图11为3种算法路径长度对比图,从图中可以看出Sobol—RRT算法路径长度比其它两种算法路径普遍要短,且稳定性更高.

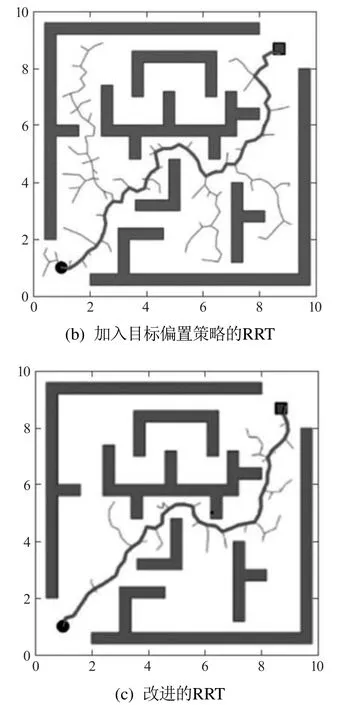
图10 测试环境2下3种算法对比图Fig.10 Comparison of three algorithms in test environment 2

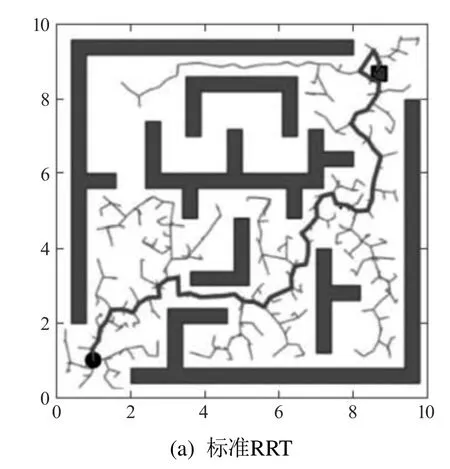
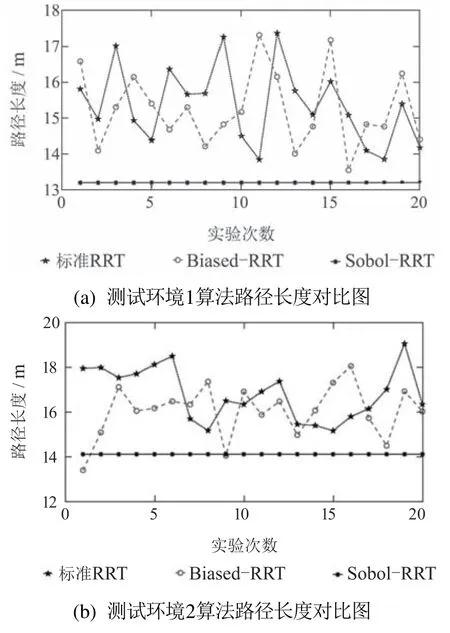
图11 算法路径长度对比图Fig.11 Path length comparison chart

如表3所示,测试环境1中,标准RRT算法路径平均长度为15.363 m,Biased—RRT算法路径平均长度为15.245 m,Sobol—RRT算法路径平均长度为13.196 m.Sobol—RRT路径长度相比较标准RRT缩短了14.11%,较Biased—RRT缩短了13.44%.测试环境2中,标准RRT算法路径平均长度为16.822 m,Biased—RRT算法路径平均长度为16.055 m,Sobol—RRT 算法路径平均长度为14.119 m.相比较标准RRT,Sobol—RRT路径长度缩短了16.07%,较Biased—RRT缩短了12.06%.通过以上数据可看出两种环境下Sobol—RRT路径长度比其它两种算法都缩短了14%左右.且两种环境下路径长度的方差Sobol—RRT＜Biased-RRT＜标准RRT,因此从路径长度上看Sobol—RRT算法规划的路径更短,且稳定性更高.图12为3种算法的时间对比图,从图中可以看出Sobol—RRT相比于其它两种算法,时间都有大幅度减少,且每次数据浮动不大.如表3所示,测试环境1中标准RRT20次实验时间平均值为1.188 s,Biased—RRT平均值为0.744 s,Sobol—RRT平均值为0.233 s.Sobol—RRT相较于标准RRT时间减少了80.39%,较Biased—RRT减少了68.68%.测试环境2中标准RRT的20次实验时间平均值为0.874 s,Biased—RRT平均值为0.799 s,Sobol—RRT平均值为0.256 s.Sobol—RRT相较于标准RRT时间减少了70.71%,较Biased—RRT减少了67.96%.通过数据可以看出,两种环境下Sobol—RRT相比于其它两种RRT算法,时间缩短都在70%左右.且在两种环境下,时间方差Sobol—RRT＜Biased—RRT＜标准RRT,因此从算法时间上分析,Sobol—RRT算法不仅效率更高,而且稳定性更好.

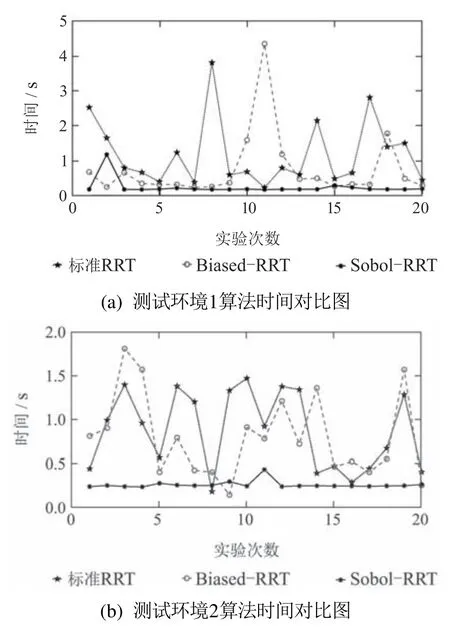
图12 算法时间对比图Fig.12 Time comparison chart

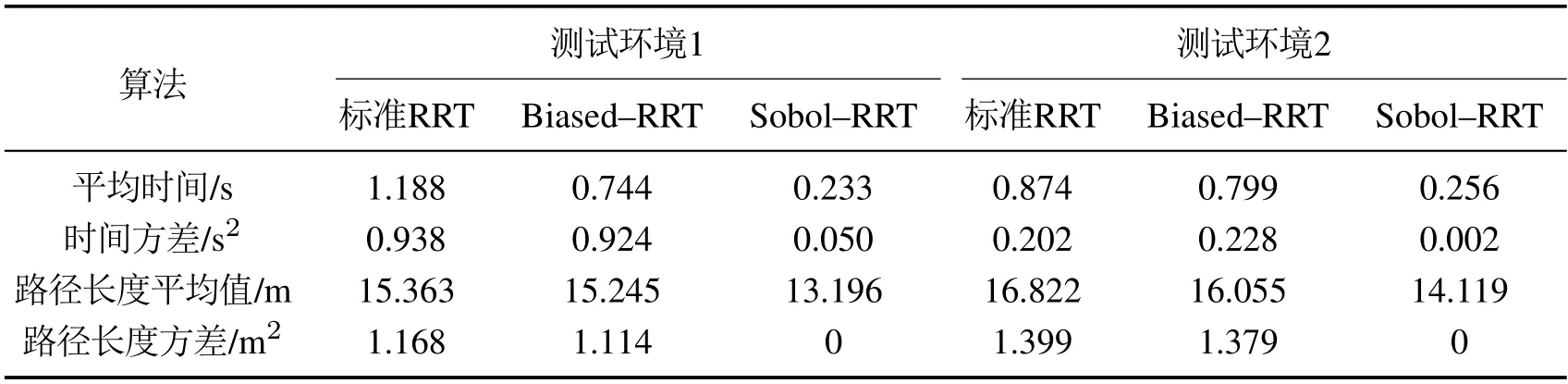
表3 数值仿真结果对比Table 3 Comparison of simulation results

以上实验结果可以看出,通过使用Sobol序列代替伪随机序列优化了采样点的分布情况,使得相邻维度的Sobol数具有一定的差异性.因此当扩展节点遇到障碍物时,能够通过采样点之间的差异性,使得生成的新节点尽快避开障碍物.且Sobol序列是一组确定有序的序列,每次实验时可按序选取相应维度的Sobol数生成采样点,因此在同一环境下每次规划出的路径基本相同,这使得算法具有更好的稳定性.其次建立采样池策略,即每次采样时选取多组采样点放入采样池中,定义采样池中距离目标点最近且生成的节点不与障碍物交涉的采样点作为最优采样点.通过对采样点的优选能够在保证算法搜索性能的前提下,使得新生成的节点距离目标点更近从而逐步缩短路径,并减少对无效区域的搜索以达到一个渐进优化的效果.为了进一步缩短搜索时间,本文又引入了用于RRT的经典改进策略—目标偏置策略,通过使采样点以一定的概率p等于目标点,以(1-p)的概率使用Sobol序列采样,使得RRT算法在保证概率完备性的前提下,引导着节点向目标点扩展以提高算法的收敛速度.

4.2 机械臂路径规划应用研究

4.2.1 三维仿真实验研究

由于仿真环境更加灵活,障碍物和实验任务更容易设置,更方便检验算法的性能,因此首先在MATLAB环境中搭建仿真环境并进行算法对比实验.如图13所示为搭建的机械臂仿真模型,球形物体为模拟出的障碍物,机械臂初始关节角为（0,0,0,0,0,0）,目标关节角为机械臂所要完成的任务为从初始关节角到目标关节角规划出一条无碰撞的路径,也即机械臂由图13（a）所示的初始位姿变换成图13（b）的目标位姿.

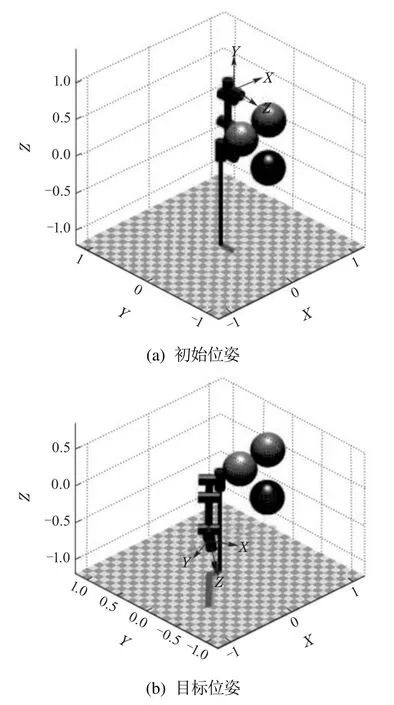
图13 机械臂仿真模型Fig.13 Simulation model of the manipulator

由于所研究的六自由度机械臂中,对末端定位起主要作用的是第1—5个关节,因此采样函数只需要对前5个关节角度进行采样.关节角采样点由式（4）的x1-x5组成,使用不同矩阵C可以得到不同维度的Sobol序列,假设使用维度为d的矩阵C,那么采样点可以由式（10）得到

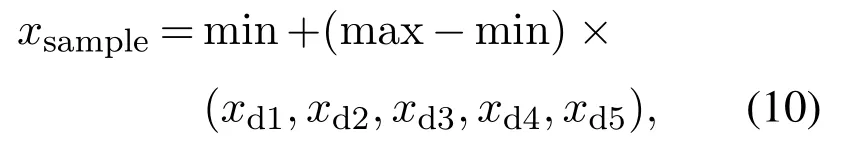
其中max,min表示采样点上下限,这里表示AUBO—i5机械臂的1—5关节角限制,关节角限制大小与机械臂本身的结构有关.由于AUBO—i5机械臂的每个关节角都可以进行的旋转,因此

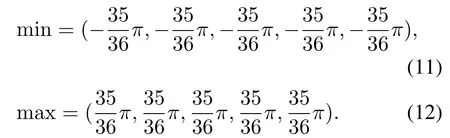
为了说明本文所提Sobol序列采样和采样池优选策略的有效性,将Sobol—RRT与RRT—Connect,RRT*以及RRT—BCR[15]3种算法进行对比.同时为了排除目标偏置策略对Sobol—RRT带来的性能提升因素,实验中给进行对比的另外3种算法都加上目标偏置策略.经过多次实验,设置能使3种算法综合性能最优的目标偏置概率值为0.5,并设置Sobol—RRT 算法中采样池容量最优值为12.图14—17为选取4种算法20次实验中,搜索时间等于平均时间的一次实验结果.其中图（a）为机械臂路径规划过程中关节角度映射到机械臂末端的路径搜索示意图;图（b）为各关节在笛卡尔空间的位置图,由于第1个关节位置是固定不变的,因此只展示了第2—6个关节;图（c）为模拟环境下机械臂根据规划出的路径运动示意图.

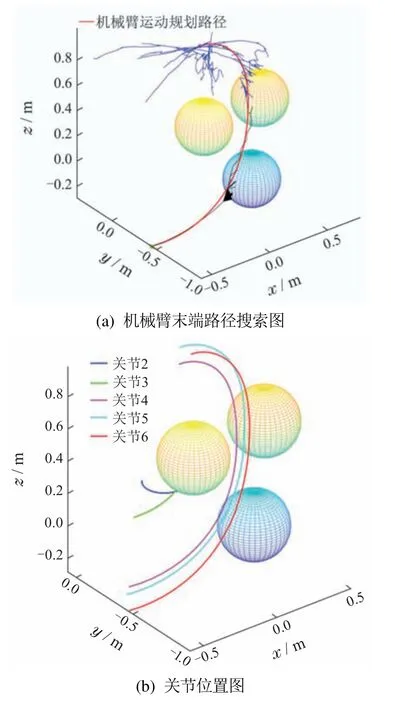
图14 RRT—Connect实验结果示意图Fig.14 Schematic diagram of RRT—Connect experimental results

结合图18和表4的20次实验结果可知,Sobol—RRT在整体实验数据上都优于RRT—Connect和RRT*.这是由于Sobol—RRT加入了采样池优选策略和Sobol序列采样的方法.采样池优选策略的核心是一次选取多个采样点放入采样池中,并选取距离目标点最近且生成的新节点不与障碍物交涉的采样点作为采样池中的最优采样点,该策略使得Sobol—RRT在无障碍区域能够尽可能避开对无效区域的搜索,而在障碍物区域能够利用Sobol序列生成采样点之间的均匀差异性,避免相似或重复采样,使机械臂能够尽快离开障碍物.而图14中的RRT—Connect虽然由两棵树同时搜索,但由于树2的采样点取决于树1的新节点,因此扩展方向受限.在机械臂高维的关节空间中一旦树2扩展时遇到障碍物就很难跳出当前状态,使得搜索时间变长.如图15所示,RRT*算法是一种路径长度渐进最优的算法,每次扩展时,选取新节点附近的节点中与起始点之间路径最短的点作为父节点,由于每次扩展新节点都要计算之前路径长度,虽然能使路径长度渐进最优,但无疑增加了计算压力,因此规划时间也更长.

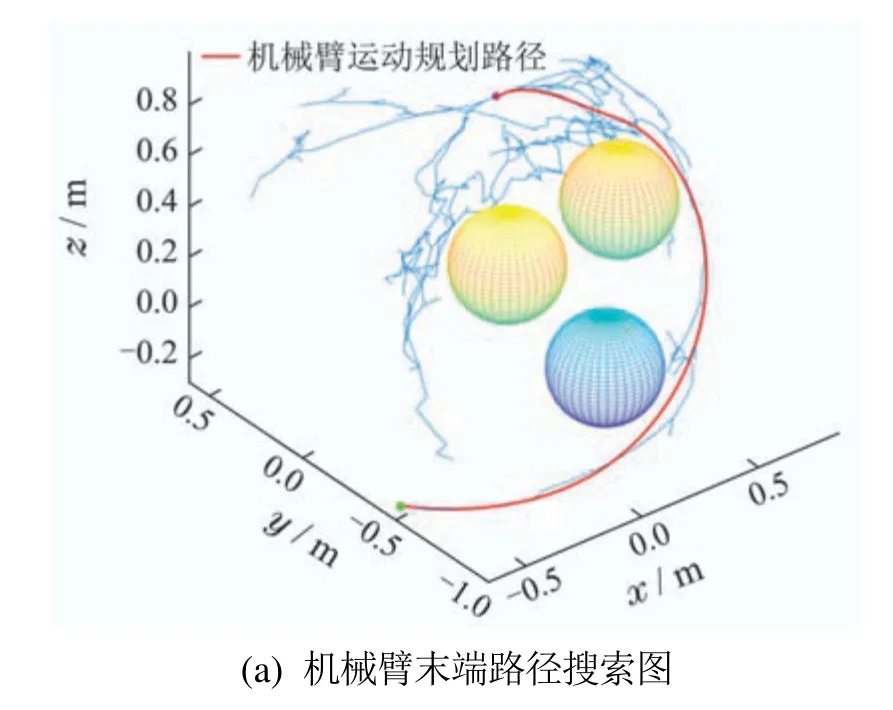
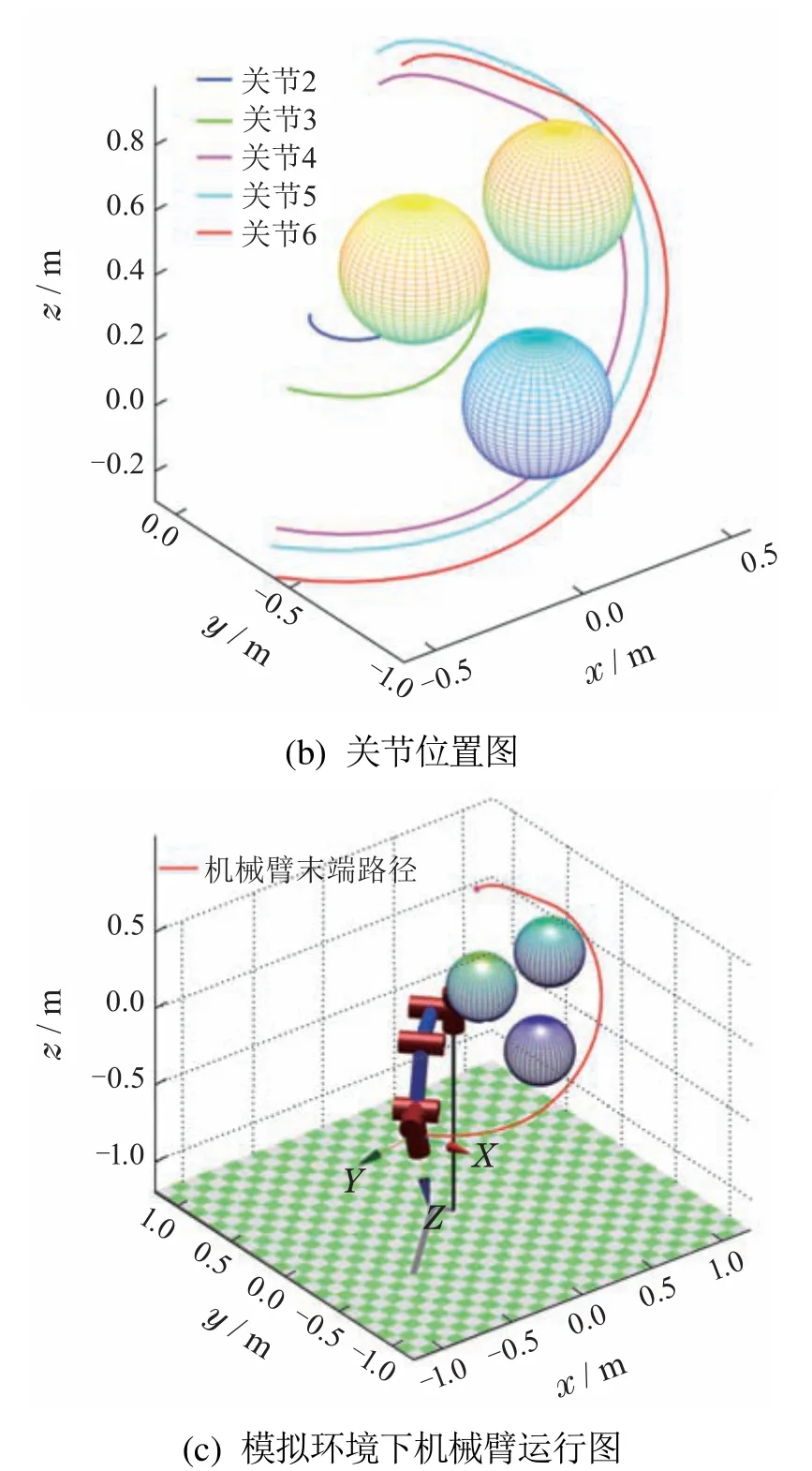
图15 RRT*实验结果示意图Fig.15 Schematic diagram of RRT*experimental results

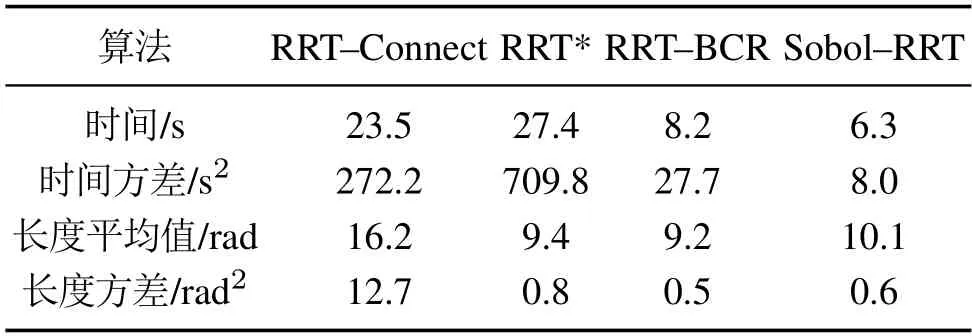
表4 实验数据统计表Table 4 Experimental data statistics table

如图16所示,RRT—BCR算法通过将回归机制引入RRT算法,防止了对配置空间的过度搜索.此外,采用自适应扩展机制,通过细化边界节点,不断改善可达空间信息,避免了对同一节点的重复搜索,因此减少了节点扩展时的碰撞检测次数,也消除了大部分冗余节点.

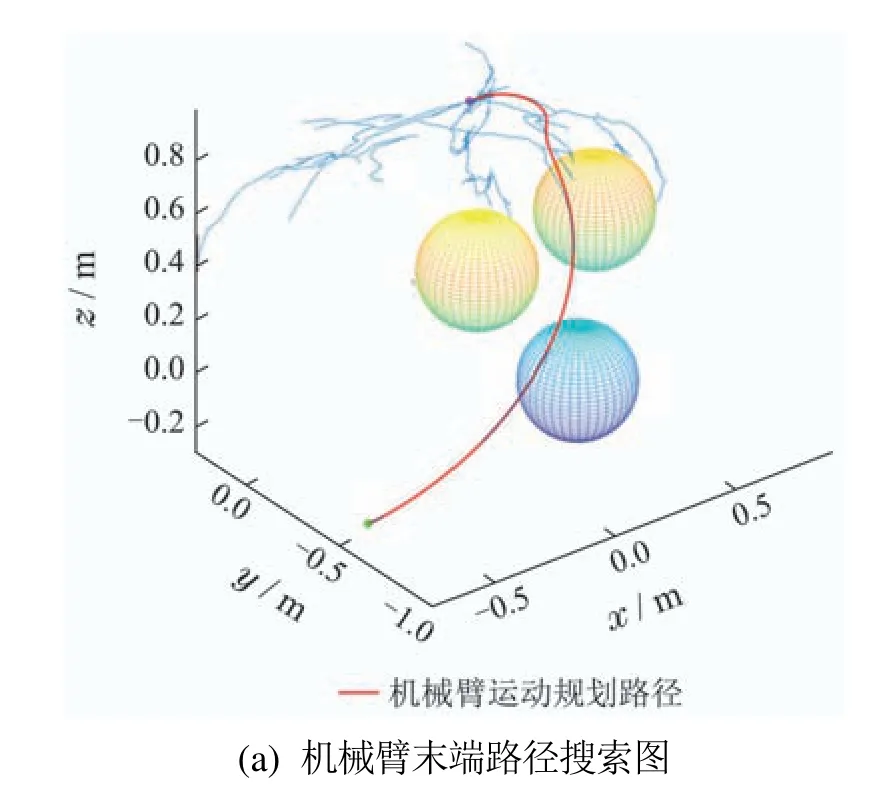
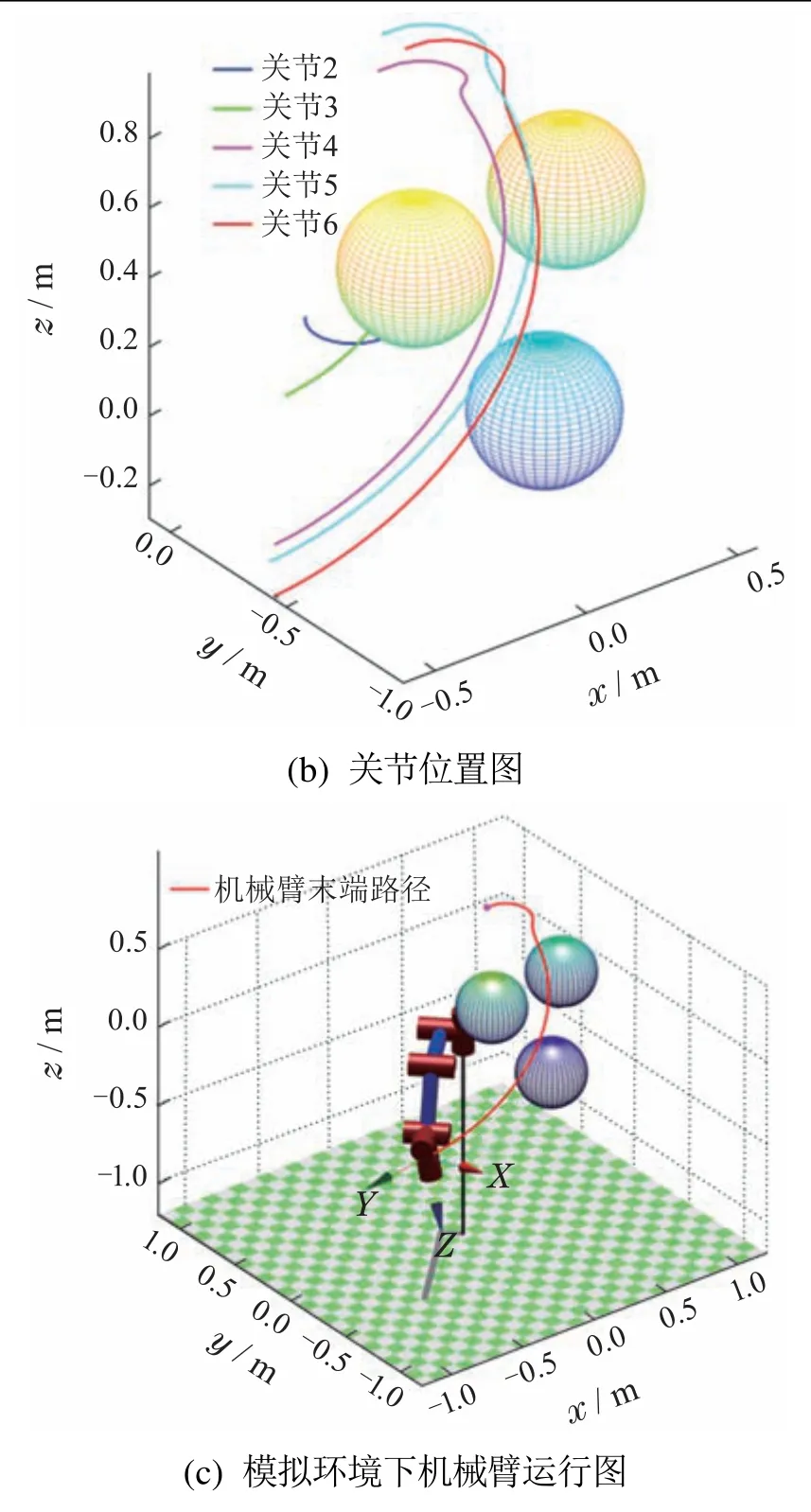
图16 RRT—BCR实验结果示意图Fig.16 Schematic diagram of RRT—BCR experiment results

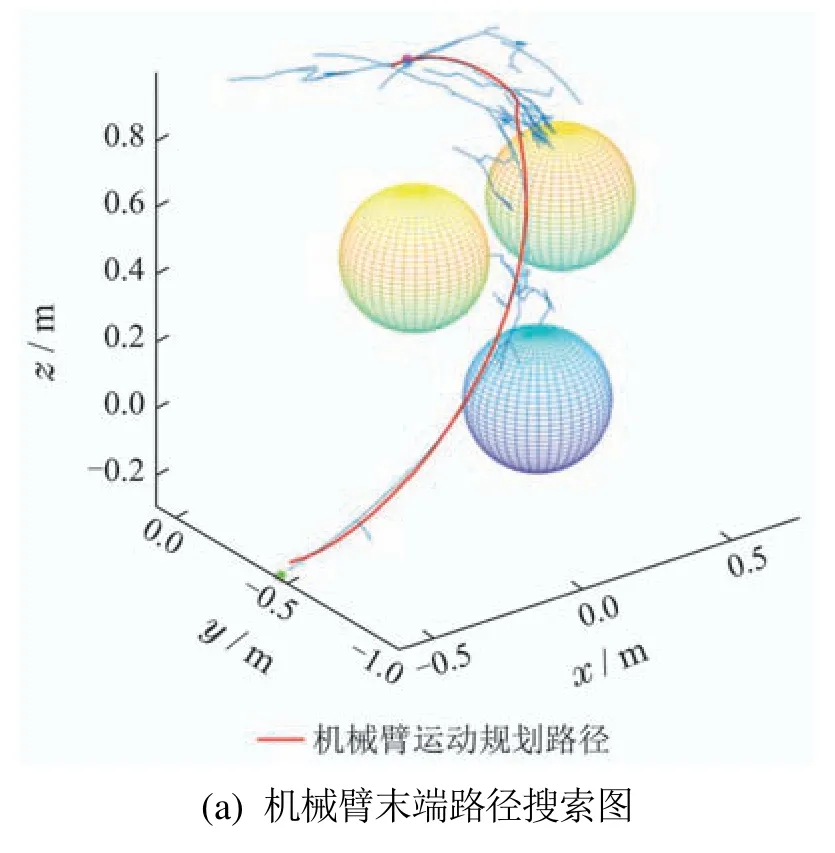
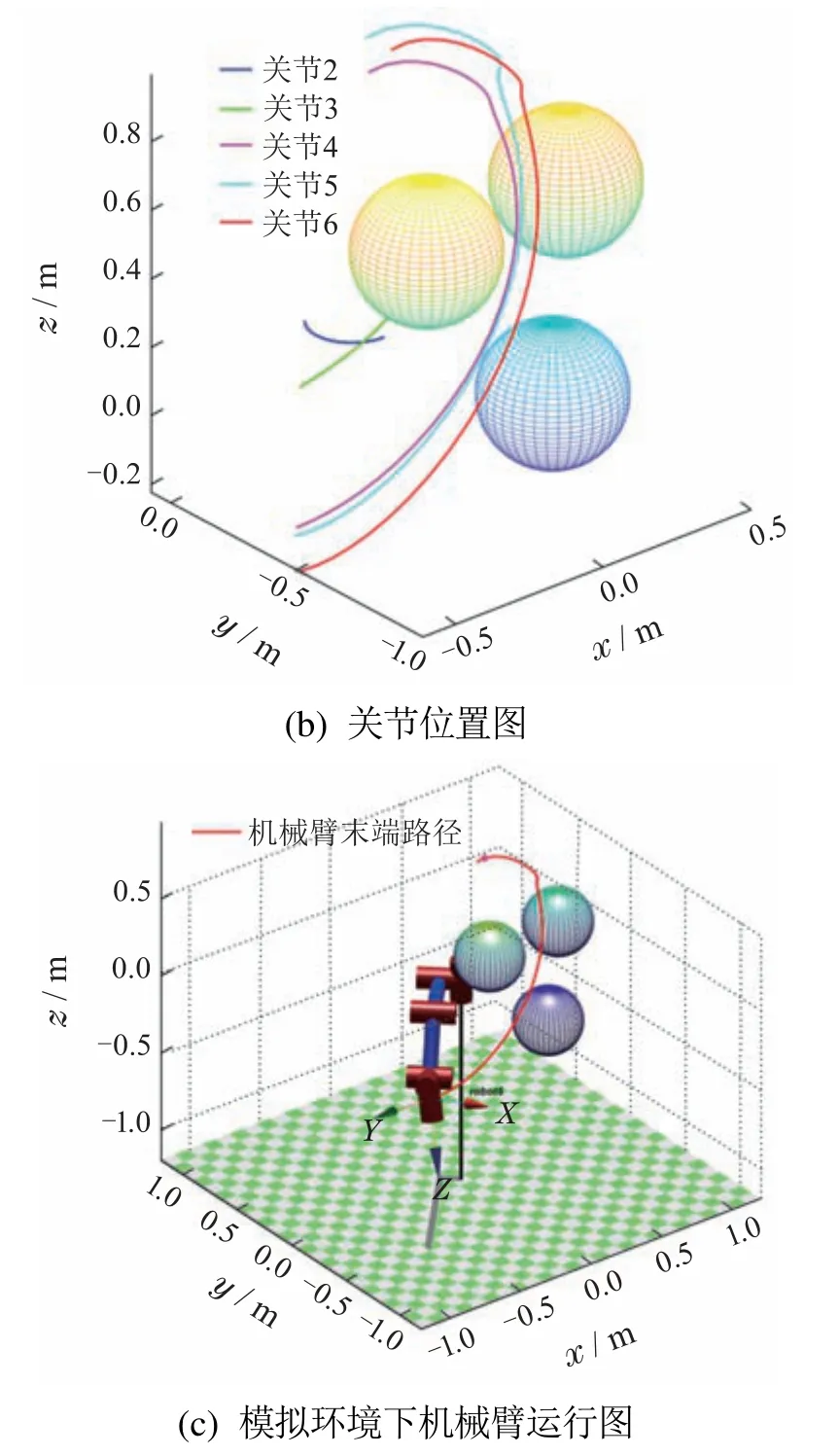
图17 Sobol—RRT实验结果示意图Fig.17 Schematic diagram of Sobol—RRT experiment results

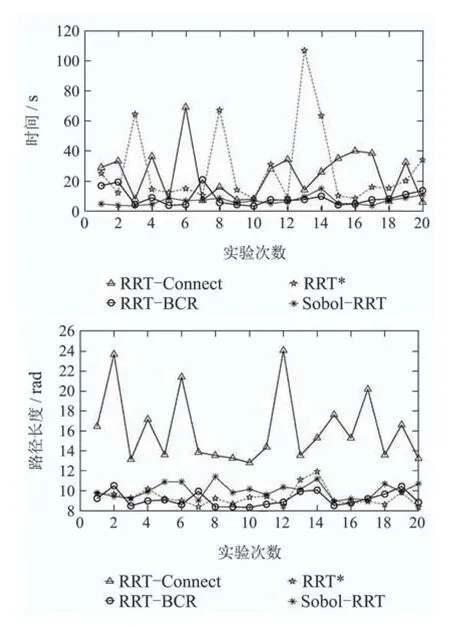
图18 实验数据统计示意图Fig.18 Schematic diagram of experimental data statistics

由于节点数变少,所以通过连接每个节点生成的路径,其冗余度也会降低,这使得路径长度更短.通过减少碰撞检测次数,使机械臂正运动学计算次数也相应的减少,这提高了算法的计算效率,节省了路径规划时间,但从时间上来看,相比于RRT—BCR,本文所提Sobol—RRT算法优势更为明显.

4.2.2 实物实验

为验证文中所提Sobol—RRT算法的可行性,本文搭建了如图19所示的机械臂实验平台.硬件设备采用遨博公司的AUBO—i5机械臂及其配套的控制箱,为了更加直观的显示机械臂运动轨迹,利用Modbus Slave软件搭建从站,将其对接到控制箱自带Modbus Tcp主站,其机械臂关节控制量和机械臂末端位置信息存放到此数据空间,并将子站挂载到OPC服务器作为数据共享源,MATLAB轨迹控制算法能够以此实时控制机械臂运作,而基于Unity3D的虚拟现实场景能够通过该数据共享源,同步虚拟机械臂运作并绘制运动轨迹.机械臂的起始关节角和目标关节角分别为

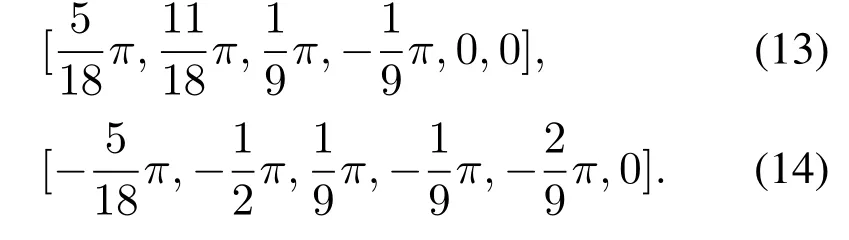
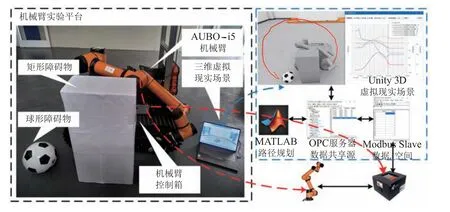
图19 机械臂实验平台Fig.19 Manipulator experiment platform

图20（a）为机械臂运行过程中末端关节位置变化图,图20（b）为仿真路径规划过程中的关节角变化曲线,图20（c）为实物实验中AUBO—i5机械臂反馈的关节角变化曲线.从图20（a）中可以看出机械臂首先从初始位姿到达球形障碍物附近,当检测到障碍物时运动轨迹发生变化开始向上运行,在运动中间过程中由于机械臂其它关节位置也会与障碍物进行碰撞检测,因此最终搜索到一条较大轮廓的轨迹.相比于图20（b）而言,图20（c）的关节轨迹呈现一定的锯齿状,这是由于实际运行过程中具有一定的噪声,且控制指令的更新频率也会对结果造成轻微影响,但从实际运行情况来看,在可允许的范围之内.总体来看,在避障过程中,机械臂运行过程中较为平稳,关节角度无突然变化,因此可以证明所提算法在AUBO—i5机械臂实物上应用的可行性.

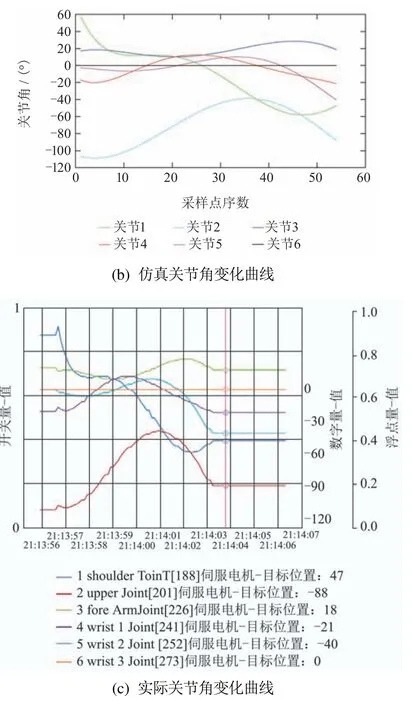
图20 实验结果Fig.20 Experimental results

5 结论与展望

本文结合了Biased—RRT的优点对RRT算法加以改进,引入Sobol序列采样与采样池优选策略的思想,提出了Sobol—RRT算法.并首先在两种复杂的二维环境中对3种RRT进行仿真,结果表明Sobol—RRT可以有效的避开障碍物且效率高、稳定性好、路径短;接着在MATLAB中进行了Sobol—RRT与同样加入目标策略的RRT—Connect,RRT*和RRT—BCR算法的3维仿真对比实验,证明了相比于其它改进的RRT,Sobol—RRT在机械臂路径规划上应用的优势;最后搭建了机械臂实物实验平台,并将Sobol—RRT用于实物机械臂AUBO—i5上,结果表明,机械臂可以平滑稳定地避开障碍物到达目标点,证明了所提算法在机械臂上应用的有效性.

未来的研究重点将主要考虑将所提算法用于矿用废弃地土壤采样机器人进行土壤抓取实验,并根据实际应用需求设计相应的实验场景,以检测该算法存在的问题,便于下一步提出改进策略.此外Sobol—RRT是一种通用型算法,不仅适用于机械臂路径规划,也可以应用在于无人机,智能车等场景中.下一步也考虑提升该算法的泛化能力,将其应用于土壤采样机器人移动底盘部分的路径规划.