基于强化学习的一类具有输入约束非线性系统最优控制

罗 傲,肖文彬,周 琪,鲁仁全

（广东工业大学广东省智能决策与协同控制重点实验室,广东广州 510006）

1 引言

随着世界能源危机的日益严峻,最优控制已经成为实际生产生活中一项重要设计方案[1—3].对于被控对象效用函数为二次型的线性系统主要通过求解黎卡提（Riccati）方程获得其最优解.然而,实际中大部分被控系统具有复杂非线性的特点,需要求解哈密顿—雅可比—贝尔曼（Hamilton—Jacobi—Bellman,HJB）方程.由于HJB方程具有强非线性,从而导致难以获得方程解析解,同时,随着系统维数的增加,求解过程中会产生“维数灾”问题.因此,如何通过近似算法获得HJB方程解,是当前优化控制领域研究的热点问题[4—6].近年来,基于强化学习执行—评价网络的自适应评判控制策略被广泛应用于非线性系统的最优控制问题.该方法利用神经网络或模糊逻辑系统的近似特性得到HJB方程解,为非线性系统的最优控制问题的求解提供了新途径[7—11].

反步法作为一种系统化的控制设计方法,具有结构简单,鲁棒性强的优势,能有效解决复杂非线性系统控制问题,极大地促进了非线性系统控制理论的研究[12—27].综合反步法在解决n阶不确定非线性系统跟踪问题上的优势,许多专家学者尝试将强化学习与反步法相结合并提出了相应的控制算法[28—32].其中,文献[28—29]为实现跟踪控制,将控制器设计分为两个部分:基于反步法的前馈控制器和基于强化学习的最优控制器,但该方法无法保证所有虚拟控制器为最优,并且设计过程复杂.文献[30]第1次提出最优反步法的概念,在反步法的每一步应用强化学习中执行—评价结构,利用执行网络和评价网络分别产生控制律和评价控制性能,得到各子系统的最优虚拟控制器,从而使整个系统控制性能达到最优.文献[31—32]均采用最优反步法的控制设计思想,分别解决了船舶系统和含有未知动态的非线性系统的跟踪控制问题.然而,上述文献所提出的最优控制算法都是在假设被控系统状态完全已知的前提下设计的,但是,实际被控系统的部分状态往往难以通过测量直接获取.此外,现有的基于最优反步法的文献都忽略了对虚拟控制器反复求导所引起的“复杂度爆炸”问题.

值得注意的是,在实际工程中,由于系统部件的物理局限性,控制输入往往会受到约束,如果所设计的控制算法没有充分考虑这一问题,则无法获得理想的控制性能,甚至无法使得被控系统稳定.基于最优控制的优点,研究人员试图对系统中存在输入约束的优化问题进行处理,使系统在约束条件下达到控制目的,同时优化相应的性能指标[33—37].文献[35]针对具有输入约束的矿物研磨过程控制问题,通过引入参考调节器使得输入处于约束的范围内,同时应用强化学习策略,得到具有约束的最优调节器.文献[36—37]通过设计一种非二次型的效用函数,分别解决了具有输入约束的连续时间下系统模型自由的优化镇定问题和部分系统动态未知的事件触发优化问题.但以上方法需要假设系统状态完全可测,且未考虑高阶系统的跟踪问题.

为解决实际系统存在输入约束和不可测状态而导致难以实现最优控制的问题,本文基于强化学习方法提出一种最优跟踪控制策略.本文的主要贡献总结如下:1）针对高阶非线性系统,本文提出基于强化学习执行—评价结构的最优反步法控制策略,不仅能使系统输出快速跟踪理想信号,还能优化性能指标,降低控制资源的占用率.与文献[28]所提出的最优方法相比,本文所采用的设计方法更为简单,并能使虚拟控制序列均为最优.2）与文献[30]相比,本文所提出的最优跟踪控制方法不需要系统状态完全可测,放宽系统状态可测这一约束条件,更加符合实际工程情况.3）利用一种非二次型效用函数解决控制器约束问题.同时引入动态面技术,避免设计过程中“复杂度爆炸”的现象,简化控制器设计过程.

2 预备知识与问题阐述

2.1 系统描述

考虑一类严格反馈非线性系统

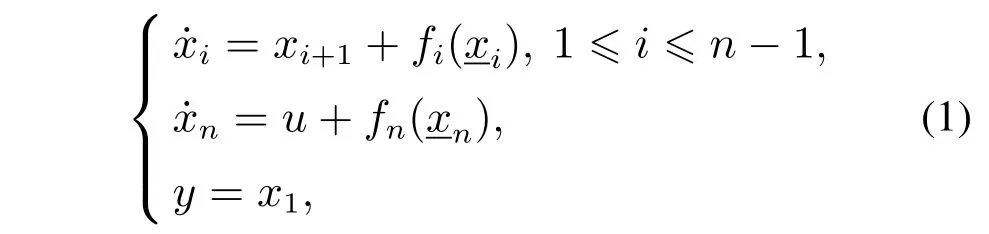
假设1[24]非线性函数f(x)在紧集Ωx内具有利普希茨特性,即存在一个已知的常数li,对于∀X1,X2∈Ri使得以下不等式成立:

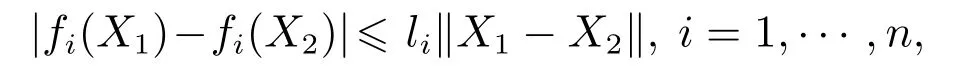
其中‖X‖表示向量X的2--范数.

引理1[17]根据神经网络的近似特性,任何定义在紧集Ωx上的连续非线性函数f(x)可以用神经网络逼近,具体形式如下:

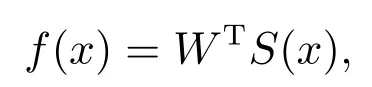
其中:W=[W1W2··· Wp]T∈Rp表示权值向量,S(x)=[s1(x)··· sp(x)]T为基函数向量,p表示神经元个数,

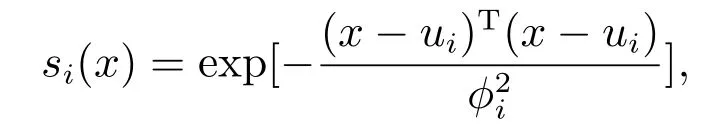
x ∈Ωx⊂Rp是输入向量,ui=[ui1··· uip]T是高斯函数的中心,ϕi是高斯函数宽度.基于神经网络逼近特性,存在理想权值向量W*,使以下方程成立:

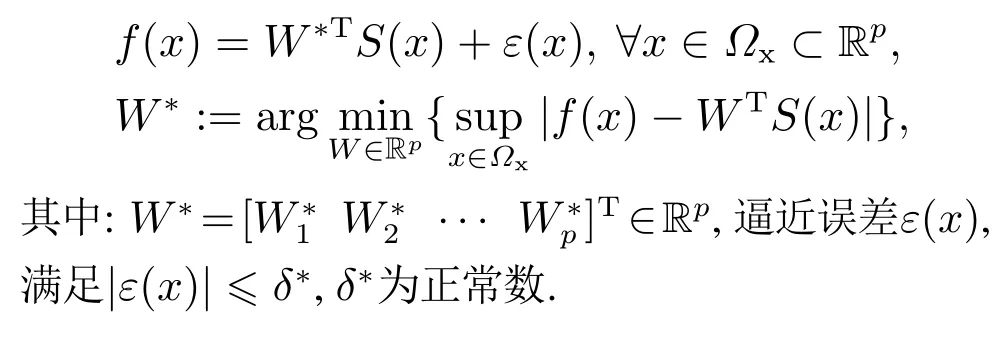
2.2 观测器设计

基于神经网络近似特性,可得

其中:

由于系统（1）中状态不可测,为了完成控制器设计,本文将设计如下状态观测器来估计系统状态:

定理1利用神经网络观测器（3）,若针对神经网络权值ˆWf设计如下自适应律:

其中:Sf=[Sf1Sf2··· Sfn]T,σ与η为正设计参数,则观测误差˜x与权值误差最终一致有界.

证选择如下李雅普诺夫函数:

其导数为

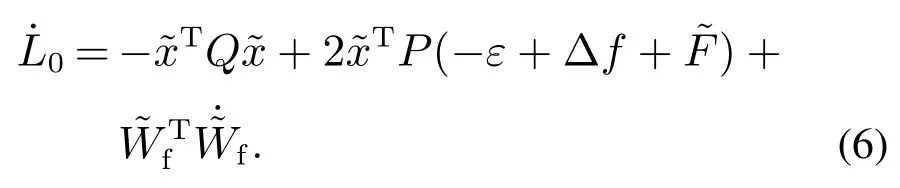
根据式（5）,并应用杨氏不等式,可得

注1系统（1）中的控制器u是在集合Ω上的容许控制器,即u在集合Ω上连续,u(0)=0,并且u可以使得系统（1）在Ω上稳定.定义为u ∈Ψ(Ω).本文所研究的最优问题是寻找一个满足约束条件的控制器u ∈Ψ(Ω),使得所设计的代价函数最小.

3 主要结果

3.1 最优控制器设计和稳定性分析

本节中,基于强化学习的最优反步法技术将应用于一类n阶非线性系统最优跟踪控制问题研究.不同于单一的反步法,最优反步法设计的控制器不仅能保证系统稳定,而且可以优化控制性能,设计算法结构如图1所示.

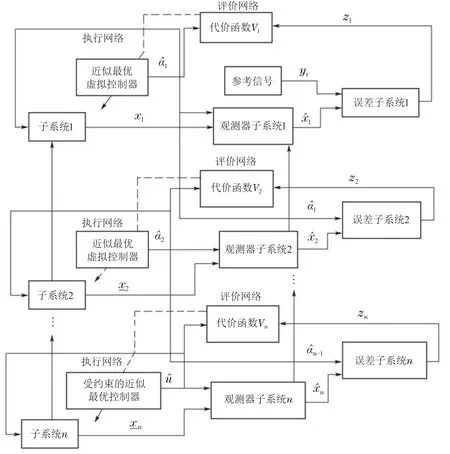
图1 基于强化学习的最优控制设计框图Fig.1 Block diagram of the optimal control design based on reinforcement learning

定义如下坐标变换:

步骤1跟踪误差z1对时间t的微分为

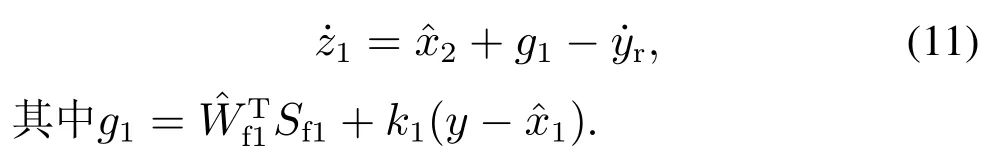
定义z1子系统代价函数为

将式（15）（17）代入式（13）得到

由式（10）,误差动态式（11）可改写为

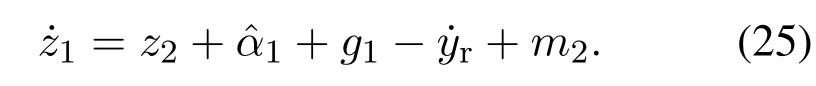
对z1子系统选择如下李雅普诺夫函数:

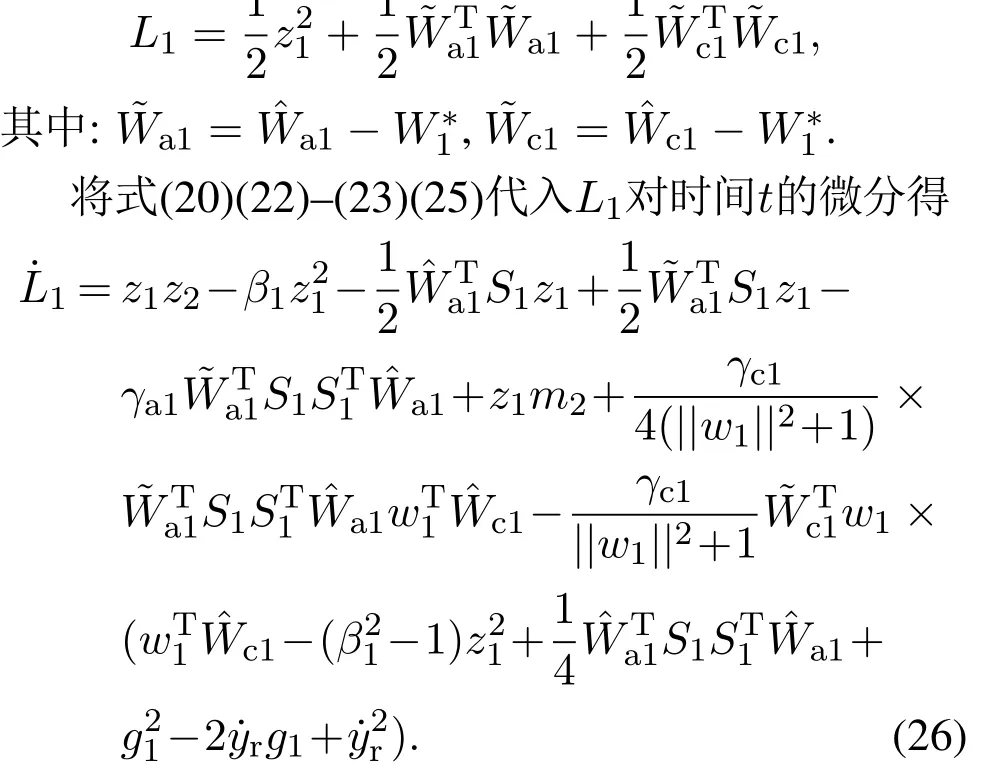
应用杨氏不等式和假设2,并结合式（18）（22）,式（26）可写为

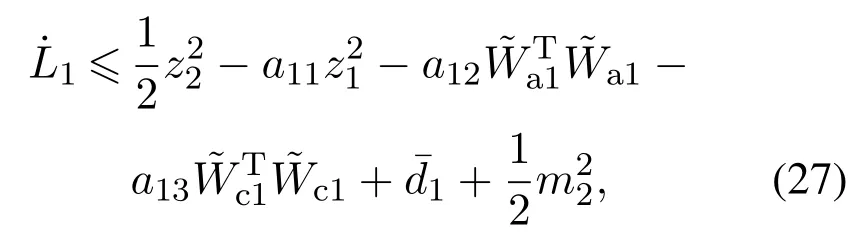
其中:

步骤2（i=2,3,···,n-1）基于动态面技术[25],选取如下一阶滤波器用于避免反步法中“复杂度爆炸”问题

注4每一步设计出相对应的后,在下一步的最优控制的设计中需对其进行求导,并且之后的每一步都会对其进行反复求导,从而产生“复杂度爆炸”问题.引入动态面技术将虚拟控制信号通过一阶低通滤波器得到估计值qi,在下一步设计过程中,用估计值代替虚拟控制信号可以避免对其进行求导,简化了控制器设计.

第i个子系统的误差动态方程为

βi为正设计参数,对应的HJB方程为

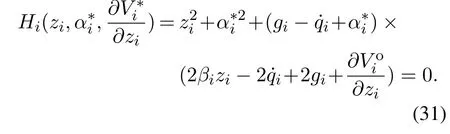
根据最优控制原理,最优虚拟控制器为

利用神经网络逼近性质

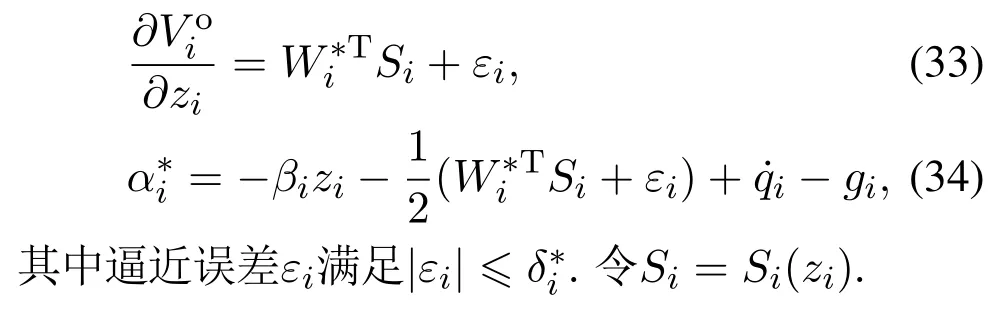
由式（31）（33）—（34）可知以下式子成立:

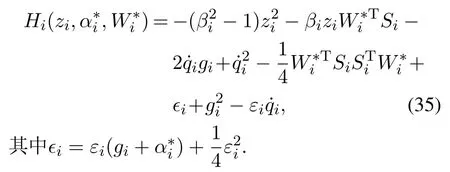
与第1步类似,式（33）—（34）可写为

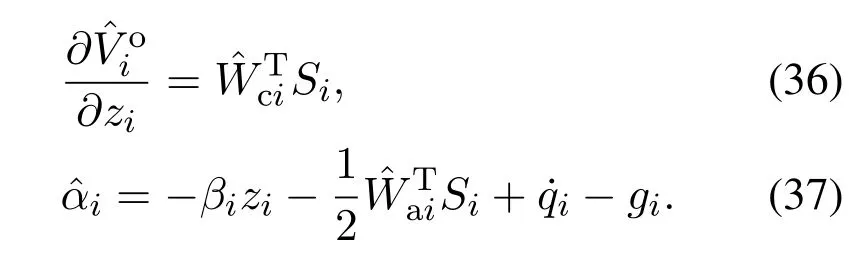
第i阶子系统的贝尔曼余差为

由式（10）可知第i阶系统误差动态为

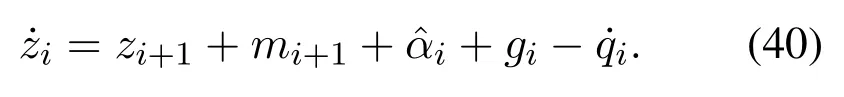
针对第i阶子系统选取如下李雅普诺夫函数:

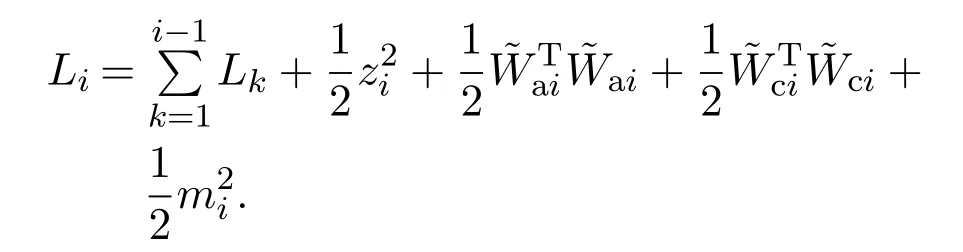
与第1步化简相似,Li对时间t求微分后可化简为ci为正参数.

步骤3根据式（10）,第n阶系统误差动态方程为

β为正常数.ψ(·)是一个有界且一阶导数为正常数的单调奇函数,满足|ψ(·)|≤1.当ψ(·)是单调奇函数时R(u)是正定的.不失一般性,本文选取ψ(·)=tanh(·).

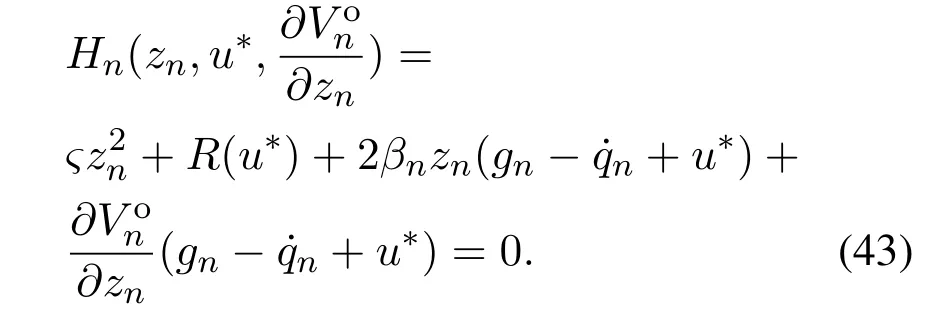
根据最优性原理,可得

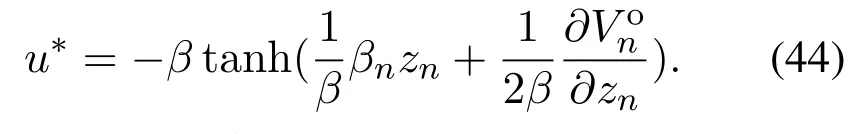
利用神经网络逼近性质

与第i步相似,式（44）—（45）可写为

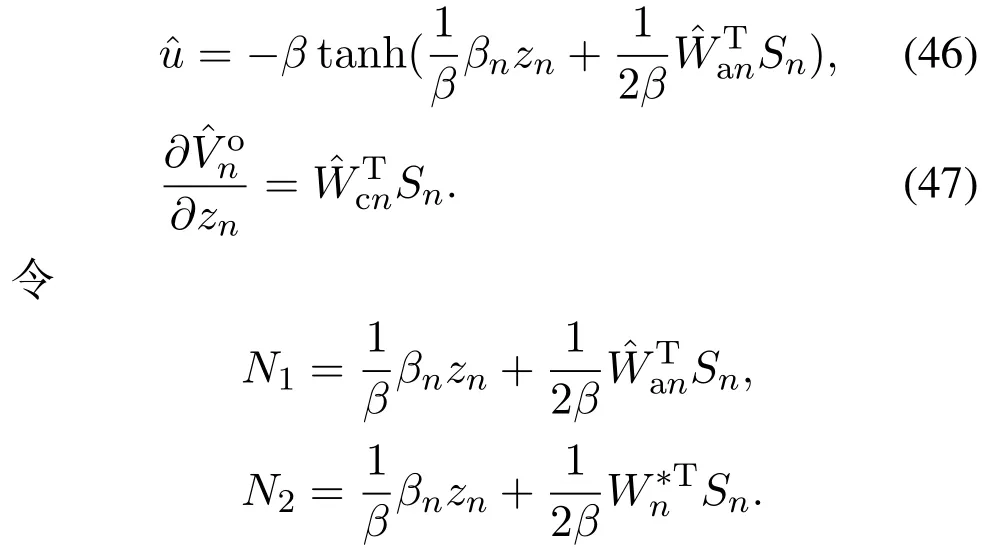
由式（43）（46）—（47）,可得第n阶子系统的贝尔曼余差为

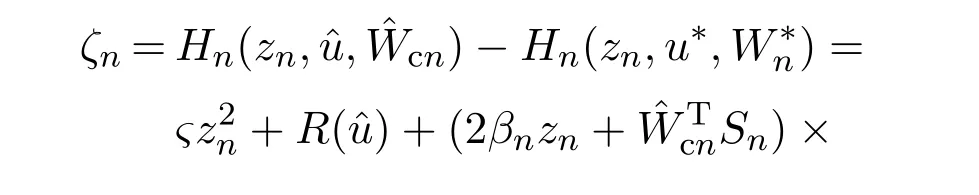
其中γan ＞0.

选取如下李雅普诺夫函数:

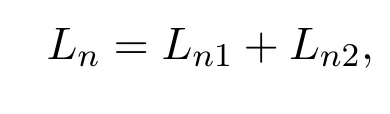
其中:

对Ln1微分可得

由式（43）（45）可得

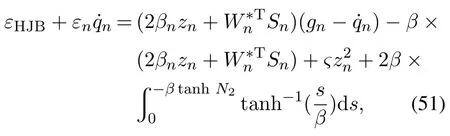
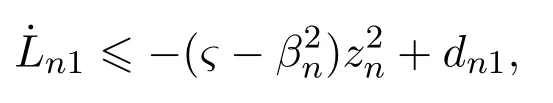
其中:

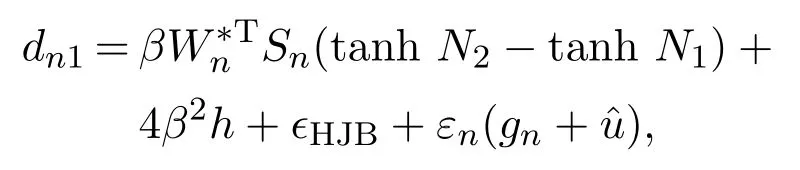
h为正常数.

由杨氏不等式可得

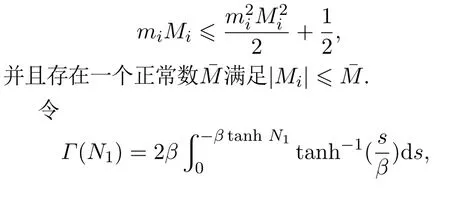
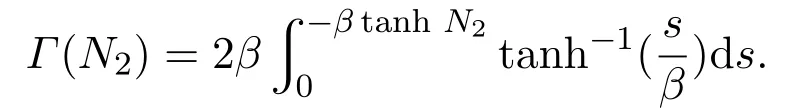
由文献[36]推导可知

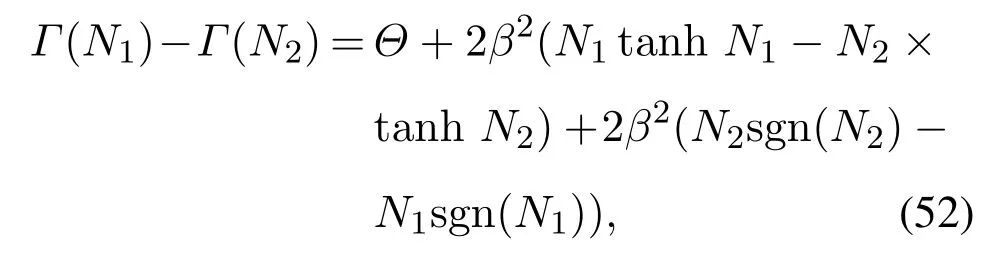
其中:

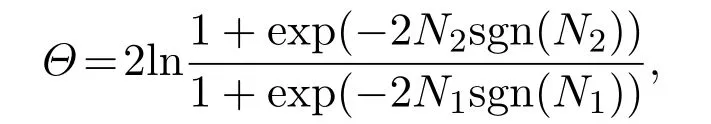
Θ为有界量.

对Ln求微分,并将式（48）—（49）代入,化简得

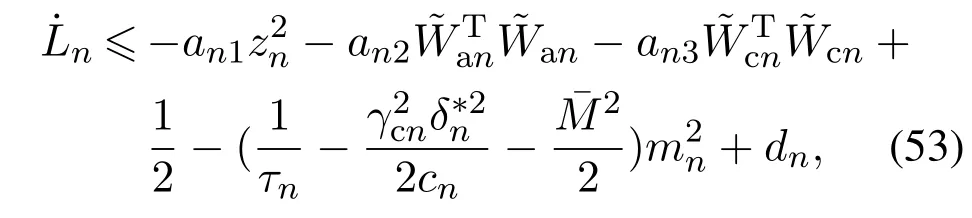
其中:

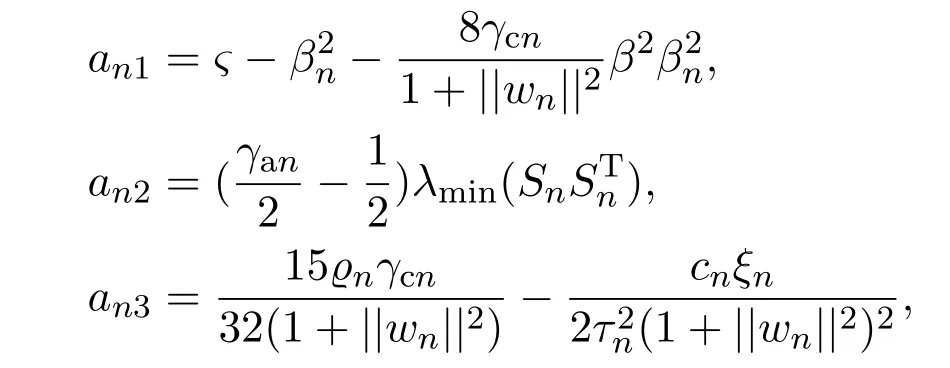
cn为正参数,且

选取李雅普诺夫函数

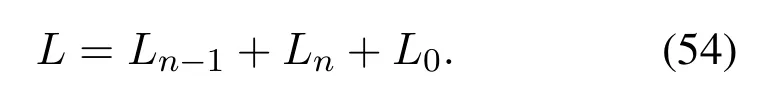
由式（7）（27）（41）（53）—（54）可知

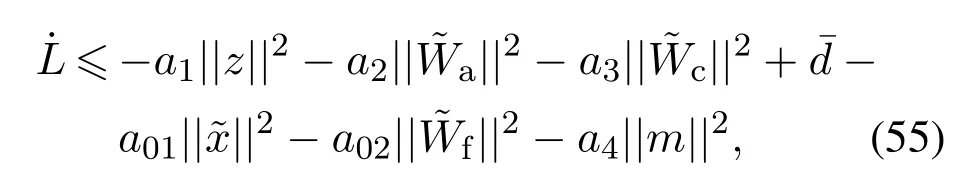
其中:

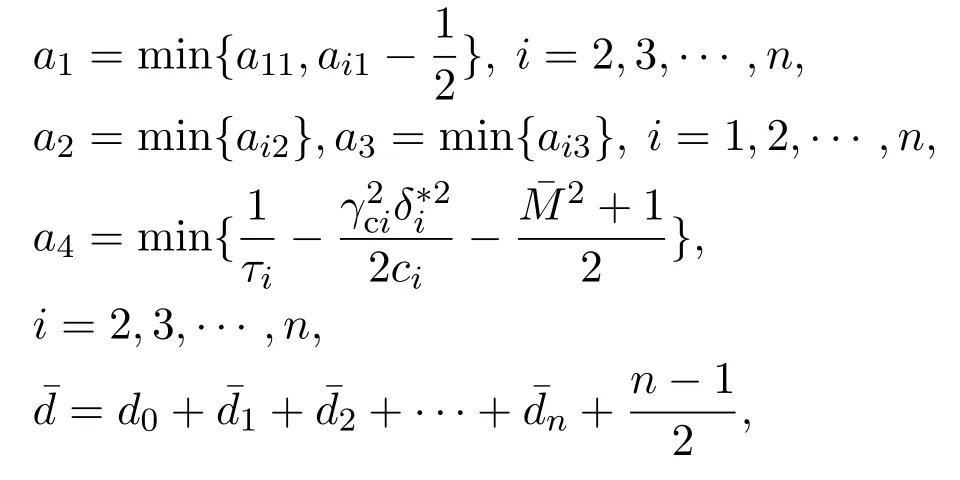
m=[m2m3··· mn]T.

由此可得

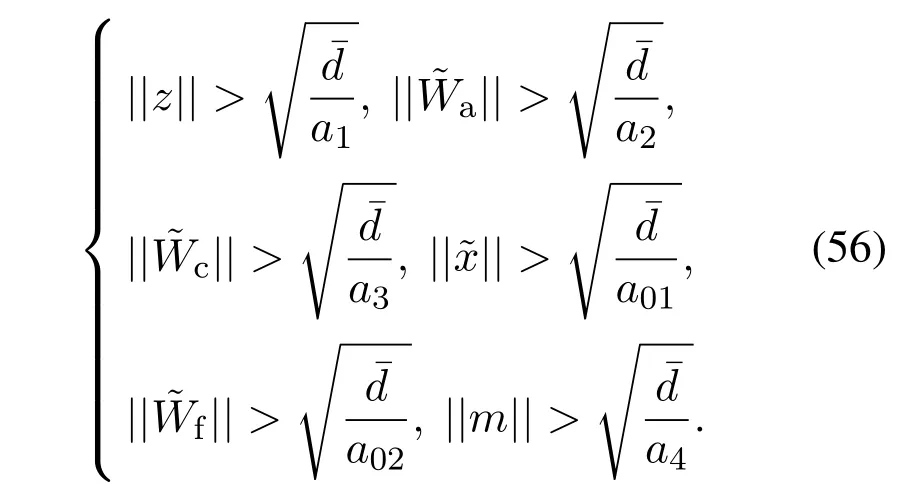
选取适当参数,使得a1,a2,a3,a4,a01,a02为正,且当上述不等式满足时,系统所有信号为一致最终有界.

3.2 数值仿真

本节将通过数值仿真验证所提出的基于强化学习最优控制方法的有效性.考虑如下系统:

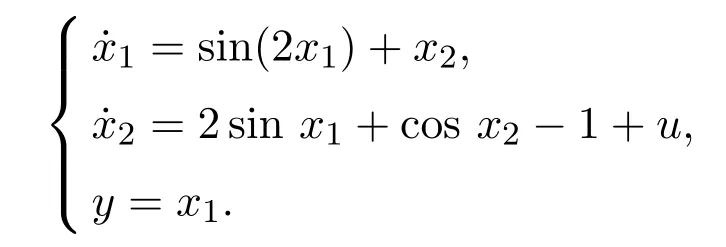
选取如下设计参数:

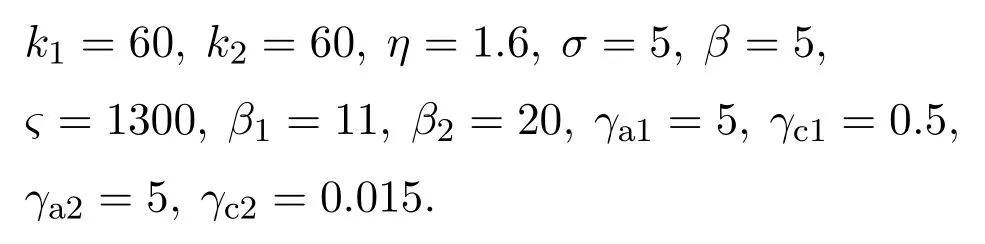
系统初始状态为

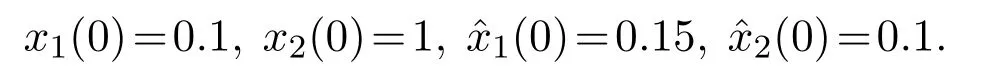
神经网络初始值选择为

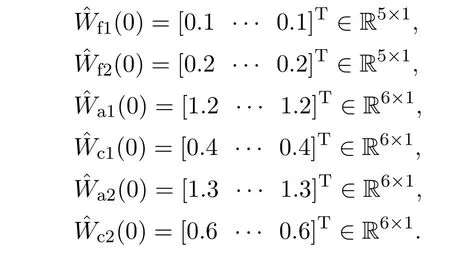
在学习过程的前5 s,给控制端施加一个噪声信号

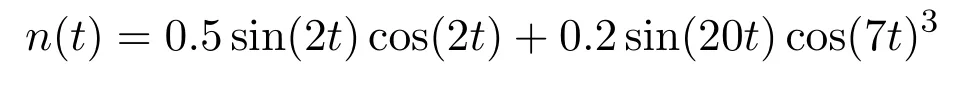
改善学习效果,理想跟踪信号yr=sint,图2—7为仿真结果.

图2 系统输出y和参考信号yrFig.2 System output y and reference signal yr

图3 观测器跟踪误差z1和观测误差Fig.3 The observer tracking error z1 and the observer error

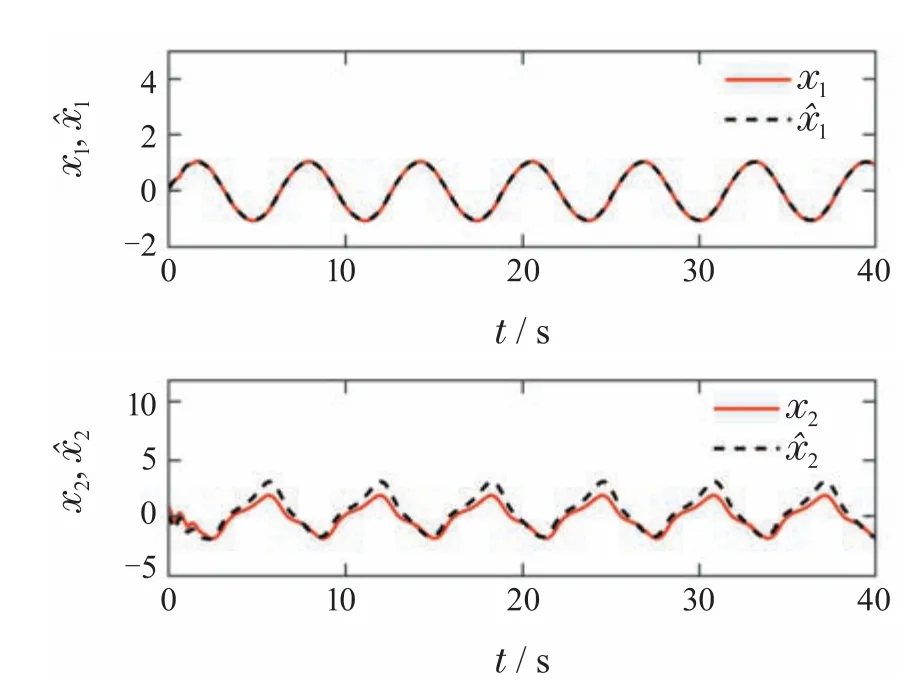
图4 状态x1,和状态x2,Fig.4 States x1, and x2,

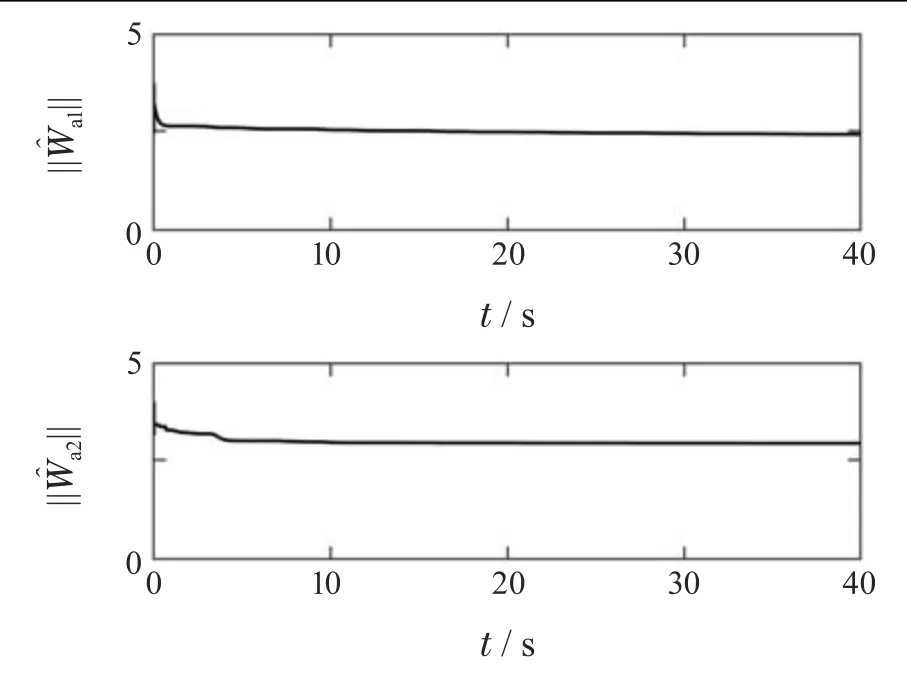
图5 自适应律||||和||||Fig.5 Adaptive laws||||and||||

图6 自适应律||||和||||Fig.6 Adaptive laws||||and||||

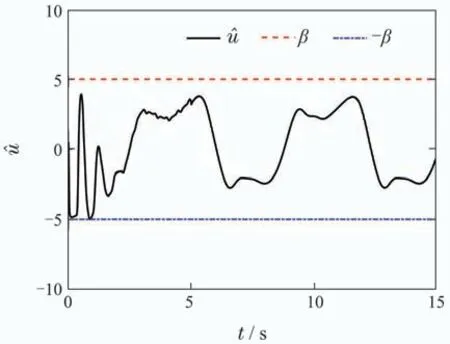
图7 系统输入Fig.7 System input

4 总结

本文针对存在不可测状态和输入约束系统的最优控制问题,基于反步法和强化学习的思想,提出了一种最优跟踪控制策略.首先,构建非线性观测器估计系统不可测状态,然后,在反步法中的每一步引入执行—评价网络结构的强化学习方法,得到相应的最优控制器,并通过引入动态面技术避免反步法中出现“复杂度爆炸”问题.最后,采用李雅普诺夫稳定性理论验证了闭环系统的稳定性.仿真结果表明了本文设计方法的有效性.在将来的研究工作中,我们将利用优化的思想解决多智能体系统最优编队控制问题.