独立点数为3的图的Z3-连通性

张小霞，余 鲲，黄明芳

(1.信阳师范学院 数学与统计学院，河南 信阳 464000;2.武汉理工大学 理学院，湖北 武汉 430070)

0 引言

本文所考虑的图都是有限的简单无环图.没有定义的术语及符号参见BONDY和MURTY的论著[1]。

设G是一个图，S是G的一个点集，若S中任意两点在G中都不相邻，则称S是独立集。G的最大独立集所包含点的个数被称为G的独立点数，用α(G)表示。对于两个子集A,B⊆V(G)，用e(A,B)来表示一个端点在A中、另一个端点在B中的所有边的个数。若A={v}，为了简单起见，用e(v,B)表示e({v},B)。图G的邻集用NG(x)表示，可简写为N(x)。

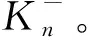
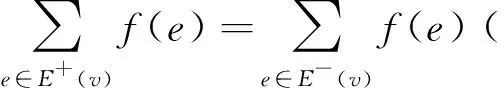
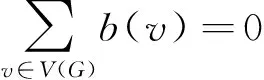
对每个点v∈V(G)都成立，则称图G是Zk-连通的。很显然，若图G是Z3-连通的,则存在处处非零3-流。

群连通的概念是“处处非零流”的推广，最早是由JAEGER等[2]引入的，并且提出了与3-流猜想相对应的Z3-连通猜想。

猜想(JAEGER等[2]) 每个5-边连通图都是Z3-连通的。

Z3-连通猜想的提出为3-流猜想的研究提供了另一思路。许多专家学者都对此做了大量研究，尤其是利用度条件来保证Z3-连通的存在性[3-5]。但直到2012年THOMASSEN[6]才对此猜想的研究取得突破性的进展，证明了每一个8-边连通图都是Z3-连通的。此结果很快被LOVASZ等[7]进一步改进，证明了每一个6-边连通图都是Z3-连通的。但目前，此猜想还没有解决。2016年YANG等[8]刻画了独立点数为2的图的Z3-连通性。受此启发，本文研究了独立点数为3的5-边连通图的Z3-连通性，证明了Jaeger的Z3-连通猜想对于独立点数为3且点连通度不大于5的图是成立的。

1 预备知识

引理1[2,9-11]设Z3为3阶循环群,则

(2)C2是Z3-连通的。

(3)W2k是Z3-连通的，其中k为正整数。

设H是图G的一个子图，若把H中的所有点都粘在一起，并把此过程所产生的所有环都删掉，则称G收缩H，记为G/H。

引理2[9,10]设H为G的一个Z3-连通子图。若G/H是Z3-连通的，则G也是Z3-连通的。

由文献[8]中定理1.3，容易得出如下结论:

引理3 设G是一个δ(G)≥4的2-边连通简单图。若α(G)≤2，则G是Z3-连通的。

设NG(v)={v1,v2,…,vm}(m≥4)。如果将vv1和vv2两条边去掉，添加一条新边v1v2所得到的图记为G[vv1,vv2]，则有下面结论成立。

引理4[11]如果G[vv1,vv2]是Z3-连通的，那么图G也是Z3-连通的。

引理5 设G是5-边连通图并且α(G)=3。若G包含极大Z3-连通子图H且α(G-H)≤2，那么图G是Z3-连通的。

证明设G*=G/H，v*为收缩H所形成的新点，则α(G*-v*)=α(G-H)≤2。设e为G*-v*的一条割边，G1和G2是G*-v*-e的两个连通分支，则α(G1)=α(G2)=1。因为G是5-边连通图，所以G*中v*的度dG*(v*)≥5并且G*-v*的最小度δ(G*-v*)≥4。于是G1和G2都是阶数大于等于5的完全图并且e(v*,G1)≥2或者e(v*,G2)≥2。由引理1和引理2可知，G1+H或者G2+H是Z3-连通的，这与H是极大Z3-连通子图矛盾！因此G*-v*是2-边连通的。由引理3知，G*-v*是Z3-连通的。再根据引理2，从而G也是Z3-连通的。证毕。

2 主要结论

定理1 设G是5-边连通图。如果α(G)=3并且点连通度κ(G)≤4，那么图G是Z3-连通的。

证明设S为图G的最小点割，G1和G2为G-S的两个分支，则α(G1)+α(G2)≤3。因此α(G1)=1或α(G2)=1。

不失一般性，假设α(G1)=1即G1=Km(m≥1)并且假设图G不是Z3-连通的。

断言1 不存在点v∈S使得G1+v是Z3-连通的。

断言1的证明 假设存在点v∈S使得G1+v是Z3-连通的，则由引理1可知|V(G1)|≥4。设H是图G中包含G1+v的极大Z3-连通子图。若H∩G2≠∅，则显然有α(G-H)≤α(G2)=2。若H∩G2=∅，则α(G-H)≤2。否则假设α(G-H)=3，注意到对任意点x∈V(G-H)，都有e(x,H)≤1，所以必存在u∈V(H)使得α(G)=4，矛盾！由引理5可知，G是Z3-连通的，矛盾！故断言1成立。

断言2 2≤m≤4且κ(G)=4。

断言2的证明 因为G是5-边连通图并且κ(G)≤4，所以可得m≠1并且存在点v∈S使得e(v,G1)≥2。如果m≥5，由引理1和2可知，G1+v是Z3-连通的，与断言1矛盾！故2≤m≤4。这也意味着κ(G)≠1。

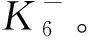
当m=4时，对任意v∈S，由断言1可知e(v,G1)≤2。又因为|S|=4并且e(G1,S)≥8，所以e(v,G1)=2。设N(v)∩G1={v1,v2}。下面考虑图G[vv1,vv2]。设H=G1+S-v+v1v2。很明显，它是Z3-连通的。再设G*=G[vv1,vv2]/H且v*是收缩H而形成的新点。易知S中无相邻边，因此d(v*)≥7并且G*-v是4-边连通的。如果存在两个点u,w∈V(G2)使得{u,w,v*}是一个独立集，那么必然存x,y∈V(H)使得{u,w,x,y}是图G的独立集，这与α(G)=3矛盾！因此α(G*-v)≤2。由引理3可知，G*-v是Z3-连通的。由引理1和2可知，G[vv1,vv2]是Z3-连通的。再根据引理5，G也是Z3-连通的，矛盾！

当m=3时，由断言1可知，最多有一个点v∈S使得e(v,G1)≥3。而由于e(G1,S)≥9，所以e(v,G1)≥2，v∈S。因为α(G)=3，所以G[S]一定包含一条边，不妨设为xy。若e(x,G1)=3或e(y,G1)=3，则G1+{x,y}包含Z3-连通子图W4作为生成子图，与断言1矛盾！故e(x,G1)=2和e(y,G1)=2，并且

|N(x)∩N(y)∩V(G1)|=1。

而此时，G1+{x,y}也包含W4作为一个生成子图，因而是Z3-连通的，仍然与断言1矛盾！

当m=2时，设V(G1)={v1,v2}，则

|N(v1)∩N(v2)|=S。

任意选取v∈S，考虑图G[vv1,vv2]。与m=4时类似，也可证明G是Z3-连通的，与断言1矛盾！证毕。

3 结束语

文献[12]完美地刻画了独立点数为2的图的Z3-连通性，同时猜想：独立点数为3的5-边连通图是Z3-连通的。本文证明了此猜想在点连通度小于等于4时是成立的。对于点连通度等于5的情况还在进一步研究当中,旨在推广LI等[13]所做的关于独立点数为3的处处非零3-流的结论。