超低有质动力势能场中原子强场双电离机制研究

李盈傧，何锦锦，陈红梅，李怡涵，秦玲玲，许景焜， 史璐珂，翟春洋，汤清彬，余本海

(信阳师范学院 物理电子工程学院, 河南 信阳 464000)

0 引言

超快、超强激光脉冲与原子分子相互作用可以出现许多有趣的非线性过程, 比如阈上电离[1]、 高次谐波的产生[2]、 受挫双电离[3]、 强场双电离等。 对于强场双电离, 通常可以由两种机制发生:次序双电离(sequential double ionization, SDI)[4]和非次序双电离(nonsequential double ionization, NSDI)[5]。 当激光强度较高/椭偏光/圆偏光下, 双电离主要通过SDI机制发生, 该过程可以基于隧穿理论来很好地解释[6]。 当激光强度较低/线偏光下, 双电离主要通过NSDI机制发生。 该过程可以利用三步再碰撞理论来解释[7]。 在三步再碰撞过程中, 第一个电子的最大返回能量约为3.17Up, 其中Up∝Iλ2为有质动力势能,I和λ分别为激光强度和波长。 以前的研究表明, 碰撞之后两个电子的电离过程强烈依赖于返回能量: 当第一个电子的返回能量大于第二个电子的电离能时, 第二个电子能够通过直接碰撞电离通道(recollision-impact ionization (RII))电离[8]; 当第一个电子的返回能量小于第二个电子的电离能时, 碰撞不足以使第二个电子直接电离, 第二个电子只能通过碰撞激发电离通道(recollision excitation with subsequent ionization (RESI))电离。 因此, NSDI的微观动力学过程对激光强度和波长均有很强的依赖。

过去人们主要研究了较高有质动力势能场中原子分子NSDI电子关联动态过程。 比如, 对于中红外激光场, 当激光强度较高时, 实验上观测到Xe2+离子的纵向动量分布呈现双峰结构, 并且Xe原子NSDI的关联电子动量分布呈现“十字型”结构, 这表明 RII和RESI两个通道同时存在[9]; 当激光强度超低时, 随着激光强度的增加, 实验上观测到Xe2+离子的纵向动量分布由零动量附近的平台结构转变为双峰结构, 半经典理论研究表明双峰结构产生的原因是RII通道的主导作用[10]。 对于近红外激光场, 当激光强度较高时, 实验发现He原子NSDI的关联电子动量分布呈现V型结构[11], 经典理论研究表明该结构产生的原因是碰撞过程中两个电子之间不均匀的能量分配[12]; 当激光强度超低时, 半经典理论研究表明产生V型结构的原因是碰撞后母核离子对电子的库仑吸引及末态电子之间的排斥作用[13]。 对于较短波长的激光场, 实验发现He原子NSDI的双电离电子获得的末态能量大于2Up[14], 经典理论研究表明, 当激光强度较高时, 产生高能电子的原因是母核离子的库仑力对电子的弹射作用, 从而使两个电子获得较高的末态能量[15]; 当激光强度超低时, 产生高能电子的原因是母核离子的库仑力及电场力的共同作用使得电子能够在较长的一段时间内连续加速, 从而获得较高的末态能量[16]。 然而, 在较短波长且激光强度超低时, 有质动力势能相比于原子的第二电离能更低, 这种情况下双电离如何发生? 目前尚不清楚。

本文利用三维经典系综模型, 研究超低有质动力势能场下碱土金属原子的强场双电离。 对于较高有质动力势能场, 双电离产率随原子电离能的增大而减小, 而对于超低有质动力势能场, 双电离产率随原子电离能的增大而增大, 前者可以由三步再碰撞机制来很好地解释, 而后者却很难解释。 反演分析表明, 在超低有质动力势能场中, 两电子发生“缩小版回碰”即回碰的整个过程均发生在核的有效区域内;然后详细分析在超低有质动力势能场中第二个电子的电离过程;最后讨论了“缩小版回碰”过程对激光波长的依赖关系。

1 理论方法

精确描述原子分子强场双电离需要数值求解含时薛定谔方程[17], 但该方法计算量非常大, 目前的计算技术仍很难实现。 相比较来说, 经典系综[18]模型既可以克服计算量大的问题, 又可以通过反演分析直观地展示双电离的整个过程, 已经被广泛用来研究强场双电离。 近年来, 经典模型在揭示原子分子强场双电离超快电子动力学过程中发挥了巨大作用。 因此, 利用三维经典系综模型研究原子强场双电离, 在三维经典系综模型中, 两电子的演化遵循牛顿耦合运动方程(本文均采用原子单位, 除非特殊说明):

(1)

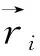
(2)

式 (2) 中, 对于不同的原子种类, 软核参数a有一个合适的取值范围, 在这个区间范围内a的取值对结果没有影响, 在本文中, 对于Mg原子,a=3 a.u.; 对于Ca原子,a=3.8 a.u.; 对于Sr原子,a=4 a.u.; 对于Ba原子,a=4.3 a.u.， 为避免数值计算中的奇点,b通常取很小值, 本文b=0.1 a.u.。

为获得初始系综, 首先随机将两电子放在原子核附近, 然后给两电子一个确定的动能, 使得系统的总能量Etot等于目标原子的第一电离能Ip1和第二电离能Ip2的负和:

(3)

对于Mg、Ca、Sr、Ba原子,Etot分别为-0.83、-0.66、-0.61、-0.56 a.u.。 随后两电子只在库仑场的作用下, 按照牛顿运动方程演化足够长的时间 (100 a.u.), 可以得到稳定的初始系综分布。 然后, 打开激光场, 两电子在库仑场和激光电场的共同作用下, 仍按照牛顿运动方程演化。 当激光脉冲结束时, 统计所有电子对的能量 (包括动能、母核离子与电子间势能、电子与电子间势能的一半), 如果两电子的能量均为正, 则被定义为双电离事件。

2 结果和讨论

图1(a)和图1(b)给出了有质动力势能Up随激光强度的变化曲线, 对应的波长分别为400 nm和2 000 nm, 水平直线代表碱土金属原子的第二电离能即Ip2。 比较图1(a)和图1(b)知, 当波长为400 nm时, 有质动力势能远低于碱土金属原子的第二电离能。 图1(c)和图1(d)分别给出了400 nm及2 000 nm下碱土金属原子的双电离产率曲线, 其中黑色圆圈、红色方框、蓝色三角、绿色菱形分别代表Mg、Ca、Sr、Ba原子。 比较图1(c)和图1(d)可知, 超低有质动力势能场与较高有质动力势能场下, 双电离产率随激光强度的变化曲线呈现明显不同的特征。 对于较高的有质动力势能场, 双电离产率随原子电离能的增大而减小; 而对于超低的有质动力势能场, 双电离产率随原子电离能的增大而增大。 前者可以由三步再碰撞机制来很好地理解, 因为当回碰能量一定时, 原子的Ip2越大, 第二个电子往往需要第一个电子传递更多的能量才能电离, 因此不容易发生电离。 而后者很难用再碰撞机制来理解。

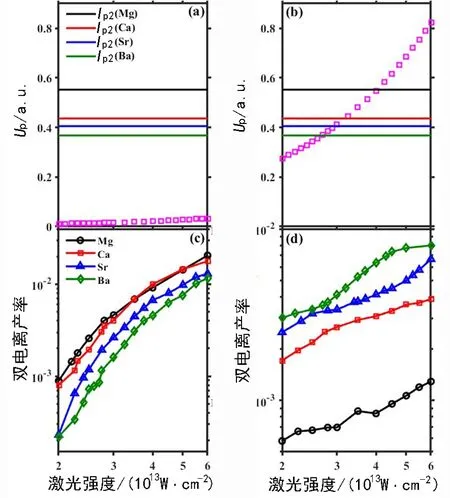
图1 有质动力势能和双电离产率随着400 nm和 2 000 nm激光场强度的变化曲线Fig. 1 Up and probabilities of DI as a function of laser intensity for 400 nm and 2 000 nm laser fields

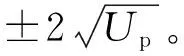
图1的双电离产率和图2的两电子末态动量均表明在超低有质动力势能场下电子超快动力学行为显示较新颖的特性。 文献[19-20]分别在实验上研究了800 nm 及2 000 nm碱土金属原子的强场双电离, 证实了较高有质动力势能场下, 双电离机制仍然可以用再碰撞机制来解释。 以下, 我们将从经典力学出发, 理解超低有质动力势能场下原子双电离过程。

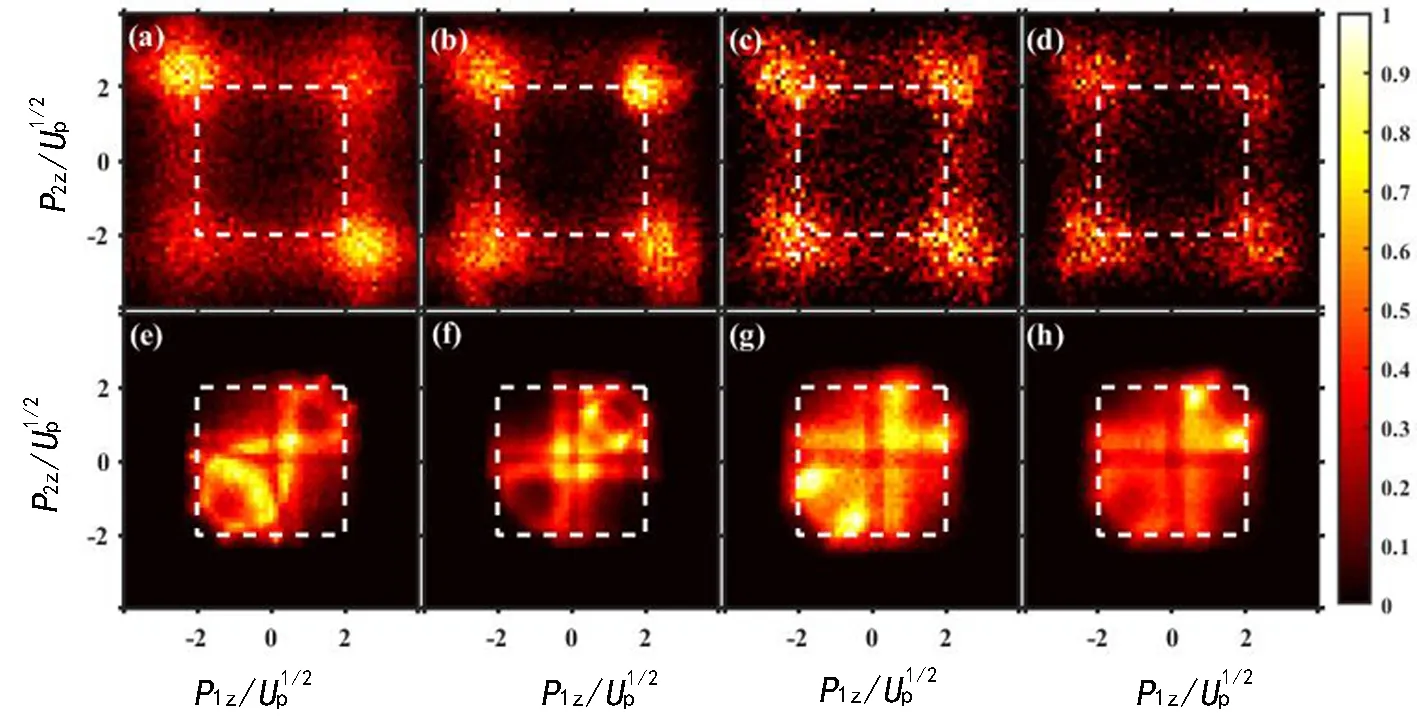
图2 两电子沿激光偏振方向的末态动量谱Fig. 2 Electron momentum distributions of two electrons

为了直观地揭示超低有质动力势能场下原子双电离微观动力学过程。 图3给出了两电子的能量随时间演化的典型轨迹及两电子的二维空间轨迹, 并给出较高有质动力势能场的情况作为对比。

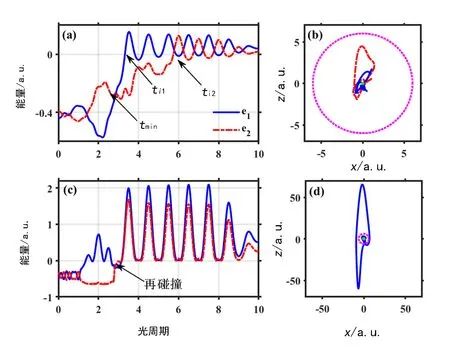
图3 两电子的能量轨迹和二维空间轨迹Fig. 3 The energy and space trajectories of the two electrons

图3中，蓝色实线代表第一个电子(e1)即先发生电离, 红色虚线代表第二个电子(e2) 即后发生电离。 (a)(b) 波长为400 nm, (c)(d) 波长为2 000 nm。 激光强度为2×1013W/cm2。 右列虚线圆形的半径为6 a.u., 代表电子处于电离态和束缚态的界线, 即圆形内的区域表示电子处于束缚态, 圆形外的区域表示电子处于电离态。 图3(a)和图3(b)对应超低有质动力势能场,tmin定义为有效碰撞时间即第一个电子的能量首次为正前两电子相距最近的时间,ti1定义为有效碰撞后第一个电子的能量首次为正的时间,ti2定义为有效碰撞后第二个电子的能量首次为正的时间。 图3(b)给出了两电子从开始到有效碰撞时刻的演化轨迹。 图3(c)和图3(d)对应较高有质动力势能场, 箭头标注出了再碰撞时间, 再碰撞时间定义为第一个电子电离后，返回母核离子时, 与第二个电子相距最近的时刻。 图3(d)给出了两电子从开始到再碰撞时刻的演化轨迹。 比较图3(a)和图3(c)可知, 在较高有质动力势能场下, 如图3(c)所示, e1首先发生电离, 然后返回到母核离子附近并发生再碰撞, 传递能量给e2导致其电离。 从图3(d)中也可以看出, e1先发射到圆形区域外, 然后又返回圆形区域内发生碰撞, 这是典型的再碰撞过程。 有趣的是, 在超低有质动力势能场下, 如图3(a)所示, 两电子在tmin时刻首先发生有效碰撞, 然后处于较高激发态的电子即e1于ti1时刻电离, 处于超低激发态的电子即e2需在激光场中演化更长时间,从而吸收更多的能量于ti2时刻电离。 从图3(b)可以清楚的看到, 两电子均未脱离母核离子束缚前发生有效碰撞, 没有回碰过程。 因此, 通过分析两电子的经典轨迹可知, 较高有质动力势能场下双电离过程可以由回碰机制来解释, 然而超低有质动力势能场下双电离过程很难用回碰机制来解释。 为了揭示超低有质动力势能场中原子双电离电子微观动力学过程的更多细节, 图4给出了有效碰撞时间(tmin)、第一个电子能量首次为正的时间(ti1)及第二个电子能量首次为正的时间(ti2)的归一化概率分布。 波长为400 nm, 激光强度为2×1013W/cm2。 由图4(a)可知, 有效碰撞时间tmin主要分布在激光场零值附近, 这表明两电子在电场零值附近可以最有效的传递能量。 从图4(b)和图4(c)可以看出, 两电子的电离时间主要发生在激光场峰值附近。从半个光周期来看, 两电子的电离时间概率分布明显不同。对于ti1, 其概率分布呈现单峰结构, 而对于ti2, 其概率分布呈现明显的双峰结构, 即P1峰和P2峰。这表明, 在超低有质动力势能场中两电子有明显不同的动力学特征。

图5(a)给出了有效碰撞时间tmin与第一个电子能量首次为正时间ti1之间的时间延迟分布即(ti1-tmin), 图5(b)给出了有效碰撞时间与第二个电子能量首次为正的时间ti2之间的时间延迟分布即(ti2-tmin)。 比较图5(a)和图5(b)可知, (ti1-tmin)往往小于3个光周期, 其概率的最高峰位于1个光周期附近。 (ti2-tmin)往往大于3个光周期, 其概率的最高峰位于3.5和5个光周期附近。 这意味着两电子发生有效碰撞后, 第一个电子往往可以在较短时间内电离, 而第二个电子则需要经过更长时间电离。 这主要是因为, 两电子发生有效碰撞后, 第一个电子往往处于较高的激发态, 在较短的时间内即可吸收足够的能量脱离母核离子的束缚。 然而, 第二个电子往往处于超低的激发态, 需经过更长的时间才可以吸收足够多的能量脱离母核离子的束缚。 因此, 第一个电子电离主要因为有效碰撞的作用, 而第二个电子电离则主要因为激光场的作用。

图4 时间分布Fig. 4 Time distribution

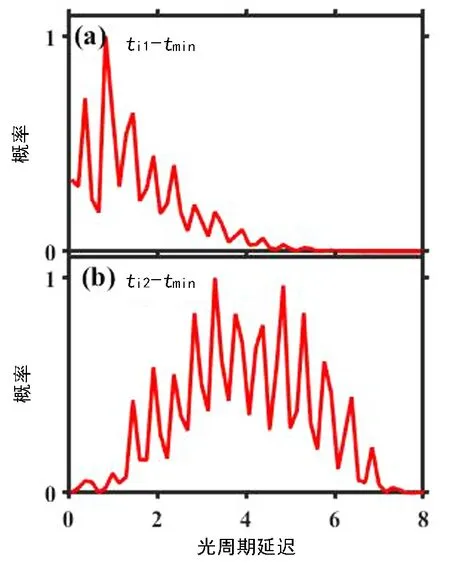
图5 时间延迟分布Fig. 5 Time delay distribution

为了理解第二个电子的电离时间在半个光周期内呈现的双峰结构即图4(c)标注的P1和P2, 进一步把双电离轨迹分为两类。 A: P1峰对应的双电离轨迹; B: P2峰对应的双电离轨迹。 然后分别分析了事件A和B对应的经典轨迹, 图6(a)和图6(b)给出了两电子的能量随时间的演化, 图6(c)和图6(d)给出了电子与母核离子间的距离随时间的演化, 其中蓝色实线代表第一个电子, 红色虚线代表第二个电子, 竖直双向箭头标注出第二个电子能量首次为正的时间即ti2。 由图6(a)和图6(c)可知, 对于轨迹A, 第二个电子的能量首次为正后, 电子逐渐远离母核离子, 并完全脱离母核离子的束缚。 由图6(b)和图6(d)可知, 对于轨迹B, 第二个电子的能量首次为正后, 电子远离母核离子, 然而经过较短的时间, 再次被束缚, 随后经过大约3个光周期, 能量再次为正, 之后电子逐渐远离母核离子并“真正”脱离束缚。 为了解释第二个电子之所以呈现出这两种过程, 我们统计了当第二个电子的能量首次为正时事件A和事件B对应的第二个电子的速度, 如图7所示, 红色虚线代表事件A, 蓝色实线代表事件B。 比较这两种事件可知, 对于事件B, 能量首次为正时, 第二个电子的速度往往更小一些。 因此, 当电子的能量首次为正后, 对于事件B, 由于电子电离时刻速度较小, 在母核离子的库仑吸引作用下更容易被“拉回”, 随后通过在激光场中积累足够的能量,从而彻底克服库仑束缚而电离。

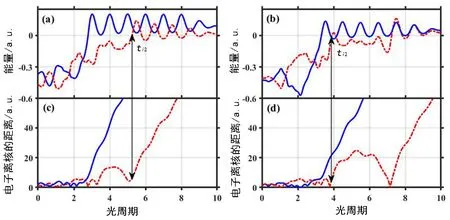
图6 两电子的轨迹图Fig. 6 The trajectories of the two electrons

图7 第二个电子电离时刻的速度分布Fig. 7 The velocity distribution of the second electron at ionization moment

为了进一步理解超低有质动力势能场下第二个电子在激光场中如何发生电离, 追踪分析了第二个电子从有效碰撞时刻tmin到能量首次为正时刻ti2的轨迹, 如图8所示, 其中图8(a)给出了电子与母核离子间的距离随时间的演化, 图8(b)给

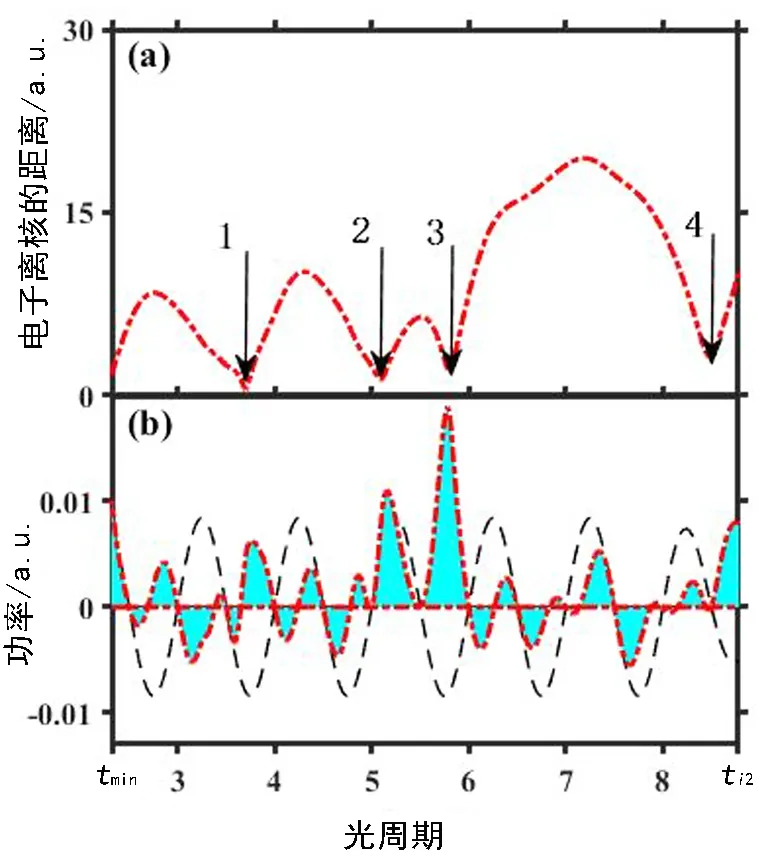
图8 第二个电子离核的距离及其功率随时间的演化Fig. 8 The distance of the second electron from the nucleus andits power as a function of time

出了电子的功率随时间的演化, 竖直箭头代表电子返回母核离子的时刻, 阴影部分表示电场对电子所做的功。 从图中可以看出, 从tmin到ti2, 第二个电子需要往返母核离子四次, 电场对电子所做的功尽管有时为正有时为负, 但正功的贡献要比负功的贡献大得多, 从而电子可积累足够多的能量脱离母核离子的束缚。 最后, 以Mg原子为代表, 图9给出了“再碰撞”和“缩小版回碰”这两种通道的相对贡献随激光波长的变化曲线。

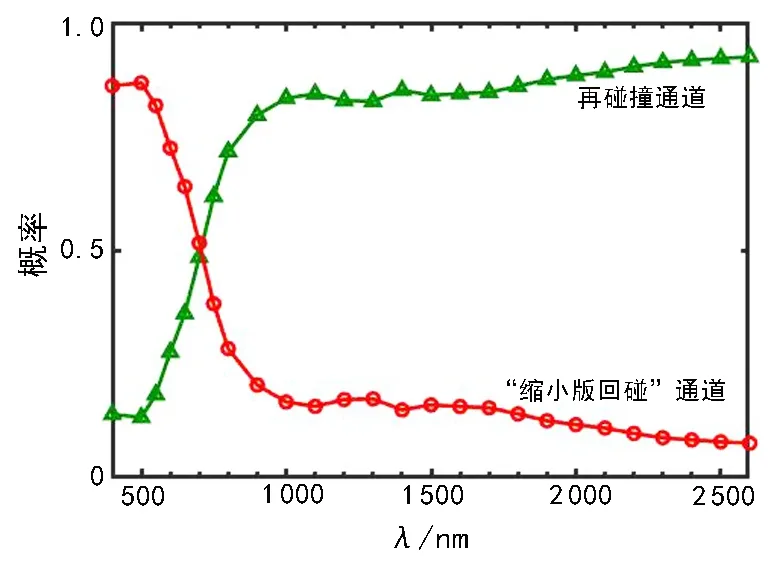
图9 两种通道随激光波长的变化Fig. 9 The two channels as a function of the wavelength

图9中，绿色三角表示再碰撞通道贡献的双电离概率, 红色圆圈表示“缩小版回碰”通道贡献的双电离概率。激光强度为2×1013W/cm2。对于超低激光强度, 当波长较短时, “缩小版回碰”通道占主导, 当波长较长时, 再碰撞通道占主导。 因此, 这两种双电离通道往往同时存在, 相对贡献依赖于激光参数。

3 结论

超低有质动力势能场中双电离产率随原子电离能的增大而增大, 并且两电子末态获得的能量往往都大于2Up。 这些新颖的结果很难用再碰撞机制来解释。 追踪分析双电离的轨迹表明, 在超低有质动力势能场中, 两电子首先发生“缩小版回碰”过程, 然后处于较高激发态电子在激光场的峰值附近先电离; 处于超低激发态的电子, 往往需要通过多次往返母核离子, 并在激光场的共同作用下来积累足够的能量电离。 进一步研究表明, 在超低激光强度下，波长较短时，双电离由“缩小版回碰”通道起主导作用, 而波长较长时，则由再碰撞通道起主导作用。 激光强度和激光波长是研究双电离过程的两个重要指标, 此工作为后期的理论和实验研究低激光强度以及短波长的双电离工作提供了指引。