宫颈癌放射治疗的数学模型研究
2022-01-27庞留勇李秋英
庞留勇,赵 中,李秋英
(黄淮学院 数学与统计学院,河南 驻马店 463000)
0 引言
宫颈癌(Cervical Cancer)是女性中发病率较高的恶性肿瘤。2018年全世界大约有57万新发病例,其中31万的患者死于宫颈癌,我国宫颈癌发病率高居世界第二位,仅次于智利[1-3]。近年来我国宫颈癌的平均发病率呈现上升趋势,并且发病年龄逐渐趋于年轻化,平均发病年龄从20年前的67岁降到现在的45岁,甚至有17至18岁的病患。宫颈癌已成为我国当前威胁女性健康的重大公共卫生问题。目前放射治疗已经成为宫颈癌的主要治疗手段。体外实验分析表明,细胞周期动力学极大地影响放射敏感性,快速分裂的肿瘤细胞对放射治疗是非常敏感的,而处于休眠期或者缓慢分裂的肿瘤细胞对放射治疗的敏感性比较弱[4-6]。
数学建模方法已经成为肿瘤生长机理分析、治疗方案设计及治疗效果评估的重要的手段。1956年,PUCK和MARCUS[7]通过哺乳动物体外培养细胞的放射存活曲线,研究了细胞存活率与照射剂量的定量关系,提出了线性二次模型(LQ model),指出细胞存活率与放射剂剂量满足:lns=f(d),即
s=exp(f(d))=
exp(-αd-βd2),
(1)
其中s是使用剂量为d的单次放射治疗后肿瘤细胞的存活比例。
随着研究的深入,该模型逐步运用到基于临床和实验数据的肿瘤体积演变过程的研究中[8-10]。例如,2009年,CHVETSOV等[11]将肿瘤细胞分为具有增生能力的富氧细胞和乏氧细胞、由放射治疗所导致的死亡富氧细胞和乏氧细胞4个子群,利用差分方程建立了具有放射治疗的肿瘤生长四仓室模型,较好地模拟了肿瘤患者的放射治疗时序影像数据。2016年,BELFATTO等[12]利用16位宫颈癌患者不同时序的CT图像数据对放射治疗的线性二次模型的参数进行了估计,取得较好的拟合效果,并对放射治疗干预下宫颈癌患者病情发展变化情况进行了预测。WATANABE等[13]将肿瘤细胞分成增殖细胞和非分裂细胞,建立了放射治疗干预下的肿瘤生长两仓室模型,并考虑了血管对肿瘤生长的影响,该模型较好地模拟老鼠实验数据。
基于处于休眠状态的宫颈癌细胞的放射不敏感性和单次放射治疗的时间较短,为了更真实地模拟宫颈癌患者的放射治疗过程,本文将宫颈癌细胞种群分为处于分裂状态、休眠状态和死亡状态的三个细胞子群,用脉冲微分方程去描述在放射治疗干预下宫颈癌细胞数量的动态变化过程,进一步地从理论上探讨不同的放射治疗强度对宫颈癌放射治疗效果的影响,以期能够为临床医疗工作者在宫颈癌放射治疗方案设计上提供理论参考。
1 模型的建立
把宫颈癌细胞种群分为处于分裂状态、休眠状态和死亡状态三个子群,它们各自的细胞数量分别用x、y和z来表示。基于宫颈癌细胞的分裂机制,假设:
(1)在缺乏治疗的情况下,增殖的宫颈癌细胞生长曲线满足Logistic方程;
(2)处于增殖状态的宫颈癌细胞可以转化为休眠状态;
(3)处于休眠状态的宫颈癌细胞也可以转化为分裂状态或者死亡。
再则,单次放射治疗相对于整个治疗过程是短暂的,因此使用脉冲微分方程能够更好地描述宫颈癌的放射治疗过程。具体的宫颈癌放射治疗模型如下:
(2)
其中:r为增殖宫颈癌细胞的最大增长率;k为增殖宫颈癌细胞的系统容量;a为增殖细胞到休眠细胞的转化率;b为休眠的宫颈癌细胞向增殖的宫颈癌细胞的转化率;δ为休眠的宫颈癌细胞的死亡率;u为死亡状态细胞的去除率;s为采用剂量为d的单次放射治疗后,处于增殖状态的宫颈癌细胞的存活比例,具体的表达式如模型(1)所示;τ为相邻两次放射治疗的时间间隔;n=1,2,…;
由于肿瘤微环境多种因素的调节作用,增殖状态的宫颈癌细胞向休眠状态转化的过程是极其复杂的,这里采用双线性转移形式axy来表示。
2 模型的基本性质
从系统(2)可以看出,前两个方程中不含z,因此考虑系统(2)的子系统:
(3)
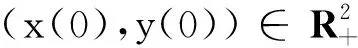
证明令v=x+y,则有
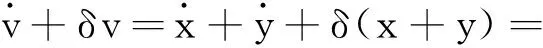
因此,可得
考虑如下系统
(4)
易得系统(4)的解为
进而有
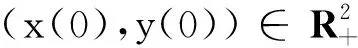
在缺乏休眠的宫颈癌细胞(y=0)的情况下,系统(3)变为
(5)
在区间(nτ,(n+1)τ]上积分系统(5),可得
则有
x((n+1)τ+)=
(6)
显然,差分方程(6)存在一个平凡的不动点x0=0和一个正不动点x1,
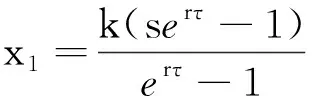
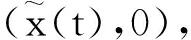
为了便于下面探讨平凡平衡点和边界周期解的稳定性,定义两个阈值:
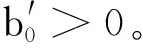
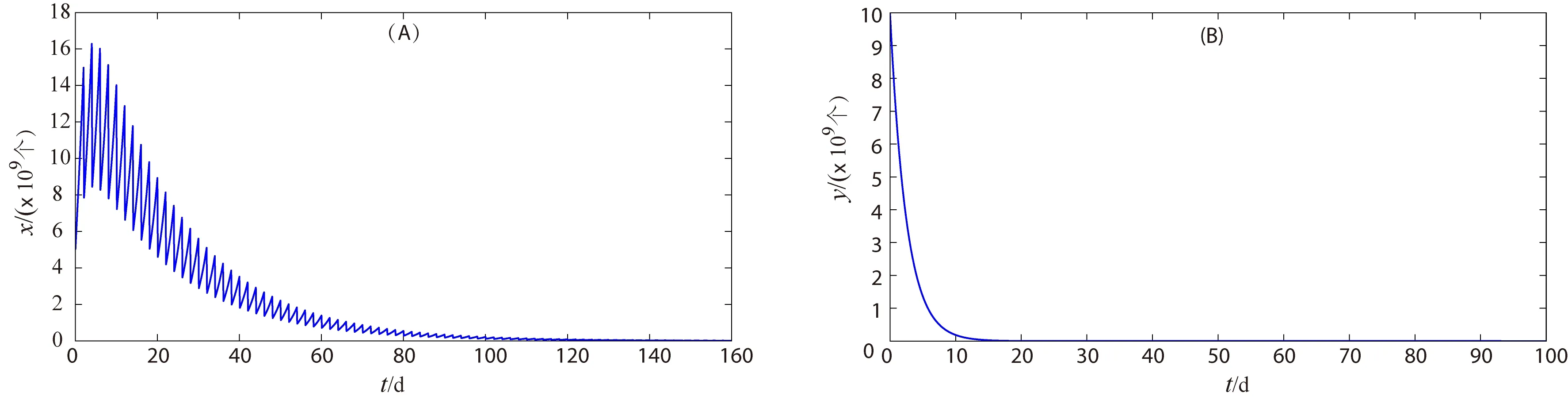
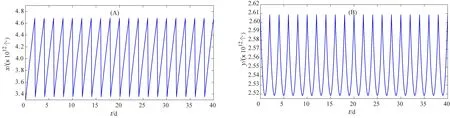
定理1 当s 证明当s F(x(nτ+))=x((n+1)τ+)= 由于 因此系统(3)的平凡平衡点是渐近稳定的。证毕。 证明定义 或写为 矩阵A(t)=(aij(t))(i,j=1,2)满足 A(0)=E, 其中E为单位矩阵。系统(3)的第三、第四个方程变为 如果单值矩阵 其中: exp(rτ-2ln(serτ))=s-2exp(-rτ), 则A的特征值 可知当s0 下面利用ABDELKADER和ARINO的分支理论[14],讨论系统(3)正周期解的存在性。考虑系统(3),则有 (7) 1-exp(rτ0-2ln(serτ))= 因为 bτ0-(b+δ)τ0=-δτ0<0, 因此可以判定 容易验证 因此必有 进一步可得B<0和BC<0,从而有下面的定理。 定理3 当s>s1且s接近s1时,系统(3)存在一个超临界分支,即存在一个稳定的正周期解。 取参数r=0.3,k=2.0×1013,τ=2.0,b=0.3,δ=0.1和a=1.0×10-13,因此可以得到两个阈值的值分别为s0=0.548 8和s1=0.618 8。 (1)当s=0.5 图1 当s (2)当s=0.6∈(s0,s1)时,增殖的宫颈癌细胞和休眠的宫颈癌细胞数量随时间动态变化过程如图2所示。从图2可以看出,当单次放射治疗宫颈癌细胞的存活率大于阈值s0而低于阈值s1时,增殖的宫颈癌细胞将呈现周期性振荡,而休眠的宫颈癌细胞将最终被消除,这与定理2的结论是一致的。 图2 当s∈(s0,s1)时,增殖的宫颈癌细胞和休眠的宫颈癌细胞数量的时间序列图Fig. 2 Time series of proliferating cervical cancer cells and dormant cervical cancer cells for s∈(s0,s1) (3)当s=0.7>s1时,增殖的宫颈癌细胞和休眠的宫颈癌细胞数量随时间动态变化过程如图3所示。从图3可以看出,当单次放射治疗宫颈癌细胞的存活率大于阈值s1时,增殖的宫颈癌细胞和休眠的宫颈癌细胞的数量均呈现周期性振荡,其与定理3的结论是一致的。 图3 当s>s0时,增殖的宫颈癌细胞和休眠的宫颈癌细胞数量的时间序列图Fig. 3 Time series of proliferating cervical cancer cells and dormant cervical cancer cells for s>s1 从理论分析和数值模拟的结果可以发现,增殖的宫颈癌细胞对放射治疗的敏感性的强弱决定了放射治疗的效果。敏感性越强(即单次放射治疗后宫颈癌的存活率越低)宫颈癌越容易成功治疗(对应定理1和图1),而放射敏感性越弱则治疗效果越差(对应定理3和图3)。因此,提高放射敏感性是今后提高放射治疗效果努力的方向。 本文仅仅从理论和数值模拟上探讨了放射敏感性对放射治疗效果的影响,下一步将结合模型(1)进一步探讨放射剂量和放射周期对放射治疗效果的影响,进而考虑如何选择合理的放射剂剂量和相邻两次放射治疗的时间间隔,使得放射治疗的效果达到更好的治疗效果。最好能够结合不同宫颈癌患者放射治疗过程中的临床数据,对模型的参数进行估计,从患者的特异性参数值上探讨宫颈癌患者的相似性和差异性,挖掘放射治疗患者的特征信息,为新增的宫颈癌患者采取个性化的放射治疗方案提供理论支撑。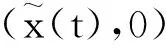

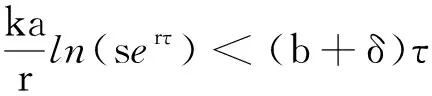
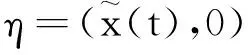

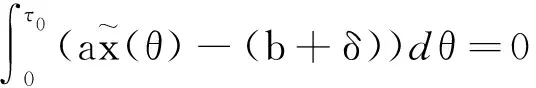
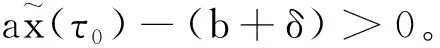
3 数值模拟

4 结论与讨论
