基于多尺度均值排列熵和参数优化支持向量机的轴承故障诊断
2022-01-27王贡献胡志辉赵博琨
王贡献, 张 淼, 胡志辉, 向 磊, 赵博琨
(武汉理工大学 物流工程学院,武汉 430063)
滚动轴承是广泛应用于旋转机械的易损重要零部件,其运行状态直接影响机械设备工作效率和安全性[1]。因此,对滚动轴承运行状态进行监测与诊断,尤其是滚动轴承早期故障诊断具有重要意义[2]。
由于滚动轴承自身非线性刚度和轴承间隙等因素,其运行产生的振动信号经常表现出非平稳和非线性[3]。因此,实现从非平稳和非线性信号中提取有用故障特征信息是滚动轴承故障诊断的重点和难点。基于熵的方法可以识别非线性参数,如近似熵[4]、排列熵[5]、模糊熵[6]和多尺度熵[7],其中,Christoph等[8]提出的排列熵(permutation entropy, PE)无需考虑时间序列的数值大小,而是对相邻样本点进行对比分析,获取相应特征信息,用于检测时间序列随机性和动力学突变,具有计算简单、抗噪能力强和计算速度快等优点,故被广泛用于故障诊断[9]。PE与信号处理方法结合能够提取时间序列特征信息,如局部特征尺度分解[10]、集合经验模态分解[11]和变分模态分解[12]。然而,PE算法仅考虑单一尺度下时间序列数据信息,特征提取能力不足。为此,Aziz等[13]结合PE与多尺度熵提出了多尺度排列熵(multiscale permutation entropy, MPE)。郑近德等[14]将MPE与SVM结合用于滚动轴承故障诊断,取得较高的故障识别准确率,证明了MPE能够有效提取时间序列特征信息。然而,MPE仍存在以下缺陷,一方面,对时间序列粗粒化处理会导致粗粒化序列长度变短,当粗粒化尺度较大时不可避免地容易丢失原始信息,并且熵值的估计偏差会随着尺度增大而增大;另一方面,粗粒化过程将一个时间序列分割为等长的非重叠的片段再计算每一个片段内所有数据点的均值,这种均值化处理会一定程度上中和原始信号的动力学突变行为。
在充分提取振动信号故障特征信息基础上,滚动轴承故障诊断的关键是利用特征信息实现故障模式识别。支持向量机(support vector machine, SVM)在小样本、低维度数据分类上具有速度快、准确率高的优点,故被广泛用于故障诊断领域,然而SVM性能容易受到惩罚因子c和核函数参数g影响。为此,有学者将网格寻优算法[15]、遗传算法[16]、粒子群优化算法[17]和模拟退火算法[18]等用于SVM参数寻优,但这些方法存在寻优耗时长和容易陷入局部最优解等问题。灰狼算法[19](grey wolf optimization,GWO)具有参数简单、全局搜索能力强、收敛速度快和易于实现等优点,将其用于SVM超参数选择,可以提高分类精度。宋宣毅等[20]利用GWO-SVM实现了油井初期产能预测。Dong等[21]将时移多尺度加权排列熵与GWO-SVM结合用于轴承故障诊断。上述方法均具有较好的实用性。
针对MPE的不足,将多尺度均值化代替粗粒化方法,提出了一种多尺度均值排列熵算法(multiscale mean permutation entropy, MMPE),旨在更加充分提取时间序列有用特征信息。在此基础上,采用GWO-SVM多分类器进行故障模式识别,并建立一种基于MMPE和GWO-SVM的滚动轴承故障诊断模型,通过提取原始时间序列的MMPE特征信息构成特征数据集,用训练集训练GWO-SVM,在测试集进行故障模式识别,将其应用于滚动轴承试验数据,可为滚动轴承故障诊断提供理论参考。
1 多尺度均值排列熵
1.1 多尺度排列熵
MPE考虑多个尺度下时间序列顺序结构特征,能够充分提取信号特征信息,具体算法如下:
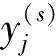
(1)
式中:[N/s]为对N/s取整数;s为正整数尺度因子。当s=1时,粗粒化序列即为原始序列;当s=2,3,…时,原始系列变为长度为[N/s]的粗粒化序列。
分别计算尺度1~s的粗粒化序列PE值,构成原始序列s尺度MPE。
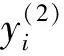
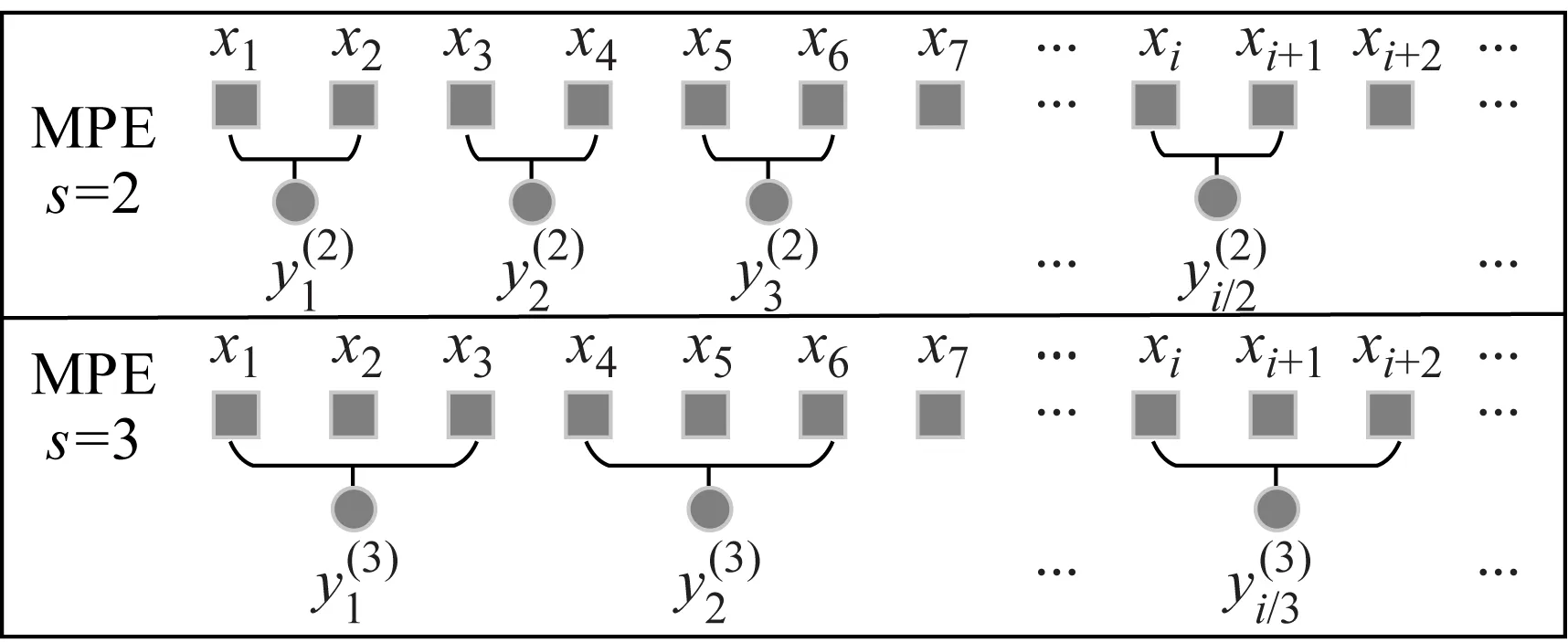
图1 MPE粗粒化构造方式(s=2和3)Fig.1 Coarse grained structure of MPE(s=2 and 3)
1.2 多尺度均值排列熵
针对MPE存在的不足,同时考虑到对相同连续信号进行离散采样,不同采样频率和采样起点所得时间序列不同,造成其PE值不同。为此,提出多尺度均值排列熵(multiscale mean permutation entropy, MMPE),旨在保留更多的数据信息、减少信号采样误差和扩充样本,具体算法原理如下:
(2)
当s=1时,均值化序列即为原始序列;当s=2,3,…时,原始序列变为长度为(N+1-s)的均值化序列。
分别计算尺度1到s的均值化序列PE值,构成原始序列s尺度MMPE。
MMPE时间序列均值化方式如图2所示,其实质是在时间序列上加宽度为s、步长为1的滑动窗口,每个窗口内部取均值得到均值化序列,均值化过程除首尾几个点外,每个数据点重复使用s次,充分提取原始数据信息。以s=3为例,长度为N的时间序列x(i)进行均值化处理后得到长度为(N-2)的新序列,计算尺度1、2和3均值化序列排列熵值PE1、PE2和PE3,构成的3维向量即时间序列3尺度MMPE。
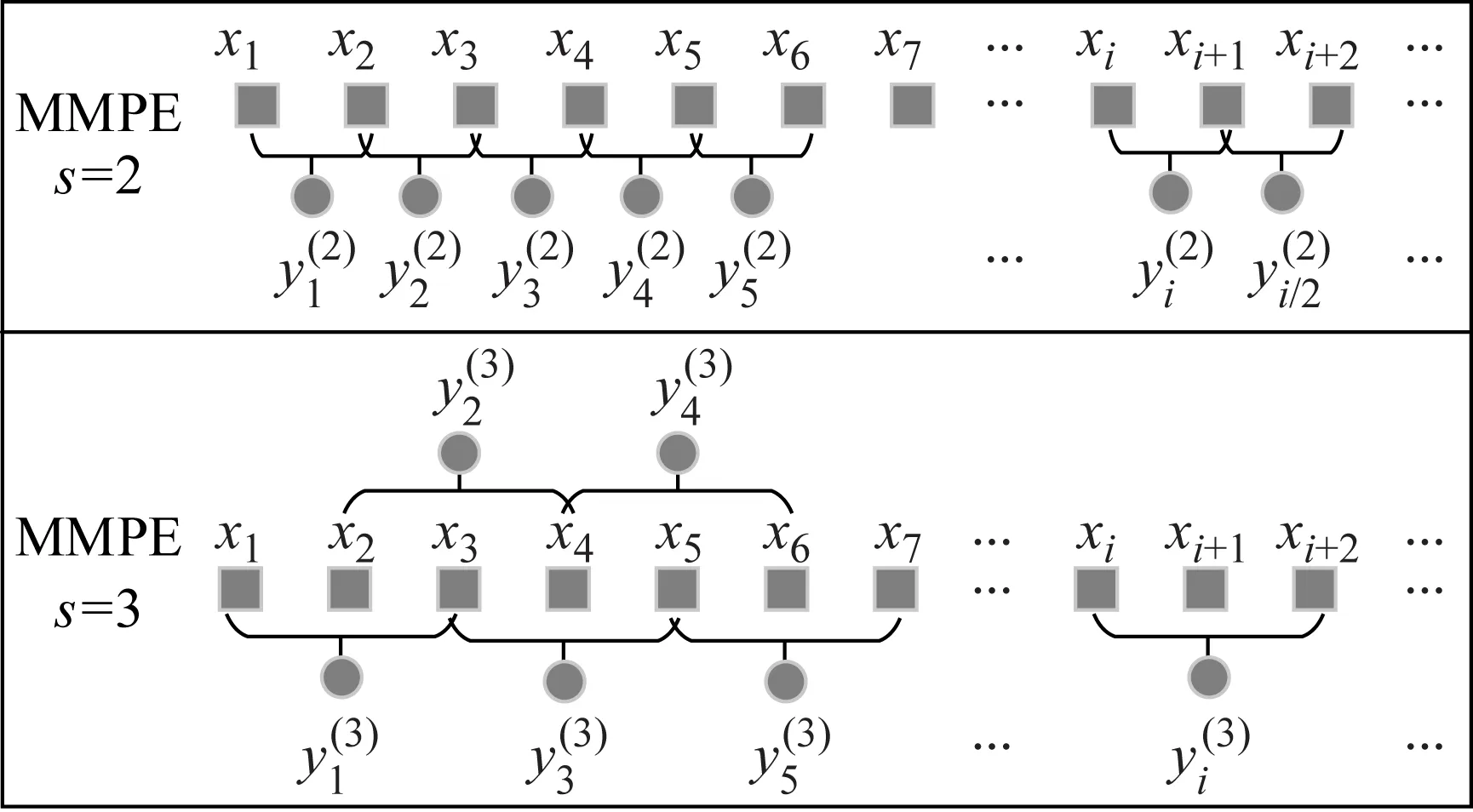
图2 MMPE均值化构造方式(s=2和3)Fig.2 The mean structure of MMPE(s=2 and 3)
2 灰狼优化支持向量机
2.1 灰狼算法
灰狼算法(grey wolf optimization, GWO)是一种模拟狼群等级制度和分工狩猎行为的新型群体智能优化算法。GWO中狼群根据社会等级依次记为头狼α、β狼、σ狼和ω狼。捕猎过程中将每只狼作为潜在捕猎方案,α、β和σ依次作为第一、第二和第三最优解,狼群根据猎物信息不断调整移动,狩猎过程包括:追踪、包围和攻击猎物。
(1) 追踪和包围猎物,狼群根据与猎物间的距离不断调整自身位置,其数学描述如下
D=|CXp(t)-X(t)|
(3)
X(t+1)=Xp(t)-AD
(4)
式中:D是灰狼与猎物间距离;Xp(t)为猎物当前位置;t为迭代次数;X(t)为灰狼当前位置;A和C是系数矩阵。A和C可表示如下
A=2ar1-a
(5)
C=2ar2
(6)
当|A|>1时,狼群将扩大搜索范围,以寻找更好的猎物。相反,当|A|≤1时,狼群将缩小包围圈并搜寻附近的猎物。r1,r2为[0,1]间随机值;a为收敛因子,随着迭代次数增加从2线性递减到0。
(2) 靠拢并攻击猎物,狼群寻找到猎物大致方位后,将靠拢并对猎物发起攻击,这种行为数学描述为
(7)
(8)
X(t+1)=(X1+X2+X3)/3
(9)
式中:Xα(t)、Xβ(t)、Xσ(t)分别为α、β和σ的当前位置;Dα、Dβ和Dσ分别为α、β和σ与猎物之间的距离;X1、X2和X3代表α、β和σ指导ω下一步移动的方向向量,狼群下一步移动的方向向量由式(9)决定。
2.2 灰狼优化支持向量机
支持向量机(SVM)因其优异的分类性能和可靠性被广泛用于故障诊断领域,然而SVM性能易受惩罚因子c和核函数参数g的影响。GWO具有参数简单、全局搜索能力强、收敛速度快和易于实现等优点,将其用于SVM超参数选择,可以提高分类精度。GWO-SVM流程如图3所示,具体过程如下:
步骤1 输入训练数据和测试数据,初始化GWO参数,设定种群规模p、最大迭代次数t0和搜索空间维度T,在设定范围内随机生成狼群位置。
步骤2 初始化SVM参数,设置c和g的搜索范围,以SVM识别准确率作为适应度函数。
步骤3 计算当前位置狼群的适应度函数值,通过式(7)和(8)不断更新狼群位置和适应度函数值。
步骤4 判断迭代次数,当迭代次数不超过设定最大值时返回步骤3,否则,寻优结束,输出最佳参数c和g。
步骤5 使用最佳参数c和g开始训练SVM,用训练好的模型在测试集上进行故障分类。
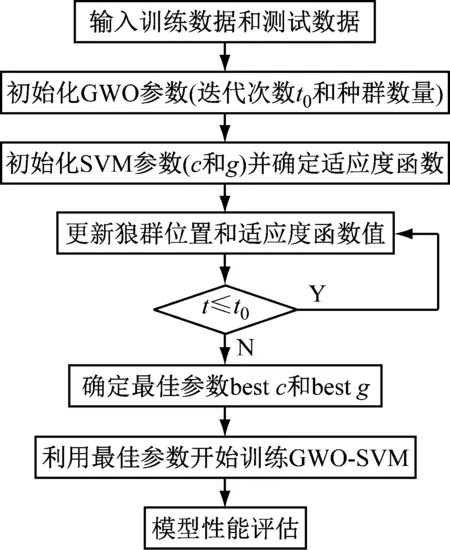
图3 GWO-SVM流程图Fig.3 The flowchart of GWO-SVM
3 故障诊断模型
为实现滚动轴承故障诊断,在得到原始振动信号MMPE并构成特征数据集后,采用GWO-SVM多分类器进行故障模式识别。基于MMPE和GWO-SVM的故障诊断方法流程如图4所示,具体步骤如下:
步骤1 假定滚动轴承有k种状态类型,每种类型采集i组样本,根据信号数据分析确定MMPE参数,包括样本长度N、嵌入维数m、尺度因子s和时延λ。
步骤2 计算每个样本MMPE值作为输入特征向量。
步骤3 将MMPE计算结果汇总,根据故障类型设置1~k标签,每种类型选取j个样本作为训练样本,剩余样本作为测试样本,分别构成训练样本特征集和测试样本特征集。
步骤4 采用训练样本特征集对GWO-SVM多分类器进行训练,灰狼算法自动选取最佳参数c和g。
步骤5 用训练好的GWO-SVM多分类器对测试样本特征集进行故障类型和故障程度识别。
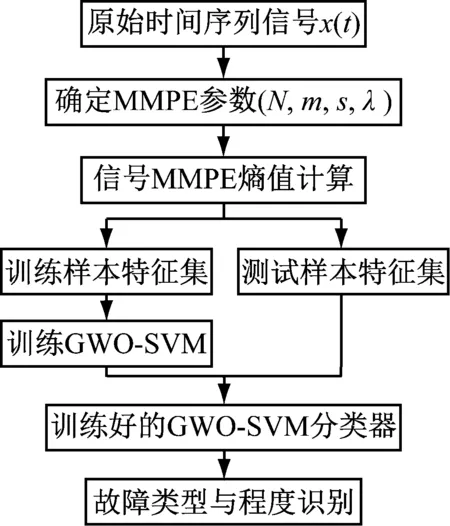
图4 故障诊断模型流程图Fig.4 The flowchart of fault diagnosis model
4 滚动轴承故障诊断试验研究
4.1 试验数据
为验证MMPE和GWO-SVM方法对轴承故障诊断的有效性,将其应用于凯斯西储大学轴承数据进行试验分析。试验采用6205-2RS型深沟球轴承,利用电火花技术分别在轴承外圈、内圈和滚动体上进行单点故障加工,故障直径分别为0.177 8 mm、0.355 6 mm和0.533 4 mm,故障深度为0.279 4 mm,电机载荷为3马力,试验电机转速为1 730 r/min,在12 kHz采样频率下采集到正常(normal, NOR),外圈故障(outer race fault, ORF),内圈故障(inner race fault, IRF)和滚动体故障(ball fault, BF)四种状态的振动信号。
为进行故障位置和故障程度识别试验,将每种故障轴承信号按故障直径大小分为轻微、中度和严重三种故障程度,总计得到10种状态的信号(对应标签为1~10),分别记为正常NOR、内圈轻微故障IRF1、外圈轻微故障ORF1、滚动体轻微故障BF1、内圈中度故障IRF2、外圈中度故障ORF2、滚动体中度故障BF2、内圈严重故障IRF3、外圈严重故障ORF3、滚动体严重故障BF3,每种状态取50个样本,每个样本含2048个数据点。各种状态的轴承信号数据信息如表1所示,其时域波形如图5所示。
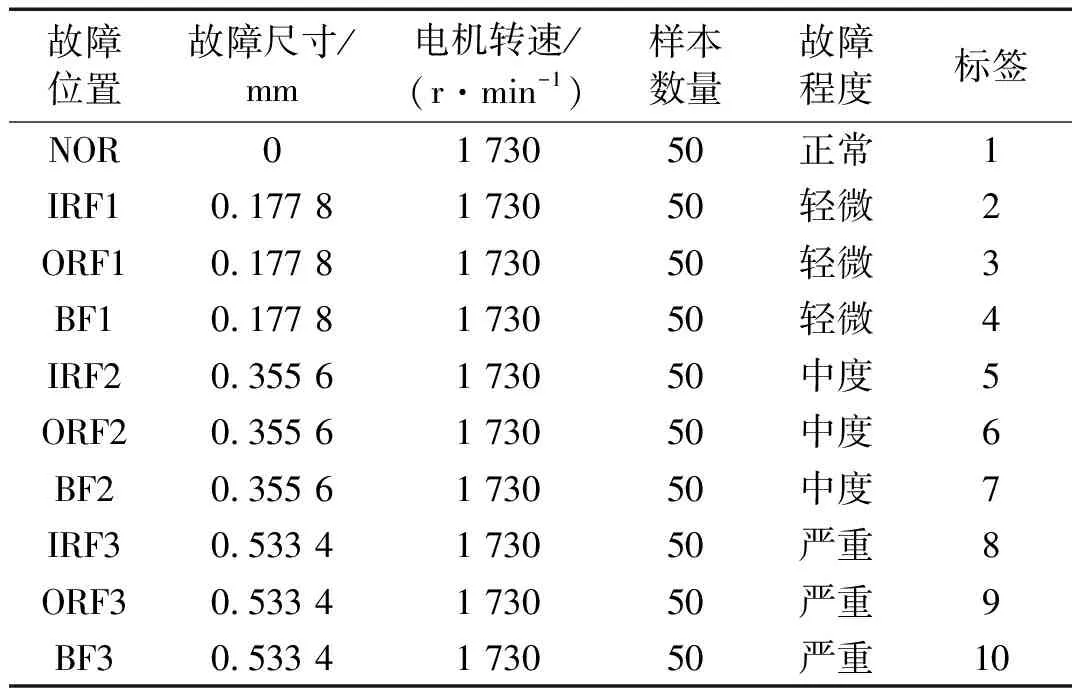
表1 轴承数据信息
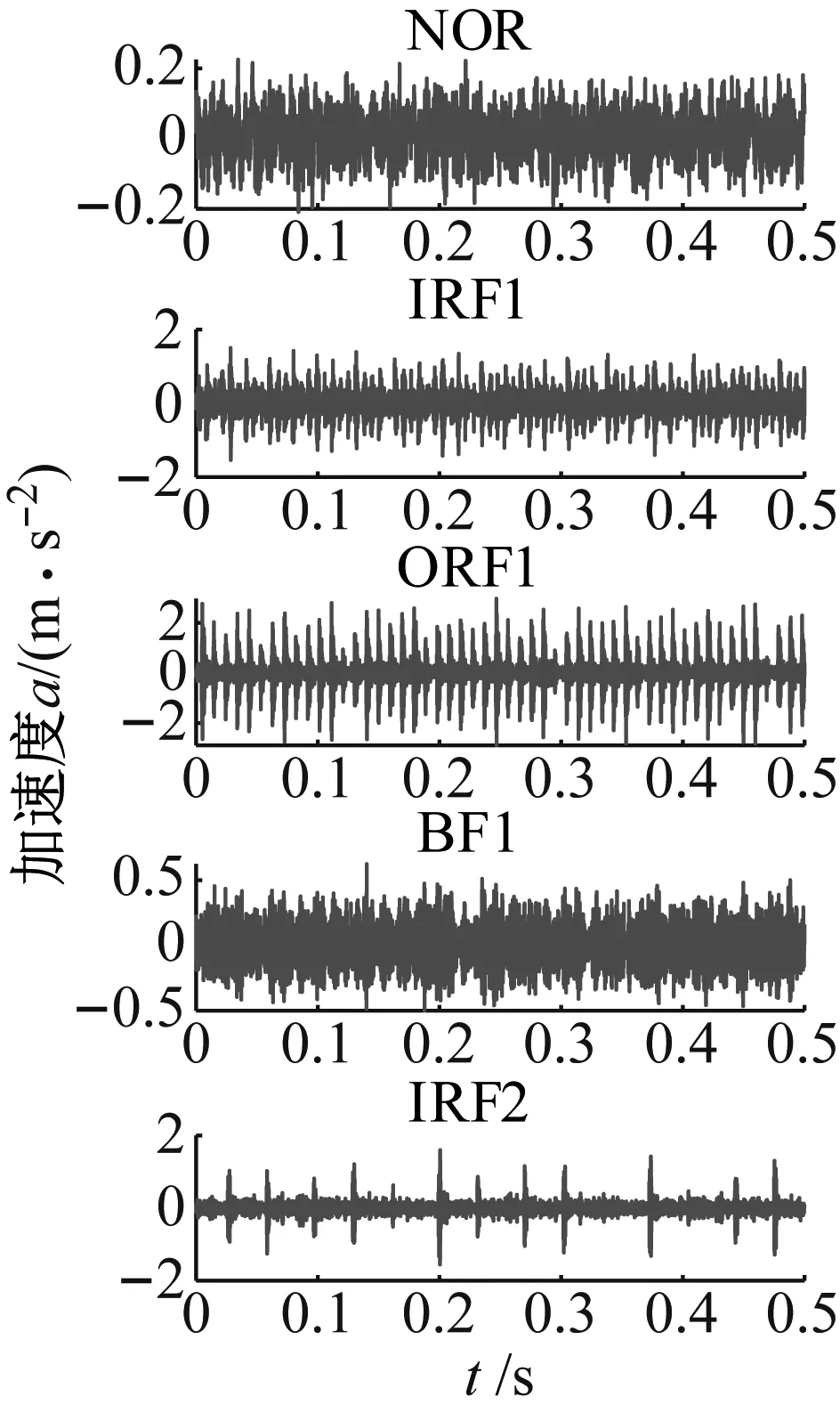
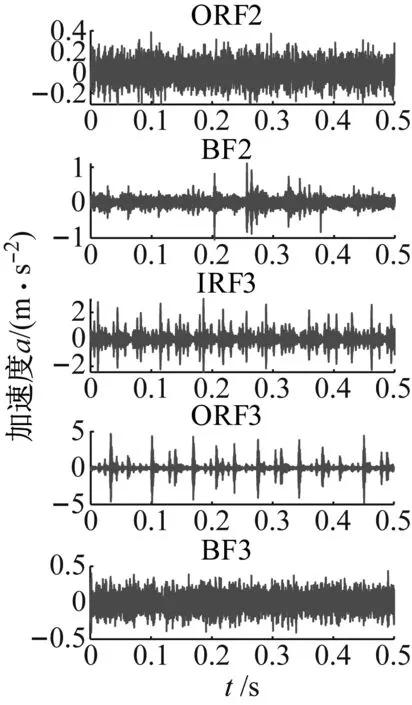
图5 轴承信号时域波形Fig.5 Time domain waveforms of bearing signal
4.2 MMPE参数选择和分析
MMPE具有4个关键参数,分别为样本长度N、尺度因子s、时延λ和嵌入维数m。MMPE算法基本不会改变数据长度,因此对N取值不敏感,而MPE的粗粒化处理时,s越大则需要N越大;s取值没有固定要求,一般s大于10即可。为对比MMPE与MPE的特征提取能力,参照文献[14]中MPE参数取值,N、s分别设置为2 048和12。λ对熵值影响较小,一般设定为1。m的选择对MPE和MMPE具有较大影响,m过小,相空间重构向量信息不足,无法有效监测序列动力学突变;反之,m过大,相空间重构向量忽略序列细微变化,并且会增加运算时间,通常m的取值4~7之间。
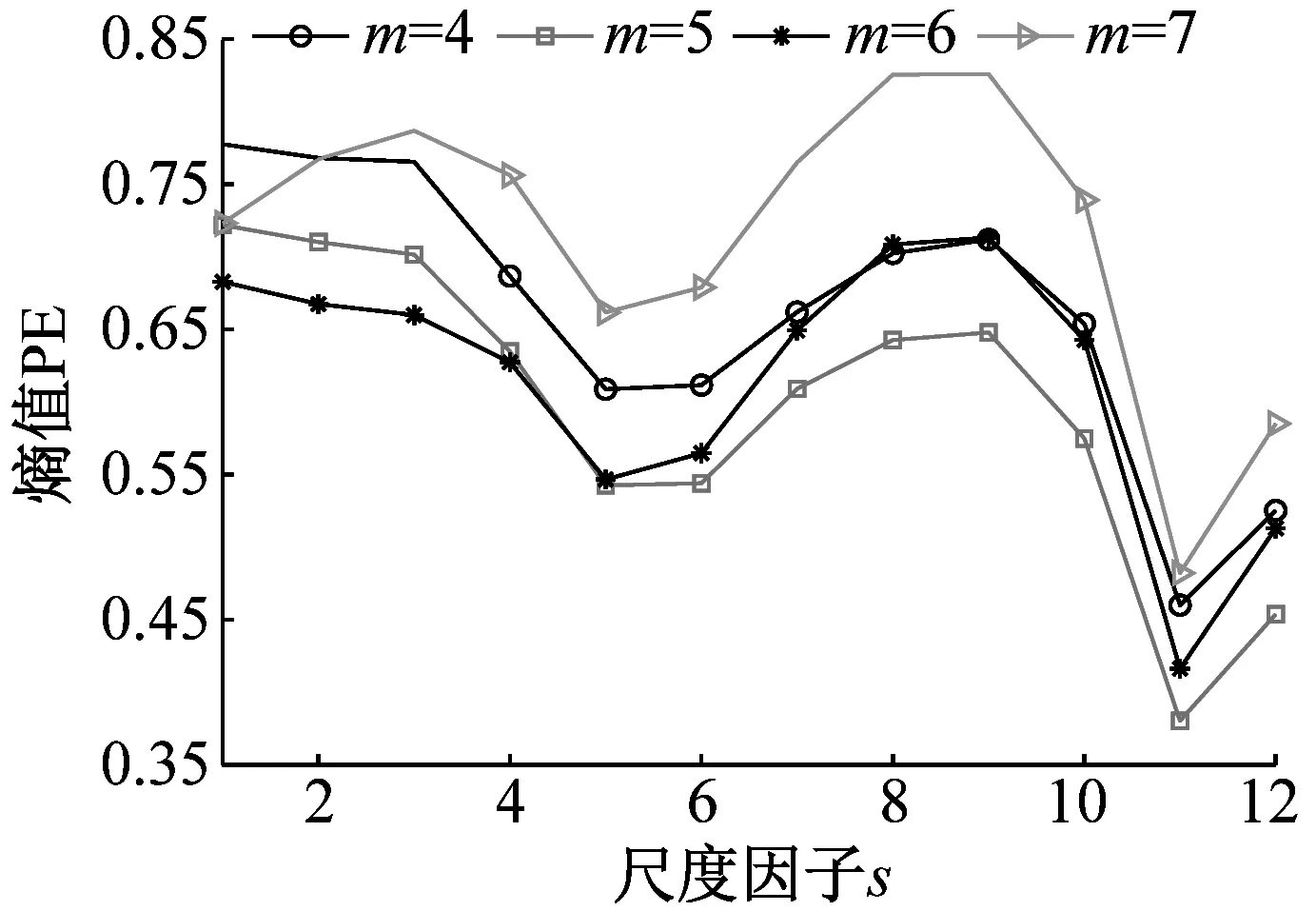
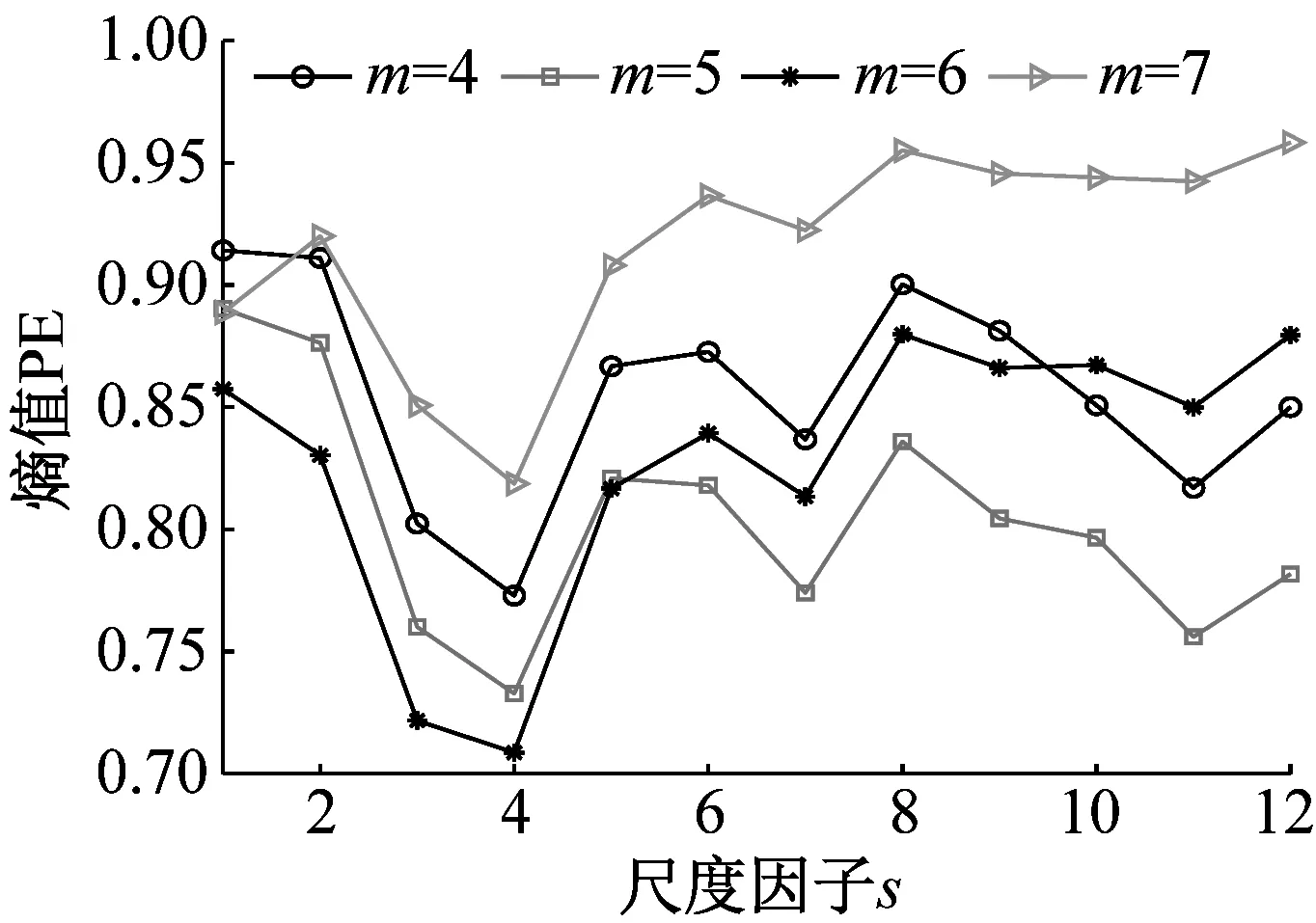
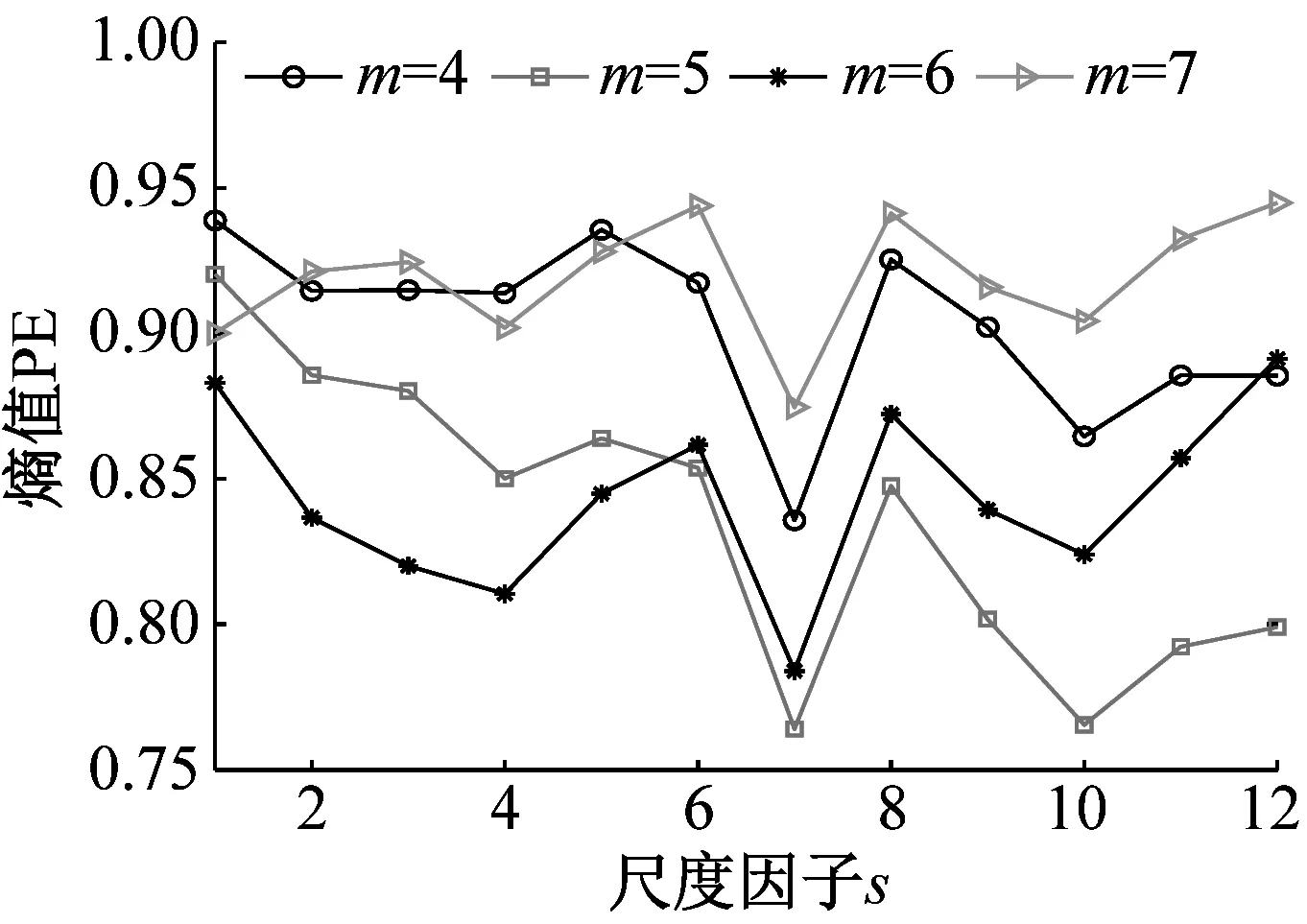
为探究嵌入维数m对时间序列MMPE的影响,分别从NOR、IRF、ORF和BF信号中随机选取一组样本数据,m分别设置为4、5、6、7,计算其MMPE。四组样本信号MMPE结果如图6所示。
(a) 正常信号
(b) 内圈故障信号
(c) 外圈故障信号
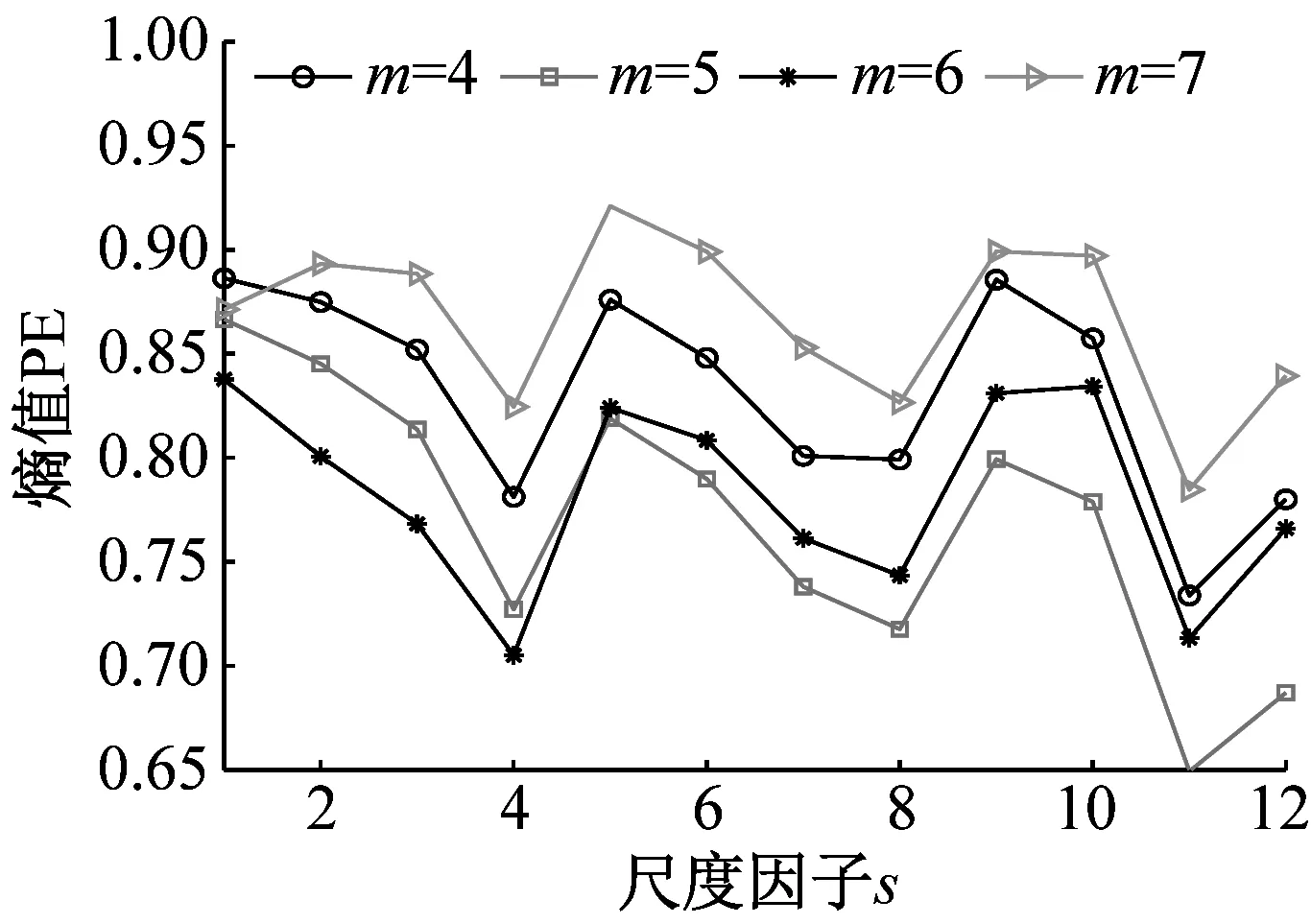
(d) 滚动体故障信号图6 不同m下,MMPE对不同信号分析结果Fig.6 Analysis results of different signals by MMPE with different m
分析图6可知:(1)当s小于4时,PE值随着s增加而减小,表明了在s较小时均值化处理能使时间序列更加平稳规则;当s大于4时,PE值没有明显的规律性,不能表征轴承状态,并且SVM适合处理低维数据,因此选取前4个尺度的熵值作为特征向量,即T=(PE1,PE2,PE3,PE4);(2)当m=6时,四种状态轴承信号前4个尺度的PE值较小,其MMPE能够更好的表征信号状态信息,因此试验时m设置为6。
10种轴承状态各随机选取一组数据,其MMPE如图7所示,正常状态轴承信号排列熵较小,其前四个尺度PE值均小于0.7,符合正常状态轴承信号冲击性小、平稳性高的振动特性;各故障信号的MMPE均较大,并且对于同种故障,故障尺寸不同其排列熵值也明显不同,表明MMPE理论上能够表征轴承振动信号状态信息,可作为模式识别分类器的输入。
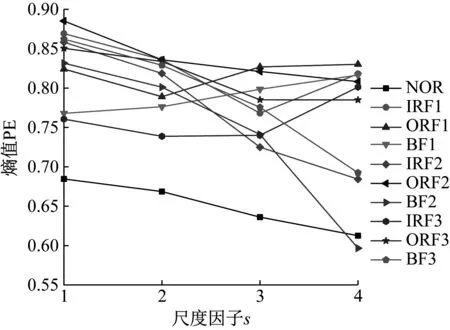
图7 不同状态轴承信号的MMPEFig.7 MMPE of bearing signals in different states
4.3 参数优化SVM试验研究
从每种轴承状态数据50组样本中各选取30组作为训练集,剩余20组作为测试集,构成300×5的训练数据集和200×5的测试数据集,数据集的前4维是信号前4个尺度的PE特征值,最后1维为标签。GWO参数设置:狼群数量为10,最大迭代次数为100,惩罚因子c取值范围[0.01,100],核函数参数g取值范围[0.01,100]。SVM核函数选择径向基函数,利用MMPE训练集训练GWO-SVM,并在测试集上进行验证。
基于MMPE和GWO-SVM的滚动轴承故障诊断结果如图8所示,前8种状态轴承测试样本分类准确率为100%;外圈严重故障的20个测试样本中2个样本被误判为内圈中度故障;滚动体严重故障的20个测试样本中1个被误判为内圈中度故障,1个被误判为滚动体中度故障。测试集整体识别准确率为98.0%(196/200)。
为了验证GWO-SVM分类器的优越性,将GWO-SVM其他常用优化支持向量机(GS+SVM、GA+SVM、PSO+SVM和SA+SVM)进行试验对比,每种分类器进行五次试验,分别记录故障识别准确率(acc)和训练用时(t),各分类器的对参数c和g的寻优范围均为[0.01,100],其他参数设置如表2所示。
表3为GA-SVM、GA-SVM、PSO-SVM、SA-SVM和GWO-SVM分类结果,对比可知:①MMPE与各种参数优化SVM结合的方法在滚动轴承故障诊断中均取得较高的分类准确率,最低为96.5%。②GS-SVM寻优时间短,但分类准确率(96.5%)较低;GA-SVM训练用时较长,平均分类准确率为97.3%,但每次试验分类准确率不同,表明该方法对初始化参数较为敏感;PSO-SVM,SA-SVM和GWO-SVM三种分类器准确率都为98.0%,但PSO-SVM寻优时间为59.3 s,SA-SVM寻优时间为10.2 s,而GWO-SVM只需要4.6 s即可完成寻优。因此,GWO-SVM在寻优时间和识别准确率上都优于其他方法。
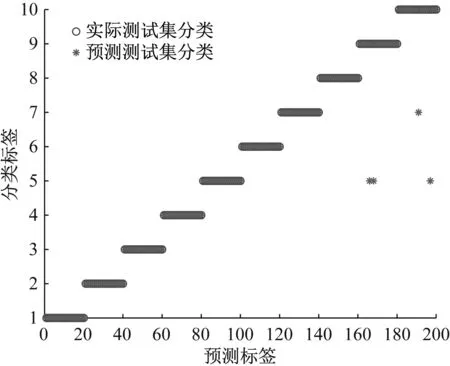
(a) MMPE+GWO-SVM识别结果
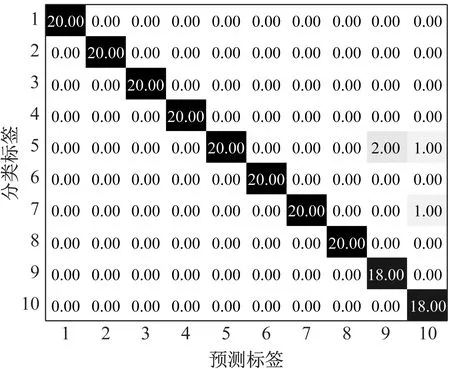
(b) MMPE+GWO-SVM混淆矩阵图8 MMPE+GWO-SVM识别结果和混淆矩阵Fig.8 Recognition results and confusion matrix of MMPE+ GWO-SVM
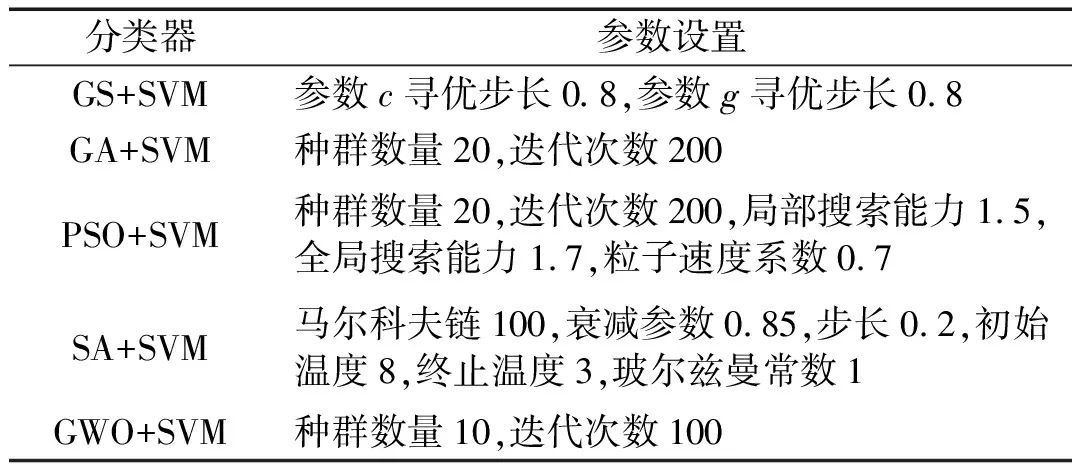
表2 SVM分类器参数Tab.2 Parameters of SVM classifier
4.4 MMPE与MPE特征提取性能对比
为对比分析MMPE和MPE特征提取性能,进行MPE和GWO-SVM轴承故障诊断试验,各参数设置与MMPE和GWO-SVM试验一致。利用MPE训练集训练GWO-SVM,并在测试集上进行验证。
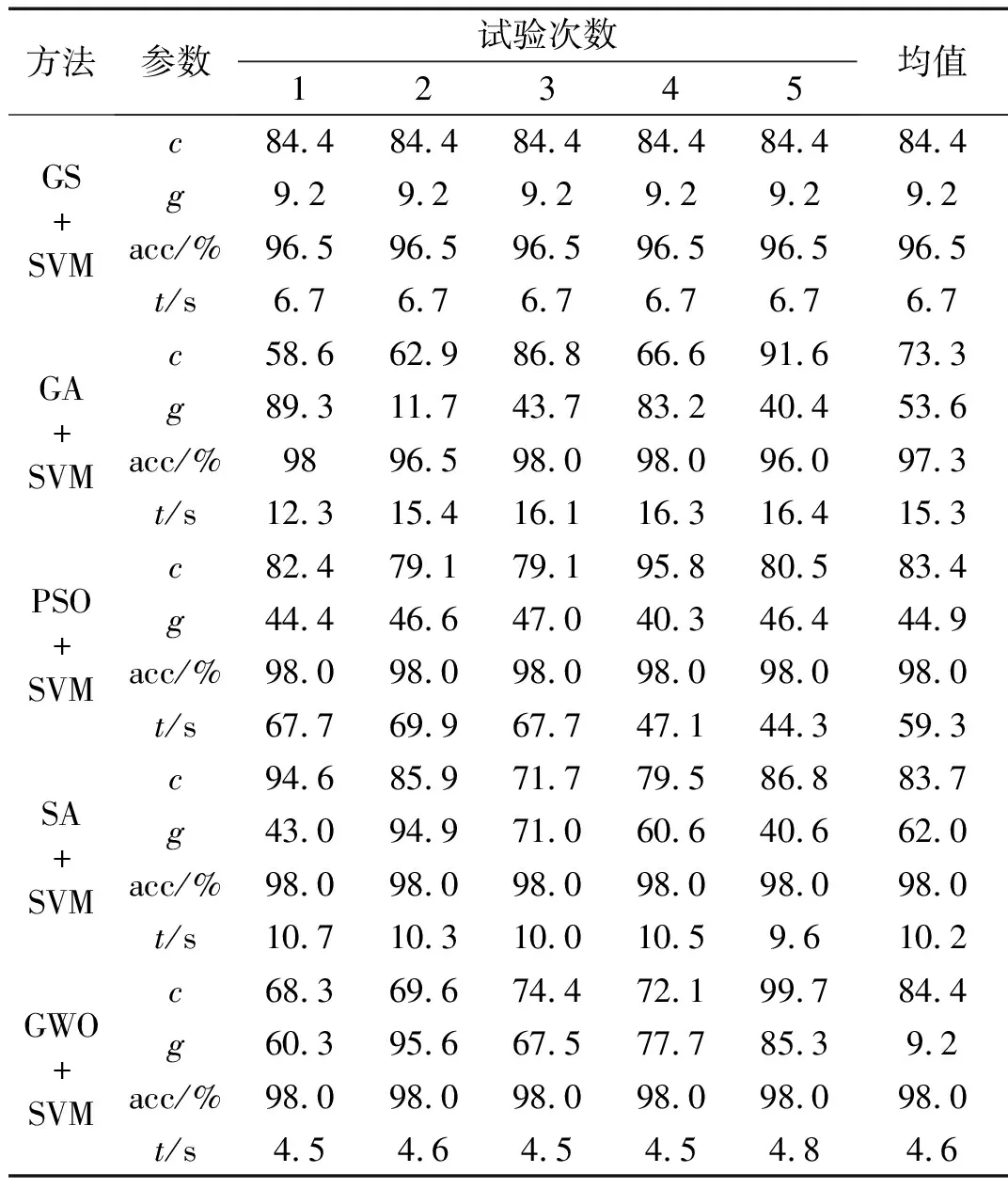
表3 不同分类器识别结果
基于MPE和GWO-SVM的滚动轴承故障诊断结果如图9所示,前6种状态和第8种状态轴承测试样本分类准确率为100%;滚动体中度故障的20个测试样本中1个样本被误判为内圈中度故障;外圈严重故障的20个测试样本中2个被误判为内圈中度故障,2个被误判为滚动体中度故障;滚动体严重故障的20个测试样本中1个样本被误判为内圈严重故障。测试集整体识别准确率为97.0%(194/200),低于本文所提出的MMPE和GWO-SVM方法。
为探究MMPE特征提取的噪声鲁棒性,进行噪声背景下的滚动轴承故障诊断试验。向各组轴承数据添加性噪比为20 dB的高斯白噪声,分别计算其MMPE和MPE,输出数据分别构成MMPE数据集和MPE数据集(试验分组和试验参数与前述试验相同),并建立相同的GWO-SVM模型,分别用两个数据集进行模型训练,通过各自的测试集进行模型评估。
噪声背景下滚动轴承诊断结果如图10所示,加入相同白噪声后,基于MPPE和GWO-SVM方法识别准确率为93.5%(187/200),而基于MPE的GWO-SVM方法识别准确率仅为83.0%(166/200),表明了MMPE和GWO-SVM方法具有更好的噪声鲁棒性。
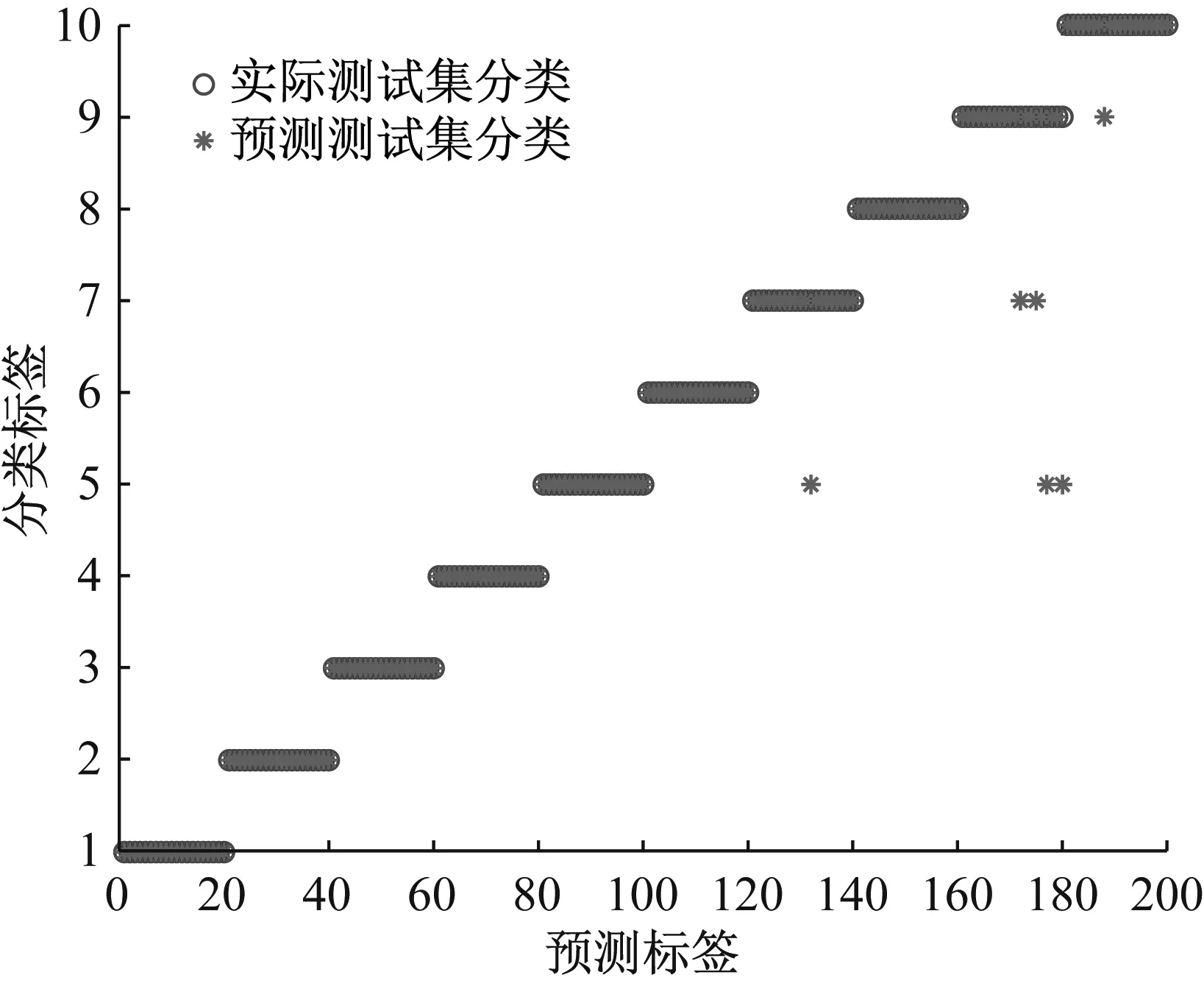
(a) MPE+GWO-SVM识别结果
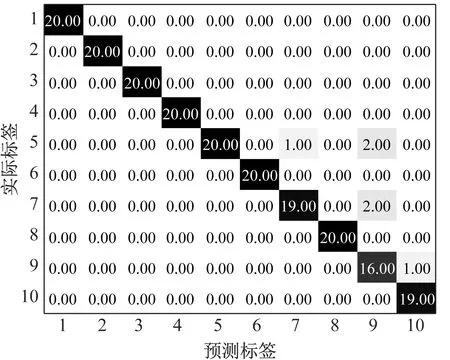
(b) MPE+GWO-SVM混淆矩阵图9 MMPE+GWO-SVM识别结果和混淆矩阵Fig.9 Recognition results and confusion matrix of MPE+GWO-SVM
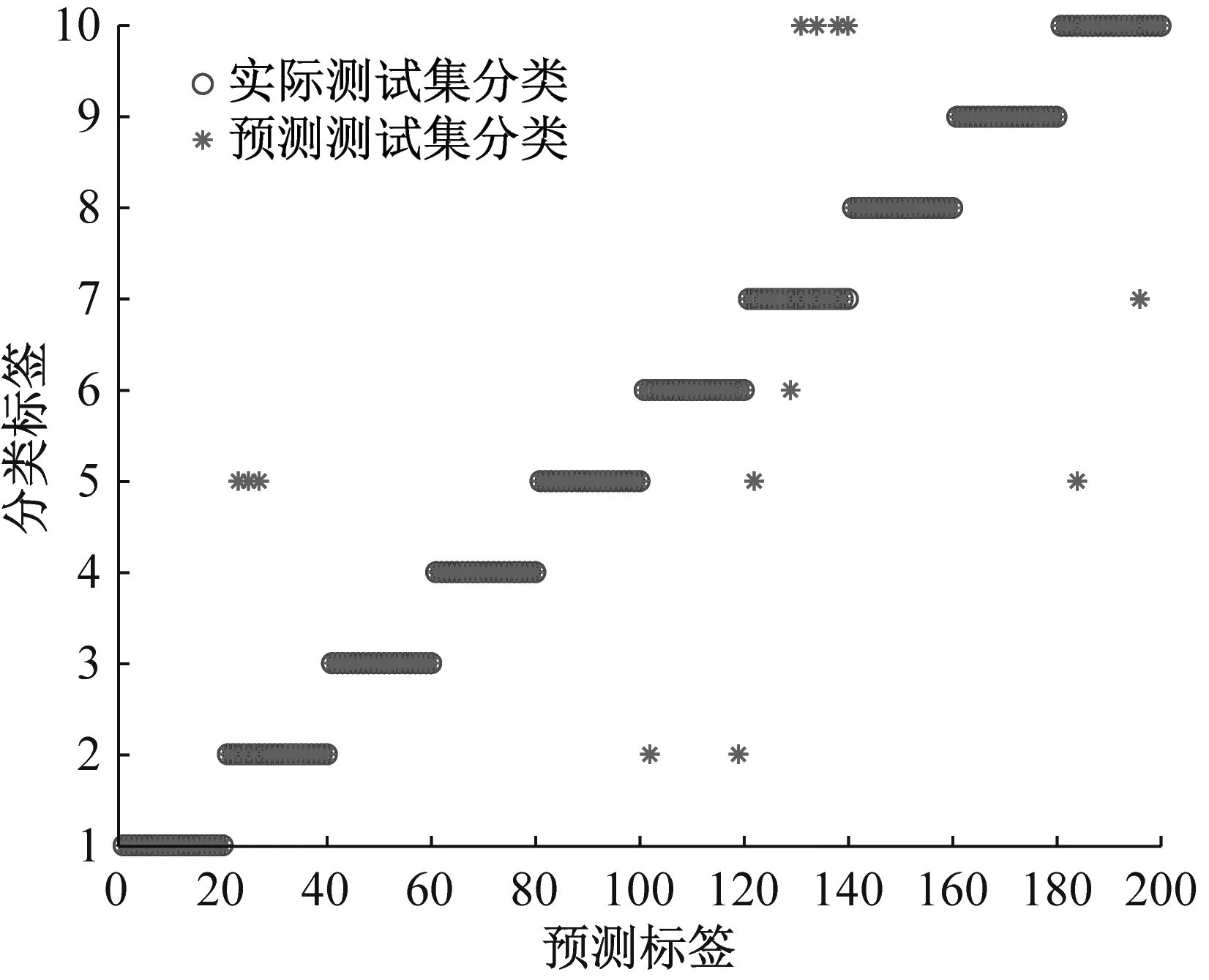
(a) 噪声背景下MMPE+GWO-SVM识别结果
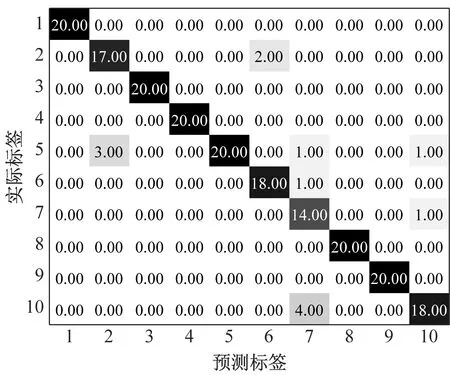
(b) 噪声背景下MMPE+GWO-SVM混淆矩阵
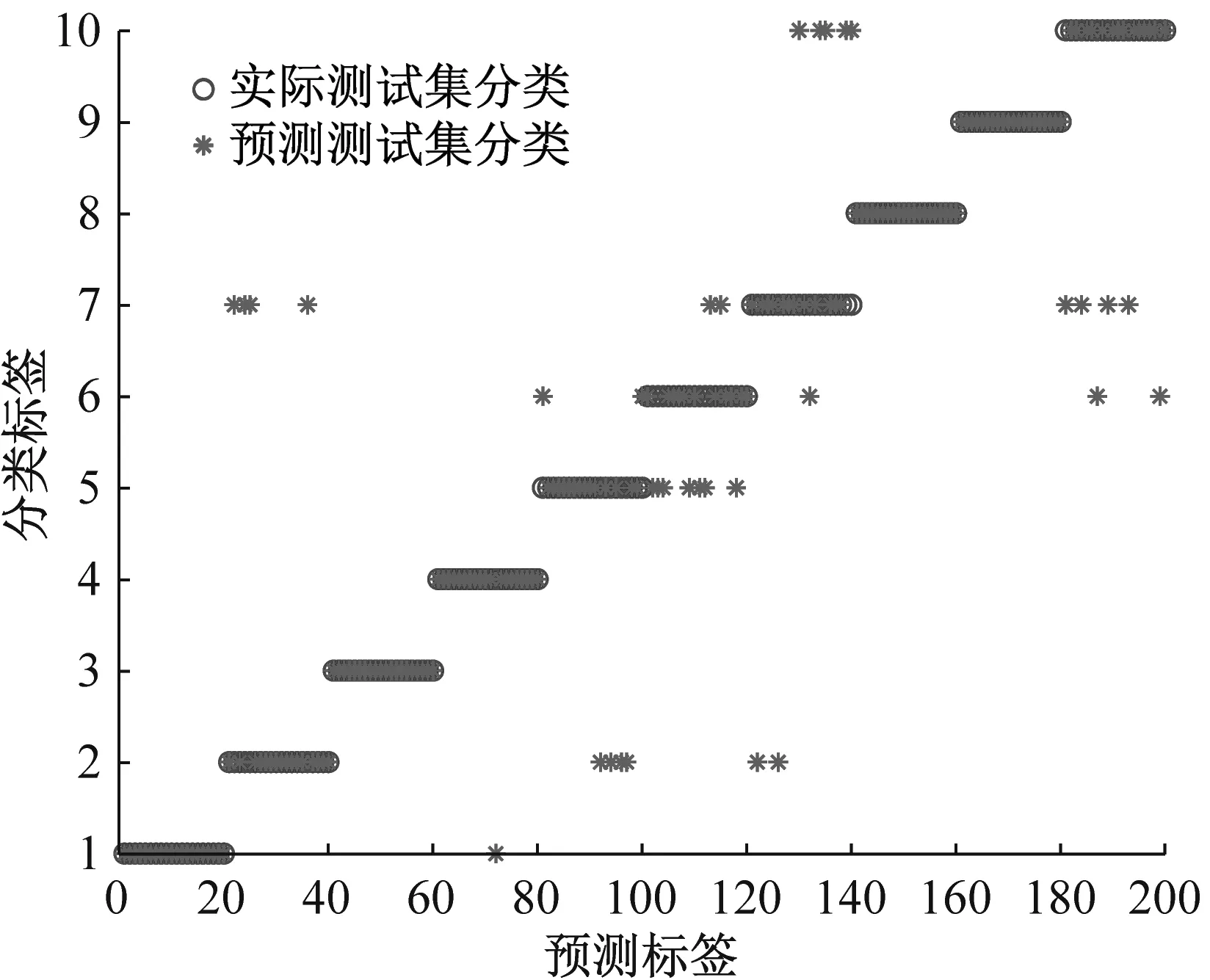
(c) 噪声背景下MPE+GWO-SVM识别结果
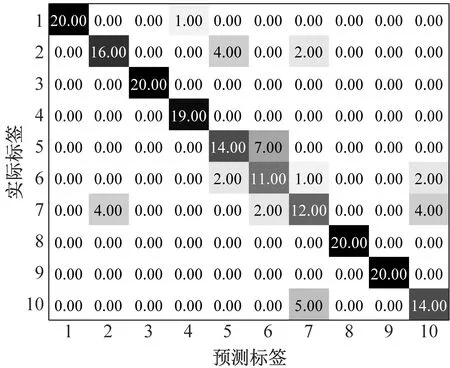
(d) 噪声背景下MPE+GWO-SVM混淆矩阵图10 噪声背景下识别结果和混淆矩阵Fig.10 Recognition results and confusion matrix in noise background
5 结 论
(1) 提出了一种衡量时间序列复杂性的新算法——多尺度均值排列熵MMPE,该算法对原始时间序列进行多尺度均值化处理后计算排列熵,可用于信号特征提取。
(2) 提出了一种基于MMPE和GWO-SVM结合的模式识别方法,滚动轴承故障诊断试验结果表明,GWO-SVM分类器识别准确率和识别速度均优于常用的GS-SVM、GA-SVM、PSO-SVM和SA-SVM。
(3) MMPE和GWO-SVM方法在轴承故障诊断试验上取得98%识别准确率,高于MPE和GWO-SVM方法97%准确率。噪声背景下MMPE和GWO-SVM方法取得93.5%识别准确率,高于MPE和GWO-SVM方法83%准确率,表明MMPE特征提取具有更好的噪声鲁棒性。
