风致飞掷物冲击建筑浮法玻璃试验和数值模拟
2022-01-27陈胜,黄鹏,顾明
陈 胜, 黄 鹏, 顾 明
(同济大学 土木工程防灾国家重点实验室,上海 200092)
大量的风灾灾后实地调查表明,风灾中建筑的破坏形式多是围护结构失效破坏。玻璃门窗等建筑围护结构在风灾中可能受到风压和风致飞掷物冲击双重作用,其中风压荷载为均布荷载,较难直接造成玻璃围护结构的破坏,而风致飞掷物的冲击作用为集中荷载,容易穿透玻璃门窗使其失效。尤其是对低矮建筑而言,其由浮法玻璃构成的门窗等围护结构在风灾中极易遭受风致飞掷物的冲击破坏[1-2]。
在建筑风灾破坏评估中,对风致飞掷物的研究问题可以概括成三类,分别是风致飞掷物的产生及起飞,飞行轨迹,以及对建筑围护结构的冲击效应[3]。现有的研究大部分集中在飞掷物的起飞条件和飞行轨迹[4-6],而对飞掷物的冲击效应关注较少。特别是在判断建筑玻璃是否会破坏时,只是简单地对比风致飞掷物冲击时的动量或者动能与玻璃强度的大小,并未考虑风致飞掷物的外形、冲击姿态等特性对破坏结果的影响。因此,为了准确评价由玻璃构成的门窗等建筑围护结构受风致飞掷物冲击后的破坏概率,进一步完善风灾风险评估系统,有必要对风致飞掷物冲击建筑玻璃的破坏特点进行更深入地研究。
目前,研究玻璃在冲击荷载下破坏的方法主要有理论分析、试验和数值模拟三种。在理论研究方面,研究人员提出了威布尔模型、随机模拟模型、Rankine准则和非局部失效准则等描述玻璃失效的概率模型[7-8],但是这些模型与玻璃的实际破坏情况相差较大。试验是评价玻璃抗冲击性能最可靠的手段,目前世界上大部分规范评估玻璃抗冲击性能的手段都是依赖于特定的试验方法[9-10]。但是,冲击试验需要花费巨大的经济和时间成本,特别是风致飞掷物本身的一些特性,例如飞掷物的外形、飞行速度、冲击姿态和冲击位置等因素都可能影响破坏结果,而用试验的方法研究全部这些因素存在很大的难度,因此需要考虑使用更加高效的数值模拟方法进行风致飞掷物冲击建筑玻璃围护结构的研究。
LS-DYNA是当前最著名的通用显式动力分析程序,特别适合求解各种二维、三维非线性结构的高速碰撞、爆炸和金属成型等非线性动力冲击问题[11-12],目前大部分研究人员均采用其模拟玻璃的碰撞问题。Timmel等[13]提出了利用LS-DYNA模拟夹层玻璃物理模型,将玻璃层当作脆性材料,夹层认为是超弹性材料,着重介绍了超弹性材料夹层的多种本构关系。刘奇等[14]采用LS-DYNA对汽车挡风夹层玻璃受冲击荷载进行有限元模拟,分别用不同的材料模型模拟玻璃层和夹层材料,并设置了玻璃的失效应力和应变准则,最后通过试验验证了其模型能够较好的模拟玻璃的失效模式。Zhang等[15]基于LS-DYNA建立了杆状风致飞掷物冲击夹层玻璃的数值模型,并利用该数值模型研究窗户玻璃的易损性与夹层玻璃的尺寸、夹层厚度以及飞掷物的质量、撞击速度等变量的关系。
虽然国内外学者对玻璃抗冲击性能已经进行了大量的研究,但是仍然存在一些不足:① 目前对玻璃抗冲击性能的研究多集中在材料、汽车等学科领域,而风工程对建筑玻璃抵抗风致飞掷物冲击的研究还比较少;② 在研究冲击物对玻璃破坏的影响因素中,大部分研究仅考虑了冲击物的质量和速度两个变量的影响,而忽略了风致飞掷物的形状、冲击姿态和冲击位置等因素的影响;③ 目前研究的玻璃类型多是夹层玻璃,普通民用建筑玻璃(浮法玻璃)的抗冲击性能少有人关注,而在实际的风灾破坏中,这类玻璃是最容易受损的建筑玻璃类型。
本文首先进行了钢球冲击建筑浮法玻璃的破坏试验,并基于LS-DYNA建立了浮法玻璃面板在冲击荷载作用下的有限元模型。然后通过对比试验和数值模拟的结果,验证了飞掷物冲击浮法玻璃有限元模型的准确性。最后,基于验证后的冲击有限元模型,以板状飞掷物为代表,通过数值模拟方法研究风致飞掷物的外形、冲击位置和冲击姿态等特性对建筑浮法玻璃冲击破坏效应的影响。
1 球状飞掷物冲击浮法玻璃的试验和数值模拟
1.1 冲击试验
冲击破坏试验的材料包括冲击物钢球和被冲击物浮法玻璃。钢球采用直径40 mm,质量261 g的实心轴承钢钢球,玻璃采用边长为240 mm×240 mm,厚度分别为3 mm和5 mm的浮法玻璃面板。需要说明的是,玻璃面板四周各预留了20 mm作为边界支撑的空间,所以玻璃面板在试验中的净边长为200 mm×200 mm。
现实中建筑物门窗的玻璃面板通过结构胶与铝合金框架相连接,其边界条件较软弱,故本文试验采用木支架支撑浮法玻璃面板,并通过热熔胶和夹具固定边界,然后将固定好浮法玻璃面板的木支架通过螺丝固定在冲击破坏试验机的工作台台面上,如图1所示。冲击破坏试验机由一个木质工作平台固定一根钢制立杆,杆上连接一根可自由升降的电磁吸盘组成。工作平台平面用于锚固玻璃面板固定支架,并作为冲击跌落的平台。采用电磁吸盘控制钢球下落,按下释放按钮即可使钢球脱离电磁吸盘自由下落。通过升降电磁吸盘的固定杆位置可以自由调节钢球的下落高度,高度调节范围为0~2 700 mm,高度控制的精度为1 mm。

图1 浮法玻璃冲击破坏测试系统Fig.1 Impact failure testing system of the float glass
首先将钢球最初距离玻璃面板的高度调为700 mm,然后释放钢球使其自由下落,冲击点应位于玻璃面板的正中心位置,观察玻璃面板是否被钢球破坏并出现裂纹。如果玻璃面板被破坏了,记录下钢球的下落高度和玻璃面板的裂纹形式。如果玻璃面板没有破坏,将钢球距离玻璃面板的高度提高100 mm再次冲击玻璃面板并观察破坏情况,依此类推,直到玻璃面板被钢球冲击破坏。最后,根据自由落体运动方程(式(1)),由钢球冲击浮法玻璃面板的破坏临界高度计算钢球冲击破坏临界速度。
(1)
1.2 有限元分析模型
本文基于LS-DYNA建立和计算钢球冲击浮法玻璃的有限元模型,并通过HPERVIEW进行可视化后处理。球状飞掷物采用直径40 mm的钢球,网格尺寸为2 mm,浮法玻璃尺寸为200 mm×200 mm×3 mm和200 mm×200 mm×5 mm,网格尺寸为1 mm×1 mm×1 mm,钢球的撞击位置为玻璃板平面的正中心,三维模型如图2所示。

图2 钢球冲击浮法玻璃有限元模型Fig.2 Finite element model of the float glass panel about to be impacted by the steel ball
由于本文仅关注风致飞掷物冲击建筑玻璃的过程,不考虑飞掷物的飞行轨迹,故将钢球与玻璃面板的初始距离设为0.5 mm。然后赋予钢球不同的初始速度,从而确定钢球破坏玻璃面板的临界速度。定义钢球和玻璃板的接触类型为面面接触(surface to surface),接触过程为侵蚀接触(eroding contact)。单元类型采用8节点六面体实体单元Solid164,单元算法采用缺省的常应力单元计算公式。为了避免沙漏能对结果产生影响,通过定义关键字*CONTROL_ HOURGLASS对模型中可能产生的沙漏能进行控制。约束玻璃四边的所有自由度,即边界条件为四边固支。
材料本构模型的选择是有限元模拟中最关键的部分。由于本文主要研究的破坏对象是浮法玻璃,钢球主要提供了冲击荷载的作用,并且钢的刚度远大于玻璃的刚度,因此可以将钢球近似模拟成刚性材料,本构模型为MAT_RIGID,主要材料参数如表1所示。

表1 钢球材料参数(MAT_RIGID)
玻璃是一种典型的脆性材料,其应力应变关系是非线性的,这是由于玻璃内部和表面存在微裂纹和不均匀区,受力时微裂纹将急剧扩展从而引发整个构件破坏,而非均匀性对裂纹扩展方向和贯通模式有重要的影响。因此目前多采用损伤力学方法研究玻璃等脆性材料的微观力学性能,并基于应变等价理论描述玻璃的应力应变关系[16]。JH-2(Johnson Holmquist ceramic constitutive model)模型被认为是最能够体现玻璃和陶瓷等脆性材料力学特征的有限元动态本构模型。Cronin等[17]归纳了以往文献[18-20]中提出的JH-2模型参数,并将JH-2本构模型数值模拟得到的结果与试验结果进行对比,发现二者拟合良好,证明了JH-2本构模型的可靠性。因此,本文选取JH-2本构模型模拟浮法玻璃的材料特性,根据文献建议,本文浮法玻璃的材料参数如表2所示。

表2 浮法玻璃材料参数(JH-2)
1.3 试验和数值模拟结果对比
为了模拟玻璃受冲击作用后出现裂纹或破坏的结果,需要在其有限元模型中定义一个玻璃单元失效准则。本文采用最大主应力,即SIGP1作为玻璃单元的失效准则。需要注意的是,由于钢球强度远大于玻璃,不会在冲击过程中破坏,因此对其不设失效准则。为了确定玻璃合理的最大失效主应力值,本文对SIGP1设定了不同的值进行钢球冲击浮法玻璃的有限元模拟,表3为200 mm×200 mm×3 mm和200 mm×200 mm×5 mm两种尺寸浮法玻璃有限元模型采取不同的SIGP1失效准则得到的破坏结果及其与试验结果的误差。

表3 玻璃不同失效准则对应的钢球破坏临界速度及误差
由表3可知,将玻璃单元最大失效主应力值设为75 MPa,即SIGP1=75 MPa时有限元模拟破坏结果与试验破坏结果最接近,此时3 mm和5 mm两种厚度玻璃面板的误差分别为-6.03%和1.50%,故本文采用SIGP1=75 MPa作为浮法玻璃在冲击荷载下的失效准则。
图3为数值模拟和试验得到的3 mm和5 mm两种厚度玻璃面板被钢球冲击破坏后的裂纹形状和碎片飞溅情况对比。由图3可见,玻璃面板破坏后的裂纹主要有放射状和环状两种形式,其中又以放射状裂纹为主。虽然数值模拟得到的裂纹数量和分布范围小于实际结果,但是也出现了放射状和环状的裂纹形状,能够较准确地反映玻璃面板破坏后的裂纹特征。此外,数值模拟结果还较清晰地体现了玻璃面板受冲击破坏后玻璃碎片飞溅的情况。


(a) 3 mm


(b) 5 mm
综上所述,通过对比试验和有限元数值模拟得到的浮法玻璃在钢球冲击作用下的破坏临界值、裂纹形状及玻璃碎片飞溅情况结果,发现二者的吻合程度都比较好,从而验证了本文所建立的风致飞掷物冲击浮法玻璃有限元模型具有较高的准确性。
2 板状飞掷物冲击效应的数值模拟
Wills等[21]根据风致飞掷物的三维尺寸将其大致分为球状、板状和棍状三种类型,而板状飞掷物是其中最复杂的飞掷物类型。这是因为不同于球状和棍状飞掷物,板状飞掷物外形多变,这不仅会对其飞行特性产生很大的影响,也会对其冲击破坏效应有所影响。基于前文建立且验证后的风致飞掷物冲击浮法玻璃的有限元模型,本章将冲击物由钢球换成钢板,研究板状飞掷物的冲击位置、冲击姿态和外形特性对其冲击效应的影响。
2.1 冲击位置
现实中风致飞掷物冲击建筑玻璃围护结构的落点是随机分布的,不同的冲击落点可能对最终的破坏结果有影响。为了研究浮法玻璃面板在不同位置处抗冲击性能的差异,本节建立了不同落点的板状飞掷物冲击玻璃模型。根据对称性,选择边长为200 mm的正方形浮法玻璃面板上的三个点作为典型的冲击位置,分别代表中心、边部和角部位置,如图4所示。
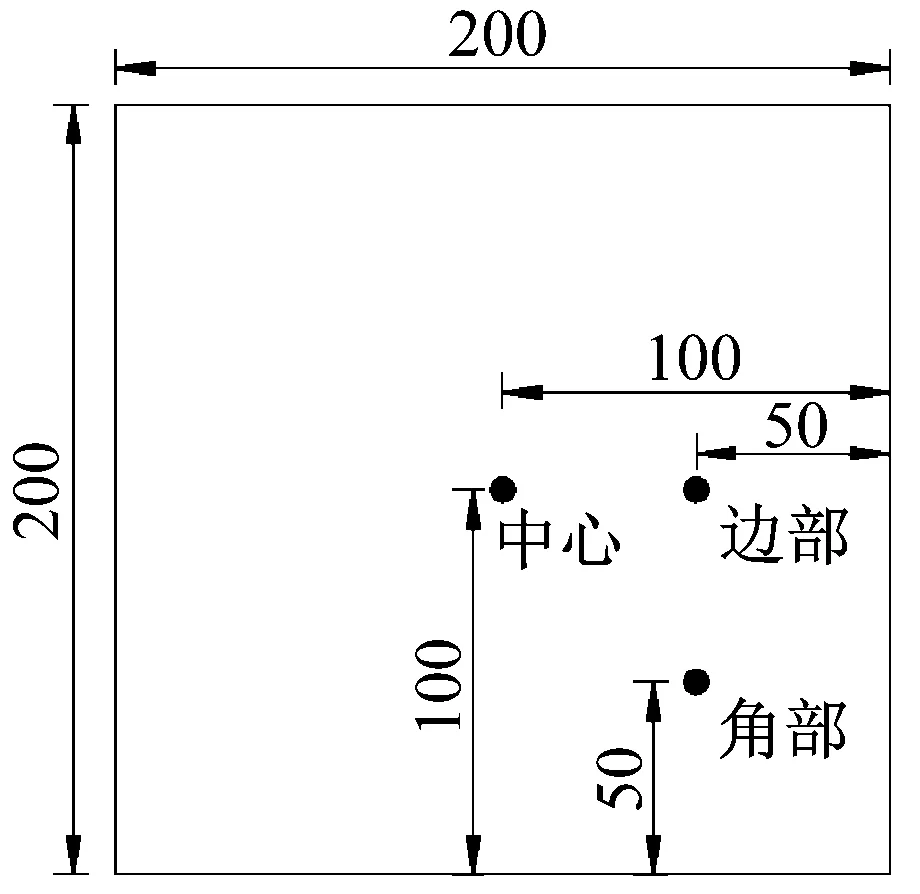
图4 浮法玻璃面板受冲击位置示意图Fig.4 Diagram of the position of float glass panel subjected to the debris impact
在建立板状飞掷物冲击玻璃的数值模型时,除了落点位置不同,板状飞掷物的外形和冲击姿态等其他变量应保持一致。本文采用的板状飞掷物尺寸为40 mm×40 mm×2 mm,冲击姿态为板状飞掷物主面垂直于玻璃面板平面,如图5所示。

图5 板状飞掷物冲击玻璃面板姿态示意图Fig.5 Diagram of the impact attitude of plate-like debris on the float glass panel
图6为冲击位置分别为中心、边部和角部时,玻璃面板被板状飞掷物破坏后的情况。由图6可见,板状飞掷物以主面垂直于玻璃面板平面的姿态冲击玻璃后,玻璃面板的受损区域相对较小,中心和边部破坏的情况近似,角部可能存在一部分玻璃面板脱落破坏的现象。表4统计了板状飞掷物冲击浮法玻璃面板这三个位置的破坏临界速度。由表4可知,钢板分别在中心、边部和角部三个位置冲击浮法玻璃面板的破坏临界速度相差很小。因此,浮法玻璃面板不同位置处的抗冲击性能差异不大,冲击位置对板状飞掷物破坏建筑浮法玻璃结果的影响可以忽略。

(a) 中心

(b) 边部

(c) 角部图6 浮法玻璃面板不同位置受钢板冲击后的破坏情况Fig.6 Failures of the float glass panels subjected to the impact of the steel plate at different positions

表4 钢板冲击浮法玻璃面板不同位置的破坏临界速度
2.2 冲击姿态
在板状飞掷物冲击玻璃的瞬间,既可能是其尖角与玻璃先接触,也可能是棱边或某一个平面与玻璃先接触。因此,板状飞掷物与玻璃面板平面的接触方式存在“点碰撞”、“线碰撞”和“面碰撞”三种类型,这些接触方式由板状飞掷物的冲击姿态所决定,可能是影响其破坏结果的一个重要因素。在三维空间里,板状飞掷物的冲击姿态可以通过X,Y,Z三个坐标轴来确定,本文将板状飞掷物绕X,Y和Z轴旋转的角度分别定义为α、β和γ,如图7所示。
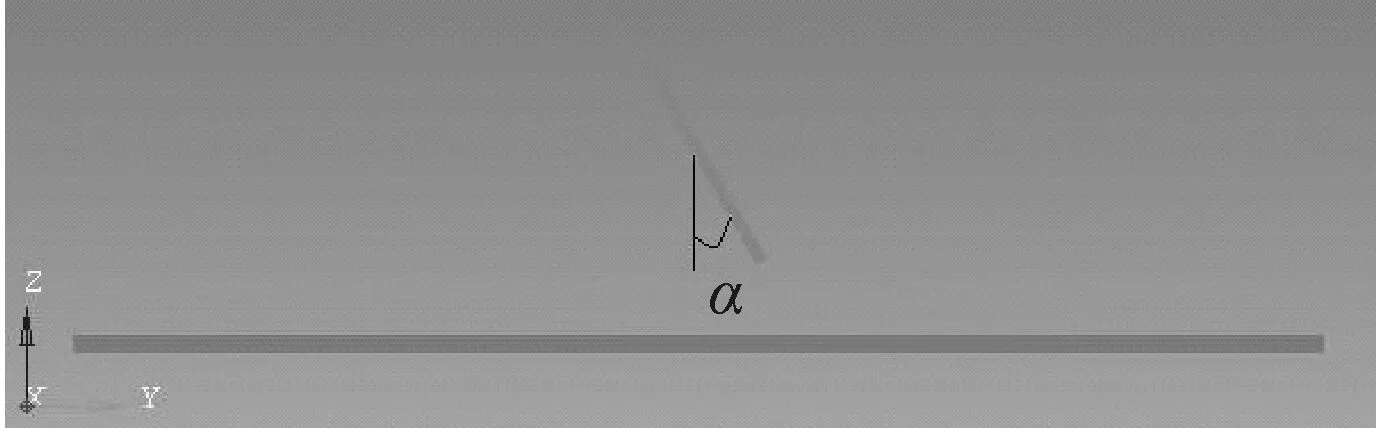
(a) 绕X轴转角α

(b) 绕Y轴转角β

(c) 绕Z轴转角γ图7 板状飞掷物旋转角度定义Fig.7 Definition of the rotation angle of plate-like debris
由前文可知,板状飞掷物的冲击位置对其冲击效应的影响很小,因此根据对称性,可不考虑板状飞掷物绕Z轴旋转时的冲击姿态对最终破坏结果的影响,只需考虑板状飞掷物绕X轴旋转0°~90°,以及绕Y轴旋转0°~45°冲击姿态的影响,即α和β的取值范围分别为0°~90°和0°~45°。本节以15°为间隔对α和β进行取值,由此得到了28种具有代表性的板状飞掷物冲击姿态,并对它们的冲击过程进行了模拟,将破坏结果汇总为表5。同时,表中还备注了各种冲击姿态对应的飞掷物和玻璃面板的接触方式,“P”代表“点碰撞”,“L”代表“线碰撞”,“S”代表“面碰撞”。

表5 不同冲击姿态的钢板冲击玻璃的破坏临界速度
由表5可见,板状飞掷物与浮法玻璃的接触方式,即“点碰撞”、“线碰撞”和“面碰撞”与飞掷物的破坏临界速度之间并没有明显的联系。但是当α=0°时,板状飞掷物的破坏临界速度普遍较小,均小于10 m/s,即更容易破坏建筑浮法玻璃。而当α>0°时,板状飞掷物破坏临界速度普遍较大,均大于10 m/s。为了查明造成这种结果的原因,本文基于数值模拟对全部28种冲击姿态的板状飞掷物在破坏玻璃面板过程中姿态的变化进行了观察与分析。
结果发现,造成α>0°的冲击姿态破坏临界速度普遍较大的原因是板状飞掷物以这些姿态冲击玻璃时,虽然在飞掷物与玻璃面板接触瞬间的接触方式各不相同,但是在随后的冲击过程中板状飞掷物由于受到玻璃面板的阻力将会进一步自由旋转,从而改变了飞掷物与玻璃面板后续的接触方式。最后在破坏和能量转换过程当中,板状飞掷物都将以“面碰撞”的姿态对玻璃面板进行破坏。而在该种冲击姿态下,板状飞掷物与玻璃接触面积较大,能量耗散更快,故较不容易破坏玻璃面板。
限于篇幅,为了对比板状飞掷物以不同姿态冲击后玻璃面板的破坏情况,图8只列出了飞掷物破坏临界速度最小(8.61 m/s,α=0°,β=15°)、中等(9.99 m/s,α=0°,β=0°)以及最大(14.51 m/s,α=45°,β=30°)时,玻璃面板的裂纹开展情况。由图可知,板状飞掷物的破坏临界速度越小,玻璃受破坏的区域也越小。因此,对于板状飞掷物,若其冲击姿态导致其破坏区域越集中,则越容易破坏建筑玻璃围护结构。

(a) α=0°,β=15°

(b) α=0°,β=0°

(c) α=45°,β=30°图8 钢板以不同姿态冲击时,玻璃面板破坏情况对比图Fig.8 Failures of the float glass panels subjected to the impact of the steel plate with different attitudes
2.3 边厚比
板状飞掷物外形较大的差异使其成为风灾中飞行轨迹最复杂的一类风致飞掷物,而其对冲击破坏效应的影响同样不可忽略。由前文可知,板状飞掷物的冲击姿态将会对冲击效应有所影响,而冲击位置的影响可以忽略,因此本节在保证飞掷物冲击姿态相同的情况下,对质量相同,边厚比不同的板状飞掷物冲击效应进行研究。据此,本节共选择了10∶1、15∶1、20∶1、25∶1和30∶1五种边厚比的方形板状飞掷物,对它们冲击浮法玻璃的过程进行了模拟。板状飞掷物的质量均为24.96 g,冲击姿态为α=90°,β=0°,具体尺寸及其破坏临界速度如表6所示。

表6 不同边厚比的钢板尺寸和破坏临界速度
由表6可见,以α=90°,β=0°姿态冲击浮法玻璃时,随着边厚比的增大,板状飞掷物的破坏临界速度也逐渐增大,即边厚比越大的板状飞掷物越不容易破坏玻璃面板。将浮法玻璃面板被这些钢板以该种姿态冲击后的破坏情况列出,如图9所示。由图可见,边厚比越大的飞掷物对玻璃面板的破坏区域越大,破坏临界速度也越大。因此,当板状飞掷物的质量相同时,边厚比越小越容易破坏建筑玻璃围护结构。

(a) 10∶1

(b) 15∶1
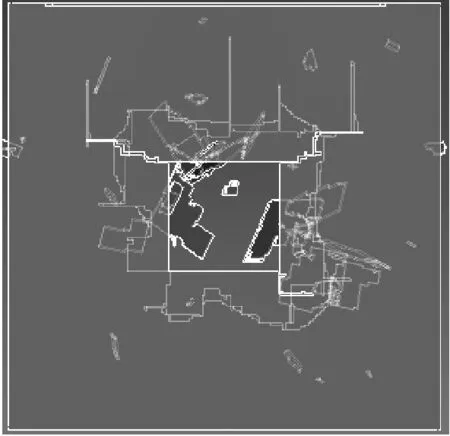
(c) 20∶1
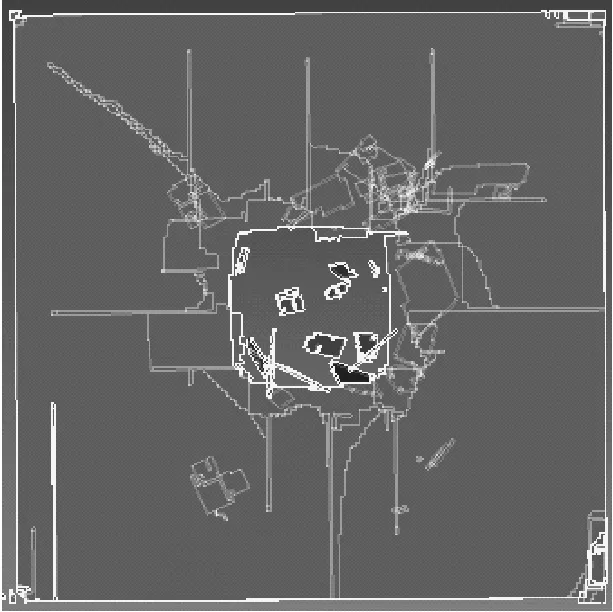
(d) 25∶1

(d) 30∶1图9 不同边厚比的钢板冲击玻璃面板的破坏情况Fig.9 Failures of the float glass panels subjected to the impact of the steel plate with different ratios of side to thickness
3 结 论
本文通过试验和数值模拟研究风致飞掷物对建筑浮法玻璃围护结构的冲击破坏效应。首先采用钢球以不同的速度冲击厚度分别为3 mm和5 mm的浮法玻璃面板进行冲击破坏试验,从而得到钢球的冲击破坏临界速度以及浮法玻璃被破坏后的裂纹和碎片飞溅情况。然后基于有限元动力分析软件LS-DYNA,建立了与试验相对应的飞掷物冲击浮法玻璃面板有限元模型,并通过对比试验和数值模拟的结果,验证了有限元模型的准确性。最后,以板状飞掷物为代表,分析了飞掷物的冲击位置、冲击姿态和外形等特征对其冲击破坏效应的影响。主要结论如下:
(1) 冲击破坏试验结果表明,直径40 mm,质量261 g的钢球破坏3 mm和5 mm厚度浮法玻璃的临界速度分别仅为4.64 m/s和5.34 m/s。因此,建筑浮法玻璃围护结构在风灾中非常容易受到风致飞掷物的冲击而遭受破坏。
(2) 在建筑浮法玻璃的有限元数值模拟中,采用JH-2本构模型作为其材料模型,并以75 MPa最大主应力,即SIGP1=75 MPa作为玻璃的失效判断准则,能够较准确地模拟浮法玻璃在冲击荷载作用下的破坏特性。此外,该有限元模型还能够较准确地模拟浮法玻璃面板被风致飞掷物破坏后的裂纹开展和碎片飞溅情况。因此,本文建立的风致飞掷物冲击浮法玻璃的有限元模型具有较高的可靠性,可用于对风致飞掷物冲击特性的进一步研究。
(3) 板状飞掷物的冲击位置对其冲击破坏效应的影响不大,但是板状飞掷物的冲击姿态和边厚比有较大的影响。板状飞掷物的冲击姿态为主平面垂直于玻璃面板平面(α=0°)时最容易破坏玻璃面板,但是当板状飞掷物以与玻璃面板平面接触面积较大的姿态冲击时,由于破坏区域大、能量耗散快,故较不容易破坏玻璃面板。此时质量相同但边厚比不同的板状飞掷物冲击结果相差也较大,边厚比越小的板状飞掷物越容易破坏玻璃面板。
