新型气磁悬浮轴承的机理研究及仿真分析*
2022-01-27倪喜卓白文鑫竺志大寇海江
倪喜卓,曾 励,白文鑫,张 帆,竺志大,寇海江
(扬州大学机械工程学院,扬州 225127)
0 引言
在高速及精密机械领域,目前常用的轴承有滚动轴承、液体静压轴承、气体静压轴承、主动磁轴承等。其中气体静压轴承与磁悬浮轴承由于具有摩擦阻力小、温度上升幅度小、清洁无污染、无磨损以及能够进行高速传输等优点,成为非接触支承领域的主流技术[1-4]。前者有多种不同的节流形式,节流形式的不同会直接影响其工作性能[5-7],但总体上其动态可调性差。后者又分为主动磁轴承、被动磁轴承和混合磁轴承,其中主动磁轴承可控性良好[8-9]。
将两种轴承结合使用可以扬长避短,形成优势互补,提高轴承承载能力的同时,也可以改善转子系统动力学性能,当某种轴承失效,另一轴承可以补充为保护轴承,实现转子稳定运转。SWANSON等[10]首次发现了将气磁轴承混合使用,提高了系统阻尼、刚度和承载力,但只限于初步试验现象,未给出具体的理论模型。刘暾等[11]以气体轴承为主要承载元件,以电磁轴承修正气体轴承的误差和外界干扰的影响,提高了摆动精度,但未就系统的刚度和悬浮力进行推导和验证。赵宁[12]对气磁轴承中箔片气体动压轴承进行了较为深入的试验,但未能对气磁轴承的综合承载机理和悬浮特性进行研究。PHAM等[13]通过研究发现气磁混合轴承支撑转子系统在临界转速附近的振幅比普通气体轴承降低了26%,但其转子系统结构冗杂。陈素平[14]采用模糊PID控制方法验证了气磁轴承控制系统的可行性和实用性,达到了主轴回转精度的要求,但其仍为组合式传统结构且未对磁轴承部分进行相应的磁场分析。李媛媛[15]将磁气轴承相结合,提高了转子系统的稳定性并改善了系统的动力学特性,但未对气体轴承部分进行流场特性分析。
针对目前气磁混合轴承存在的问题,本文选用一种新型气磁一体化轴承,将静压气体轴承与主动磁轴承相结合组成一个轴承,可以使得转子系统结构简化,具有较小的轴向尺寸。本文介绍了新型气磁悬浮轴承的结构及工作原理。通过有关气压方程以及等效磁路分析,分别建立其压力与磁拉力数学模型,求解出其悬浮力解析表达式,并运用有限元仿真进行分析,验证其承载特性。
1 气磁轴承转子系统的基本组成
在气磁悬浮转子系统中,要使转子实现稳定的悬浮,则需要在5个自由度上施加约束,传统的气磁轴承转子系统结构多为将气体轴承与主动磁轴承混合使用,其结构如图1所示,这种组合方式的转子系统结构较为冗杂。本文所研究的气磁轴承转子系统结构如图2所示,在轴向上使用两个狭缝式气磁轴承代替传统的组合模式,采用这种新型轴承结构,会使得整个轴承转子系统结构简化。

图1 传统气磁轴承转子系统结构
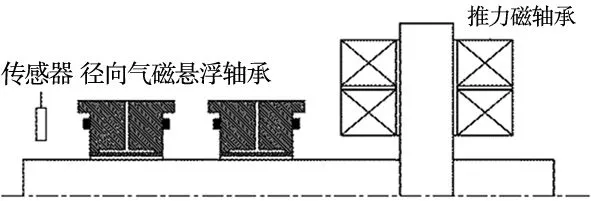
图2 新型气磁悬浮轴承转子系统结构
新型气磁悬浮轴承基本结构及磁路如图3所示。在6个磁极的中心各设置了一个供气孔并通向磁极端部的气腔。狭缝节流器固定在定子的内圈上。气磁悬浮轴承的主要承载力由静压气体轴承部分完成,维持对转子的稳定悬浮。当转子受到扰动时,通过改变主动磁轴承上控制线圈的电流大小,改变轴承的磁拉力将转子恢复平衡状态,实现稳定悬浮。
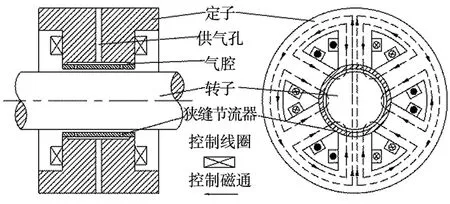
图3 新型气磁悬浮轴承结构及磁路图
2 气磁悬浮轴承的数学模型
2.1 气膜承载力分析
如图4所示为气磁轴承狭缝节流内部结构,在气磁轴承定子上设置了平行排布的双排狭缝。其工作原理与静压气体轴承工作原理一致,由轴承间隙的气膜压力支撑转子保持平衡,其承载力为轴承润滑表面的压力分布。

图4 静压气体轴承结构简图
狭缝式节流静压气体轴承在轴承间隙中的气体流动仍然是雷诺方程:
(1)
式中,h为气膜厚度;P为环境压力;ζ为气体粘度;r为转子半径;ω为角速度。
将雷诺方程无量纲化则有:
(2)
式中,Ps为供气压力;L为轴承长度;ψ为相对间隙,ψ=h0/r。
其边界条件是:
(3)
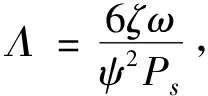




(4)
式中,ε是轴承转子的偏心率。
(5)
轴承承载力Fi为:
(6)
轴承刚度K为:
(7)
2.2 电磁力分析
采用等效磁路法分析该新型气磁轴承,并进行以下假设:忽略系统的磁滞损耗,不发生磁饱和现象,漏磁发生在气隙及供气通道中,磁场沿磁场方向均匀分布,简化后的气磁悬浮轴承等效磁路图如图5所示。

图5 等效磁路图
当转子从轴承中心偏移至坐标(-x,-y)时,得到控制线圈磁导Gn+i(j)的解析式为:
(8)
式中,Gn±i(j)为磁极上控制线圈对应的磁导;u为名义气隙;μ0为相对磁导率;Aa为工作面积。
根据基尔霍夫定律可得:
(9)
式中,φn±为各磁路对应的磁通量;Fmn±为主动控制线圈产生的磁动势。主动磁轴承的磁力计算:
(10)
式中,Ba为磁感应强度;Ha为磁场强度;φ为磁通量。
结合式(8)~式(10),则转子由轴承中心偏移至(-x,-y)坐标时的磁拉力为:
(11)
其中,
(12)
式中,φmn±为各磁路对应的磁通量;G0为定子磁轭磁导;Gp为节流器对应的磁导;GA为转子与气磁轴承定子之间气隙对应的磁导;Fmn±为主动控制线圈产生的磁动势。
综上所述,气磁轴承提供的悬浮力F,其公式为:
F=Fi+Fj
(13)
式中,Fi、Fj分别为是静压轴承部分提供的承载力和电磁轴承提供的磁拉力。
3 气磁悬浮特性仿真分析
3.1 气磁轴承参数
为验证理论分析的正确性,结合磁轴承与狭缝式静压气体轴承结构,轴承定子采用DW310-35硅钢片叠压而成,狭缝节流器采用导磁钢材料,具体结构参数如表1所示。

表1 新型径向气磁悬浮轴承结构参数
3.2 磁场特性分析
为避免出现磁饱和现象,现给定一个饱和磁感应强度BS,当气隙中达到磁饱和强度时,对转子产生最大悬浮力。
在给定电流值为3 A时,得到如图6所示的磁场密度和磁力线云图。从图中可以看出,磁场密度分布与分析结果相同,磁密分布均匀,为磁饱和强度的一半,约为0.65 T。
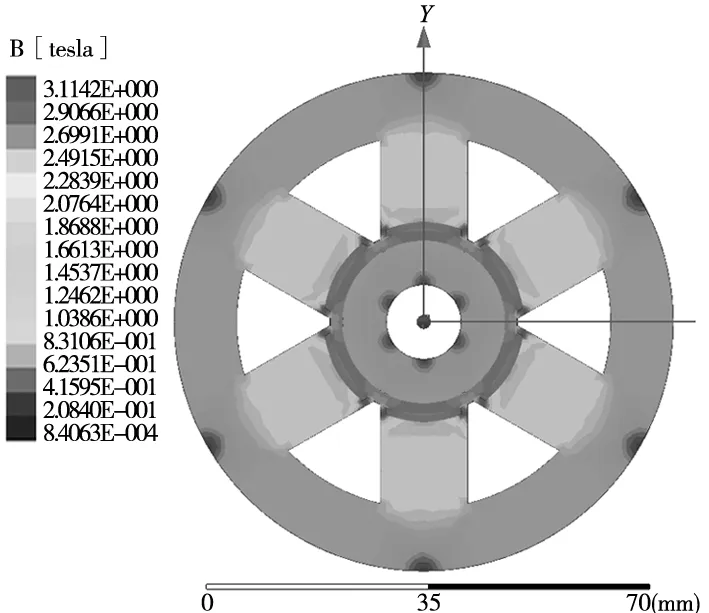
(a)磁场密度分布
如图7所示为供气通道处的磁场密度和磁力线云图。从图中可以看出,磁极处的磁密分布均匀,供气管道结构中受到的磁拉力非常小,可以忽略不计。由图可知,两种模型均满足安培环路定理,并且转子区域发现两者的电流密度有所下降,并从图7a可以看到供气管道的空气区域对磁路产生较大的影响,会伴随着发生磁滞涡流等现象。

(a)磁场密度分布
图8为气隙处的磁感应强度曲线,可以看出,气隙处磁感应强度最高可达到0.63 T,磁轴承工作时,磁路中产生的磁感应强度应为铁磁材料线性段最大值Bmax的1/2,与设定值0.65 T相比,偏差仅为3.07%。

图8 气隙处磁感应强度曲线
当转子位于平衡位置,分别控制x方向与y方向的电流可得到控制电流与悬浮力的关系,如图9所示。可以看出,6极径向主动磁轴承x轴与y轴方向悬浮力与各自方向的控制电流为线性关系。
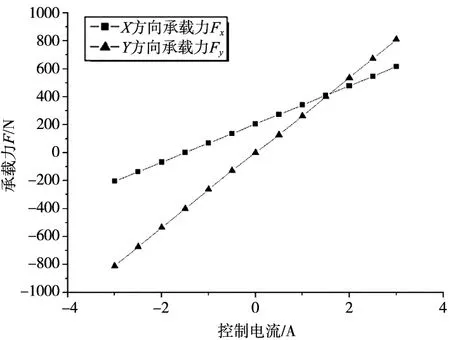
图9 控制电流与承载力关系
3.3 流场特性分析
在0.5 MPa的供气压力下,如图10所示分别为转子偏心率ε=0和ε=0.1时的气模压力分布云图。由图10a可以看出,在整个承载气膜上压力呈对称分布。由图10b可以看到,当偏心率ε=0.1时,气膜厚度大的一侧压力减小,反之,气膜厚度减小的一侧压力增大,两者之间形成压差。仿真结果符合静压气体轴承一般规律。

(a)ε=0
图11为偏心率与承载力,偏心率与轴承刚度的关系。图11a中,气磁轴承的承载力随转子偏心率的增大而增大,在偏心率ε=0.5时,轴承的承载力达到了166 N。图11b中,气体轴承的刚度也是随转子偏心率的增大而增大,但是当转子偏心率ε=0.5时,轴承的刚度提高幅度很小,这是因为当转子偏心过大时,会发生气锤现象导致转子不稳定所致。

(a)偏心率与承载力的关系 (b)偏心率与静态刚度的关系
3.4 气磁耦合特性分析
图12显示了偏心率ε=0.1时,气磁耦合悬浮力对转子作用产生的变形量。转子的变形量表示了气磁悬浮力对转子的作用关系,由图12可以看出,在轴承6个磁极对应的转子位置上产生变形量最大,即6个磁极对应提供的悬浮力最大,符合气磁轴承作用的规律。

图12 转子总变形云图
图13a和图13b分别为单独控制电流和供气压时转子所受到的总变形量。如图13a所示,转子产生的最大变形量大致上呈线性分布。电流I=1 A时,在不同偏心状态下,变化率仅为0.06%。
图13b则可明显看出随着供气压的增大,转子的变形量呈递增趋势。不同偏心状态下转子的最大变形量递增明显。从总体上看,转子所受变形量很小,可忽略不计,且从变化规律可得出该轴承可实现由主动磁轴承承担的线性控制。

(a)最大变形量与电流与偏心率的关系
4 结论
本文提出了一种新型气磁轴承,结合了狭缝式静压气体轴承和主动磁轴承的优势。首先,分析了气磁轴承的结构、工作原理;其次,推导了气磁轴承悬浮力的数学模型;最后,分别对其磁场特性、流场特性以及气磁耦合特性进行了有限元仿真分析,得出如下结论:
(1)新型气磁轴承磁密分布均匀,在供气管道处漏磁较小,可忽略不计,说明该结构合理,可有效避免磁损,减少能耗。电磁拉力与控制电流均呈线性关系,最大拉力可达到819 N。
(2)流场压力分布合理,在轴承主要承载区域可提供稳定的承载力。气膜承载力和刚度随偏心率呈递增趋势,但偏心率过大会导致刚度降低,在设定范围内气磁轴承可以提供较大的承载力和刚度。
(3)新型气磁轴承通过将静压气体轴承和主动磁轴承结合,可以有效减少转子系统轴向长度,结构紧凑。从仿真结果看,以静压气体轴承部分作为主要承载,主动磁轴承部分可提供较宽范围的调节力,轴承的承载范围大,可控性良好。
