长作业杆复杂环境下自寻优避障规划方法研究*
2022-01-27朱瑞明李启光
朱瑞明,李启光,马 飞,李 超
(1.北京信息科技大学机电工程学院,北京 100192;2.北京北开电气股份有限公司,北京 100176)
0 引言
在压铸工艺中有从半封闭熔炉中打捞残渣的工序,目前多是高危环境下的人工作业,亟需采用机械臂取代人工。机械臂控制作业杆末端杷沿着设定的作业轨迹清理,同时避免作业杆与熔炉口碰撞;作业过程中为实现打捞作业要求及防止残渣掉落,需兼顾作业杆姿态限制;此外控制作业杆的机械臂腕关节若与熔炉以及其他周边设备发生干涉,还需要对腕关节轨迹做一定的空间范围限制。在这类半封闭壳体环境下,作业杆作业需满足避开障碍物、姿态可控、机械臂工作空间范围可调三类规划要求。
避障路径规划最常用的是人工势场法[1],因计算效率高且实时性好,广泛运用于避障规划中;由于在很多环境下都无法直接应用,所以大量学者对该方法进行了改进。陈劲峰等[2]引入距离调节因子和屏蔽无效障碍的策略,解决动态避障逃离最优问题;郭彤颖等[3]将蚁群算法和人工势场法结合,实现更佳的逃离局部最优效果;陈满意等[4]提出了低振荡人工势场-ARRT混合算法,实现多障碍环境下的机械臂末端路径规划;WANG等[5]提出了一种基于改进吸引力势函数的人工势场法,实现机械臂避障过程中关节角速度的平滑过渡;刘冰雁等[6]研究了改进人工势场法,实现卫星变轨过程中的避障路径规划;曹博等[7]提出了基于冗余机械臂的人工势场避障算法实现冗余机械臂逃离局部最小的规划;史亚飞等[8]在传统势场中添加速度势场,可以有效逃离局部最小点。根据以上分析,前人研究都是基于机械臂或移动机器人绕开障碍物以及逃离局部最小点这两类问题的改进算法[9-10],并没有涉及到半封闭壳体环境下的长杆避障与姿态控制等运用场景。
针对上述问题,本文提出一个在线自优化的避障算法OSOA。该算法先将半封闭壳体障碍物简化为若干空间杆组成的约束环等效模型,提出约束环势场概念,以解决半封闭壳体避障问题;在此基础上又引入姿态势场以解决作业杆姿态控制问题;引入包络面斥力势场适配驱动端轨迹空间范围约束问题,并将上述三种势场加权叠加形成复合势场。由于作业障碍环境变化不定,按经验适配出的各势场权重值难以规划出最优作业轨迹,本文进一步将复合势场与智能寻优算法结合,实现了在线自优化的避障算法,即OSOA算法。
1 复合势场
1.1 约束环势场
(1)约束环模型
如图1a所示为作业杆出入熔炉壳体通道,标示的两个碰撞边缘是壳体与作业杆易发生碰撞区域,提取出此边缘轮廓,形成如图1b所示的两个空间线段组成的闭环,称该闭环为半封闭壳体的等效约束模型。作业杆穿过约束环内部,不会与壳体碰撞。组成约束闭环的线段称为障碍杆,约束环是空间障碍杆组成的空间闭环。
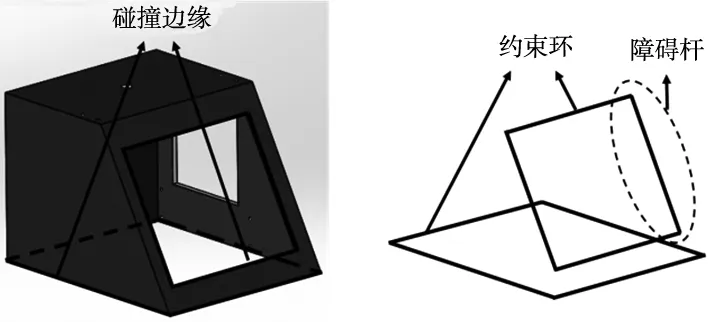
(a)壳体三维图 (b)壳体等效约束环模型
(2)约束环势场的搭建
在约束环势场中,传统人工势场中的两点之间的斥力势场转变成障碍杆和作业杆两条直线之间的斥力势场。该斥力势场将作业杆限制在约束环内部,避免与约束环触碰。如图2所示是处于约束环势场下作业杆作业过程示意图,其中作业端沿着预定作业轨迹运动,作业杆在两个约束环共8个障碍杆的斥力势场约束下,规划出驱动端的驱动轨迹,即避障轨迹。式(1)为约束环势场Urep计算方法,其中,LS为障碍杆和作业杆之间的距离;Vr为势场的单位方向向量,由障碍杆垂直指向作业杆;L0为势场的最大作用范围。
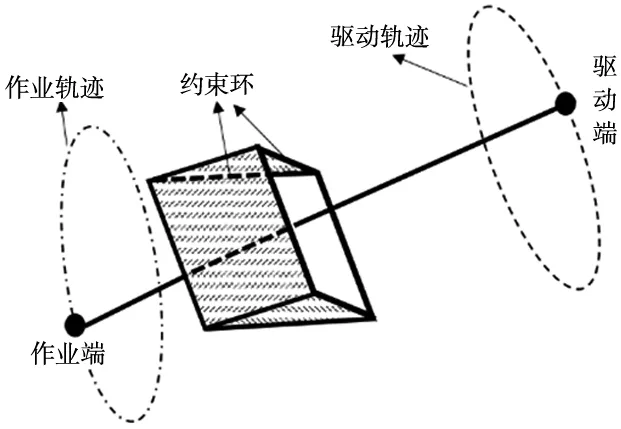
图2 约束环轨迹规划示意图
(1)
1.2 包络面势场
为保障驱动端避障轨迹处于机械臂工作空间内并避开干涉空间,提出了包络面势场概念。本文将包络空间设定为一空间长方体,组成约束空间的各个面即为包络面,如图3所示。驱动端轨迹上的各个节点都会受到指向包络空间内部的驱动力,使整个驱动端轨迹都会约束在包络空间内部。式(2)为包络面势场公式。
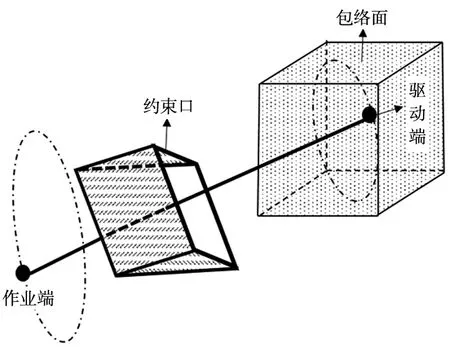
图3 包络面示意图
(2)
式中,Uface为包络面势场;Kf为包络面势场系数;Lf为作业杆驱动端节点到包络面的距离;L1为限幅常数;Vf为包络面势场单位方向向量。
1.3 姿态势场
姿态势场可以在避障的前提下对作业杆的姿态进行小范围的约束控制。
1.3.1 广义坐标
作业杆的作业路径坐标不只空间三维坐标,还包括对应的姿态坐标,即S=[P,θ]。其中,S为广义坐标;P为笛卡尔空间下三维坐标;θ为作业杆的姿态坐标。
1.3.2 角度势场的搭建
作业杆的姿态分为偏航角和俯仰角。因此姿态势场也分为偏航角度势场UYθ和俯仰角度势场UPθ。总的姿态势场Uangle为UYθ和UPθ之和。
(3)
(4)
Uangle=UYθVY+UPθVP
(5)
式(3)中,UYθ为偏航角度势场大小;θYS和θYB分别为某作业节点上作业杆的偏航角设定的最小角度和最大角度,其组成了偏航角度的合适范围;Kθ为角度势场系数;θY为当前作业杆的偏航角度;θ0为限幅常数,俯仰角度势场同理。
式(5)中,Uangle为总的角度势场;VY与VP分别为偏航角度势场和俯仰角度势场的单位方向向量。如图4所示,OA为作业杆;O为作业杆作业端;A为作业杆驱动端;OB为作业杆在XOY平面上的投影。可以求出VY与VP如式(6)、式(7)所示。
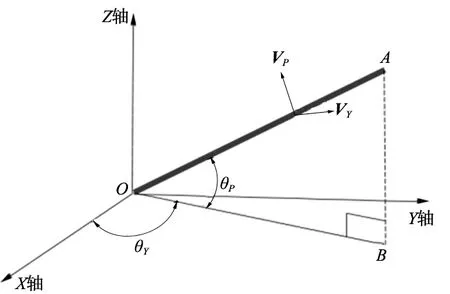
图4 作业杆空间位姿示意图
(6)

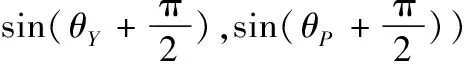
(7)
1.4 复合势场
将约束环势场、姿态势场、包络面势场加权叠加后形成复合势场如下:
Usum=kr∑Urep+kf∑Uface+kaUangle
(8)
式中,Usum为复合势场;kr、kf、ka分别为约束环势场、包络面势场、姿态势场的权重系数。
2 OSOA算法
虽然运用复合势场可以实现在半封闭壳体下的避障路径规划,但很难在不同环境下凭经验权重系数规划出最优的轨迹。因此本文提出了复合势场法和智能寻优算法相结合的OSOA算法,利用寻优算法在线优化复合势场的各权重系数。
2.1 优化参数
因为在障碍环境不变的情况下,复合势场各权重系数是影响规划避障路径的主要因素,设置待优化各权重系数为向量k=[kr,kf,ka]T。
2.2 轨迹寻优评价函数的建立
作业杆驱动端的速度、加速度、角速度、角加速度、工作空间等指标均与驱动机械臂有关。因此这些指标可视为判别轨迹优劣的参考指标。
最大速度与最大角速度会受到机械臂额定性能限值,故提出评价函数如下:
(9)
(10)
式(9)中,f1为轨迹规划过程中最大速度的评价函数;s为避障轨迹路径;ds为轨迹规划过程中的速度值;式(10)中,f2为最大加速度的评价函数;β为作业杆的角度路径;dβ为角速度值。
避障轨迹中加速度和角加速度大小会影响机械臂的稳定及动态响应,因此设计最大加速度和角加速度评价函数如下:
(11)
(12)
式中,f3为加速度评价函数;d2s为轨迹规划的加速度;f4为角加速度评价函数;d2β为角加速度。
为评价包络面势场对轨迹的约束效果,设计评价函数如式(13)所示:
(13)
式中,f5为包络空间约束效果的目标优化函数;pi为轨迹上的点;p∈c为避障轨迹在包络空间内部;ci-pi为点pi到各个包络空间各个面的距离。
此外增加了一个远离约束环的评价函数,如式(14)中f6所示,l为作业杆与约束环最近距离。
f6=1/l
(14)
综合式(9)~式(14),得寻优评价函数如下:
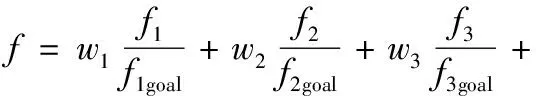

(15)
式中,f为综合评价函数w1~w6为各评价函数的权值且和为1;f1goal~f6goal为估计优化值,作用为使f1~f6各评价函数优化值调整到同一数量级。
2.3 运用粒子群算法优化权重系数
本文以粒子群算法为例对各权重系数k=[kr,kf,ka]T进行优化,粒子群算法的维度设为3,即第i个粒子可以编码成xi={xi1,xi2,xi3},在粒子群算法中,算法的每次迭代都会更新自身位置和速度,公式如下:
(16)
式中,vij(n)和xij(n)分别为粒子i在迭代n次过后,第j维参数的速度和位置;w为粒子的惯性权重;pij为第i个粒子j维参数的极值;gj为全局粒子j维参数的极值;c1为自生的学习因子;c2为社会学习因子;r1与r2为(0,1)之间的随机数。
2.4 OSOA算法流程
OSOA算法流程图如图5所示,具体算法流程如下:

图5 OSOA算法流程图
步骤1: 确定算法参数,如种群规模,迭代次数,权值范围,优化区间,初始化粒子群等;
步骤2: 将粒子参数作为复合势场系数带入复合势场中,并进行轨迹规划,得出规划轨迹的动力学参数。
步骤3: 将步骤2中的动力学参数带入评价函数式(15)中,计算各个粒子的适应度。
步骤4: 由步骤3求得的粒子适应度带入式(17)中更新粒子的位置、速度以及粒子群的极值。
步骤5: 判断算法是否超出最大迭代次数或粒子是否收敛于设定区间,若否,转至步骤2继续迭代,若是,输出最优粒子。
步骤6:将最优粒子参数作为复合势场系数,规划出最优轨迹。
3 仿真及结果分析
3.1 复合势场姿态控制仿真
为验证复合势场中的姿态势场对作业杆姿态规划能力,构建仿真试验环境如图6所示,其中约束环由一个四边型框和一个空间立体的六边形组成。作业轨迹为点画线S,起点S1、终点S2。假设工序要求作业杆在S1姿态为(10,80)度,S2姿态为(0,80)度。姿态第一个数值为作业杆偏航角,第二个数值为俯仰角。

图6 姿态控制三维图
具体试验步骤如下:在作业杆作业端沿着轨迹S从S1运动到S2时,无姿态势场下规划的驱动端位姿从L1运动到L2;姿态势场下的驱动端位姿会从L1θ运动到L2θ。
仿真规划出的驱动端试验数据如表1所示。可以看出姿态势场下L1θ、L2θ角度贴近工序要求的角度,而未经姿态势场规划的L1、L2角度不满足要求。
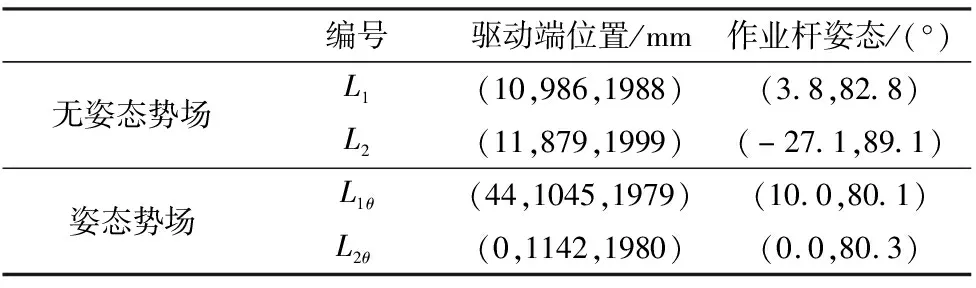
表1 作业轨迹坐标集
作业杆角度规划如图7所示。从该试验看出无姿态势场规划的避障轨迹中作业杆姿态不可控,加上姿态势场可以有效地控制作业杆在作业时的姿态。

图7 作业杆姿态图
3.2 OSOA路径寻优仿真
为验证OSOA算法的寻优能力,搭建试验环境为实际熔炉的等效约束环,作业轨迹为一椭圆,四周无干涉物,作业任务对杆姿态无要求,作业时间为20 s。
试验参数:粒子群规模为30,最大迭代次数30次,c1=1,c2=1,w=1。由于杆姿态无要求,故优化参数无姿态势场系数,优化参数为(kr,kf),参数优化空间皆为[1,100],粒子维度为2。评价函数参数为:w1=0.1,w2=0,w3=0.1,w4=0,w5=0.4,w6=0.4,f1goal=0.1,f2goal=0.05,f3goal=0.1,f4goal=0.05,f5goal=0.2,f6goal=0.01。
试验结果分析:初始规划如图8所示,粒子群初始在优化空间随机分布,初始轨迹由复合势场规划得出,可以看出虽然避障轨迹在包络空间内,但所占空间范围较大。经过5次迭代优化后,粒子群分布图以及轨迹优化图如图9所示,粒子逐渐往评价函数最小处靠拢,避障轨迹逐渐缩小。迭代30次完成后,形成如图10所示的最终优化图,粒子收敛于kr=5.1,kf=100处,此时规划出最优轨迹。
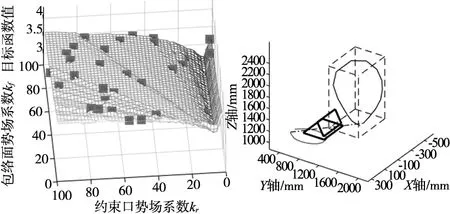
(a)初始化粒子分布图 (b)初始轨迹

(a)迭代5次粒子分布图 (b)迭代5次优化轨迹

(a)迭代完成粒子分布图 (b)最终优化轨迹
初始轨迹和最优轨迹的运动学性能对比如图11~图13所示,由图11可以明确看出最优轨迹所占空间比初始轨迹小,对机械臂的灵活工作空间范围需求更小;由图12可以看出最优轨迹的速度比初始轨迹的速度更平缓,对电机的负载要求更小;由图13可以看出最优轨迹加速度整体趋近于零,表明最优轨迹对机械臂的负载明显小于初始轨迹。最终的优化幅度如表2所示。

图11 规划轨迹位置曲线图
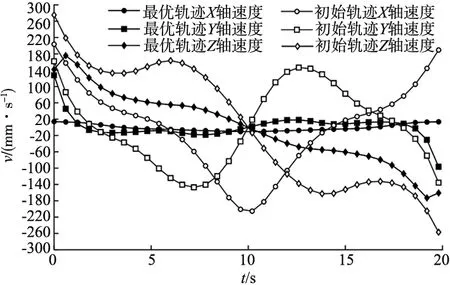
图12 规划轨迹速度曲线图

图13 规划轨迹加速度曲线图

表2 OSOA较复合势场性能提升表
4 结束语
提出复合势场方法,解决了半封闭壳体多约束环境下长作业杆避障规划问题,且复合势场不限于文中提出的几种拓展势场,可以根据约束环境进一步拓展新的势场。在此基础上提出OSOA算法,实现在不同作业障碍环境下自寻优获取最优路径。OSOA算法将作业杆驱动端位置、速度、加速度等不同量纲的约束条件融于评价函数中,为后续进一步依据作业杆驱动系统自身特性指标优化最优路径提供可行的途径。
本文算例中OSOA算法仿真时间约为128 s左右,只适用于静态障碍环境的避障规划,对于动态环境下的实时避障规划需要进一步提高寻优效率。
