滚珠丝杠副轴向静刚度确信可靠性建模与分析*
2022-01-27龚梦辉周长光冯虎田
龚梦辉,韩 军,周长光,冯虎田,欧 屹
(南京理工大学机械工程学院,南京 210094)
0 引言
滚珠丝杠副是一种能将直线运动与旋转运动相互转化的关键传动功能件,因其传动效率高、驱动速度快、定位精度高等特点,被广泛应用于数控机床、航空航天、农业生产等领域。滚珠丝杠副的刚性是衡量其综合性能的重要的指标之一,不仅影响滚珠丝杠副的精度、承载能力和使用寿命,还影响装备的工作效率和使用寿命。因此,对滚珠丝杠副的刚度进行可靠性分析及优化,对于提高装备的可靠性具有重要意义。
目前很多学者在滚珠丝杠副刚性的理论建模方面做了大量研究。例如黄金宝建立双螺母垫片预紧滚珠丝杠副的刚度模型时考虑了滚珠丝杠副在受轴向载荷时接触角的变化对其影响[1];刘涛[2]在建立自适应预紧滚珠丝杠副刚度模型时,分析了预紧力与变形之间的关系;张义民等[3]建立了单螺母滚珠丝杠副轴向静刚度模型;DIEGO等[4]基于接触应力建立了一种新型的滚珠丝杠副接触变形与优化模型;DADALAU等[5]提出了一种有效的计算滚珠丝杠副刚度的方法。
以上研究对滚珠丝杠副的刚度可靠性计算奠定了良好的理论基础。例如魏宗平[6]采用区间理论的方法计算了轴向接触静刚度的可靠度;张义民等[3]采用改进的一次二阶矩法对单螺母滚珠丝杠副的轴向静刚度的可靠性进行了研究,该方法对参数的信息量要求较高;王丹等[7]采用蒙特卡洛仿真法对滚珠丝杠副的轴向静刚度进行了分析,但是需要较大的样本量;黄宽等[8]提出的基于Halton序列拟蒙特卡洛方法虽然克服了这些缺点,但是仅考虑了参数的不确定性。
在研究滚珠丝杠副的刚度可靠性时,除了需要考虑参数固有不确定性外,还需考虑因技术人员的知识不完备而造成的认知不确定性[9]。确信可靠度理论的提出为可靠性分析打开了新的思路,该理论能对随机不确定性和认知不确定性进行量化。LIU[10]首次提出了确信可靠度的概念,并建立了确信可靠度度量体系。ZENG等[11]提出了设计裕量、随机不确定性因子和认知不确定性因子的确定方法。
本文基于确信可靠性理论,考虑固有不确定性和认知不确定性,对双螺母垫片预紧式滚珠丝杠副的轴向静刚度进行可靠性分析,并与现阶段常用的蒙特卡洛仿真法计算的可靠度进行对比。并基于确信可靠性模型,对随机不确定性因子和认知不确定性因子进行灵敏度分析,以提出行之有效的滚珠丝杠副可靠性增长策略。
1 确信可靠度分析方法
确信可靠度理论是以不确定度理论[12]、概率论和机会理论[13]三大数学理论为基础的可靠性理论,可用不确定度理论描述认知不确定度,用概率论描述随机不确定度,用机会理论描述随机不确定度和认知不确定度同时存在的混合不确定度。确信可靠性的度量框架图,如图1所示。

图1 确信可靠性度量框图
在确信可靠性理论中性能裕量m是描述系统功能行为的状态变量,表征的是性能参数p与其故障阈值pth之间的距离或相对距离。根据性能参数p和故障阈值pth的关系,性能参数的类型有3种:
(1)望小性能参数(STB):当p≥pth时,产品发生故障,则性能参数为望小性能参数;
(2)望大性能参数(LTB):当p≤pth时,产品发生故障,则性能参数为望大性能参数;
(3)望目性能参数(NTB):当p≤pth,L或p≥pth,U时,产品发生故障,则性能参数为望目性能参数;
不同类型的性能参数,其对应的性能裕量也不同:
(1)
基于康锐等建立的系统确信可靠度评估计算方法[11],本文将同时考虑滚珠丝杠副的参数和模型不确定性对性能裕量模型的影响,在建立滚珠丝杠副刚度模型的基础上,从设计裕量、随机不确定性因子(aleatory uncertainty factor,AUF)和认知不确定性因子(epistemic uncertainty factor,EUF)的角度出发,建立基于性能裕量的滚珠丝杠副确信可靠性模型,计算滚珠丝杠副轴向静刚度的可靠性指标。
2 滚珠丝杠副轴向静刚度建模
滚珠丝杠副的刚度是指其抵抗变形的能力,表示为单位载荷下的变形量,因此本文以滚珠丝杠副的轴向变形量来对刚度进行量化。对于双螺母垫片预紧式滚珠丝杠螺母,在空载情况下,左右两边螺母只受初始预紧力Fp作用,受力如图2所示。图3为以滚珠中心为原点建立的坐标系,图中α为滚珠与滚道之间的接触角,β为螺旋升角,滚珠与左右螺母滚道接触面的法向载荷为:

图2 空载下垫片预紧式双螺母滚珠丝杠副示意图
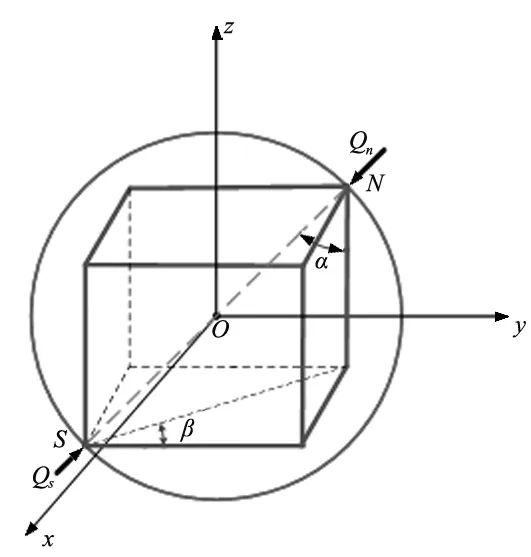
图3 滚珠坐标系
(2)
式中,i为单个螺母滚珠循环圈数;z为单圈承载滚珠数。
对单个滚珠而言,其法向变形量为滚珠与螺母滚道、丝杠滚道法向变形量之和。根据赫兹定理,在初始预紧力作用下,滚珠丝杠副的法向变形量为:


(3)
式中,∑ρs、∑ρn分别为丝杠和螺母与滚道接触点处的主曲率和;μ1、μ2为泊松比;E1、E2为弹性模量;E′为当量弹性模量;ma为接触椭圆长轴系数;e为椭圆偏心率;K(e)为第一类完全椭圆积分。
在弹性范围内,滚珠丝杠副轴向变形量与法向变形量的关系[14]为:
(4)
滚珠丝杠副轴向变形量为:


(5)
当滚珠丝杠副承受轴向载荷Fa时,其受力如图4所示,此时螺母2为工作螺母,所受力由Fp增加为F2,螺母1为预紧螺母,所受力由Fp减小为F1。

图4 受轴向载荷垫片预紧式双螺母滚珠丝杠副示意图
根据受力平衡条件:
F2-F1=Fa
(6)
根据变形协调关系[6]:
(7)
对于式(7)的非线性方程,可用Newton-Raphson迭代法[6]求解。
由静力平衡方程,螺母1中滚珠承受的法向力为:
(8)
螺母2中滚珠承受的法向力为:
(9)
螺母1和2相对于丝杠的轴向变形量为:
(10)
由于螺母1、2及滚珠的材料参数相同,且滚珠丝杠本身存在预紧力,因此两螺母轴向刚度一致,即螺母1和2轴向变形量变化相同:
Δ1=Δ2=δp-δ1=δ2-δp
(11)
因此,在轴向载荷Fa作用下,双螺母垫片预紧式滚珠丝杠副轴向变形量为:


(12)
从式(12)看出,双螺母垫片预紧式滚珠丝杠副的轴向变形量与结构参数、材料参数、预紧力和轴向载荷有关。
3 滚珠丝杠副确信可靠性建模
滚珠丝杠副在加工制造过程中,由于存在误差,其相关结构参数与理论值存在一定的偏差,如节圆直径D、压力角α、适应比f、滚珠直径d、螺旋升角β等。现阶段,对于滚珠丝杠副的可靠性计算,都是基于经验假设,其分布模型和分布参数都是依据经验所得,缺乏理论依据,因此,必须考虑参数不确定性和模型不确定性对滚珠丝杠副可靠度的影响。
根据定义可知,滚珠丝杠副的轴向变形量为望小性能参数,其故障阈值为pth=Δ,性能参数为p:
p=Δa(D,α,β,f,d,Fa,Fp)
(13)
则性能裕量为:
(14)
为计算考虑参数和模型不确定性的确信可靠度,首先得明确设计裕量、随机不确定性因子和认知不确定性因子。
3.1 设计裕量
滚珠丝杠副的设计裕量md定义为:
md=gm(xN)
(15)
式中,xN为D、α、β、f、d、Fa、Fp的均值组成的向量。
3.2 滚珠丝杠副随机不确定性因子的确定方法
随机不确定性因子描述了滚珠丝杠副参数随机变化的分散性,例如制造误差、材料特性变化等。根据定义[11],随机不确定性因子为:
(16)
式中,ZRp为标准概率正态分布的累积函数在Rp处的取值:
(17)
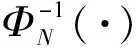
理论上可靠度Rp可通过概率密度求得,但由于滚珠丝杠副刚性的影响因素较多,求解联合密度式较困难。目前,求解经典概率可靠度较常用的方法是蒙特卡洛仿真法[15]和结构可靠性方法[16],本文将采用蒙特卡洛仿真法求解Rp。
3.3 滚珠丝杠副认知不确定性因子的评估方法
认知不确定性描述性能裕量分布的分散性,其分散程度的大小取决于产品故障过程及规律的认知程度。一般来说对产品故障的认知越充分,认知不确定性因子的值越小。在工程上,技术成熟度等级系统[17]描述了典型产品制造和加工过程,描述了技术从基本概念发展到成功实践的全过程,反映了人们对相关技术的认知从无到逐渐完善的过程,已被广泛应用于航空航天等多个领域[18]。技术成熟度等级(technology readiness level,TRL)能够很好地刻画人们的认知不确定度水平,因此可以基于技术成熟度等级来对滚珠丝杠副的认知不确定性因子进行量化。
(1)基于条件距离的专家权重的计算
邀请n位专家对滚珠丝杠副的技术成熟度等级条件质量进行打分,需打分的条件有m个,则第i个条件的分数记为:Qi,1,Qi,2,…,Qi,n。第i个条件的平均条件质量为:
(18)
条件距离为:
(19)
基于条件距离的专家权重为:
(20)
(2)基于贡献的条件权重计算
第i个条件的条件质量为:
(21)
条件权重为:
(22)
(3)计算等级得分
技术等级得分表示滚珠丝杠副在某一技术成熟度等级下的表现,假设滚珠丝杠副当前技术成熟度等级为N,则其等级得分为:
(23)
(4)计算技术成熟度得分
技术成熟度得分表征的是在技术发展周期内,滚珠丝杠副的成熟程度。假设滚珠丝杠副技术成熟度共有Nmax级,则技术成熟度得分为:
(24)
(5)计算认知不确定性因子
求得技术成熟度得分后,滚珠丝杠副的认知不确定性因子为:
(25)
图5为认知不确定性与技术成熟度得分的关系图。从图中可以看出,不同技术成熟度等级下,技术成熟度得分不同,呈现分段特性。技术成熟度等级越高,技术成熟度得分越大,认知不确定性因子也就越低,且在同一技术成熟度等级下,当技术成熟度得分较小时,其对认知不确定性因子的影响较大,随着技术成熟度得分的增大,这种影响会显著减小,说明在同一个技术成熟度等级下,单靠提升技术成熟度得分只能在一定程度上提升产品的可靠性。

图5 认知不确定性因子与技术成熟度得分关系图
3.4 滚珠丝杠副确信可靠度计算
将设计裕量md、随机不确定性因子σm、认知不确定性因子σe代入式(26),即可算出滚珠丝杠副确信不确定度。
(26)
式中,Φ(·)为标准正态累积分布函数。
4 滚珠丝杠副确信可靠性实例分析
本次计算采用丝杠型号为FC1Z-4010-3,相关参数如表1所示。假设滚珠丝杠副的节圆直径D、接触角α、螺旋升角β、滚珠适应比f、滚珠直径d、轴向载荷Fa、初始预紧力Fp等参数服从正态分布,取均值的5%作为其标准差。

表1 滚珠丝杠副参数表
采用蒙特卡洛仿真法,取100 000次抽样得到概率可靠度Rp=0.920 41,其分布图如图6所示。从图中可以看出,滚珠丝杠副的轴向变形量的分布呈近似正态分布。
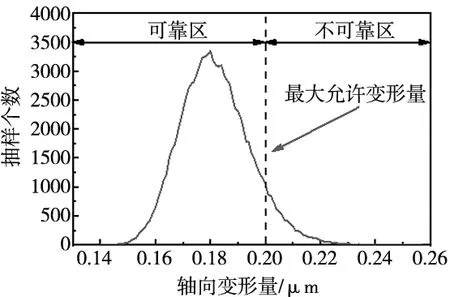
图6 蒙特卡洛法分布图
查标准正态分布表得ZRp=1.407。计算得设计裕量为md=0.197 4,随机不确定性因子为:σm=0.140 3。
根据GJB7688[17]可知,成熟滚珠丝杠副产品的技术成熟度等级为9级,设计阶段滚珠丝杠副产品的技术成熟度等级则在1~8级。根据不同的等级条件,通过专家打分,计算得9种技术成熟度等级下的等级得分、技术成熟度得分、认知不确定性因子如表 2所示。
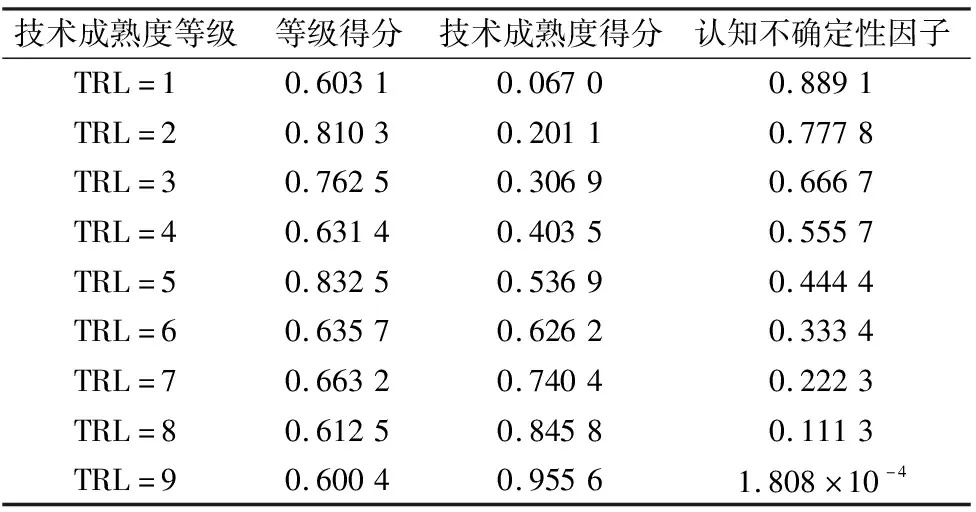
表2 不同技术成熟度等级条件下认知不确定性数值
基于蒙特卡洛法计算的可靠度及基于不同技术度成熟度等级下的确信可靠性方法计算的可靠度如表3所示,从表3中,我们可以得出:确信可靠性理论计算的结果比蒙特卡洛法更加保守,说明在考虑认知不确定后,滚珠丝杠副的轴向静刚度可靠性会降低,也说明由于认知不足产生的认知不确定性对滚珠丝杠副的可靠性提升具有阻碍作用,随着技术成熟度等级的提高,人们对于滚珠丝杠副的认知更充分,认知不确定性因子会降低,滚珠丝杠副的确信可靠度会显著提高,可见通过系统学习,弥补对丝杠认知上的缺陷对于滚珠丝杠副可靠性提升是十分必要的。
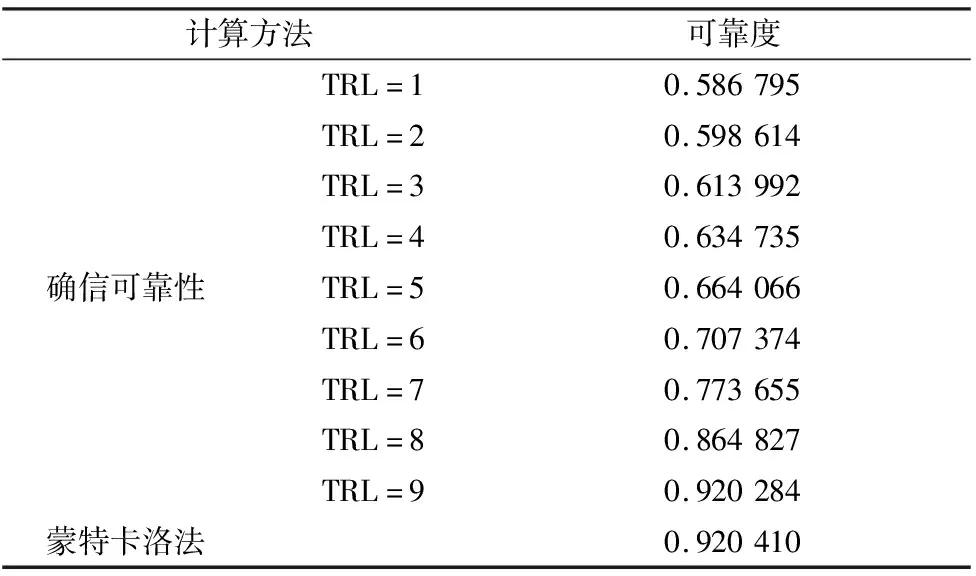
表3 可靠度计算值
5 滚珠丝杠副确信可靠性灵敏度分析
为研究随机不确定性因子和认知不确定对因子对滚珠丝杠副确信可靠度的影响,本节对其进行灵敏度分析。首先确定这两个参数的取值范围。计算设计裕量md为0.197 4;取滚珠丝杠副概率可靠度Rp为范围为[0.7,1],对应随机不确定性因子σm范围为[0,0.379 6];通过仿真可得,式(23)中的等级得分LN的取值范围为[0,1],取技术成熟度为5~9级,认知不确定性因子范围为(0,0.555 6)。
图7为不同认知不确定性因子下滚珠丝杠副的确信可靠度随着随机不确定性因子变化情况;图8为不同技术成熟度等级下所能达到的最大确信可靠度曲线图;图9为技术成熟度等级从5级到9级时滚珠丝杠副确信可靠度随认知不确定性因子σe和随机不确定性因子σm变化图,其中图9a为三维图,图9b为等值线图,图中虚线表示滚珠丝杠副的轴向静刚度确信可靠度RB为0.9的等值线。

图7 确信可靠度随σm和σe变化曲线图

图8 各技术成熟度等级最大确信可靠性
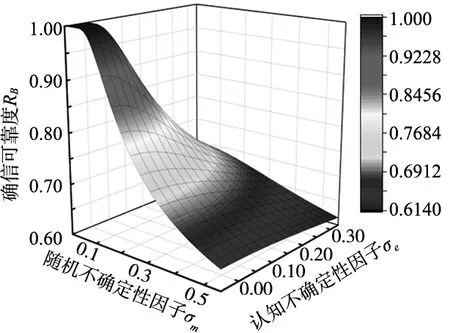
(a)三维图
通过图7可以看出,当随机不确定性因子较大时,认知不确定性因子对滚珠丝杠副的确信可靠度影响较小。当随机不确定性因子减小时,认知不确定性因子对滚珠丝杠副确信可靠度影响程度增大。因此,在对滚珠丝杠副刚性进行可靠性提升时,在初期,应通过优化滚珠丝杠副的结构参数来减小随机不确定性因子,提高滚珠丝杠副的确信可靠度。当随机不确定性因子减小到一定值后,若通过优化滚珠丝杠副的结构参数来提高可靠度,成本将会激增,提升效果也不明显,因此,后期应加强对员工的培训,完善其知识体系,减小认知不确定性的影响,达到确信可靠度增长的目的。
通过图8可以看出当技术成熟度等级小于8级时,最大可靠度均小于0.9,这是因为当技术成熟度较低时我们对滚珠丝杠副的了解还不够深入,从而制约了滚珠丝杠副的可靠性增长,因此,减小认知不确定性的影响是保证滚珠丝杠副可靠性增长的必经之路。
从图9中可以看出,随着随机不确定性因子和认知不确定性因子的减小,滚珠丝杠副的确信可靠度能够得到显著提升。且由于认知不确定性的存在,滚珠丝杠副的确信可靠度总是比概率可靠度小,只有当认知不确定性因子趋近于0时,确信可靠度才趋于概率可靠度;当随机不确定性因子和认知不确定性因子都趋于0时,若md>0,则确信可靠度趋向于1,此时确信可靠度几乎不受不确定性的影响,只由设计裕量决定,即初始设计是可靠的(md>0),则滚珠丝杠副就是可靠的。一般情况下,滚珠丝杠副的可靠性应保证在0.9以上,从图9b中可以看出,必须使认知不确定性因子σe小于0.15,才能保证滚珠丝杠副的可靠度满足规定要求。
6 结束语
本文在滚珠丝杠副刚度模型中,考虑了参数和模型不确定导致的认知不确定性对性能裕量的影响,从设计裕量、随机不确定性因子、认知不确定性因子出发,建立了基于性能裕量的确信可靠性模型,求得在不同技术成熟度等级下双螺母垫片预紧式滚珠丝杠副的轴向静刚度确信可靠度并对其进行了灵敏度分析,通过分析得出:
(1)考虑了认知不确定性后,滚珠丝杠副的轴向静刚度可靠度明显降低,只有当认知不确定性因子趋于0时,确信可靠度才趋于概率可靠度,当随机不确定性因子和认知不确定性因子都趋于0时,若md>0,则确信可靠度趋向于1。提高技术成熟度等级能够减小认知不确定性的影响,提升可靠性,随着技术成熟度等级从1级提升到9级,确信可靠度从0.586 795显著提升到0.920 284,且达到9级时,可靠度与采用蒙特卡洛法所求的0.920 410接近。
(2)当滚珠丝杠副可靠性较小时,随机不确定性因子对其确信可靠性影响较大,当其可靠性提升到一定程度后,认知不确定性因子对确信可靠度影响更大。
(3)当滚珠丝杠副可靠性较低时应通过优化丝杠结构参数来获得可靠性增长,当可靠性增长到一定值时,应加强对技术人员培训,以减小认知不确定性的影响,获得可靠性增长,且为了保证滚珠丝杠副可靠度达到0.9以上,必须确保认知不确定因子小于0.15。
