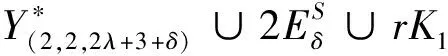形树的伴随多项式的分解及其补图的色等价性

熊鹏飞，张秉儒

(1.青海交通职业技术学院，青海 西宁 810006；2.青海师范大学数学与统计学院,青海 西宁 810008)

1 预备知识

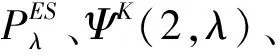
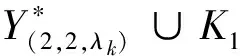
2 图的伴随多项式的概念

设G是p的阶图,若图G的生成子图G0的所有分支是完全图，则称G0为G图的理想子图。用bi(G)表示图G的具有p-i个分支的理想子图的个数(0≤i≤p-1),由文[4]的定理15可知

(1)

这里是p=|V(G)|,(λ)k=λ(λ-1)(λ-2)…(λ-k+1)。

定义2.1[5]设G是p阶图，则图G的多项式

(2)

称为简单图G的伴随多项式，h(G，x)可以简记为h(G)。

图G的每个分支或是K1或是K2的生成子图称为图G的一个匹配，图G的一个k-匹配就是含有k条边的匹配，由G的理想子图的个数bi(G)的定义即得如下的

引理2.1[5]若G是无三角形K3的图，则bi(G)等于图G的i-匹配的数目。

定义2.2称图G与H是伴随等价的，若h(G，x)=h(H,x)；称图G是伴随唯一的，若从h(H,x)=h(G，x)推出图G与H同构，记为H≌G。

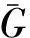
我们常用到图的伴随多项式h(G，x)的如下的基本性质：

引理2.3[7]设uv∈E(G)且uv不属于图G的任何三角形，则有

h(G，x)=h(G-uv,x)+xh(G-{u,v},x)

引理2.4[7]设图G具有k个分支G1,G2,…,Gk，则有

h(G，x)=h(G1x)h(G2,x)…h(Gk,x)=

设G是任意的连通图，其伴随多项式h(G，x)以下简记为h(G)。并不再赘述。

根据引理2.4,我们容易推知如下的

引理2.5设G和H是任意的两个图，K1是一个孤立点，n≥2是任意的自然数，则有

(ⅰ)h(H∪nG)=h(H)h(nG)=

h(H)hn(G)；

(ⅱ)h(H∪nK1)=h(H)h(nK1)=

xnh(H)

引理2.6[9-10]设n≥2是自然数，Pn表示具有n个顶点的路，则有

(ⅰ)h(Pm+1)=xh(Pm)+xh(Pm-1)

(3)

(ⅱ)h(Pm+n)=h(Pm)h(Pn)+

xh(Pm-1)h(Pn-1)

(4)

引理2.7[11]设∀k∈N,m(≥3)是自然数，Ψ(k,m)表示把星图Sk+1的唯一k度点与Pm的一个1度点重迭后得到的图,则有

(ⅰ)h(Ψ(2,m))=x2[h(Pm)+2h(Pm-1)]

(5)

(ⅱ)h(Ψ(k,m))=xk[h(Pm)+kh(Pm-1)]

(6)

3 几类新图的伴随多项式

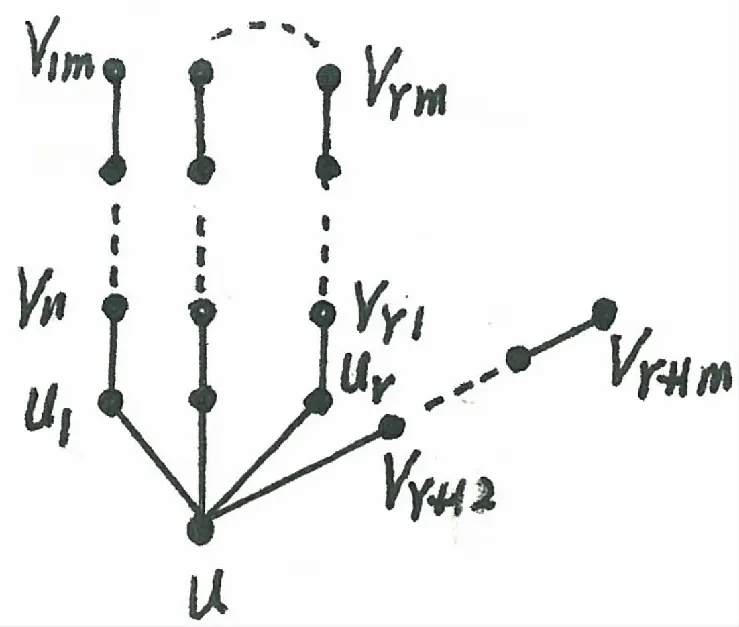
图1 图

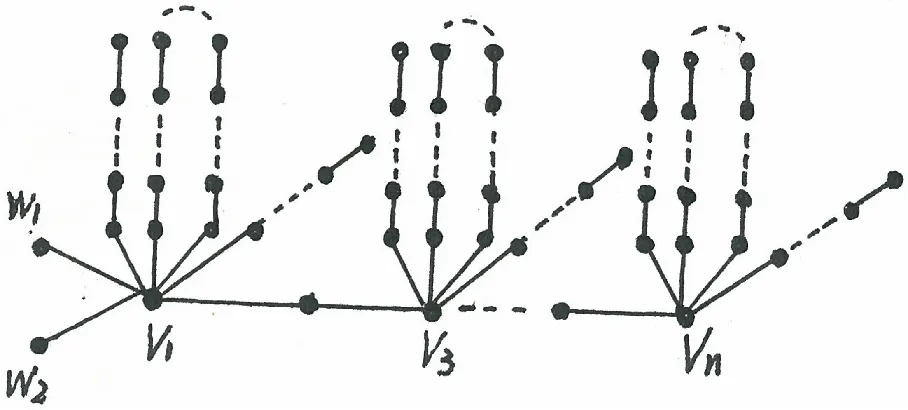
图2 图ΨK(2,λ)，λ=n+2-1(n+1)δ

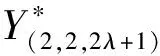
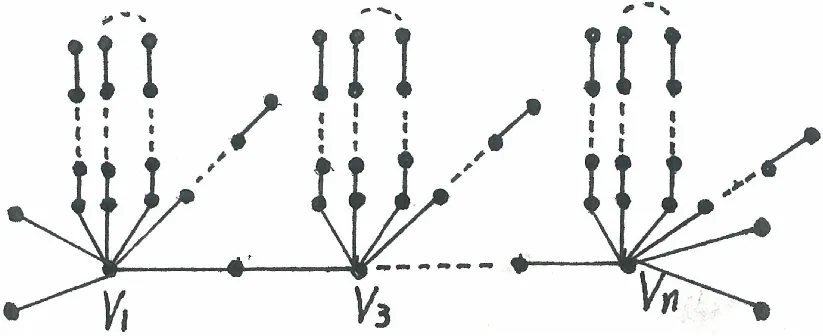
图3 图

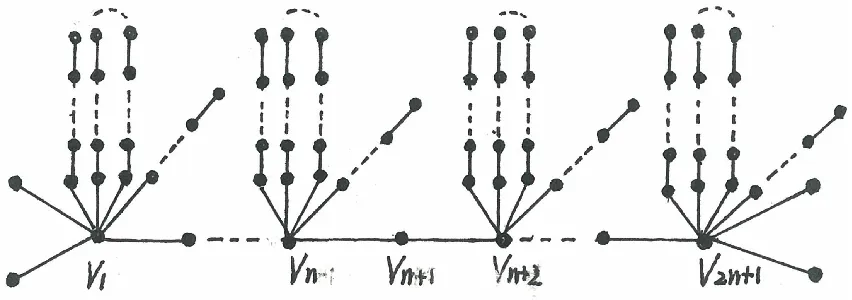
图4 图

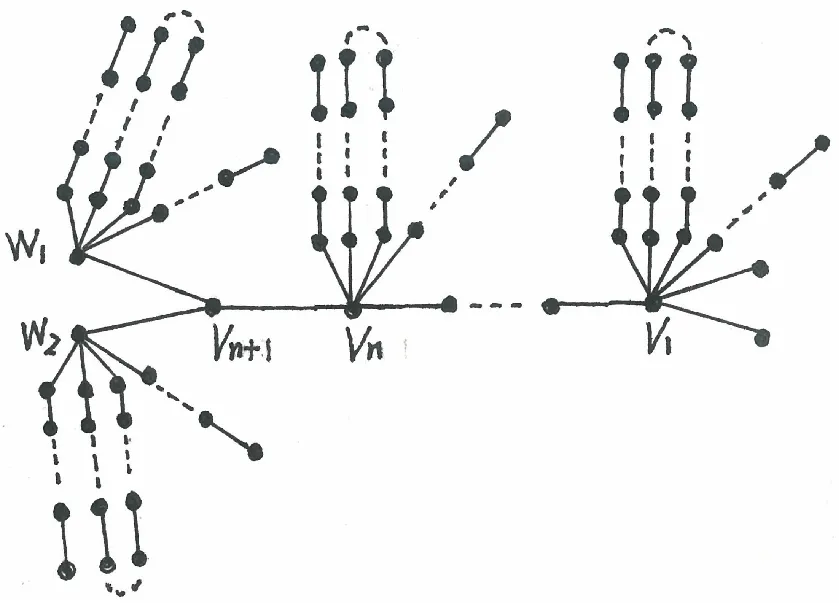
图5 图ΨT(2δ,(λ+1)+2)

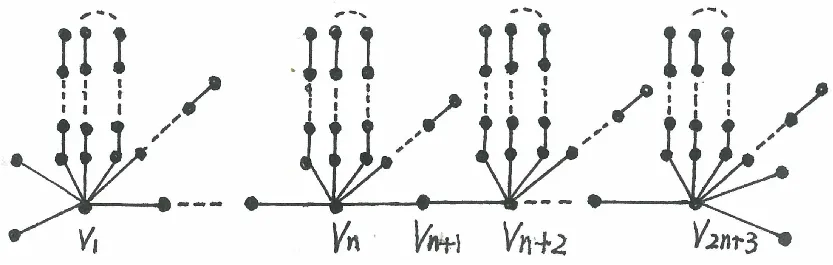
图6 图

引理3.1设m(≥3)是任意自然数，∀r∈N,r≥1，则有

(7)

(8)

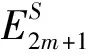
xh(Pm-1)h(Pm)=h(Pm)[xh(Pm)+xh(Pm-1)]+xh(Pm-1)h(Pm)=xh(Pm)[h(Pm)+2h(Pm-1)]

故(7)式成立；

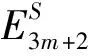
xh(Pm-1)h(Pm)h(Pm+1)=h(Pm+1)·

xh(Pm)[h(Pm)+2h(Pm-1)]+

xh(Pm-1)h(Pm)h(Pm+1)=

xh(Pm)h(Pm+1)[h(Pm)+3h(Pm-1)]

即(8)式也成立。

引理3.2设m(≥3)是任意自然数，∀r∈N,r≥1，δ=(r+1)m+r，则有

xh(Pm)hr-1(Pm+1)[h(Pm)+(r+1)h(Pm-1)]

(9)

证明如图3.1所示,对自然数r≥1作数学归纳法：当r=1,2时，由(7)和(8)两式知公式成立；假定公式对r-1成立，即

根据(12)式及归纳假定，我们有

xh(Pm-1)h(Pm)hr-1(Pm+1)=h(Pm+1)·

xh(Pm)hr-2(Pm+1)[h(Pm)+rh(Pm-1)]+

xh(Pm-1)h(Pm)hr-1(Pm+1)=

xh(Pm)hr-1(Pm+1)[h(Pm)+rh(Pm-1)]+

xh(Pm-1)h(Pm)hr-1(Pm+1)=

xh(Pm)hr-1(Pm+1)[h(Pm)+(r+1)h(Pm-1)]

由数学归纳法原理知，公式(9)对于任意自然数r都成立。

我们定义顶点数记号:λ=n+2-1(n+1)δ,则有

(n-2)+2-1(n-1)δ=n+2-1(n+1)δ-2-δ=λ-2-δ

2λ+1=(2n+1)+(n+1)δ,2λ+3+δ=(2n+3)+(n+2)δ

注意到δ=(r+1)m+r，λ-2-δ=(n-1)+2-1nδ,则由上式可知(10)式成立；

引理3.3设n(≥3)是奇数，m≥3,r≥1，δ=(r+1)m+r,λ=n+2-1(n+1)δ,则有

h(Pm-1)hr(Pm+1)h(ΨK(1,λ-2-δ))]

(11)

2h(Pm-1)hr(Pm+1)h(ΨK(1,λ-2-δ))]

(12)

证明(ⅰ)如图3.2所示，在图ΨK(1,n+2-1(n+1)δ)中取边e=V1W1,则由引理2.3和引理2.4，并注意到λ=n+2-1(n+1)δ，λ-2-δ=(n-2)+2-1(n-1)δ，我们有

h(Pm-1)hr(Pm+1)h(ΨK(1,λ-2-δ))]

故(11)式成立；

(ⅱ)如图3.2所示，在图ΨK(2,n+2-1(n+1)δ)中均取边e=V1W1,由引理2.3和引理2.4及(11)式，并注意到λ=n+2-1(n+1)δ，λ-2-δ=(n-2)+2-1(n-1)δ，我们有

即(12)式也成立。

引理3.4设n(≥3)是奇数，m≥3,r≥1，δ=(r+1)m+r,λ=n+2-1(n+1)δ,则有

(13)

(14)

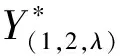
由此可知(13)式成立；

=x[xh(ΨK(2,λ))+

故(14)式也成立。

引理3.5设n(≥3)是奇数，m≥3,r≥1，δ=(r+1)m+r，λ=n+2-1(n+1)δ,则有

xh(Pm-1)hr(Pm+1)h(ΨK(2，λ))

(15)

(ⅱ)h(ΨT(2δ,(λ+1)+2))=

2xh(Pm-1)hr(Pm+1)h(ΨK(2，λ))]

(16)

证明(ⅰ)当n为奇数时，n+1为偶数，如图3.5所示，在图ΨT(δ,λ+1+δ)中取边e=w1Vn+1，由引理2.3和引理2.4，即得

xh(Pm-1)hr(Pm+1)h(ΨK(2，λ))

这里δ=(r+1)m+r，λ=n+2-1(n+1)δ,故(15)式成立；

(ⅱ)如图3.5所示，在图ΨT(2δ,λ+1+δ)中取边e=w1Vn+1，由引理2.3和引理2.4，即得

xh(Pm-1)hr(Pm+1)h(ΨK(2，λ))+

xh(Pm-1)hr(Pm+1)h(ΨK(2，λ))]=

2xh(Pm-1)hr(Pm+1)h(ΨK(2，λ))]

这里δ=(r+1)m+r，λ=n+2-1(n+1)δ,故(16)式成立。

引理3.6设n(≥3)为奇数，r≥1，δ=(r+1)m+r，λ=n+2-1(n+1)δ,则有

(17)

2xh(Pm-1)hr(Pm+1)h(ΨK(2,λ))]

(18)

证明(ⅰ)如图3.4所示，当n为奇数时，n+1为偶数，则d(Vn)=r+3,d(Vn+1)=2,

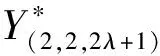
这里δ=(r+1)m+r，λ=n+2-1(n+1)δ,λ-2-δ=(n-2)+2-1(n-1)δ，故(17)式成立；

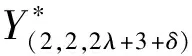
xh(Pm-1)hr(Pm+1)h(ΨK(2,λ))]=

xh(Pm-1)hr(Pm+1)h(ΨK(2，λ))+

xh(Pm-1)hr(Pm+1)h(ΨK(2,λ))]=

2xh(Pm-1)hr(Pm+1)h(ΨK(2,λ))]

设k是任意自然数，q是奇数，2≤r∈N,δ=(r+1)m+r，我们引入图的顶点记号

λk=(2kq-1)+2k-1qδ,容易推知λ1=(2q-1)+qδ，λk=2λk-1+1(k≥2)

设n是形如n=2k-1q-1的奇数，注意到λk=(2kq-1)+2k-1qδ，则计算可得

2λ+1=(2n+1)+(n+1)δ=(2kq-1)+2k-1qδ=λk

(19)

λ=n+2-1(n+1)δ=(2k-1q-1)+2k-2qδ=λk-1

(20)

4 因式分解定理

定理4.1设r(≥1)是任意自然数，m∈N,m≥3，，δ=(r+1)m+r，则有

(21)

(22)

证明对于∀r∈N,r≥1,m≥3，注意到h(K1)=x，由引理2.5、(13)和(6)两式，即得

xr+1[h(Pm)+(r+1)h(Pm-1)]=

h(Pm)hr-1(Pm+1)h(Ψ(r+1),m)

即(21)式成立；根据(21)式及引理2.5，容易推知(22)成立。

定理4.2设n(≥3)为奇数，r≥1，δ=(r+1)m+r，λ=n+2-1(n+1)δ,则有

(23)

(24)

证明(ⅰ)若n(≥3)为奇数时，注意到δ=(r+1)m+r，λk=(2kq-1)+2k-1qδ，由引理2.5、(17)和(14)两式，即得

x2h(ΨK(2,λ))[h(ΨK(2,λ))+

这里λ=n+2-1(n+1)δ，λ-2-δ=(n-2)+2-1(n-1)δ,故(23)式成立。

(ⅱ)根据引理2.4及(23)式，立即推知(24)式也成立。

把(19)和(20)两式依次代入(23)和(24)两式，我们有如下的

定理4.3设∀k∈N，q是奇数，r≥1，λk=(2kq-1)+2k-1qδ,则有

(25)

(26)

定理4.4设∀k∈N,q(≥3)是奇数，λk=(2kq-1)+2k-1qδ，δ=(r+1)m+r，则有

(27)

(28)

证明(ⅰ)对自然数k≥2作数学归纳法：当k=2时，由(25)式易推知

此时(35)式成立：假定结论对于k-1成立，对于k的情形，由引理2.5、(25)式及归纳假定即得

由此可知当k时结论也成立，故由数学归纳法原理知，对于任意的自然数k≥2，(27)式成立；

(ⅱ)根据引理2.4及(27)式，立即推知(28)式也成立。

定理4.5设n(≥3)为奇数，r≥1，δ=(r+1)m+r，λ=n+2-1(n+1)δ,则有

(29)

ΨT(2δ,(λ+1)+2))

(30)

证明(ⅰ)若n(≥3)为奇数时，注意到δ=(r+1)m+r，λ=n+2-1(n+1)δ，由引理2.5、(18)和(16)两式，即得

2xh(Pm-1)hr(Pm+1)h(ΨK(2,λ))]=

这里δ=(r+1)m+r，λ+1=(n+1)+2-1(n+1)δ,故(29)式成立;

(ⅱ)根据引理2.4及(29)式，立即推知(30)式也成立。

定理4.6设n(≥3)为奇数，r≥1，δ=(r+1)m+r，λ=n+2-1(n+1)δ,则有

h(Pm)hr-1(Pm+1)h(Ψ(r+1),

(31)

(32)

证明(ⅰ)若n(≥3)为奇数时，注意到δ=(r+1)m+r，λ=n+2-1(n+1)δ，以及λ+1=(n+1)+2-1(n+1)δ，由引理2.5、(29)和(21)两式，即得

故(31)式成立;

(ⅱ)根据引理2.4及(31)式，立即推知(32)式也成立。

5 图的色价性分析

在给出几类图的伴随分解的基础上，我们来讨论这些图色等价性。

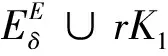
证明根据(28)式知

定理5.2设n(≥3)为奇数，r≥1，δ=(r+1)m+r，λ=n+2-1(n+1)δ,则图簇

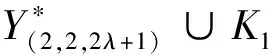
证明根据(24)式知

仿此，根据定义2.2和引理2.2以及(26)、(28)、(30)、(32)等四个公式，同法可证如下的几个结论：

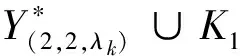
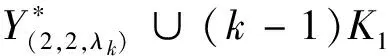
定理5.5设n(≥3)为奇数，r≥1，δ=(r+1)m+r，λ=n+2-1(n+1)δ,则图簇

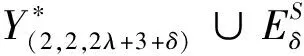
定理5.6设n(≥3)为奇数，r≥1，δ=(r+1)m+r，λ=n+2-1(n+1)δ,