一类微分差分方程的解与其位移分担值的唯一性
2022-01-27麦泽坤刘志学
麦泽坤,刘志学
(北京邮电大学 理学院 北京 100876)
1 引言与主要结果
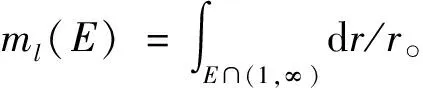
微分差分方程在物理,生物,经济,金融等领域具有广泛应用。近些年,随着复域方程以及Nevanlinna理论差分模拟的发展,微分差分方程引起了许多学者的关注[2-8]。徐玲等[9]研究了Fermat型微分差分方程的整函数解,他们得到
定理A设c为非零复数,p(z)为非零多项式。则Fermat型微分差分方程
f′(z)2+f(z+c)2=p(z)
的任意整函数解必形如
其中p(z)≡p1(z)p2(z),p1(z)和p2(z)均为多项式,而且p(z)和h(z)仅满足下面两种情况之一:
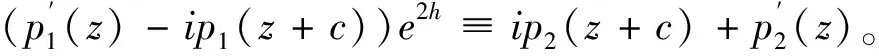
(ⅱ)如果h(z)为非常数的整函数,那么h(z):≡±iz+B,且c=kπ,k为任意整数。
1992年Quispel,Capel和Sahadevan[10]研究得到Kac-Van Moerbeke微分差分方程
可退化为
w(z)[w(z+1)-w(z-1)]+aw′(z)=bw(z)
此后许多研究工作均在此方程的基础上展开。Halburd和Korhonen[11]研究了一类微分差分方程解的存在性,他们得到
定理B假设f(z)为方程
(1.1)
的超越亚纯解,其中a(z)为有理函数,P(z,f(z))和Q(z,f(z))为f(z)的多项式,系数为z的有理函数,且R(z,f(z))为f(z)的不可约有理函数。若ρ2(f)<1,则有
degw(P)=degw(Q)+1≤3
或者
degw(R)≤1。
张然然和黄志波[12]研究了方程(1.1)的整函数解存在的条件以及整函数解的性质,得到:
定理C假设方程(1.1)存在超越整函数解f(z)满足ρ2(f)<1,R(z,f(z))为f(z)的不可约有理函数,则方程(1.1)退化为
或者
其中a0(z),a1(z),a2(z)为有理函数。
在本文中,我们将研究以下方程
(1.2)
的亚纯解的唯一性。
亚纯函数的唯一性理论是复分析的重要研究方向,主要研究亚纯函数在涉及分担值情形下是否唯一[13]。为了方便叙述,我们先介绍IM分担值和CM分担值的定义。
定义1.1设f(z)和g(z)为两个非常数亚纯函数,a为复平面上任意复数。若f(z)-a与g(z)-a具有相同的零点集,则称f(z)和g(z)IM分担值a;若f(z)与g(z)具有相同的极点集,则称f(z)和g(z)IM分担值∞。
定义1.2设f(z)和g(z)为两个非常数亚纯函数,a为复平面上任意复数。若f(z)-a与g(z)-a的零点相同,且每个零点的重数相同,则称f(z)和g(z)CM分担值a;若f(z)与g(z)的极点相同,且每个极点的重数相同,则称f(z)和g(z)CM分担值∞。
1926年,Nevanlinna通过引入亚纯函数的特征函数概念,建立了第一基本定理和第二基本定理,同时得到了以下唯一性理论中的经典结果。
定理D(五值定理[14])设f和g为两个非常数亚纯函数,ai(i=1,2,3,4,5)为扩充复平面中5个互相判别的复数。若f和gIM分担ai,则在整个复平面上有f≡g。
定理E(四值定理[15])设f和g为两个非常数亚纯函数,ai(i=1,2,3,4)为扩充复平面中4个互相判别的复数。若f和gCM分担ai,则在整个复平面上有f≡g,或者f是g的Möbius变换。
李玉华和乔建永[16]研究了亚纯函数分担5个小函数的情形,对Nevanlinna五值定理做了精确拓广。Laine和Korhonen[17]等人研究了亚纯函数与其位移在涉及分担值情形下的唯一性,结论如下所示:
定理F设f(z)为有限级亚纯函数,a1、a2、a3是关于f(z)的三个不同的周期为c的小函数。如果f(z)与f(z+c)CM分担a1、a2,IM分担a3,则在整个复平面上有f(z)≡f(z+c)。
本文考虑方程(1.2)的有限级超越亚纯解与其平移分担值的唯一性问题,并得到了下面的定理:
定理1.1假设f(z)为方程(1.2)的有限级超越亚纯解,α(z)、β(z)为非常数有理函数。当f(z)与f(z+c)CM分担a1、a2时(a1、a2∈{0}),如果f(z)只有有限多个零点或者f(z)有无限多个零点且均为单零点,则f(z)≡f(z+c)。
推论1.1假设f(z)为方程(1.2)的有限级超越亚纯解,α(z),β(z)为非常数有理函数。当f(z)与f(z+c)CM分担a1、∞时(a1∈{0}),如果f(z)只有有限多个零点或者f(z)有无限多个零点且均为单零点,则f(z)≡f(z+c)。
定理1.2假设f(z)为方程(1.2)的有限级超越整函数解,α(z)(α(z)≢0),β(z)为有理函数。如果f(z)与f(z+c)CM分担a1(a1∈{0}),则f(z)≡f(z+c)。
2 重要引理和基本记号
引理2.1([18])假设f(z)为一个有穷级亚纯函数,则对于任意c∈{0},有
引理2.2([2])设c∈,f(z)是一个亚纯函数,ρ(f)<∞并且Δcf(z)≢0。设q≥2,亚纯函数a1(z),…,aq(z)是f(z)不同的周期为c的小函数,即
max{T(r,a1),…,T(r,aq)}=o(T(r,f))=S(r,f)
满足ak∈S(f),k=1,…,q,则有
其中Npair(r,f)=2N(r,f)-N(r,Δcf)+N(r,1/Δcf),Δcf=f(z+c)-f(z)。
引理2.3([18])假设f(z)为一个有限级亚纯函数,c为一个非零实数,则f(z)满足
T(r,f(z+c))=T(r,f(z))+S(r,f),
N(r,f(z+c))=N(r,f(z))+S(r,f)
引理2.4([19])设h(z)为非常数亚纯函数满足
令f=a0hp+a1hp-1+…+ap,g=b0hq+b1hq-1+…+bc为h(z)的多项式,系数a0,a1,…,ap,b0,b1,…,bq为h(z)的小函数,满足a0b0ap≢0。如果q≤p,则有
3 定理的证明
3.1 定理1.1的证明
假设f(z)≢f(z+c),由条件f(z)只有有限多个零点或者f(z)有无限多个零点且均为单零点,分类讨论。
情形1f(z)有无穷多个单零点时,定义
E*={z|f(z)=0}{{z|α(z)=0,∞}∪{z|β(z)=0,∞}}
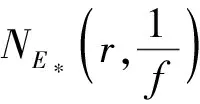
(3.1)
将任意z0∈E*代入方程(1.2)有
可以看出则z=z0+1和z=z0-1中至少有一个为f(z)的极点。
(ⅰ)若z=z0+1和z=z0-1均为f(z)的极点,则代入方程(1.2)有
从上式中可以看出z=z0+2和z=z0-2也为f(z)的极点。不难得出在充分大时有
结合(3.1)式有
(3.2)
利用引理2.2有
(3.3)
由分担值条件f(z)与f(z+c)CM分担a1,a2可知,当f(z)分别取a1,a2时,f(z+c)也分别取a1,a2,且重数相同。而f(z+c)-f(z)还可能有除去a1,a2以外的其他零点,所以
(3.4)
由(3.3)式和(3.4)式,结合引理2.3整理得
(3.5)
通过(3.2)式有T(r,f) (ⅱ):若z=z0+1和z=z0-1中一个为f(z)的极点,不失一般性,我们假设z=z0+1为f(z)的极点(z=z0-1为f(z)的极点的情况类似),则将z=z0+1代入方程(1.2)可知z=z0+2为f(z)的极点,由此可以得出在r充分大时有 由(3.1)式有 (3.6) 结合(3.5)式有T(r,f) 情形2f(z)只有有限多个零点,可以得到在r→∞时, 通过前面的证明,结合(3.5)式有T(r,f)=S(r,f),显然是矛盾的。 假设f(z)≢f(z+c)。由定理1.1的证明可知方程(1.2)的有限级超越亚纯解的零点数量满足(3.2)式和(3.6)式,即在r充分大时有 (3.7) (3.8) 通过分担值条件可以得到,g(z)与g(z+c)CM分担0,1/a1。当g(z)分别取0,1/a1时,g(z+c)也分别取0,1/a1且重数相同。而g(z+c)-g(z)还可能有除去0,1/a1以外的其他零点,所以有 (3.9) 由(3.8)式和(3.9)式,结合引理2.3和引理2.4整理得 T(r,g)≤N(r,g)+S(r,g) 所以N(r,g)=T(r,g)+S(r,g),由第一基本定理,即有 结合(3.7)式,在r充分大时,有T(r,f) 假设f(z)≢f(z+c)。因为f(z)为方程(1.2)整函数解,则由之前的讨论可知f(z)的零点有限,即在r充分大时,f(z)满足 由f(z)与f(z+c)CM分担a1可知,存在多项式H(z)使得 (3.10)接下来对eH(z)分类讨论。 情形1若eH(z)≡1,则证得f(z)≡f(z+c)。 情形2若eH(z)≢1,H(z)为常数,则由(3.10)式有 eH(z)f(z)-f(z+c)=a1eH(z)-a1 整理得 对等式两边求其均值函数,有 (3.11) 情形三:若H(z)为非零多项式,则利用引理2.4可知 通过(3.11)式有3.2 推论1.1的证明
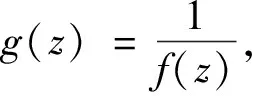
3.3 定理1.2的证明
