高中数学解题的基本策略及其应用

◎周泽汀

(吉林师范大学,吉林 长春 130000)

在学习数学的过程之中，解题训练是十分重要的.不少学生不因数学知识为难，而因解答问题而为难.对于难度较大的高中数学知识，掌握相应的数学解题策略是学生学好数学，提升数学学习效率必不可少的条件之一.从本质上说，数学解题策略是一种特殊的学习活动，是由数学基础知识、基本技能、基本数学思维方法和数学运用能力相互作用、相互融合形成的，掌握数学解题策略不仅能够锻炼学生的数学思维，还能够培养学生对数学的兴趣，提高学生解题的效率，下面笔者就为大家介绍一下常用的数学解题策略.

1 审题策略

从本质上讲，解决数学问题的过程其实就是对题中条件进行加工重组的过程.所以，我们在解题之前，必须精审题意，严把条件，对于题目中的每个条件都要领会全面，并根据题中条件制定解题策略，这样才能高效的解题.审题策略对于解决高中数学问题是十分重要的，只有深入地理解题目中所给条件的内在含义才能在答题过程中找准关键点，理清思路，从而有效地解答问题.审题策略主要包含以下两点：一是要全面收集题目信息，包括条件中都有什么数量关系，每个条件代表着什么意义，大致的解题方向是什么，这些条件都与哪些知识是相关的，等等；二是要在读懂题目的基础上深刻挖掘题目中所隐含的条件，必要时可以通过符号语言或者是数学形式的转换来寻找.

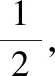
2 分析策略

分析策略是常用的数学解题策略之一.因为不同的数学问题有着不同的特征，故有着不同的解题方法.有些问题可以运用定义定理直接解决，对于这类问题要抓住题目中的形式化语言，因为这些形式化语言往往暗示着某种运算的法则.有些问题则需要从题目中的某个部分着手，然后过渡到整个问题，进而解决该问题.对于这种问题，教师先要引导学生建立各个条件之间的联系，然后用推理的方法解决该问题.还有一些问题是不能够直接找到解决方法的，而是需要通过数形结合来解答，即建立图与数之间的对应关系，画出图像会使问题更加直观地呈现在我们面前，更便于解答.此外，我们还要巧妙地运用数学符号，将数学语言符号化，这样做能够使题目中的条件更加清晰直白，便于理解.分析策略就是抓住题中的提示和问题的特征，并就这些信息进行分析和思考，从而找到解决问题的正确途径.

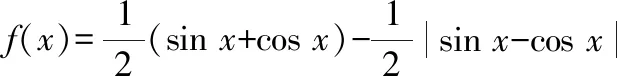
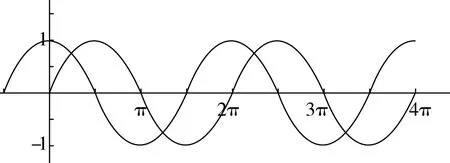
图1

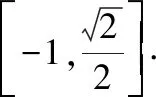
3 化归策略

化归策略指用转化的思想来解决数学问题的策略.转化思想就是指通过观察，分析，类比等思考过程，然后选择恰当的方法变换，从而实现将未知转化为已知的目的.高中数学涉及的知识和问题都有内在的联系，并且在一定条件下可以相互转化.对于未知问题的解答，可通过建立与已知问题的内部联系，运用转化的思想将未知问题转化成已知的或与已知问题相类似的问题，从而使原来的问题获得解答.化归策略所渗透思想的是转化思想，这也是学习迁移理论在数学解题方面的拓展与应用.运用化归策略需要注意的点是对于待解决的问题要依照题目所要求的方向进行转化，通常是由复杂到简单，由高级到低级，由抽象到具体.将复杂的问题转化成某种特殊形式，可以引发学生的联想，促进问题的快速解决.

4 回归策略

我们都知道书本上的知识是解题的基础，主要包括一些数学定义，定理，法则等.而一些复杂的难以解决的数学问题，其实是对课本知识的拓展与运用.正所谓万变不离其宗，想在解决复杂的高中数学问题时，就要回归教材，从书本中找到相应的考点和知识点，有些数学问题看上去难以解决，实则是几个知识点串联在一起而已，还有一些数学题目题型非常新颖，表述也很抽象，给解答设置了很多的障碍，但其本质上是某个定义或定理的延伸，是其形式的转换，而这些定义定理自然都是来源于书本教材的.所以，为了提高学生解决数学问题的能力，我们要回归教材，熟读书本，加深对定义和定理的理解，能够将复杂的数学问题回归到比较基础的数学知识之中，这样才能够获得明确的解题思路.

例动点M与两定点A(-1,0)，B(2,0)构造三角形MBA，且∠MBA=2∠MAB，设动点M的轨迹为C.如图：

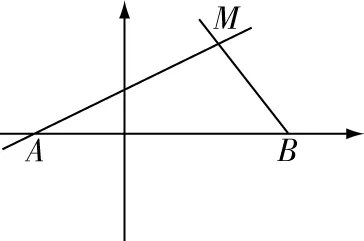
(1)求轨迹C的方程；

5 答题策略

答题策略在数学解题中应用十分广泛.我们都知道，要想提高数学解题能力，就必须夯实基础的数学知识，把握重点内容，所以必要的数学训练也是必不可少的.在平时的解题训练之中，学生对于错的题目要进行及时的总结和归纳，找出错误的原因和相应的知识点，对理解薄弱的地方，要进行针对性练习.不仅如此，在正式的考试中，学生还要学会放松自己的心情，用平和的心态去完成每一道题目.答题的顺序要由浅入深，由易到难，这样有利于保持平稳的心态，因为后面难度较大的题目都是按照采分点得分的，如果经过深思熟虑仍不能解决，那就尽自己所能，取得力所能及的分数.同时，学生也要善于把控时间，合理安排填空、选择，以及每道大题的时间，从而提高答题的效率.

例求y=cosx2+sinx的值域.

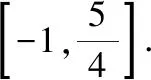
6 增设策略

我们在解决高中数学问题时，可能遇到运用题目中原有的条件无法解决问题的情况，在这个时候为了结局问题，可以在原条件的基础上进行有效的增设，这种解题策略叫作增设策略.所谓增设是指在原题意的基础上增加一些可用的条件，例如在解决几何问题时加入的辅助线、辅助角、在解决代数问题时所加入的参数等等，增设的关键在于恰到好处地引进，有效的增设可以给答题者提供更为清楚的解题脉络，帮助学生高效率地解决问题.增设既能有效地沟通已知之间的联系也能有效地沟通未知与已知的联系，从而刻画事物之间的内在规律，答题者可以以这些增设为媒介，对问题加以分析和综合，从而找到解决问题的方法.

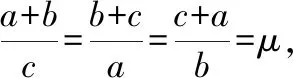
然后再将其化简为包含多个未知量的方程组的形式.

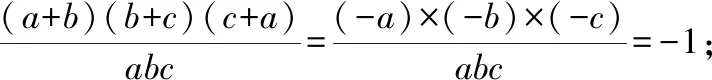
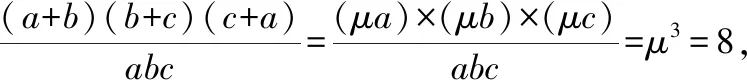
7 结 语

美国心理学家威廉·詹姆斯曾说过这样一句话：“解题是最突出的一类特殊的自由思维.”不仅如此，解题还是数学学习的众多组成部分之一，也是进行数学训练所要达到的目标.多种有效的解题策略不仅能够帮助学生解决实际的数学问题，还能激起学生对数学学习的兴趣.由此可见，掌握一些解题策略对于学生来说是十分必要的.但是，如果想更好地发挥数学解题策略的优势，就需要学生将基础知识的学习和数学思维的训练结合起来，并在实践中不断地归纳和总结，只有不断扩充自己的知识结构才能够取得更好的学习效果.