B2到B9的某类5次逆紧全纯映照

◎彭 勃 王丽欣

(吉林师范大学，吉林 四平 136000)

1906年Hartogs发现，球环{(z1,…,zn):r2<|z1|2+…|zn|22)上的逆紧全纯映照是线性嵌入[2]；1982年，J.Faran对B2→B3的部分逆紧全纯映照进行了分类，证明具有三次连续可微边界的B2→B3的逆紧全纯映照等价于Whitney映照或者另一种简单映照[3]；1999年，X.Huang证明出具有二次连续可微边界的Bn→BN(n>1,N≤2n-2)上的逆紧全纯映照等价于线性嵌入[4]；2006年，Z.Chen，S.Ji和D.Xu研究了B2→BN上的二次逆紧全纯有理映照的分类结果[5]；2009年，S.Ji和Y.Zhang证明了任意B2→BN上的二次逆紧全纯有理映照等价于B2→B5上的二次逆紧全纯有理映照[6]，至此，B2→BN上的二次逆紧全纯有理映照的分类问题得到解决.因此，构造出更高次的逆紧全纯有理映照是必要的.

1 定义

1.1 有界域[7]

1.2 单位球[7]

设a=(a1,…,an)∈n,ρ>0，称是以a为中心，ρ为半径的球.当a=0,ρ=1时，称是单位球，称∂Bn={(z1,…,zn)∈n:|z1|2+|z2|2+…+|zn|2=1}为相应的球面.

1.3 全纯映照[8]

1.4 逆紧映照[9]

设X,Y是拓扑空间，连续映照f:X→Y是逆紧的，当且仅当对任意紧集K⊂Y，f-1(K)在X中是紧的.

1.5 逆紧全纯映照[9]

设Ω,Ω′是有界域，映照f:Ω→Ω′是全纯的，且是逆紧的，则f:Ω→Ω′是逆紧全纯的.

1.6 逆紧全纯有理映照[9]

1.7 张量积[8]

2 引理

引理2.1[8]设Ω⊂n，f:Ω→N和g:Ω→BM是逆紧全纯映照，f的值域可直和分解为BN=A⊕A⊥，且dimA=a(1≤a≤N-1),dimA⊥=N-a,dimN=N，dimM=M，那么映照E(A,g)(f)=(fA⊗g)⊕fA⊥为Ω到a(M-1)+N的逆紧全纯映照.

证明显然E是全纯的.接下来证明E是逆紧的，令|z|→1，则|g|2→1，从而|E|2=|fA|2|g|2+|fA⊥|2与|fA|2+|fA⊥|2=|f|2有相同的极限.又因为f是逆紧的，所以|E|2→1，因此E是逆紧的.

引理2.2[3]设f:B2→B3是一个具有三次连续可微边界的逆紧全纯映照，则f等价于下述映照的其中之一：

引理2.3[10]若f:B2→B4是一个单项式逆紧映照，则f等价于下列映照之一：

3 构造

根据引理2.1，利用B2到B3和B2到B4的逆紧全纯映照，我们构造出部分B2到B9的次数为5的逆紧全纯映照.

情形1：设f(z,w)=(z,zw,w2)，选取由(1,1,0)生成的子空间作为A来分解f，应用上述B2到B4的逆紧全纯映照的显式表达式，利用映照E(A,g)(f)=(fA⊗g)⊕fA⊥进行计算，得到

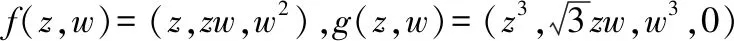
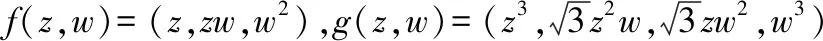
(3)当f(z,w)=(z,zw,w2),g(z,w)=(z3,z2w,zw,w)时，

E(A,g)(f)=u3(z,w)=(z4,z3w,z2w,zw,z4w,z3w2,z2w2,zw2,w2);

(4)当f(z,w)=(z,zw,w2),g(z,w)=(z2,z2w,zw2,w)时，

E(A,g)(f)=u4(z,w)=(z3,z3w,z2w2,zw,z3w,z3w2,z2w3,zw2,w2);

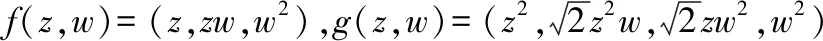
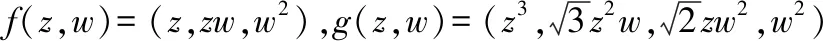
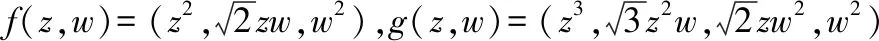
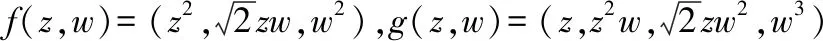
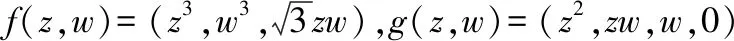
情形4：设f(z,w)=(z,w,0)，选取由(1,1,0)生成的子空间作为A来分解f，应用上述B2到B4的逆紧全纯映照的显式表达式，利用映照E(A,g)(f)=(fA⊗g)⊕fA⊥进行计算，得到

由于表达式较多，下面选取u1和v1进行证明，其它的同理可证.

证明只需验证这一映照是∂B2到∂B9上的映照，即证明当|z|2+|w|2=1时，有|E|2=1.

=|z|8+3|z|4|w|2+|z|2|w|4(|w|2+|z|2)+2|z|4|w|4+|z|2|w|8+|z|8|w|2+|w|4

=|z|8+2|z|4|w|2+|z|2|w|2(|z|2+|w|2)+2|z|4|w|4+|z|2|w|8+|z|8|w|2+|w|4

=|z|8+2|z|4|w|2+2|z|4|w|4+|z|2|w|8+|z|8|w|2+|w|2(|z|2+|w|2)

=|z|8+|z|4|w|2(|z|2+|w|2)+|z|4|w|2+2|z|4|w|4+|z|2|w|8+|z|8|w|2+|w|2

=|z|6(|z|2+|w|2)+3|z|4|w|4+|z|4|w|2+|z|2|w|8+|z|8|w|2+|w|2

=|z|4(|z|2+|w|2)+3|z|4|w|4+|z|2|w|8+|z|8|w|2+|w|2

=|z|4+2|z|4|w|4+|z|4|w|4(|z|2+|w|2)+|z|2|w|8+|z|8|w|2+|w|2

=|z|4+2|z|4|w|4+|z|6|w|2(|z|2+|w|2)+|z|2|w|6(|z|2+|w|2)+|w|2

=|z|4+|z|4|w|2(|z|2+|w|2)+|z|2|w|4(|z|2+|w|2)+|w|2

=|z|4+|z|2|w|2(|z|2+|w|2)+|w|2

=|z|2(|z|2+|w|2)+|w|2

=|z|2+|w|2=1

同样的方法，可以验证v1：

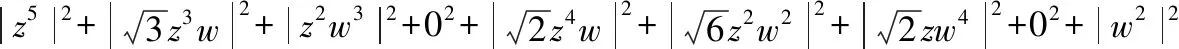
=|z|10+3|z|6|w|2+|z|4|w|6+2|z|8|w|2+6|z|4|w|4+2|z|2|w|8+|w|4

=|z|8(|z|2+|w|2)+3|z|4|w|2(|z|2+|w|2)+|z|2|w|6(|z|2+|w|2)+|z|8|w|2+|z|2|w|8+3|z|4|w|4+|w|4

=|z|8+3|z|4|w|2+|z|2|w|6+|z|8|w|2+|z|2|w|8+|z|4|w|4(|z|2+|w|2)+2|z|4|w|4+|w|4

=|z|8+3|z|4|w|2+|z|2|w|4(|w|2+|z|2)+|z|6|w|2(|z|2+|w|2)+|z|2|w|6(|z|2+|w|2)+|z|4|w|4+|w|4

=|z|8+3|z|4|w|2+|z|2|w|4(|z|2+|w|2)+|z|6|w|2+|z|2|w|6+|z|4|w|4+|w|4

=2|z|2|w|4(|z|2+|w|2)+|z|6(|z|2+|w|2)+3|z|4|w|2+|w|4

=2|z|2|w|4+|z|6+3|z|4|w|2+|w|4

=2|z|2|w|2(|z|2+|w|2)+|z|4(|z|2+|w|2)+

|w|4

=2|z|2|w|2+|z|4+|w|4

=|z|2(|w|2+|z|2)+|w|2(|z|2+|w|2)

=|z|2+|w|2=1