密集阵列波导光栅的偏振相关波长优化分析

吴瑶，郑煜，何浩，刘志杰，段吉安

(中南大学高性能复杂制造国家重点实验室，湖南长沙，410083)

随着5G 网络时代的到来，物联网、大数据、云计算等网络技术得到飞速发展，光纤通信技术在信息技术领域的地位越来越重要，其应用逐步扩展到工业、军事及电力等领域[1]。在光纤通信技术中，波分复用系统(WDM)因其具有传播容量大、扩容方便、传播信号透明及成本低等特点，在光纤通信领域具有广阔的应用前景[2−3]。WDM中的密集波分复用系统(DWDM)在应用方面不仅增加了系统带宽，满足了人们日益增长的通信业务需求，而且还大大提高了通信系统的性能，因而成为了光纤通信领域的研究热点和首选技术[4]。其中，AWG 器件因具有损耗低、串扰小、均匀性好、集成度高等优越性能而成为DWDM核心器件——波分复用/解复用器[5−6]。此外，AWG还可以应用于调谐滤波器、波导光栅路由器和光分差复用器等[7]，在光纤通信领域的发展中具有非常重要的地位。

AWG 的偏振相关波长(PDW，用符号WPD表示)是衡量其光学性能的主要参数之一，WPD的优化对AWG 的性能有着重要的影响。WPD优化方法主要有应力释放槽法[8−9]、半波片法[10−11]、调节包层热膨胀系数法[12]及其他方法[13−14]等。其中，调节包层热膨胀系数法制备工艺简单，且不会降低器件的其他性能，适用于各种二氧化硅器件，是目前偏振补偿较实用的方法[15−17]。以往人们对波导热应力进行分析时所建立的模型较单一，并未与AWG器件真正结合，导致能优化单根波导WPD的方法并不能使整个AWG 器件的WPD减小，且并未给出优化WPD后AWG器件的具体制备工艺。

WPD主要因波导正交方向的热应力不同而引起，而衬底和包层的热膨胀系数不匹配是导致波导在正交方向产生热应力差的主要原因。本文采用石英基二氧化硅的工艺方法制备AWG器件，相对于传统的硅基二氧化硅AWG，石英基二氧化硅AWG 的石英衬底和二氧化硅包层热膨胀系数相同，可以有效减小AWG 的WPD[18]，但对于与平板波导连接处的阵列波导而言，由于波导之间的间距过小，使得连接部位处的波导正交方向的热应力差较大，WPD过大，从而影响整个AWG 的WPD。为此，本文利用有限元方法对与平板波导连接处的波导间距在1～5µm 范围内的阵列波导进行热应力分析，并据此提出调节相应波导包层的热膨胀系数的方案来优化WPD，旨在将整个AWG的WPD降至0.05 nm 以内，从而降低AWG 的偏振相关。调节包层的热膨胀系数主要通过向包层中掺入一定比例的氧化物，研究掺入氧化物的搭配比列，使包层的热膨胀系数在保证折射率不变的情况下满足要求。由于AWG中位于平板波导连接处的阵列波导的包层需要掺杂来提高热膨胀系数，而其他部位的波导不需要，因此，本文提出一种新工艺流程来实现AWG不同波导处包层的掺杂，由以上方法制备出低WPD的AWG器件。

1 WPD的理论分析

在制备AWG器件时，需要在沉积膜层后进行高温退火。由于AWG的衬底、包层及波导的热膨胀系数存在差异，波导在正交方向受到大小不等的热应力，由于光弹效应引起各方向上折射率不同，从而产生双折射现象，引起AWG的偏振相关性。在AWG 的光学性能指标中，通过WPD来反映AWG 偏振相关性的严重程度，其相关表达式如下[19]：

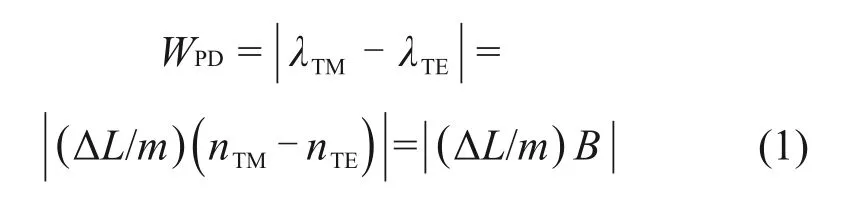
式中，λTE和λTM分别为TE和TM偏振态下的中心波长；nTE和nTM分别为TE和TM偏振态下的有效折射率；B为双折射系数；ΔL为相邻阵列波导长度差，m为衍射级数，ΔL/m为AWG的结构参数，在这里为定值。因此，要消除WPD，需减小双折射系数B，而产生B的根本原因是波导受到正交方向的热应力不同，其表达式为[13]

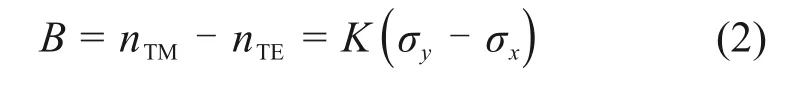
式中：K=3.43×10−12Pa−1，为波导的光致变色系数[20]；σx和σy分别为波导在水平方向(x方向)和垂直方向(y方向)受到的应力。

图1所示为薄膜沉积在厚膜上的结构示意图。在高温退火后，厚膜受到来自薄膜作用的水平方向(x方向)热应力σ1作用，其表达式为[21]

图1 多膜结构模型示意图Fig.1 Schematic diagram of multi-membrane structure model

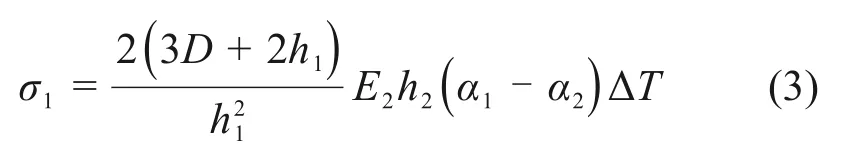
式中：h1和h2分别为厚膜和薄膜的厚度；D为计算应力点离两膜交界处的距离；E2为薄膜的弹性模量；α1和α2分别为厚膜和薄膜的热膨胀系数；ΔT为材料受到的温度变化量。薄膜受到的热应力σ2为

从上面分析可以看出薄膜和厚膜热应力的计算公式存在区别，因此，在使用热应力计算公式时，要先区别厚膜与薄膜，才能使用与之对应的计算公式。

2 波导模型的建立

石英基二氧化硅AWG的石英衬底与二氧化硅包层热膨胀系数相同，可以有效地减小波导正交方向的热应力差，减小WPD。AWG基本结构如图2所示。由于AWG中与平板波导连接处的阵列波导间距过小，会对波导垂直方向的热应力产生很大影响，而其他部位的波导间距很大，加上包层和衬底的热膨胀系数相同，所以，这些区域波导在正交方向上的热应力基本相同，WPD很小。此外，阵列波导数量多，其WPD增大会影响整个AWG 的WPD，为此，本文主要针对与平板波导连接处的阵列波导来建模并进行分析。模型的建立基于如下假设：1)热膨胀系数不随温度变化而变化；2)将整个系统的材料视为线弹性材料；3)波导在传播方向的长度为无限大，其变形量为常数，这可以将三维模型降为二维模型，提高模拟的工作效率。

图2 AWG基本结构Fig.2 AWG basic structure

石英衬底在制备中的厚度为525µm，而实际上，在器件达到稳态后对波导有重要影响的厚度非常小，因此，在保证结果误差很小的情况下，为提高仿真效率，设定模型中建立的石英衬底厚度为100µm。此外，模型计算区域不能太大，否则网格难以细分，仿真精度不够。根据AWG版图结构，按照比例建立计算区域(长×宽为500 µm×125µm)，阵列波导数为5 根。温度变化范围是从包层退火温度1100 ℃到室温22 ℃。模型结构示意图、各结构材料属性、模型结构参数分别如图3、表1和表2所示。

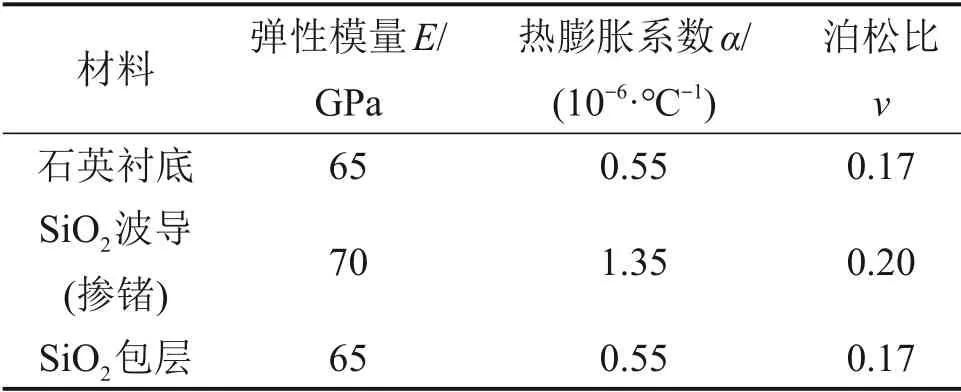
表1 模型材料属性Table 1 Model material properties

表2 模型结构参数Table 2 Model structure parameters

图3 二维模型局部示意图Fig.3 Partial schematic diagram of two-dimensional model

3 波导热应力分析

采用Comsol 软件对建立的波导模型进行热应力有限元仿真。设初始温度为1 100 ℃，衬底、包层及波导在此温度作用下，温度降低到室温22 ℃(高温退火)后达到稳态，而此时，衬底、包层及波导中会产生热应力。

图4和图5所示为基于有限元方法得出的波导热应力分析结果。从图4可见：由于波导的热膨胀系数大于衬底和包层的热膨胀系数，所以，高温退火后，波导的收缩量会大于衬底和包层的收缩量，衬底和包层会受到波导的压应力，而波导则会受到来自衬底和包层抵抗其收缩的作用力即拉应力作用。波导水平方向的热应力主要由波导上下界面的包层和衬底引起，左右界面处的包层对波导水平方向热应力影响较小。但由于波导间的包层宽度和热膨胀系数相对于波导来说都较小，所以，当波导收缩时，会带动波导间的包层一起收缩，波导对波导间的包层产生较小的压应力，同样，波导间包层也对波导产生较小的压应力。而波导带动波导间包层的收缩会使它们受到上下界面衬底和包层的拉应力作用，波导与波导间包层相互作用的压应力抵消部分拉应力，使得波导间包层和波导左右界面的压应力小于波导中心处的压应力。波导上下界面由于离包层和衬底较近，所以，受到的影响相对于波导中心处来说较大，使其受到的拉应力大于中心处拉应力。根据测量，波导中心处的水平方向压应力为5.7×107Pa，而根据式(4)计算得到的压应力为6.0×107Pa(由表2可知：波导横截面尺寸相对于包层和衬底厚度来说较小，因此可将波导视作薄膜，所以采用式(4)计算波导热应力，与测量值误差很小)。阵列波导垂直方向(y方向)热应力分析图如图5所示。波导受到垂直方向的热应力主要来自其左右界面间的包层，即波导间包层会对波导产生垂直方向的拉应力作用。由于波导间的包层厚度小，相对于波导横截面尺寸来说较小，因此波导间包层可视作薄膜，而波导相对于波导间包层来说则是厚膜，所以，波导的热应力采用式(3)计算，所得波导中心处的拉应力为1.30×107Pa，而测量值为1.56×107Pa，两者误差很小。通过式(4)计算得到波导间包层的压应力为5.60×107Pa，测量值为5.40×107Pa。此外，波导的左右界面离波导间包层越近，受到的影响越大，即拉应力越大。

图4 阵列波导水平方向(x方向)热应力分析图Fig.4 Analysis diagrams of thermal stress in horizontal direction(x direction)of arrayed waveguides

图5 阵列波导垂直方向(y方向)热应力分析图Fig.5 Analysis diagrams of thermal stress in vertical direction(y direction)of arrayed waveguides

以上基于有限元方法得出的应力结果和公式计算结果都接近，误差较小，说明所建立的模型是正确的。

通过对与平板波导连接处的阵列波导水平方向和垂直方向的热应力进行分析，发现虽然衬底和包层的热膨胀系数相同，但波导在正交方向受到的热应力不同，其主要原因是波导在不同热应力分析方向上所处的情况不同。在水平方向上，波导相对于上下界面的衬底和包层是薄膜，在垂直方向上，波导相对于侧面波导间的包层而言是厚膜，因此，由式(3)和(4)可知波导在2 个方向受到的热应力不同。

根据WPD计算公式，得出波导的WPD≥0.16 nm。为使波导在2 个方向的热应力相同，需降低WPD，以降低AWG的偏振相关波长。根据以上分析，主要有3种方案：1)增大波导间距，使波导间包层厚度相对于波导横截面尺寸来说更大；2)减小波导上下界面处的衬底和包层的厚度，使它们相对于波导横截面尺寸来说更小；3)增加波导包层的热膨胀系数，使波导在垂直方向的热应力增至与水平方向热应力一样大。方法1)和方法2)需要更改AWG 的结构，这会对AWG 的其他性能产生很大影响，而方法3)只需在沉积包层时掺杂来增加包层热膨胀系数即可，方法简单，效率高，可行性强，所以，本文采用方法3)来降低AWG的WPD。

4 波导的WPD优化

从上面分析可知，波导正交方向的热应力差和波导间距存在很大关系。与平板波导连接处的阵列波导间距随着远离连接处而呈线性增大。利用有限元热应力分析可得出波导间距与波导正交方向热应力及WPD的关系如图6所示(其中，d为波导间距，σx和σy分别为波导水平和垂直方向的热应力)。由于光场主要集中在波导中心处传播，所以，主要分析波导中心处的热应力。当衬底的热膨胀系数αSub与包层的热膨胀系数αClad相等，且为0.55×10−6/℃时，随着d增大，σx逐渐减小，σy逐渐增大，WPD逐渐减小并趋于0；而当d小于5µm时，WPD大于0.05 nm。为对波导的WPD进行更好优化，在d小于5µm的波导部分增加包层的热膨胀系数αClad，以减小d在1～5µm范围内波导的WPD，根据分析得出不同条件下波导间距d与WPD的关系如图7所示。

图6 αSub=αClad时，波导的WPD，σx及σy与波导间距d的关系Fig.6 Relationship among WPD,σx,σy and waveguide gap d at αSub=αClad

从图7中曲线1可见：随着d减小，要使波导的WPD为0 nm，所增加的αClad越大。而在制备工艺中，包层的沉积是同时进行的，以保证均匀沉积，也就是αClad不能渐变，即在d为1～5µm时，增加的αClad都是相同的。为使d在1～5 µm 范围内的波导WPD优化达到最佳，取此范围内增加的αClad为均值，即为2.42×10−6/℃。从图7中曲线2可知：当d在1～5 µm 范围内时，WPD均小于0.05 nm，这与d大于5 µm 且αClad=0.55×10−6/℃时的WPD一样(也是小于0.05 nm)，满足本文的设计要求。因此，为更好地优化波导的WPD，对d为1～5µm范围内的波导增加αClad至2.42×10−6/℃，其余部位波导的αClad保持为0.55×10−6/℃不变。

图7 不同条件下波导间距d与WPD的关系Fig.7 Relationship between waveguide gap d and WPD under different conditions

经过上述方法优化后的AWG，若其WPD与平板波导连接处的波导间距d为1～5µm 时的阵列波导(其优化后的包层折射率为αClad=2.42×10−6/℃)在d=1 μm和d=5 μm时的WPD都小于0.05 nm，则认为AWG中这部分的波导符合设计要求。AWG中除了与平板波导连接处的小间距(d为1～5µm)部位的阵列波导之外，其余部位的阵列波导间距d都大于0.5 μm，且相应的包层折射率αClad=0.55×10−6/℃，在此情况下，取d=5 μm。若WPD小于0.05 nm，则可认为AWG 中d大于0.5 μm 的区域波导也满足设计要求。在一般情况下，AWG 的工作环境范围为−40～80 ℃。采用高温退火工艺对波导进行处理以消除其残余应力后，考察以下3 种情况：1)d=1 μm，αClad=2.42×10−6/℃；2)d=5 μm，αClad=2.42×10−6/℃；3)d=5 μm，αClad=0.55×10−6/℃。在这3 种工况下，研究波导工作在−40～80 ℃环境下的WPD变化规律，得到工作温度与WPD的关系如图8所示。从图8可知：经过优化后的AWG，不论是在与平板波导连接处的波导间距d为1～5µm 的阵列波导部位，还是在d都大于5 μm 的其余部位的阵列波导，在工作温度范围内，波导的WPD均小于0.05 nm，说明设计满足要求。

图8 工作温度与WPD的关系Fig.8 Relationship between working temperature and WPD

5 工艺分析

5.1 掺杂分析

通过向与平板波导连接处的阵列波导包层中掺杂氧化物以增加此处包层的热膨胀系数，优化WPD。掺入的氧化物不仅要能增加包层的热膨胀系数，而且要维持包层的折射率不变，为此，向包层中掺入2种不同的氧化物。包层及掺杂氧化物的材料属性如表3所示。表3中，由于氧化物A和氧化物B的材料属性可根据选择掺入的氧化物而定，其中掺入的氧化物可以是五氧化二磷(P2O5)、三氧化二硼(B2O3)和二氧化锗(B2O3)等，具体地可根据工艺条件及需求进行选择与配比，因此，表3中的氧化物A和氧化物B的的材料参数(折射率n、热膨胀系数α、摩尔质量M、密度ρ)并没有具体给定，而是用相应的参数符号指代，各材料对应的掺入量m则可在掺入的氧化物选定后通过相应的公式计算得出。

根据第4节的分析可知，为更好地优化波导的WPD，掺入氧化物A 和氧化物B 后需要将d为1～5µm范围内的阵列波导包层的热膨胀系数αClad增至2.42×10−6/℃，并维持包层的折射率nClad不变，即nClad=1.444 1(见表3中SiO2包层折射率)。因此，根据设计要求，可以由式(5)，(6)和(7)计算氧化物A和氧化物B 及沉积包层的掺入量mA，mB和mClad。其中，式(5)表达的是包层的热膨胀系数增至2.42×10−6/℃时应满足的条件，式(6)是在满足式(5)的情况下维持包层折射率为nClad=1.444 1 时应满足的条件。式(7)是体积计算公式，为近似公式，其中V是需增加热膨胀系数的包层体积，可通过前面的结构设计进行计算。

表3 包层及掺杂氧化物属性Table 3 Properties of clad and doped oxides

本文中，通过掺入P2O5和B2O3这2种氧化物来增加包层的热膨胀系数。在工艺腔中充入SiCl4，BCl3和POCl3等混合气体，采用火焰水解法(FHD)在波导上沉积掺杂包层，反应方程式如式(8)，(9)和(10)所示。参考式(5)，(6)和(7)计算掺入量，可通过在工艺腔中控制反应气体的流量来实现包层的沉积与掺杂，从而达到增加包层热膨胀系数的目的。

5.2 AWG制备工艺流程

在传统的AWG制备工艺流程中，基于等离子体干法刻蚀出光波导结构，然后通过等离子体增强化学气相沉积(PECVD)技术沉积包层即可完成基本工艺，而在本文中，则需要在AWG的不同波导部位沉积热膨胀系数不同的包层，这需要对传统工艺进行一些调整与改进，以便制备出本文所设计的AWG，优化工艺如图9所示。

在图9所示工艺流程中，通过等离子干法刻蚀出光波导后(图9(a))，采用FHD 对整个AWG 沉积掺杂包层(图9(b))，以增加包层的热膨胀系数，然后对包层表面旋涂光刻胶(图9(c))，然后光刻显影(图9(d))，暴露出不需要增加热膨胀系数的包层部位，采用感应耦合等离子体(ICP)对暴露出来的掺杂包层进行刻蚀(图9(e))，利用去胶溶剂(丙酮溶液)去除光刻胶(图9(f))，再利用FHD 对整个AWG沉积未掺杂的包层(图9(g))，最后采用化学机械抛光(CMP)对AWG表面进行均匀化处理(图9(h))，最终得到在所需波导部位沉积掺杂包层的AWG器件。

图9 AWG的制备工艺流程Fig.9 Preparation processes of AWG

6 结论

1)在石英基二氧化硅AWG中，波导间距过小会增大AWG的WPD，当波导间距为1µm时，WPD≥0.16 nm。随着波导间距增大，WPD逐渐减小。

2)通过掺杂氧化物，将与平板波导连接处波导间距为1～5 µm 的阵列波导热膨胀系数增大至2.42×10−6/℃，可将此处波导的WPD降至0.05 nm 以内。对于波导间距大于5µm 的其他部位，由于石英衬底和未掺杂的二氧化硅包层的热膨胀系数相同，可将波导的WPD降至0.05 nm 以内，从而使整个AWG器件的WPD能优化到0.05 nm以内。

3)分析掺入不同氧化物的搭配比例，并给出掺入量的计算公式，可为工艺中的掺杂提供参考，并在保证包层折射率不变的情况下增加连接处包层的热膨胀系数。

4)提出一种新工艺流程来实现在AWG器件中不同部位波导处包层的掺杂，从而制备出低WPD的AWG 器件。结合本研究给出的优化方案和工艺流程，可制备出WPD在0.05 nm以内的AWG器件，满足设计要求。