耦合激励下的弛张筛面的动力学特性
2022-01-26陈宝兴徐宁宁林冬冬王新文
陈宝兴,徐宁宁,林冬冬,王新文
(中国矿业大学(北京)化学与环境工程学院,北京,100083)
在选煤领域,黏湿物料和细物料的干法筛分是一个亟待解决的问题。传统振动筛在处理黏湿物料时效率低,且筛孔易被堵[1−4]。近年来,一些新的高效筛分设备不断问世。其中,弛张筛具有筛面加速度大,筛分效率高,适应性强和地基动载荷小等优点[5−8],得到了广泛应用。弛张筛的最大优势在于柔性筛面在激振力的作用下会产生高频、大振幅振动[9−11]。因此,研究筛面振动的动力学特性可以加深对弛张筛工作原理的认识,更好地使用与改进弛张筛。
到目前为止,前人针对筛面振动提出的理论主要基于以下3种模型:悬链线模型、简支梁模型和弹性压杆模型。XIONG 等[12]建立了基于悬链线理论的数学模型来描述筛面振动,并研究了激振器的旋转速度、筛面倾斜角和张紧量对筛面振动的影响。悬链线模型可以描述弛张筛面的静止状态,但不能描述动态过程。邹梦麒等[13]提出了1种由三段圆弧组成的张弛筛筛面模型,分析张紧量对位移、速度、加速度和等效应力的影响。ZHANG 等[14]将筛面简化为两端可以移动的简支梁模型并建立动力学方程,研究了筛面中点处的运动规律和筛上颗粒运动轨迹。对于弹性压杆模型,ZHAO等[15]将筛面视为两端可移动的弹性压杆以建立动力学模型,计算得到了加速度表达式和数值解。无论是简支梁模型还是弹性压杆模型,都认为筛面长度保持不变,这忽略了柔性筛面在振动过程中不断地拉伸和收缩的过程。
除了理论研究,也有很多关于筛面振动的实验与模拟研究。PENG等[16]通过实验研究了初始张紧量、聚氨酯筛板硬度以及驱动电机转速等因素对筛面运动特性的影响。WU 等[17]提出了一种DEM-MBD(离散元法−多刚体动力学)双向耦合方法,使用分段线性插值的方法简化了柔性筛面。ZHAO等[18]通过正交试验研究了振动参数对圆振动筛的综合影响。
尽管已经提出了许多模型来研究弛张筛面的振动,但是这些模型都忽略了筛面的纵向振动,同时,这些研究默认弛张筛面两端只受到相对纵向激励,而不讨论横向激励对筛面振动的影响。为此,本文作者提出一种基于弦振动模型和Hamilton原理的方法,分析筛面的动力学特性,可以获得筛面上任何时间和任意位置处的纵向和横向位移。
1 弛张筛简介
弛张筛的工作原理如下:柔性筛面两端分别与不同的筛框相连,筛框之间的相对运动使筛面振动。常见的弛张筛可以分为2类:
1)LIWELL式弛张筛。电机产生的扭矩通过皮带传送到曲柄连杆机构,连杆与外筛框相连。运行时,内外筛框之间有沿筛面方向的相对振动。
2)振动式弛张筛。图1所示为圆振动弛张筛。在运行时,激振器使主浮筛框做圆振动,主浮筛框之间会产生相对运动[19]。主浮筛框之间用剪切弹簧连接,剪切弹簧在水平方向刚度较小而在竖直方向刚度较大,因此,武继达等[20]认为主浮筛框之间只存在沿筛面方向的相对振动,而不存在垂直于筛面方向的相对振动。由于事实存在垂直于筛面方向的相对振动,本文在不忽略其影响的情况下,建立受横向−纵向耦合激励作用的筛面的振动方程,并求得数值解。

图1 圆振动弛张筛Fig.1 Circular vibration flip-flow screen
2 弦模型建立
图2所示为弦模型示意图。将弛张筛面中线处简化为一根弦,将两端的相对位移简化为一端固定,一端受到纵向−横向耦合激励。以水平方向为x方向,以竖直方向为y方向。弦一开始处于刚好张紧状态,弦长为l,x为初始状态时弦上固定点的横坐标(或沿弦方向的广义坐标),x∈[0,l]。弦在运动过程中既考虑纵向振动又考虑横向振动。纵向振动方向为x方向,横向振动方向为y方向。

图2 弦模型示意图Fig.2 Schematic diagram of string model
本模型基于以下2个假设:
1)弦具有连续性和均匀性,即弦的密度、弹性模量、截面积在运动过程中始终不变;
2)在每1个时刻外界激励传递的能量与筛面阻尼消耗的能量相同。
弦的纵向位移表达为u(x,t),横向位移表达为w(x,t)。将弦一端受到的耦合位移激励分解为水平方向和竖直方向的周期位移激励,因此,弦的边界条件可以表示为
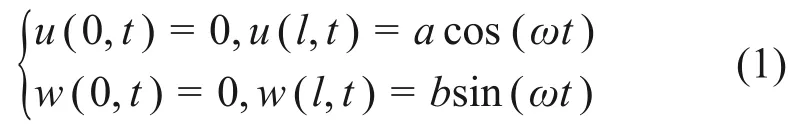
式中:a为纵向位移激励的幅值;b为横向位移激励的幅值;ω为激励的频率。
因为弦的边界条件是非齐次的,需要将其转化为齐次边界条件以方便后续的计算,将u(x,t)和w(x,t)表示为

式中:s(x,t)与g(x,t)为齐次边界条件;f(x,t)与v(x,t)为非齐次边界条件,可以表示为

它们的偏微分可以表示为

3 振动方程的建立
对于弦上任意一点任意时刻的运动,矢径r为

其中:i和j为单位向量。
速度v为

系统动能T可以表示为
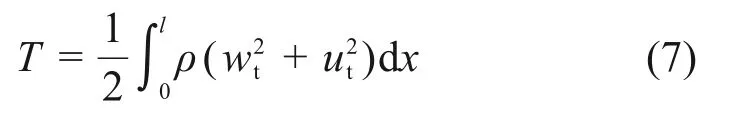
式中:ρ为弦的线密度。
系统势能V可以表示为

式中:E为弹性模量;A为弦的截面积;F0为弦初始张紧力。ε为应变,计算如下
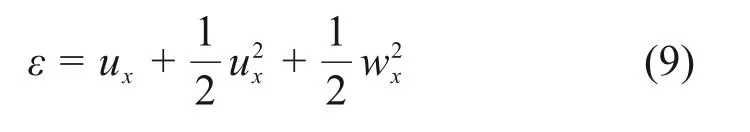
拉格朗日量L为

利用哈密顿原理:

将式(10)代入式(11)中,利用变分原理与分部积分的方法,得

将式(2)代入式(12)中,得

由于偏微分方程的求解比较困难,本文运用伽辽金法将偏微分方程转化为常微分方程。根据伽辽金法[21],g(x,t)和s(x,t)可以表示为

g(x,t)的偏微分可以表示为

s(x,t)的偏微分可以表示为

在满足边界条件的情况下,设试函数ϕi(x)为

将式(3),(4),(14)~(17)代入式(13),并在式两端同乘以权函数,得
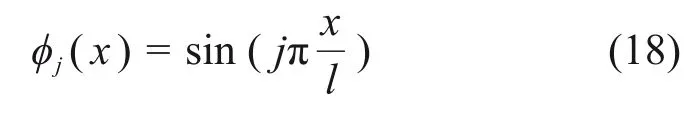
为了简化运算,定义新变量ξ,将筛面上点的位置归一化,表示为

等式两端对ξ从0 到1 积分,即可将偏微分方程转化为常微分方程,可以表示为

其中:
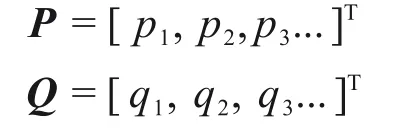
矩阵M,K1,K2,K3,K4,K5,K6,K7,K8,K9,K10,K11,F1,F2的表达式如下。
令I=iπξ;J=jπξ;N=ωt


4 模拟模型的建立
利用ABAQUS 建立筛面的仿真模型,模拟筛面的振动过程,如图3所示。在该模型中,筛面长度l为316 mm,宽d为500 mm,厚h为4 mm。筛面材料为聚氨酯,密度ρv为1 500 kg/m3。外加纵向激励的振幅a为6 mm,频率ω为10 Hz。

图3 筛面模型Fig.3 Screen panel model
由于聚氨酯材料具有超弹性,本文选择用Mooney-Rivlin 本构模型描述材料特性[20]。在两参数的Mooney-Rivlin 模型中,需要通过近似计算来获得C01和C10这2 个参数,即弹性模量E与剪切模量G近似有:E≈3G。常数C01和C10近似有:C01≈4C10,同时G=2(C01+C10)。令E=1.2 MPa 时,可以计算出C01=0.16 MPa,C10=0.04 MPa。
在ABAQUS后处理模块中,输出筛面中线处x坐标为0,39.5,79.0,118.5,158.0,197.5,237.0,276.5 和316.0 mm 的9 个点的x方向和y方向的位移。
5 理论验证
在筛面一端施加圆位移激励的情况下(即a=b),利用弦振动模型理论计算的结果与模拟结果对比,验证理论的正确性。由于筛面模型的厚度为4 mm,因此选择弦振动模型的横截面的长×宽为4 mm×4 mm,各参数取值见表1。

表1 弦振动方程中各参数取值Table 1 Value of each parameter in string vibration equation
1)将表1中各参数代入矩阵,并选取i=2,即可得到各矩阵的只含有变量t的表达式。
2)再将这些矩阵代入到式(20)中,利用MATLAB 中的四阶龙格库塔算法即可得到p(t)和q(t)的数值解。
3)在得到数值解后代入不同x即可得到筛面中线处不同位置的纵向位移和横向位移。
5.1 筛面中线处的纵向位移
选取模拟与计算结果中稳定振动1 s 结果,计算平均振幅与平均周期,部分点的结果见表2。考虑到x为0 mm和316 mm处计算结果与模拟结果是完全相同的,可得幅值的平均相对误差为9.584%,周期的平均相对误差为0.680%。
同时,绘制各点处的位移−时间图,以便直观了解理论计算与模拟结果的拟合程度。x为79,158和237 mm的3点处的位移−时间图见图4。
由表2和图4可知:理论计算与模拟结果中,纵向运动均为近似周期振动,周期约为0.1 s,这与外加激励的振动周期一致。振幅的变化规律是越靠近筛面固定端幅值越小,反之则越大。从模拟结果分析,越靠近固定端振动的稳定性越差,振幅变化越大。利用MATLAB 对结果进行快速傅里叶变换,得到的筛面中点处的幅频曲线,如图5所示。

表2 纵向振动的模拟与计算结果对比Table 2 Comparison of simulation and calculation results of axial vibration

图4 纵向振动的时间−位移图Fig.4 Time domain diagrams for axial displacement
由图5可知:在计算结果中,振幅最大时对应的频率为10 Hz,在模拟结果中也是10 Hz,这与外加激励的频率相同。在其他频率处的振幅很小。在计算结果中最大振幅为3.036 mm,模拟结果中最大振幅为3.212 mm,相对误差为5.48%。
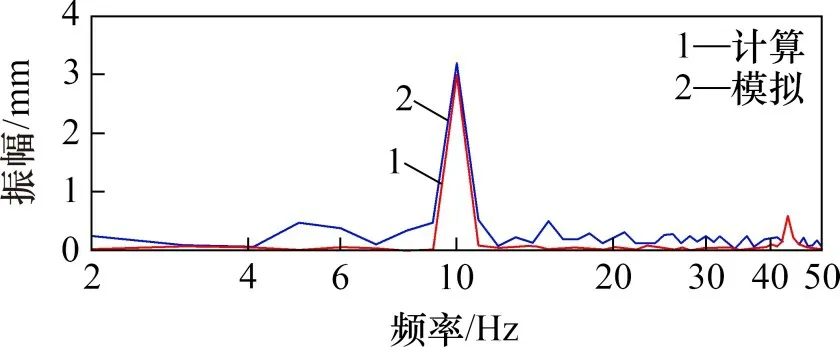
图5 纵向振动的幅频特性曲线Fig.5 Frequency domain characteristics for axial displacement
5.2 筛面中线处的横向位移
与5.1节相同,选取模拟与数值计算结果中的稳定振动1 s 结果,将各点处的横向振动的平均振幅和平均周期列于表3中。考虑到x为0 mm和316 mm处计算结果与模拟结果完全相同,幅值的平均相对误差为7.017%,周期的平均相对误差为1.157%。
x分别为79,158 和237 mm 时3 点的时间−位移图见图6。
由表3和图6可知:在理论计算与模拟结果中,横向运动与纵向运动都为近似周期振动,周期均与外界激励振动周期一致。横向振动振幅的变化规律是越靠近筛面中点处振幅越大,反之则越小。

图6 横向振动的时间−位移图Fig.6 Time domain diagrams for lateral displacement

表3 横向振动的模拟与计算结果对比Table 3 Comparison of simulation and calculation results of lateral vibration
利用MATLAB 对结果进行快速傅里叶变换,得到的筛面中点处的幅频曲线见图7。

图7 横向振动的幅频特性曲线Fig.7 Frequency domain characteristics for the lateral displacement
与5.1节纵向振动一样,横向振动的计算结果与模拟结果中振幅最大时对应的频率均为10 Hz。在其他频率处的振幅相对而言很小。在计算结果中最大振幅为36.68 mm,模拟结果中最大振幅为39.67 mm,相对误差为7.54%。
理论计算与模拟结果之间存在偏差,分析可能的原因:
1)本文假设筛面在任意时刻由阻尼消耗的能量与外界激励输入的能量相等,事实上在稳定振动的状态下,一个振动周期内遵循这个规则,而每个时刻下输入的能量与消耗的能量并不完全相等;
2)为简化计算,本文假设弹性模量始终保持不变,而利用本构模型描述的聚氨酯材料的超弹性,应力与应变之间的关系是非线性的,这也影响了计算结果的准确性。
6 横向激励的影响
在研究筛面振动时,最值得关注是筛面的横向振动,因此,分析不同横向激励对筛面的横向振动的影响。在保持纵向激励不变的情况下,分别计算横向激励振幅b=0,2和4 mm时筛面中点处的横向位移,与b=6 mm时的筛面中点处的横向位移进行比较。选取筛面中点稳定振动1 s 结果,横向振动的位移−时间图见图8。
由图8可知:在不同横向激励的作用下,筛面仍然在进行近似周期振动,但横向振动的振幅与周期都发生了变化。b从0 mm增大到6 mm,对应的平均振幅从27.43 mm 增大到54.25 mm,对应的平均周期从0.21 s 减小到0.10 s。在完全没有横向激励的情况下,筛面的横向振动周期为0.21 s,约为外加纵向激励周期的2 倍,而随着横向激励增强,筛面的横向振动周期越来越接近于纵向−横向耦合激励的周期。此外,由于振幅及振动频率增大,筛面的速度与加速度增幅更明显。尤其是被认为对筛分效率影响最大的筛面加速度,通过计算,横向激励幅值b从0 mm增大到6 mm,对应的筛面中点的最大加速度从10.3g增大到43.6g。加速度的大幅增加将有利于物料的深度筛分。周期、振幅和加速度的变化如图9所示。

图8 不同振幅的横向激励作用下筛面中点横向振动的位移−时间图Fig.8 Time domain diagrams at midline of panel for lateral vibration with different excitations

图9 不同幅值的横向激励作用下振动的周期、振幅和加速度图Fig.9 Period,amplitude and acceleration of lateral vibration with different lateral excitations
本文提出的新的弦振动的优点有:
1)弦在振动过程中的张紧松弛运动与弛张筛的弛张运动更吻合,并且可以得到每个时刻每个位置处的动力学参数。
2)考虑了弛张筛筛板受到纵向−横向耦合激励时的运动,更符合弛张筛筛板的实际运动情况。
在工程实践中,往往通过增加或减少剪切弹簧来调节主浮筛框之间的沿筛面方向的刚度,这一过程中垂直于筛面方向的刚度变化往往被忽略,本文证明这种变化对弛张筛筛面振动有一定的影响。
7 结论
1)提出一种基于弦振动模型和Hamilton 原理的筛面振动理论。筛面在耦合激励作用下在纵向与横向上分别进行近似周期振动。对于纵向振动,计算结果与模拟结果相比,幅值平均相对误差为9.584%,周期平均相对误差为0.680%;对于横向振动,幅值平均相对误差为7.017%,周期平均相对误差为1.157%。
2)随着横向激励振幅增大,筛面中点处横向振动的幅值由27.43 mm 增大54.25 mm,振动周期由0.21 s 减小到了0.1 s,加速度则由10.3g增加到了43.6g,说明让筛面两端存在适当横向相对运动有助于增强筛面振动强度,进而提高弛张筛的筛分效率。
3)本文为了简化计算而假设筛面在任意时刻由阻尼消耗的能量与外界激励输入的能量相等以及弹性模量始终保持不变,在一定程度上影响了计算结果的准确性,在后续研究中将改进这2点。
